10.2: Linealización de ODEs
- Page ID
- 85554
Introducción
Los procesos de ingeniería química a menudo operan de manera no lineal e inestable (es decir, no siempre en estado estacionario), y generalmente se rigen por ecuaciones diferenciales ordinarias (ODEs) no lineales. La ODE es una relación que contiene funciones de una sola variable independiente y derivadas con respecto a esa variable. Muchos estudios se han dedicado a desarrollar soluciones a estas ecuaciones, y en los casos en que la ODE es lineal se puede resolver fácilmente usando un método analítico. Sin embargo, si la ODE es no lineal y no todos los parámetros operativos están disponibles, frecuentemente es difícil o imposible resolver ecuaciones directamente. Incluso cuando se conocen todos los parámetros, se necesitan poderosas herramientas computacionales y matemáticas para resolver completamente las ODE con el fin de modelar el proceso. Para simplificar este procedimiento de modelado y obtener funciones aproximadas para describir el proceso, los ingenieros suelen linealizar las ODEs y emplean matemáticas matriciales para resolver las ecuaciones linealizadas.
Una ecuación lineal es una ecuación en la que cada término es una constante o el producto de una constante multiplicada por la primera potencia de una variable. Estas ecuaciones se denominan “lineales” porque representan líneas rectas en coordenadas cartesianas. Una forma común de una ecuación lineal en las dos variables\(x\) y\(y\) es\(y = mx + b\). Esto se opone a una ecuación no lineal, como
\[m = e^x + x^2 + 2x + 5. \nonumber \]
A pesar de\(2x + 5\) que es una porción lineal de la ecuación,\(e^x\) y no lo\(x^2\) son. Cualquier término no lineal en una ecuación hace que todo el sistema no sea lineal.
Sistema no lineal de ecuaciones:
\ [\ begin {alinear*}
\ dfrac {d A} {d t} &=3 A^ {2} +2 B+C-7 D^ {3}\\ [4pt]
\ dfrac {d B} {d t} &=A+C^ {2} +2 D\\ [4pt]
\ dfrac {d C} {d t} &=A+4 B^ {2} ^ {2}\\ [4pt]
\ dfrac {d D} {d t} &=2 C-D\ final {alinear*}\ nonumber\]
Después de la linealización (alrededor del punto de estado estacionario {-0.47, -0.35,0.11,0.23}:
\ [\ left (\ begin {array} {c}
A^ {\ prime}\
B^ {\ prime}\
C^ {\ prime}\
D^ {\ prime}\ end {array}
\ derecha) =\ left (\ begin {array} {cccc}
-2.83 & 2 & 1 & 0\\ 1 & 0\\
1 & 0 & 0.23 & 0\\
1 & ; -2.78 & -0.23 & 0\\
0 & 0 & 2 & 0
\ end {array}\ derecha)\ left (\ begin {array} {c}
A\\
B\\
C\
D
\ end {array}\ derecha) +\ left (\ begin {array} {c}
k_ {1}\\
k_ {2} \\
k_ {3}\\
k_ {4}
\ end {array}\ derecha)\ nonumber\]
Obsérvese que cada ecuación está compuesta únicamente por variables de primer orden.
Aunque es poco probable que el proceso de ingeniería química a modelar opere de manera lineal, todos los sistemas pueden aproximarse como lineales en un punto. Esto se prefiere ya que los sistemas lineales son mucho más fáciles de trabajar que las ecuaciones no lineales. Aunque la linealización no es una solución exacta a las ODEs, sí permite a los ingenieros observar el comportamiento de un proceso. Por ejemplo, las ODE linealizadas se utilizan a menudo para indicar exactamente qué tan lejos del estado estacionario se desvía un proceso dado sobre rangos de operación especificados. Esta página wiki analiza cómo resolver una ODE linealizada a mano y usando Mathematica, y procede a elaborar varios ejemplos de ODEs linealizados comúnmente vistos en la práctica de ingeniería química.
Aplicaciones a la Ingeniería Química
Como se mencionó anteriormente, la linealización de ODEs permite a los ingenieros comprender el comportamiento de su sistema en un punto dado. Esto es muy importante porque muchas ODEs son imposibles de resolver analíticamente. También conducirá a determinar la estabilidad local de ese punto. La mayoría de las veces un sistema se linealizará en torno al estado estacionario, pero no siempre es así. Te puede interesar entender el comportamiento de tu sistema en su punto de funcionamiento o estado de equilibrio (no necesariamente estado estacionario). El enfoque de linealización puede ser utilizado para cualquier tipo de sistema no lineal; sin embargo, como ingeniero químico, la linealización generalmente involucrará ODEs. Los ingenieros químicos utilizan ODEs en aplicaciones como CSTR, intercambiadores de calor o crecimiento celular biológico.
También es importante entender las ventajas y desventajas de linealizar un sistema de ODEs:
Ventajas
- Proporciona una manera más simple y conveniente de resolver las ODEs
- Se puede observar el comportamiento de un proceso
- Se puede utilizar cualquier tipo u orden de ODE
Desventajas
- La solución es solo una solución exacta en el punto elegido; de lo contrario, es una aproximación y se vuelve menos precisa lejos del punto
- Aunque la linealización es una alternativa más rápida, lleva tiempo aprender inicialmente el proceso (por ejemplo, usando Mathematica)
Otro uso para la linealización de las ecuaciones que rigen los procesos químicos es determinar la estabilidad y características de los estados estables. Para ello se pueden usar sistemas de ODEs linealizados, y los métodos para hacerlo se pueden encontrar en Puntos Fijos, Autovectores y Valores propios, y Usar valores propios y vectores propios para encontrar estabilidad y resolver ODEs
Procedimiento General de Linealización
La linealización es el proceso en el que un sistema no lineal se convierte en un sistema lineal más simple. Esto se realiza debido al hecho de que los sistemas lineales suelen ser más fáciles de trabajar que los sistemas no lineales. Para este curso, el proceso de linealización se puede realizar utilizando Mathematica. Las instrucciones específicas sobre cómo hacer esto se pueden encontrar a continuación.
- Elija un punto relevante para la aproximación lineal, dos opciones disponibles son:
- Estado estacionario: puntos donde el sistema no cambia
- Ubicación actual- dado donde se encuentra ahora
- Calcular la matriz jacobiana en ese punto. El jacobiano es esencialmente una expansión de la serie Taylor.
- Resuelve encontrar constantes desconocidas usando métodos algebraicos.
Linealización a Mano
Para linealizar una ecuación diferencial ordinaria (ODE), se puede emplear el siguiente procedimiento. Se utiliza una ecuación diferencial simple para demostrar cómo implementar este procedimiento, pero cabe señalar que cualquier tipo u orden de ODE puede linealizarse utilizando este procedimiento.
1. Use una expansión de la serie Taylor (truncando después de los términos lineales) para aproximarse al lado derecho de la ODE.
Digamos que comenzamos con la siguiente ODE:
\[\frac{d x}{d t}=f(x)=3 x^{2}.\nonumber \]
Esta ODE describe el comportamiento de alguna variable,\(x\), con respecto al tiempo.
Una serie Taylor es una expansión en serie de una función alrededor de un punto. Si\(x= a\), una expansión de una función real viene dada por:
\[f(x)=\sum_{n=0}^{\infty} \frac{f^{n}(a)}{n !}(x-a)^{n}\nonumber \]
\[f(x) = f(a)+f^{\prime}(a)(x-a)+\frac{f^{2}(a)}{2 !}(x-a)^{2}+\frac{f^{3}(a)}{3 !}(x-a)^{3}-\ldots+\frac{f^{n}(a)}{n !}(x-a)^{n}+\ldots\nonumber \]
Cuando\(x=0\), la función también se conoce como serie Maclaurin. El teorema de Taylor afirma que cualquier función que satisfaga ciertas condiciones puede expresarse como una serie de Taylor.
En aras de la simplicidad, solo los dos primeros términos (los términos cero y de primer orden) de esta serie se utilizan en las aproximaciones de Taylor para linealizar ODEs. Adicionalmente, este truncamiento (es decir. “cortar” los términos\(n=2\) y términos superiores del polinomio mostrado anteriormente) asegura que la Serie Taylor es un polinomio lineal. Si se usan más términos, el polinomio tendría\((x − a)^2\) y términos de orden superior y se convertiría en una ecuación no lineal. La variable '\(a\)' en la serie Taylor es el punto elegido para linealizar la función alrededor. Debido a que se desea que la mayoría de los procesos funcionen en estado estacionario, este punto será el punto de estado estacionario. Entonces, nuestra ecuación diferencial se puede aproximar como:
\[\frac{d x}{d t}=f(x) \approx f(a)+f^{\prime}(a)(x-a)=f(a)+6 a(x-a)\nonumber \]
Dado que\(a\) es nuestro punto de estado estacionario, siempre\(f(a)\) debe ser igual a cero, y esto simplifica nuestra expresión más abajo a:
\[\frac{d x}{d t}=f(x) \approx f^{\prime}(a)(x-a)=6 a(x-a)\nonumber \]
El gráfico que se muestra arriba muestra la aproximación de f (x) a (x, f (x)). Como se mencionó anteriormente, la linealización es solo una aproximación para cualquier función dada cerca de un punto continuo. Cuando se trabaja con un sistema de ODEs, el jacobiano se escribe como una matriz. Es la matriz de constantes necesarias para describir la linealidad de un sistema. Se puede pensar en el jacobiano como cuánto se distorsiona un sistema para adquirir una identidad lineal. Una matriz jacobiana siempre será un cuadrado (#rows = #columns) y muestra cómo varía cada ecuación con cada variable. La matriz jacobiana se define como:
\ [J\ izquierda (x_ {1},\ ldots, x_ {n}\ derecha) =\ izquierda [\ begin {array} {ccc}
\ frac {\ parcial y_ {1}} {\ parcial x_ {1}} &\ cdots &\ frac {\ parcial y_ {1}} {\ parcial x_ {n}}\
\ vdots &\ ddots &\ vdots\\
\ frac {\ parcial y_ {n}} {\ parcial x_ {1}} &\ cdots &\ frac {\ parcial y _ {n}} {\ parcial x_ {n}}
\ end {array}\ derecha]\ nonumber\]
Y se usa como tal para este conjunto no lineal de ecuaciones
\ [\ begin {array} {l}
\ frac {d x} {d t} =2 x^ {2} +\ cos (5 y) -12\ arctan (z-3)\
\ frac {d y} {d t} =7 y^ {3} +\ sin (5 x)\
\ frac {d z} {d t} =1.3\ log (x+y)
\ fin {matriz}\ nonumber\]
El sistema linealizado es
\ [\ left [\ begin {array} {l}
x^ {\ prime}\
y^ {\ prime}\
z^ {\ prime}
\ end {array}\ right] =\ left [\ begin {array} {lll}
J_ {1} & J_ {2} & J_ {3}\\
J_ {4} & J_ {5} & J_ {6}\\
J_ {7} y J_ {8} y J_ {9}
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
y\\
z
\ end {array}\ right] +\ left [\ begin {array} {l}
c_ {1}\\
c_ {2}\\
c_ {3}
\ end {array}\ right]\ nonumber\]
La matriz cuadrada es la jacobiana.
Digamos que tienes el siguiente conjunto de ecuaciones y quieres encontrar su matriz jacobiana alrededor del punto\ (A=3,\, B=2).
\[\frac{d A}{d t}=3 A-A^{2}-A B\nonumber \]
\[\frac{d B}{d t}=6 B-A B-2 B^{2}\nonumber \]
Encontramos al jacobiano tomando la derivada de cada ecuación con respecto a cada variable.
\[\frac{d\left(3 A-A^{2}-A B\right)}{d A}=3-2 A-B\nonumber \]
\[\frac{d\left(3 A-A^{2}-A B\right)}{d B}=-A\nonumber \]
\[\frac{d\left(6 B-A B-2 B^{2}\right)}{d A}=-B\nonumber \]
\[\frac{d\left(6 B-A B-2 B^{2}\right)}{d B}=6-A-4 B\nonumber \]
Estas son las ecuaciones en la matriz. Los valores de las variables desde cualquier punto que estemos linealizando se ponen luego en estas ecuaciones y se calculan para obtener el jacobiano.
\ [J a c=\ left [\ begin {array} {cc}
3-2 A-B & -A\\
-B & 6-A-4 B
\ end {array}\ right] A=4, B=2\ nonumber\]
\ [J a c=\ left [\ begin {array} {ll}
-7 & -4\\
-2 & -6
\ end {array}\ right]\ nonumber\]
2. Cambiar la aproximación linealizando alrededor de un punto de estado estacionario para describir cómo el proceso se desvía del estado estacionario.
Se puede hacer la siguiente sustitución:
\[\frac{d x}{d t}=\frac{d(x-a)}{d t}\nonumber \]
\[\frac{d(x-a)}{d t} \approx 6 a(x-a)\nonumber \]
Esta sustitución está permitida porque 'a' es una constante, y la derivada de una constante es cero.
Sustituir (x-a) por x significa que nuestra ecuación diferencial ahora muestra cómo nuestra función, x, se desvía del valor de estado estacionario, a, con respecto al tiempo. Esta desviación, (x-a), se expresa comúnmente como x ′. También hay que señalar que la cantidad '6a' es una constante, y así se reconocerá además como 'A'.
Nuestra ecuación linealizada final se convierte en:
\[\frac{d x^{\prime}}{d t} \approx A x^{\prime}\nonumber \]
La ODE una vez no lineal,
\[\frac{d x}{d t}=f(x)=3 x^{2}\nonumber \]
ahora se ha simplificado en una ecuación diferencial lineal.
El procedimiento de linealización suele ocurrir alrededor del punto o puntos de estado estacionario de un proceso especificado. Los ingenieros anticipan un cierto cambio en la salida para el punto de estado estacionario particular, y pueden proceder a linealizar a su alrededor para completar su aproximación. Por favor, siga el gráfico a continuación para obtener más detalles. Tenga en cuenta que se produce un punto de estado estacionario cuando\(dx / dt = 0\)
\[\rror Plot Color New 1.jpg\nonumber \]
Como se puede ver, alejarse más del punto de estado estacionario da como resultado una desviación significativamente mayor y, por lo tanto, un error (linealización real).
Ocasionalmente, para condiciones de operación muy únicas, la gerencia de la planta puede decidir ejecutar momentáneamente un proceso fuera de condiciones estrictas de estado estacionario (tal vez un procedimiento único de arranque, recuperación de cierre, etc.). Para reforzar el concepto de linealización en torno a un punto de estado inestable (elegido arbitrariamente en este ejemplo), considere la siguiente representación visual. Obsérvese que a=50 y C=7500 en la primera parcela.
\[\ew Image 2.jpg\nonumber \]
La segunda parcela es una ampliación de una pequeña sección de la primera parcela. Como uno puede notar fácilmente, tanto la aproximación lineal como la gráfica real se superponen casi exactamente en este pequeño rango. Esto ilustra cómo esta linealización particular podría ser utilizada para aproximar esta región de la función y puede describir su comportamiento con bastante precisión. Esta técnica de aproximación utilizando la linealización de ODE se puede realizar alrededor de diferentes puntos (diferentes valores de a) utilizando el mismo método para modelar el comportamiento del resto de la función dx/dt vs x. Nota: el recálculo frecuente de la constante de integración, C, permite una mayor precisión en la aproximación.
Ejemplo de un proceso de linealización simple en uso
Siempre que sea una circunstancia en la que el desarrollo de una solución analítica rigurosa sea inviable debido al tiempo, el acceso a los recursos informáticos o la capacidad matemática, el proceso de linealización ofrece una alternativa conveniente y rápida.
Una introducción apropiada a la aplicación de linealización se presenta en la sección 5.3 de la lectura de Bequette y se describe a continuación.
El siguiente modelo describe el comportamiento de la altura del tanque en función del tiempo (t), frente a un caudal de líquido entrante en estado estacionario. dh/dt representa el cambio en la altura del fluido contenido dentro del tanque en función del tiempo, h indica la altura (o nivel) o el fluido contenido dentro del tanque, F representa la magnitud del flujo entrante. El siguiente modelo describe la fluctuación nivel/altura del tanque como función tanto de la altura actual (h) como del flujo (F). El fluido ingresa al tanque como flujo por área de entrada (F/A), y sale en función de un término proporcional correctivo, β, también por área de salida, multiplicado por la raíz cuadrada de la altura actual.
En lugar de que el fluido salga a través de este término, también podemos considerarlo una forma de control de retroalimentación, que posteriormente reduce la cantidad de fluido de entrada en su lugar (depende de la aplicación, el resultado final es idéntico). Por lo tanto:
\[\frac{d h}{d t}=f(h, F)=\frac{F}{A}-\frac{\beta}{A} * \sqrt{h} \nonumber \]
Nota importante sobre la relevancia de las variables proporcionadas:
F s indica el caudal inicial para el sistema descrito y es importante para calcular la intercepción y posteriormente el término correctivo calculativo para la linealización (si la linealización no se realiza en estado estacionario, como en este ejemplo). h s describe la altura del tanque para el caudal especificado, F s. Al conectar el valor de h s a la fórmula linealizada, notará que f (h, F s) = 0, el punto en la gráfica donde coinciden tanto la linealización como la ecuación característica (es decir, son tangentes).
h sigue siendo una variable para la derivación para que los estudiantes puedan notar que es una variable dependiente (dependiente del caudal). Bequette debe (y hace) proporcionar tanto los valores para F s, h s para que pueda continuar una linealización (de lo contrario simplemente tendremos una ecuación que describa la pendiente sin punto característico por el que pasar).
Parámetros del sistema (F s es un ejemplo de caudal en estado estacionario, esta información se utiliza para determinar la intercepción de la fórmula linealizada):
\[A=1 f t^{2} ; h_{s}=5 f t ; \beta=\frac{1}{\sqrt{5}} \frac{f t^{2.5}}{m i n} ; F_{s}=\frac{1 f t^{3}}{m i n} \nonumber \]
Reescribiendo el sistema con las variables de entrada:
\[\frac{d h}{d t}=f\left(h, F_{s}\right)=1+\frac{1}{\sqrt{5}} * \sqrt{h} \nonumber \]
Para linealizar alrededor de un cierto punto, simplemente evalúe la derivada de la función deseada y agregue una constante correctiva, C, representada por el valor de la función en la condición inicial (especificada).
\[\(h,F_s) \approx f(h,F_s)+ \frac{\partial{f}}{\partial{h}}|_h, _{F_s}(h-h_s) \nonumber \]
\[\(h,F_s) \approx 0+ \frac{-1}Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.02:_Linealización_de_ODEs), /content/body/div[5]/p[15]/span/span, line 1, column 2
Seleccionando, h=5 para linealizar alrededor, presentamos una versión adaptada del ejemplo de texto (la linealización es en rojo):
\[\(h,1) \approx 0+ \frac{-1}Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.02:_Linealización_de_ODEs), /content/body/div[5]/p[17]/span/span, line 1, column 2
\[\(5,1) \approx 0+ \frac{-1}Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.02:_Linealización_de_ODEs), /content/body/div[5]/p[18]/span/span, line 1, column 2
f (h ,1) aprox. = − 0.1 * (h − 5)
\[\isual 3.jpg \nonumber \]
El significado físico de este ejemplo:
El modelo describe una situación en la que un tanque mantiene el punto de ajuste de estado estacionario, un nivel (altura) de 5 pies, regulando los caudales de entrada (y/o salida). Una altura por encima del nivel preferido de 5 pies da como resultado un cambio negativo de altura por tiempo; a la inversa, una altura por debajo del nivel preferido de 5 pies da como resultado un cambio positivo de altura por tiempo, para acercarse siempre al nivel de estado estacionario.
Además, tenga en cuenta que el sistema linealizado responde relativamente más lento que el sistema de ecuaciones características (no lineal) cuando el nivel del tanque cae por debajo de 5 pies y más rápido que el sistema de ecuaciones características cuando el nivel del tanque está por encima de 5 pies.
Siga leyendo a continuación para aprender una técnica paso a paso sobre cómo completar este método para la mayoría de las ecuaciones.
Linealización usando Mathematica
La mayoría de las ODE no son tan simples como el ejemplo elaborado anteriormente. Para aquellos que se pueden resolver analíticamente, se puede utilizar el método 'a mano' de la sección anterior, aunque la matemática se vuelve complicada y tediosa cuando se trata de sistemas de ODEs. Para aquellos que no pueden resolverse analíticamente y sólo pueden aproximarse numéricamente, a veces es imposible hacer el análisis numérico a mano. Para estas ODEs, se pueden utilizar potentes herramientas computacionales como Mathematica para realizar linealización.
El siguiente archivo de Mathematica contiene un ejemplo elaborado (CSTR con intercambio de calor). Este ejemplo contiene múltiples ODEs y múltiples tipos de variables. Cuando se trata de ODEs, hay tres tipos principales de variables: estado, entrada y salida. Las variables de estado describen el sistema en cualquier momento dado (es decir. Ca, Cb, T, etc.). Las variables de entrada son simplemente entradas en el sistema. Las variables de salida son aquellas que no están directamente relacionadas con las entradas, sino que dependen de las variables de estado (es decir, k, la constante de reacción). Descubrirá en el ejemplo CSTR que es necesario linealizar las variables de estado y las variables de salida por separado.
Antes de continuar con el archivo de Mathematica presentaremos primero algunos de los comandos de Mathematica que serán necesarios para linealizar el ejemplo del CSTR.
Tenga en cuenta que es necesario presionar shift+enter (shift+return en Mac) después de un comando para evaluar la expresión.
Ejemplo:
En [1] = ((0.04587*54.32497+4.59058433734947^7) /48700043) ^131.94564
Fuera [1] = 0.000411241
Otra cosa a tener en cuenta es el uso de operadores de asignación e igualdad.
= se llama operador de asignación inmediata y: = se llama operador de asignación retardada. Cuando se utiliza el operador de asignación inmediata, se evalúa el lado derecho del operador cada vez que se realiza una asignación. Sin embargo, cuando se utiliza el operador de asignación retardada, el lado derecho se evalúa solo cuando se solicita el valor de la expresión en el lado izquierdo.
lhs=rhs rhs está destinado a ser el “valor final” de lhs (por ejemplo, f [x_] =1-x^2) lhs: =rhs rhs da un “comando” o “programa” para ser ejecutado cada vez que pida el valor de lhs (por ejemplo, f [x_] :=Expandir [1-x^2])
p: = x^3 - 6 x^2 + 11 x - 6
Esta entrada, que no produce salida, asigna la expresión polinómica a la variable p. La asignación se realiza porque este polinomio puede ser usado nuevamente más tarde, por lo que la asignación guarda su reescritura. El operador de igualdad ==, que se utiliza aquí para formar la ecuación que estamos pidiendo a Mathematica que resuelva:
En [2] := Resolver [p == 0]
Fuera [2] =
Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.02:_Linealización_de_ODEs), /content/body/div[6]/p[14]/span, line 1, column 4
Al resolver ODEs no lineales usando Mathematica, es necesario formar una matriz y hay varios comandos que se pueden usar para crear matrices.
D [X, Y]
Este comando toma la derivada parcial de una expresión (X) con respecto a una variable (Y) definida por el usuario. El primer término entre corchetes es la experiencia que deseas diferenciar, el segundo es la variable que deseas diferenciar con respecto a.
ApéndRows [column1, columna2]
Este comando crea una matriz mediante la combinación de dos columnas. Para poder utilizar este comando primero debes cargar el paquete de Manipulación Matrix usando el comando <<LineAlgebra`MatrixManipulation`
M = Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.02:_Linealización_de_ODEs), /content/body/div[6]/p[20]/b/span, line 1, column 3
Este comando crea una matriz, en este caso una matriz 3x3.
MatrixForm [X]
Este comando muestra una matriz especificada en forma de matriz.
Estos comandos nos permitirán continuar con la linealización del problema CSTR que se muestra a continuación. 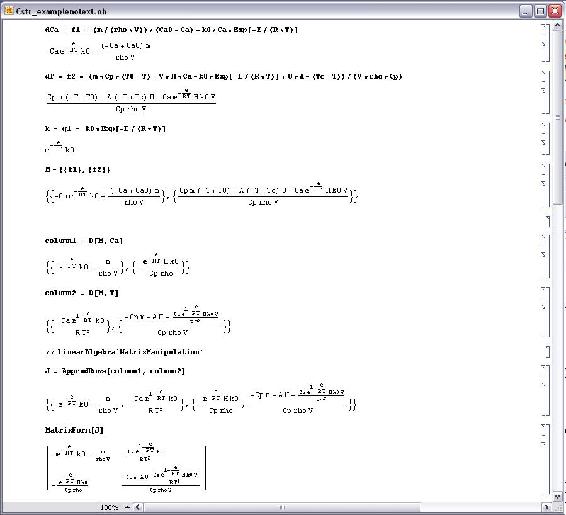
Los tres primeros comandos ingresan las ecuaciones que rigen el comportamiento de la concentración, Ca, la temperatura, T y la velocidad de reacción, k Una vez ingresadas las ecuaciones en Mathematica se crea una matriz, M, con una columna y dos filas que contienen las ecuaciones para Ca y T. A continuación se crean dos nuevas matrices tomando la derivada de la matriz M es con respecto tanto a Ca como a T. Estas matrices, llamadas column1 y column2 respectivamente, juntas forman el jacobiano del sistema y luego se muestran en forma de matriz. La matriz jacobiana es la matriz de todas las derivadas parciales de primer orden de una función valorada por vector. Su importancia radica en el hecho de que representa la mejor aproximación lineal a una función diferenciable cerca de un punto dado. Por ejemplo, dado un conjunto y=f (x) de n ecuaciones en variables x 1, x 2,... , x n, la matriz jacobiana se define de la siguiente manera:
\[\acobianmatrix.gif \nonumber \]
\[\athematicapg2.JPG \nonumber \]
Ahora que tenemos el jacobiano necesitamos crear una matriz que contenga la desviación del estado estacionario para cada una de las variables. Esta matriz, SS, contiene la concentración y temperatura reales, C y T, menos la concentración y temperatura en estado estacionario, Cas y Ts. A continuación, la matriz se muestra en forma de matriz. Ahora tenemos tanto la jacobiana como la matriz de desviación para las variables de estado. Los siguientes cuatro comandos crean la matriz jacobiana y desviación para la variable de salida, k. El primer comando crea la matriz jacobiana tomando la derivada de la ecuación k con respecto a Ca y T. El jacobiano se muestra entonces en forma de matriz. Finalmente, la matriz de desviación para k se crea de la misma manera que la anterior y luego se muestra en forma de matriz. Obsérvese que debido a que k está definido anteriormente, esta expresión se sustituye por k en la matriz de desviación. El siguiente archivo de Mathematica contiene el código que se muestra arriba con comentarios adicionales explicando por qué se realiza cada paso Media:CSTR_Ejemplo.nb. Puede ser útil bajar este archivo y ejecutar el programa en Mathematica usted mismo para tener una idea de la sintaxis. La descarga del archivo también te permitirá realizar cualquier cambio y edición para personalizar este ejemplo a otro ejemplo de interés.
Nota: Este archivo debe guardarse en su computadora y luego abrirse usando Mathematica para ejecutarse correctamente.
Para ver otro ejemplo vamos a linealizar las primeras 4 ecuaciones diferenciales dadas en la sección de introducción.
Sistema no lineal de ecuaciones:
\[\frac{dA}{dt}=3A^2+2B+C-7D^3 \nonumber \]
\[\frac{dB}{dt}=A+C^2+2D \nonumber \]
\[\frac{dC}{dt}=A+4B^2-C^2 \nonumber \]
\[\frac{dD}{dt}=2C-D \nonumber \]
Después de la linealización (alrededor del punto de estado estacionario {-0.47, -0.35,0.11,0.23}:
\ [\ left (\ begin {array} {c}
A^ {\ prime}\
B^ {\ prime}\
C^ {\ prime}\
D^ {\ prime}
\ end {array}\ derecha) =\ left (\ begin {array} {cccc}
-2.83 & 2 & 1 & -1.10\\
1 & 0 & 0.23 & 2\\
1 & -2.78 & -0.23 & 0\\
0 & 0 & 2 & -1
\ end {array}\ derecha)\ left (\ begin {array} {l}
A\\
B\\
C\
D
\ end {array}\ derecha) +\ left (\ begin {array} {c}
0.50\
0 .01\\
0.47\\
0
\ end {array}\ derecha)\ nonumber\]
Las 4 ecuaciones diferenciales anteriores se agregan a un código de Mathematica como “eqns” y “s1” son los puntos fijos de los diferenciales. Los valores de estado estacionario encontrados para “a, b, c y d” se denominan “S1DoubleBrackets (7)” Después de encontrar los valores de estado estacionario, la matriz jacobiana se puede encontrar en esos valores.
Para encontrar “k1, k2, k3 y k4” las constantes de la ecuación de la matriz de linealización, se debe definir “m1”, que es la 2da matriz en el lado derecho de la ecuación de la matriz de linealización.
Para determinar los valores k (en forma de matriz), ejecute el producto de punto de “m1" y la matriz “Jac”, lo cual es realizado por el operador “.”. Por lo tanto debería verse como “JAC.m1"
Para obtener los valores k, determinando el “JAC.m1" en los valores de estado estacionario, lo cual es realizado por el operador “/.” Por lo tanto debería verse como “JAC.m1/.S1DoubleBrackets (7)”
Digamos que tienes un sistema regido por el siguiente sistema de ecuaciones:
\[\begin{align*} \dfrac{d X_{a}}{d t} &=3 X_{a}^{2}+2 X_{b}+F_{o} \\[4pt] \dfrac{d X_{b}}{d t} &=6 X_{a}+9 X_{b}^{2}+X_{a} X_{b}+F_{o} \\[4pt] Y &=X_{a}^{2}+3 * F_{o}^{2} \end{align*} \nonumber \]
En este caso,\(X_a\) y\(X_b\) son variables de estado (describen el estado del sistema en un momento dado),\(F_o\) es una variable de entrada (ingresa al sistema y es independiente de todas las variables de estado), y\(Y\) es la salida del sistema y es dependiente tanto del estado como variables de entrada. Por favor, linealice este sistema usando Mathematica.
Utilice el archivo Mathematica presentado en el artículo para linealizar el ejemplo CSTR presentado en el modelo ODE & Excel CSTR con intercambio de calorwiki alrededor del estado estacionario (T = 368.4K y Ca = 6.3mol/L). Utilice las constantes presentadas en su ejemplo. Utilice la linealización para aproximar Ca a 369K.
Solución
La aproximación lineal da una concentración de a (Ca) de 7.13 mol/L El archivo de Mathematica utilizado para resolver este problema se puede descargar aquí. Media:linearizationexample.nb Si tiene problemas para ejecutar el archivo de Mathematica intente hacer clic derecho en el enlace y usar la opción Guardar destino como.
Ejercicio\(\PageIndex{1}\)
En una linealización de ODE, ¿en qué punto del proceso se centra generalmente la linealización?
a. Punto inicial
b. Punto final
c. Punto de estado estacionario
d. Punto medio
- Contestar
-
Respuesta: c
Ejercicio\(\PageIndex{2}\)
¿Qué hace la función D [] en Mathematica?
a. Encontrar el determinante de una matriz
b. Encuentra la derivada parcial a función o funciones
c. Encontrar el producto punto de dos matrices
d. Integrar una matriz o función
- Contestar
-
Respuesta: b
Referencias
- Bechette, B. Wayne. Dinámica de Procesos: Modelado, Análisis y Simulación. Prentice- Salón PTR, Upper Saddle River, NJ 07458 (c) 2006.
- Kravaris, Costas. Control de Procesos Químicos: Un Enfoque en el Dominio del Tiempo, Apéndice A. Departamento de Ingeniería Química, Universidad de Michigan, Ann Arbor, MI.
- Bhatti, M. Asghar. Métodos de optimización práctica con aplicaciones de Mathematica. Springer Telos.


