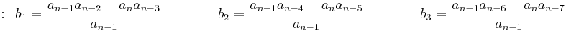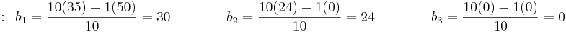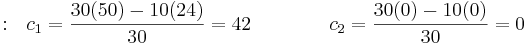10.7: Estabilidad de ruta - Rangos de valores de parámetros que son estables
- Page ID
- 85570
Introducción
La estabilidad de un sistema de control de procesos es extremadamente importante para el proceso de control general. La estabilidad del sistema es un tema clave de seguridad en la mayoría de los procesos de ingeniería. Si un sistema de control se vuelve inestable, puede conducir a condiciones inseguras. Por ejemplo, la inestabilidad en los procesos de reacción o reactores puede llevar a reacciones desbocadas, resultando en consecuencias económicas y ambientales negativas.
La estabilidad absoluta de un proceso de control se puede definir por su respuesta a una perturbación externa al sistema. El sistema puede considerarse estable si existe en un estado consistente o punto de ajuste y regresa a este estado inmediatamente después de una perturbación del sistema. Para determinar la estabilidad de un sistema, a menudo se deben determinar los valores propios de la matriz que representan el conjunto gobernante de ecuaciones diferenciales del sistema. Desafortunadamente, a veces la ecuación característica de la matriz (el polinomio que representa sus valores propios) puede ser difícil de resolver; puede ser demasiado grande o contener variables desconocidas. En esta situación, un método desarrollado por el matemático británico Edward Routh puede producir la información de estabilidad deseada sin resolver explícitamente la ecuación.
Recordemos que para determinar la estabilidad del sistema solo se necesitan conocer los signos de los componentes reales de los valores propios. Debido a esto, un método que pueda revelar los signos sin el cálculo real de los valores propios a menudo será adecuado para determinar la estabilidad del sistema.
Para revisar rápidamente, los componentes negativos de valor propio real hacen que un sistema regrese a un punto de estado estacionario (donde todas las derivadas parciales son iguales a cero) cuando experimenta perturbaciones. Los componentes reales positivos hacen que el sistema se aleje de un punto estable, y un componente real cero indica que el sistema no se ajustará después de una perturbación. Los componentes imaginarios simplemente indican oscilación con una tendencia general de acuerdo con la parte real. Usando el método de estabilidad de Routh, se puede determinar el número de cada tipo de raíz y así ver si un sistema es estable o no. Cuando existen variables desconocidas en la ecuación, la estabilidad de Routh puede revelar los límites en estas variables que mantienen las raíces negativas.
La matriz Routh
La matriz Routh es un atajo para determinar la estabilidad del sistema. El número de raíces positivas (inestables) se puede determinar sin factorizar ningún polinomio complejo.
Generación de la matriz
El sistema en cuestión debe tener una ecuación característica de naturaleza polinomial. como se muestra a continuación:
\[P(S) = a_{n}S^n + a_{n-1}S^{n-1} + \cdots + a_{1}S+ a_0 \nonumber \]
Para examinar las raíces, establezca P (S) =0, lo que le permitirá decir cuántas raíces hay en el plano izquierdo, plano derecho y en el eje j-omega. Si el sistema involucra funciones trigonométricas, debe ajustarse a un polinomio a través de una expansión de la serie Taylor. Una condición necesaria para la estabilidad es que 0\ qquad "src=”/@api /deki/files/18713/image-273.png “>. (Si
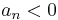 , todos los coeficientes pueden multiplicarse por -1 antes de verificar). La otra condición es que todos los valores en la columna 1 de la matriz Routh deben ser positivos para que el sistema sea estable.
, todos los coeficientes pueden multiplicarse por -1 antes de verificar). La otra condición es que todos los valores en la columna 1 de la matriz Routh deben ser positivos para que el sistema sea estable.
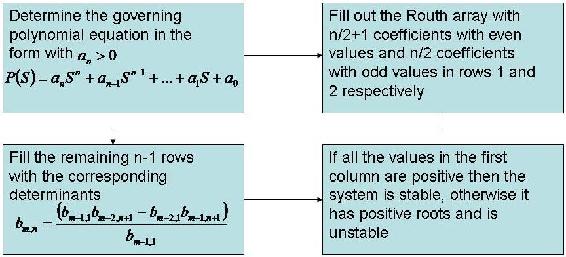
Este diagrama de flujo muestra la generación de una matriz Routh para un caso idealizado con m, n representando la ubicación en la matriz.
Los coeficientes del polinomio se colocan en una matriz como se ve a continuación. El número de filas es una más que el orden de la ecuación. El número de cambios de signo en la primera columna indica el número de raíces positivas para la ecuación.
| Fila 1 | \[\\ \ a_{n } \ \ \qquad a_{n-2} \ \qquad a_{n-4} \qquad ... \nonumber \] |
| Fila 2 | \[\\ \ a_{n-1} \qquad a_{n-3} \qquad a_{n-5} \qquad ... \nonumber \] |
| Fila 3 | \[\\ \ b_1 \qquad \qquad b_2 \ \ \qquad b_3 \ \qquad \ ... \nonumber \] |
| Fila 4 | \[\\ \ c_1 \qquad \qquad c_2 \ \ \qquad c_3 \ \qquad \ ... \nonumber \] |
 |
\[\\ \ \vdots \qquad \quad \qquad \vdots \qquad \ \ \ \vdots \; \; \qquad \ \ \vdots \nonumber \] |
| Fila 5 | \[\\ \ p_1 \qquad \qquad p_2 \nonumber \] |
| Fila 6 | \[\\ \ q_1 \qquad \nonumber \] |
| Fila 7 | \[\\ \ v_1 \qquad \nonumber \] |
En la matriz, las variables b1, b2, c1, c2, etc. se determinan calculando un determinante utilizando elementos de las dos filas anteriores como se muestra a continuación:
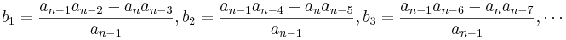
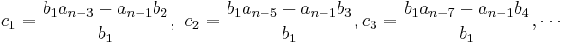
La expresión general para cualquier elemento x después de las dos primeras filas con índice (m, n) es la siguiente:
Para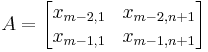
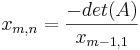
Tenga en cuenta que si la matriz Routh comienza con un cero, aún puede resolverse (asumiendo que todos los demás valores de la fila no son cero), reemplazando el cero por una constante, y dejando que esa constante sea igual a un número positivo muy pequeño. Las filas subsiguientes dentro de esa columna que tengan esta constante se calcularán en función de la constante seleccionada.
Una vez que la matriz esté completa, aplique los siguientes teoremas para determinar la estabilidad:
- Si todos los valores en la primera columna de la matriz Routh son >0, entonces P (S) tiene todas las raíces reales negativas y el sistema es estable.
- Si algunos de los valores de la primera columna de la matriz Routh son <0, entonces el número de veces que el signo cambia hacia abajo en la primera columna será = el número de raíces reales positivas en la\(P(S)\) ecuación.
- Si hay 1 par de raíces en el eje imaginario, ambas a la misma distancia del origen (es decir, equidistantes), entonces verifica para ver si todas las demás raíces están en el plano de la izquierda. Si es así, entonces la ubicación de raíces imaginarias se puede encontrar usando AS 2 + B = 0, donde A y B son los elementos en la matriz Routh para la 2da a la última fila.
Para aclarar aún más, se analiza un ejemplo con números reales.
El siguiente polinomio se generó a partir de un sistema de muestreo.
\[P(S) = 5S^3 -10S^2 + 7S+ 20 \nonumber \]
El polinomio anterior debe ser investigado para determinar la estabilidad del sistema. Esto se hace generando una matriz Routh de la manera descrita anteriormente. La matriz como resultado de este polinomio es,
| Fila 1 | \[\\ \ \ 5 \qquad 7 \nonumber \] |
| Fila 2 | \[\\ -10 \ \ \ \ 20 \nonumber \] |
| Fila 3 | \[\\ \ \ 17 \nonumber \] |
| Fila 4 | \[\\ \ \ 20 \nonumber \] |
En la matriz mostrada anteriormente, el valor que se encuentra en la tercera fila se calcula de la siguiente manera. 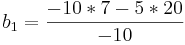 La matriz ahora puede ser analizada. Al mirar hacia abajo la primera columna, se puede ver que 5 es de magnitud positiva, luego el signo cambia en la entrada -10, y el signo cambia por segunda vez a positivo 17. Esto cuenta como dos cambios en el signo, lo que corresponde a dos raíces positivas, haciendo que el sistema sea inestable.
La matriz ahora puede ser analizada. Al mirar hacia abajo la primera columna, se puede ver que 5 es de magnitud positiva, luego el signo cambia en la entrada -10, y el signo cambia por segunda vez a positivo 17. Esto cuenta como dos cambios en el signo, lo que corresponde a dos raíces positivas, haciendo que el sistema sea inestable.
Búsqueda de valores de parámetros de control estables
A menudo, para una operación de unidad, un parámetro PID como la ganancia del controlador (K c), la constante de tiempo integral (T i) o la constante de tiempo derivada (T d) crea una variable adicional en la ecuación característica. Esto se puede llevar a través de los cálculos de la matriz Routh para indicar qué valores de la variable proporcionarán estabilidad al sistema mediante la prevención de que se produzcan raíces positivas en la ecuación. Por ejemplo, si la salida de un controlador se rige por la función:
\[ 10s^3 + 5s^2 + 8s + (T_d + 2) \nonumber \]
Los valores estables de T d se pueden encontrar a través de una matriz Routh:
| Fila 1 | \(\quad 10 \qquad\quad 8\) |
| Fila 2 | \(\quad 5 \ \qquad \ \ \ (T_d + 2)\) |
| Fila 3 | \( \ \ 4-2T_d\) |
| Fila 4 | \((T_d + 2)\) |
\(-2 < T_d < 2 \qquad \)Revelamos para mantener los elementos de la primera columna positivos, por lo que este es el rango estable de valores para este parámetro.
Si hubiera múltiples parámetros en la ecuación, simplemente se resolverían para como grupo, produciendo restricciones a lo largo de las líneas de “T i + K c > 2" etc, por lo que cualquier valor elegido para un parámetro daría un rango estable diferente para el otro.
Casos Especiales
Hay algunos casos especiales que uno debe tener en cuenta al usar la prueba de Routh. Estas varianzas pueden surgir durante el análisis de estabilidad de diferentes sistemas de control. Cuando se encuentra un caso especial, los métodos de solución de estabilidad de Routh tradicionales se alteran como se presenta a continuación.
Uno de los coeficientes en la ecuación característica es igual a cero
Si la potencia del 0*S n es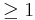 , sustituir el cero por una cantidad, ε, que sería positiva y se acercará a cero. Después continúe con su análisis con normalidad. Esencialmente esto da el límite de las raíces a medida que ese coeficiente se acerca a cero. (Si la potencia = 0, ver Caso 3). Por ejemplo,
, sustituir el cero por una cantidad, ε, que sería positiva y se acercará a cero. Después continúe con su análisis con normalidad. Esencialmente esto da el límite de las raíces a medida que ese coeficiente se acerca a cero. (Si la potencia = 0, ver Caso 3). Por ejemplo,
Ecuación: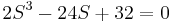
Ecuación de trabajo: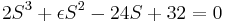
| Fila 1 | \[\quad 2 \quad \quad \quad -24 \nonumber \] |
| Fila 2 | \[\quad \epsilon \quad \quad \quad 32 \nonumber \] |
| Fila 3 | \[\\frac{-24\epsilon-64}{\epsilon} \ \quad \qquad 0 \nonumber \] |
| Fila 4 | \[\\qquad 32 \nonumber \] |
Ya que ε es positivo sabemos que en la primera columna la fila 2 será positiva, la fila 4 será positiva y la fila 3 será negativa. Esto significa que tendremos un cambio de señal de 2 a 3 y nuevamente de 3 a 4. Debido a esto, sabemos que dos raíces tendrán componentes reales positivos. Si realmente factoriza la ecuación lo ve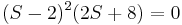 , demostrando que sí tenemos 2 raíces positivas. Ambas raíces son iguales a 2, por lo que técnicamente solo hay una raíz, pero en cualquier caso sabemos que el sistema es inestable y debe ser rediseñado.
, demostrando que sí tenemos 2 raíces positivas. Ambas raíces son iguales a 2, por lo que técnicamente solo hay una raíz, pero en cualquier caso sabemos que el sistema es inestable y debe ser rediseñado.
Una de las raíces es cero
Este caso debería ser obvio simplemente por mirar el polinomio. El término constante faltará, es decir, la variable puede ser factorizada a partir de cada término. Si agregaste un ε al final como en el caso 1, la última fila sería ε e indicaría falsamente otro cambio de signo. Realizar análisis de Routh con el último cero en su lugar.
Ecuación: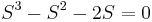
| Fila 1 | \[\\ \ 1 \ \ \ -2 \nonumber \] |
| Fila 2 | 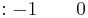 |
| Fila 3 | 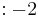 |
| Fila 4 | \[\\ \ 0 \qquad \nonumber \] |
Como puede ver en la columna uno tenemos fila 1 positiva, fila 2 y 3 negativa, y fila 4 cero. Esto se interpreta como un cambio de signo, dándonos una raíz real positiva. Mirando esta ecuación en forma factorizada,
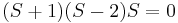
podemos ver que efectivamente tenemos sólo una raíz positiva igual que equivale a 2. El cero en la última fila indica una raíz inestable adicional de cero. Alternativamente, puede resultarle más fácil simplemente factorizar la variable y encontrar los signos de los valores propios restantes. Solo recuerda que hay una raíz extra de cero.
Fila llena de ceros
Cuando esto sucede sabes que tienes o un par de raíces imaginarias, o raíces reales simétricas. La fila de ceros debe ser reemplazada. El siguiente ejemplo ilustra este procedimiento.
Ecuación: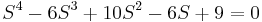
| Fila 1 | \[\\ \ 1 \qquad \qquad 10 \qquad \qquad 9 \nonumber \] |
| Fila 2 |  |
| Fila 3 | \[\\ \ 9 \qquad \qquad 9 \nonumber \] |
| Fila 4 | \[\\ \ 0 \qquad \qquad 0 \nonumber \] |
La fila 4 contiene todos los ceros. Para determinar sus valores de reemplazo, primero escribimos un polinomio auxiliar A determinado por las entradas en la Fila 3 anterior.
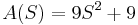
Observe que el orden disminuye en 1 a medida que bajamos de la tabla, pero disminuye en 2 a medida que cruzamos.
Luego tomamos la derivada de este polinomio auxiliar.
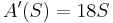
Los coeficientes obtenidos después de tomar la derivada nos dan los valores utilizados para sustituir a los ceros. A partir de ahí, podemos proceder a los calcuaciones de tabla normalmente. La nueva tabla es
| Fila 1 | \[\\ \ 1 \qquad \qquad 10 \qquad \qquad 9 \nonumber \] |
| Fila 2 |  |
| Fila 3 | \[\\ \ 9 \qquad \qquad 9 \nonumber \] |
| Fila 4 | \[\\ \ 18 \qquad \qquad 0 \nonumber \] |
| Fila 5 | \[\\ \ 9 \qquad \qquad \nonumber \] |
De hecho, las raíces reales puramente imaginarias o simétricas del polinomio original son las mismas que las raíces del polinomio auxiliar. Así, podemos encontrar estas raíces.
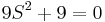
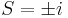
Debido a que tenemos dos cambios de signo, sabemos que las otras dos raíces del polinomio original son positivas.
De hecho, después de factorizar este polinomio, obtenemos
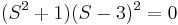
Por lo tanto, las raíces son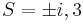 , donde en este caso, la raíz 3 tiene multiplicidad 2.
, donde en este caso, la raíz 3 tiene multiplicidad 2.
Limitaciones
Las matrices Routh son útiles para clasificar un sistema como estable o inestable en función de los signos de sus valores propios, y no requieren computación compleja. Sin embargo, la simple determinación de la estabilidad no suele ser suficiente para el diseño de sistemas de control de procesos. Es importante desarrollar el grado de estabilidad así como lo cerca que está el sistema a la inestabilidad. Otros análisis de estabilidad no contabilizados en la técnica de análisis de Routh incluyen encontrar el grado de estabilidad, el rendimiento en estado estacionario del sistema de control y la respuesta transitoria del sistema a las perturbaciones.
Se deben utilizar técnicas más involucradas, como las discutidas en Valores propios y vectores propios, para caracterizar aún más la estabilidad del sistema (con la excepción de los polinomios del sistema que dan como resultado raíces imaginarias puras). Otra limitación del método Routh se produce cuando el polinomio en cuestión se vuelve tan grande que la estabilidad de Routh consume demasiado tiempo computacionalmente (un juicio personal). Para esta situación, se debe utilizar otro método, como una gráfica de locus raíz.
Tenga en cuenta que para definir la estabilidad, siempre comenzaremos con un polinomio. Este polinomio surge de encontrar los valores propios del modelo linealizado. Así nunca nos encontraremos con otras funciones, digamos funciones exponenenciales o funciones de pecado o cos en general para el análisis de estabilidad en la teoría de control.
Ventajas sobre las parcelas de locus radicular
La estabilidad de Routh evalúa los signos de las partes reales de las raíces de un polinomio sin resolver por las propias raíces. El sistema es estable si todas las partes reales son negativas. Por lo tanto, a diferencia de las gráficas de locus raíz, no es necesario calcular los valores propios reales para un análisis de estabilidad de Routh. Además, a veces el sistema tiene demasiadas incógnitas para construir e interpretar fácilmente una gráfica de locus raíz (por ejemplo, con dos controladores PID están las variables Kc1, Kc2, τi1, τi2, τd1 y τd2).
Supongamos que el siguiente polinomio describe los valores propios de un modelo linealizado de su proceso. Para este polinomio, ¿completar una matriz Routh y determinar la estabilidad del sistema?
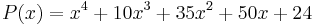
Respuesta
Dado que P (X) es un polinomio de cuarto orden, la matriz Routh contiene cinco filas.
Fila 1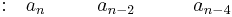 |
Fila 2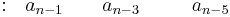 |
Fila 3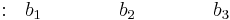 |
Fila 4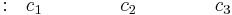 |
Fila 5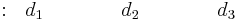 |
Las filas 1 y 2 corresponden a los coeficientes de los términos polinomiales:
Fila 1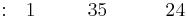 |
Fila 2 |
Las filas 3, 4 y 5 contienen los determinantes utilizando elementos de las dos filas anteriores.
|
Fila 3 |
|
Fila 4 |
Fila 5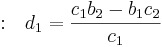 |
Por lo tanto,
|
Fila 3 |
|
Fila 4 |
Fila 5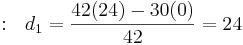 |
La matriz completa de Routh:
Fila 1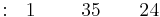 |
Fila 2 |
Fila 3 |
Fila 4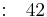 |
Fila 5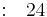 |
Dado que todos los valores de la primera columna son positivos, la ecuación P (x) tiene todas las raíces negativas y el sistema es estable.
Considere un sistema con la siguiente ecuación característica:
\[20s^3+59s^2+46s+(4+K_c)=0 \nonumber \]
Usando un controlador solo P, encuentre el rango de ganancia del controlador que producirá un sistema estable.
Responder
Dado que la ecuación es un polinomio de tercer orden, la matriz Routh tiene cuatro filas. Matriz Routh:
| Fila 1 | \[\\ \qquad \;20 \qquad \qquad \qquad 46 \qquad \nonumber \] |
| Fila 2 | \[\\ \qquad \;59 \qquad \qquad \qquad (4+K_c)\qquad \nonumber \] |
| Fila 3 | \[\\ \;46 - \frac{20}{59}(4+K_c) \quad \ \quad 0 \nonumber \] |
| Fila 4 | \[\\ \ \ \ \ \;(4+K_c) \qquad \qquad \ 0 \nonumber \] |
Para que el sistema sea estable, todos los elementos de la primera columna de la matriz Routh tienen que ser positivos.
La primera columna contendrá solo elementos positivos si:
0" src=”/@api /deki/files/18855/image-349.png “>
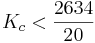
0\ qquad” src=”/@api /deki/files/18859/image-351.png “>
-4\ qquad” src=”/@api /deki/files/18861/image-352.png “>
Rango estable aceptable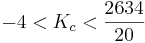
Considere un sistema con la siguiente ecuación característica:
\[s^5-3s^4+s^3+s^2+4=0 \nonumber \]
Determinar la estabilidad de este sistema.
Respuesta
Uno de los coeficientes en la ecuación característica es igual a 0. Sustituimos el cero por una cantidad que sería positiva (acercamos a cero desde el lado derecho) y continuamos con el análisis como normal.
Ecuación de trabajo:
\[s^5-3s^4+s^3+s^2+ \epsilon s+4=0 \nonumber \]
| Fila 1 | \[\\ \ \ 1 \qquad \qquad \qquad \qquad 1\qquad \qquad \epsilon \nonumber \] |
| Fila 2 |  |
| Fila 3 | \[\\ \frac{4}{3} \ \qquad \qquad \qquad \quad \epsilon + \frac {4}{3} \nonumber \] |
| Fila 4 | \[\\ \ 4+ \frac{9\epsilon}{4} \ \qquad \qquad \qquad 4 \nonumber \] |
| Fila 5 | \[\\ \epsilon + \frac {4}{3} - \frac{64}{27\epsilon+48} \qquad 0 \nonumber \] |
| Fila 6 | \[\\ 4 \nonumber \] |
Dado que ε es positivo, en la primera columna, hay dos cambios de signo, de la fila 1 a la fila 2 y de la fila 2 a la fila 3. Así, sabemos que las raíces tendrán dos componentes reales positivos. Si realmente factoriza la ecuación verá eso,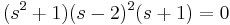 , demostrando que sí tenemos dos raíces positivas, ambas iguales a 2.
, demostrando que sí tenemos dos raíces positivas, ambas iguales a 2.
Existe complicación adicional porque en la fila 5, como ε va a cero, el término también va a cero, lo que significa que para la fila 5, estamos obteniendo una fila llena de ceros. Esto significa que tenemos un par de raíces imaginarias, y esta situación se puede resolver usando la ecuación,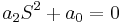 .
.
En este caso, la ecuación de trabajo es,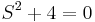
Las raíces imaginarias son,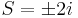
Eres ingeniero en una fábrica de helado. Hay una cuba de almacenamiento con un sistema de enfriamiento que tiene un esquema de controlador PI. Tiene la siguiente ecuación característica:
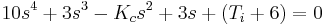
Su trabajo es determinar las restricciones sobre los valores K c y T i de manera que el sistema sea estable.
Respuesta
El objetivo es hacer que la matriz sea tal que la primera columna no tenga cambios de signo. Dado que las dos primeras entradas de la primera columna son números y positivas, por lo tanto, todos los demás valores de esta columna deben ser positivos.
Ecuación de trabajo: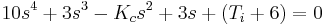
| Fila 1 | \[\\ 10 \qquad \qquad \qquad \qquad -K_c \qquad \qquad T_i+6 \nonumber \] |
| Fila 2 | \[\\ 3\qquad \qquad \qquad \qquad \qquad 3\qquad \nonumber \] |
| Fila 3 | \[\\ 10-K_c \ \qquad \qquad \qquad T_i+6 \nonumber \] |
| Fila 4 | \[\\ 3- \frac{3(T_i+6)}{(10-K_c)} \qquad \qquad 0 \nonumber \] |
| Fila 5 | \[\\ T_i+6 \nonumber \] |
Ya que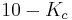 está en la primera columna, da la restricción
está en la primera columna, da la restricción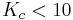 . Asimismo,
. Asimismo,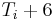 debe ser positivo, dando la restricción
debe ser positivo, dando la restricción -6\,” src=”/@api /deki/files/18907/image-375.png “>. Lo que trae la entrada final de
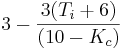 . Dividiendo por tres y reordenamiento de los términos, se ve eso
. Dividiendo por tres y reordenamiento de los términos, se ve eso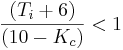 . Luego se reordenan los términos para llegar a la desigualdad:
. Luego se reordenan los términos para llegar a la desigualdad: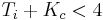 .
.
Referencias
- Bequette, W.B. Control de Procesos Modelado Diseño y Simulación., New Jersey: Prentice Hall, pp 170-178.
- Foecke, H.A. y Weinstein, A. “Raíces complejas a través de raíces reales y raíces cuadradas usando el criterio de estabilidad de Routh”. arxiv.org, 5 de enero de 2007.
- Liptak, Bela G., Control y Optimización de Procesos. Vol. II. Nueva York: Taylor & Francis.
- Ogunnaike, Babatunde A.; Ray, W. Harmon. Dinámica de Procesos, Modelado y Control. Nueva York Oxford: Oxford University Press, 1994.
Colaboradores
- Autores: John D'Arcy, Matt Hagen, Adam Holewinski y Alwin Ng
- Administradores: Jeff Falta, Taylor Lebeis, Shawn Mayfield, Marc Stewart, Tom Welch