10.6: Parcelas de Locus Raíz - Efecto de Afinación
- Page ID
- 85569
Introducción
Las gráficas de locus radiculares muestran las raíces de la ecuación característica de los sistemas, (es decir, la Laplaciana), en función de las variables de control tales como\(Kc\). Al examinar estas gráficas es posible determinar la estabilidad de diferentes valores de la variable de control. Una función de transferencia típica es de la forma\(G(s) = Y(s)/U(s)\).
- Polos: U (s) = 0
- Ceros: Y (s) = 0
Es decir, después de la factorización los polos son las raíces de los denominadores y los ceros son las raíces del numerador. La estabilidad solo depende del valor de los polos. El sistema es estable para todos los valores de las variables de control que dan como resultado que el valor de la parte real de cada valor de polo sea menor que cero.Las líneas de una gráfica de locus raíz muestran los polos para los valores de la (s) variable (s) de control de cero a infinito en un sistema de coordenadas complejo. Estas parcelas siempre tendrán una línea de simetría en\(i = 0\).
Bucle cerrado frente a bucle abierto
Un sistema de bucle cerrado utiliza control de retroalimentación donde la salida tiene un efecto en la entrada. Con un bucle cerrado, generalmente se introducen oscilaciones, y por lo tanto pueden volverse inestables. A diferencia de los sistemas de bucle abierto, el circuito cerrado incorpora válvulas y controladores.
En un sistema de bucle abierto, la salida no se compara y no tiene ningún efecto sobre la entrada. En un sistema de bucle abierto, las oscilaciones no se introducen y por lo tanto no pueden volverse inestables. Un sistema de bucle abierto, sin embargo, puede ser inexacto porque no toma en cuenta la dinámica de control. Los sistemas de bucle abierto incluirán esquemas de control de avance o esquemas de control cronometrados. Los dos diagramas a continuación representan esta diferencia al intentar controlar la temperatura en su departamento. (Haga clic en las imágenes para aumentar la resolución).
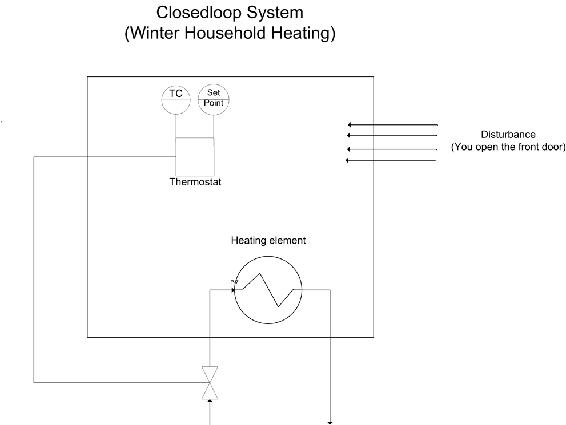
En este diagrama un termostato presenta retroalimentación al calentador para encenderlo o apagarlo.
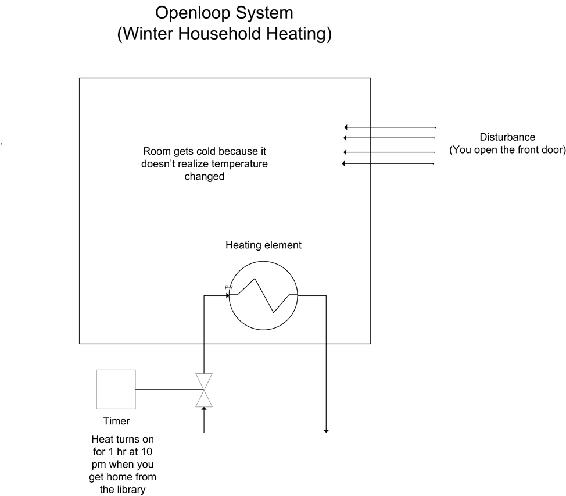
Dado que el calentador solo se enciende a las 10 de la tarde, se supone que la cantidad de tiempo que abras la puerta será la misma cada día. Se considera un sistema abierto ya que la temperatura en la habitación es independiente del controlador del calentador.
Tenga en cuenta que todos los ejemplos presentados en esta página web discuten los sistemas de bucle cerrado porque incluyen todos los sistemas con retroalimentación.
Sistemas de coordenadas complejos
Las gráficas de locus raíz son una gráfica de las raíces de una ecuación característica en un sistema de coordenadas complejo. Un sistema de coordenadas complejo permite trazar un número complejo con partes tanto reales como imaginarias. El componente real se traza en el eje x y el componente imaginario se traza en el eje y. Al crear parcelas de locus radicular se deben resolver raíces imaginarias para. Estas raíces imaginarias vienen en pares conjugados complejos (esto se puede ver a continuación en la sección sobre “Trazado de polos en un sistema de coordenadas complejo para hacer una gráfica de locus raíz”).
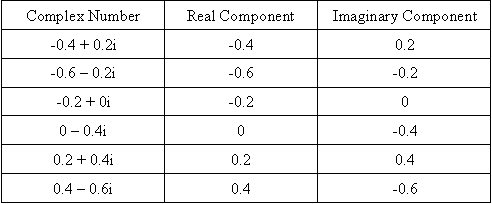
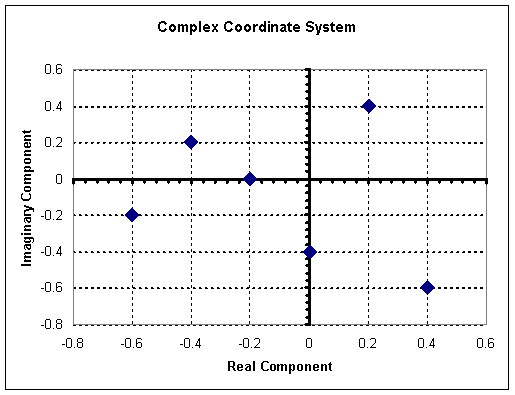
Por ejemplo, a continuación se muestra una gráfica de los siguientes números complejos. Estos números complejos pueden dividirse en los componentes reales e imaginarios para facilitar la trama.
Desarrollo de una ecuación característica
Aunque el objetivo de este artículo es discutir las parcelas de locus raíz, es necesario mencionar brevemente cómo determinar la ecuación característica de un sistema para obtener la gráfica de locus raíz. En general, la mayoría de los procesos de ingeniería química pueden ser descritos por un sistema de ecuaciones diferenciales ordinarias. Siga los siguientes pasos para determinar la ecuación característica para el sistema (que le permitirá desarrollar una gráfica de locus raíz).
- Si las ODE no son lineales, linealizarlas. (Consulte este enlace para obtener más información sobre linealización de ODEs <controls.engin.umich.edu/wiki/index.php/LinearizingODEs>)
- Después de linealizar las ODEs, use álgebra matricial para encontrar los valores propios de su sistema. Tenga cuidado aquí de no insertar valores numéricos para sus parámetros de control, (por ejemplo, deje Kc como Kc, no Kc=1). (Para más información sobre cómo encontrar valores propios <controls.engin.umich.edu/wiki/index.php/EigenvaluesEigenvectors>)
- La ecuación polinómica obtenida para el valor propio debe contener lambda y los parámetros de control. Esta ecuación es la ecuación característica. Obtener soluciones a esta ecuación estableciendo valores para los parámetros de control y resolviendo para los valores propios. Las raíces obtenidas serán utilizadas para crear el diagrama de locus radicular.
Este proceso de 3 pasos es válido para obtener una ecuación característica para cualquier sistema de control de bucle cerrado. Un método más tradicional para desarrollar ecuaciones características es aplicar transformaciones de Laplace.
Laplace Transforma
Las transformaciones de Laplace son un método para cambiar ecuaciones diferenciales lineales ordinarias en función de transferencia. Todas las funciones de transferencia utilizadas en las gráficas de locus raíz son independientes del tiempo porque\(L[f(t)] ≣ F(s)\). Formally, the equation below shows that the time function is integrated, leaving only the variable \(s\).
\[\mathbf{F}(\mathbf{s})=\int_{0}^{\infty} f(t) e^{-s t} d t \nonumber \]
s es un número complejo, por lo que nos permite construir gráficas complejas de sistemas de coordenadas. La solución exacta a la mayoría de las perturbaciones y controladores se puede encontrar en cualquier libro de controles. Por favor, consulte siempre su libro de matemáticas de ecuaciones diferenciales ordinarias para obtener más información sobre las transformaciones de Laplace.
Se debe determinar la estabilidad de los reactores químicos en serie. Los reactores están bien mezclados e isotérmicos, y la reacción es de primer orden en el componente A. La concentración de salida del segundo reactor se controla con un algoritmo de retroalimentación PI que manipula el flujo del reactivo, que es mucho menor que el flujo del disolvente. El sensor y el elemento final se suponen rápidos, y los datos del proceso son los siguientes.
Proceso
- V= 5m 3
- FS=5M 3 /min >> FA
- k = 1 min -1
- vs= 50% abierto
- CA 0 = 20 moles/m 3
- CA 0 (s) /v (s) = Kv= 0.40 (moles/ m 3) (%abierto)
- Controlador PI Kc =?? Tf = 1 min
Formulación La función de transferencia para el proceso y el controlador son
\[G_{y}(s)=\frac{K_{y}}{(\tau s+1)(\tau s+1)} \nonumber \]
\[G_{c}(s)=K_{c}\left(1+\frac{1}{T_{f} s}\right) \nonumber \]
\[K_{y}=K_{v}\left(\frac{F}{F+V k}\right)=0.1 \frac{m o l e / m^{3}}{\%} \nonumber \]
\[\tau=\frac{V}{F+V R}=0.5 \mathrm{min} \nonumber \]
Las funciones de transferencia individuales se pueden combinar para dar la función de transferencia de bucle cerrado para un cambio de punto de ajuste, que incluye la ecuación característica. (donde CV= Variable de control y SP = señal de punto de ajuste)
\[\frac{C V(s)}{S P(s)}=\frac{G_{p}(s) G_{v}(s) G_{c}(s)}{1+G_{r}(s) G_{v}(s) G_{c}(s) G_{s}(s)}=\frac{K_{p}\left(1+\frac{1}{s}\right) \frac{0.1}{(0.5 s+1)^{2}}}{1+K_{p}\left(1+\frac{1}{s}\right) \frac{0.1}{(0.5 s+1)^{2}}} \nonumber \]
Ecuación característica
\[0=1+K_{p}\left(1+\frac{1}{s}\right) \frac{0.1}{(0.5 s+1)^{2}} \nonumber \]
Diagramas de locus raíz
Las parcelas de locus radicular son un método para evaluar el comportamiento de un sistema de control. La creación de una gráfica de locus raíz comienza determinando los polos del sistema de control para un conjunto dado de parámetros de control. Estos polos se trazan luego en un sistema de coordenadas complejo como se ve en la sección anterior y se analizan para determinar el comportamiento del sistema.
Determinación de los polos de un sistema de control
Los “polos” de un sistema son las raíces del demoninador de la función de transferencia. En otras palabras, los polos son los valores de “s” cuando la función de transferencia va al infinito (cuando el demoninador es igual a cero). Para un sistema de ecuaciones diferenciales, los polos son los valores propios del sistema de ecuaciones. Considere la siguiente solución a un sistema de ecuaciones diferenciales:
\[f(s) = 48s^3 + 44s^2 + 12s + 1 \label{eq1} \]
Esta ecuación es un polinomio de tercer orden, por lo tanto tendrá tres polos (tenga en cuenta que algunos de estos polos pueden ser números imaginarios). Estos polos se pueden obtener factorizando la expresión o usando un programa de computadora como Maple. Los tres polos, o raíces, de esta ecuación son s = -0.167, -0.25, -0.5.
Para un sistema de ecuaciones diferenciales, encontrar los valores propios puede llevar mucho tiempo y el uso de Matlab, Maple o Mathematica es más eficiente. Un método sería usar la función de valores propios de Mathematica [] para resolver el sistema por usted. Esta función se explica en la sección Eigenvalues y Eigenvectors del texto wiki.
Trazado de polos en un sistema de coordenadas complejo para realizar un trazado de locus raíz
Se crea una gráfica de locus raíz trazando los polos resultantes en un sistema de coordenadas complejo. Para el sistema de control solo P, las ecuaciones diferenciales gobernantes dependerán de la ganancia proporcional, Kc. Considere la siguiente solución a un sistema de ecuaciones diferenciales:
\[f(s)=48 s^{3}+44 s^{2}+12 s+1+6 Kc \label{2} \]
Observe que Kc es un término en esta ecuación. Por lo tanto, existe un conjunto de polos para cada valor de Kc. Si Kc = 0, entonces la ecuación #2 se reduce a la ecuación #1, y los polos son los enumerados anteriormente. En el Cuadro 1 se enumeran los tres polos del sistema para valores dados de Kc. Estos polos se calcularon utilizando un sistema de álgebra computacional porque no es práctico tratar de evaluar estas funciones con métodos analíticos.
Tabla 1- Postes de Ecuación Característica
Para crear una gráfica de locus raíz, cada polo se divide en su componente real (eje x) e imaginario (eje y) (Tabla 2):
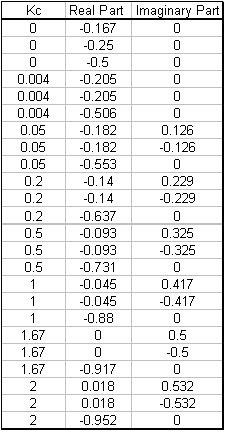
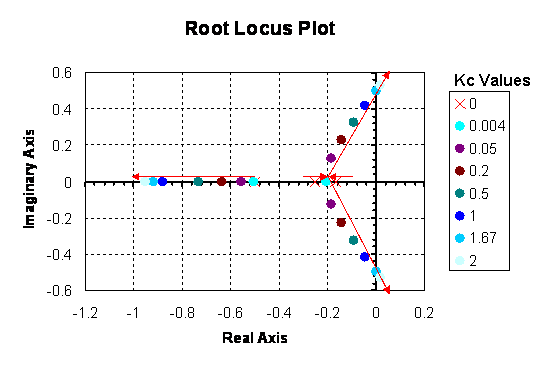
Por convención, las flechas rojas se dibujan en la gráfica en la dirección de aumentar los valores de Kc. Ayudan a ilustrar cómo varían las raíces del sistema cambiando el valor de Kc. También por convención, los puntos en los que Kc = 0 se representan con marcas 'x' en lugar de puntos.
Interpretación de un diagrama de locus raíz
El uso principal de un Diagrama de Locus Raíz es evaluar cómo los diferentes valores de Kc afectan la estabilidad y el comportamiento de un sistema de control.
La estabilidad del sistema de control depende del signo del componente real del polo. Si los componentes reales de todos los polos son negativos, entonces se dice que el sistema es estable para ese valor de Kc. Si el componente real del polo es positivo, el sistema es inestable para ese valor de Kc, lo que significa que la señal de salida divergirá del punto de ajuste.
El comportamiento del sistema de control depende de la presencia de un componente imaginario del polo. Si alguno de los tres polos contiene un componente numérico imaginario, entonces ese valor de Kc hará que la señal de salida oscile. Si todos los polos son reales (no contienen componentes imaginarios), la señal de salida no oscilará a ese valor Kc.
Por favor, consulte el diagrama de Locus Raíz en la Figura 1. El sistema se vuelve inestable (es decir, el componente real de los polos se vuelve positivo) para Kc > 1.67 y Kc < 0. Dentro del rango de estabilidad, no se observan oscilaciones (es decir, ningún componente imaginario) cuando 0 < Kc < 0.004.
Diagramas de locus raíz para control PID
Los diagramas de locus raíz son mucho más difíciles de crear para el control PID. La ecuación característica contendrá variables desconocidas Kc, Ti y Td. Por lo tanto, cada punto del Diagrama de Locus Raíz representará un conjunto de parámetros de ajuste. Para mostrar la progresión a medida que cambia cada parámetro de ajuste, el diagrama resultante será una gráfica de superficie tridimensional. Debido a la complejidad de este diagrama, no vamos a crear uno, ya que está más allá del alcance de este texto. Sin embargo, el análisis de estabilidad aún se puede aplicar a la ecuación característica. Tomemos por ejemplo la Ecuación\ ref {eq3}:
\[f(s)=\frac{48 s^{3}+44 s^{2}+12 s+1+6 K c}{T i+3 T d} \label{eq3} \]
En esta instancia teórica, la ecuación 3 es la ecuación característica que rige el mismo sistema mencionado anteriormente, solo que ahora con control PID. Observe la presencia adicional de los términos Ti y Td. Bajo el control P- solo, este sistema fue estable para valores de Kc entre 0 y 1.67. ¿Será cierto lo mismo si este sistema estuviera sintonizado con control PID?
Supongamos que queremos probar las condiciones Kc = 1.0, Ti = 0.3 y Td = 0.1. Estos valores fueron escogidos al azar. Usando un paquete de software de computadora, se determinó que las tres raíces eran: r1 = -0.827, r2 = -0.044 + 0.417i, r3 = -0.044 — 0.417i. Por lo tanto, dado que los componentes reales son todos negativos, el sistema sigue siendo estable. Dado que las raíces complejas están presentes, se espera que la respuesta oscile alrededor del punto de ajuste.
Creación de gráficas de locus raíz con Mathematica
Mathematica le permite desarrollar parcelas de locus raíz para polinomios ya que las matemáticas involucradas en la resolución de las soluciones pueden llegar a ser muy tediosas. Antes de poder obtener la parcela de locus raíz, debe resolver para las raíces. Utilizaremos la misma ecuación que se utilizó en la sección “Determinación de los polos de un sistema de control”.
\[f(s) = 48s^3 + 44s^2 + 12s + 1 + 6K_c \nonumber \]
La función Solve [] se puede utilizar para determinar las raíces, tanto reales como imaginarias, para cada valor Kc correspondiente. La sintaxis en Mathematica se muestra a continuación para la ecuación especificada cuando Kc = 0. Es importante tener en cuenta que para obtener una salida se debe presionar “Shift Enter”.
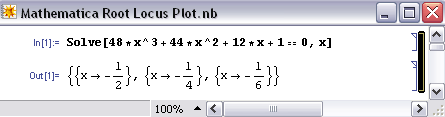
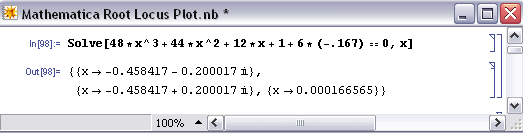
Lo siguiente es solo para mostrar cómo Mathematica formatea la salida cuando\(Kc ≠ 0\) y cuando hay raíces imaginarias. En este caso,\(Kc = -0.167\).
Esto se puede hacer para todos los valores de Kc para obtener las raíces reales e imaginarias correspondientes. Una vez calculadas todas las raíces, se puede hacer una tabla para formatear las raíces reales (eje x) versos raíces imaginarias (eje y). Cuando se usa la sintaxis, A= {{x, y} {a, b}...}, está ingresando todos los valores x e y nombrando esos valores A. Cuando llama a A en la función TableForm [], la tabla se realizará de acuerdo con todos los valores x e y introducidos en A. La sintaxis y los resultados correspondientes se muestran a continuación.
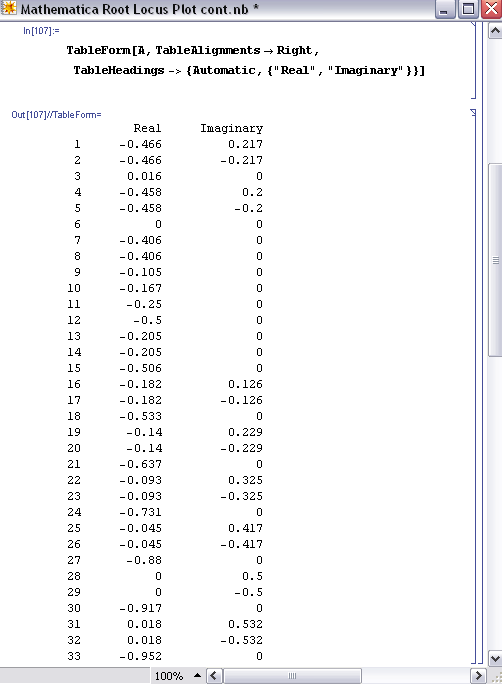
Para producir la tabla que se muestra arriba, solo necesitas TableForm [A] y nada más. Las otras descripciones (es decir. TableAlignments y TableHeadings) solo se utilizan con fines de formateo.
Una vez que las raíces real (x) e imaginaria (y) han sido determinadas y puestas en formato de tabla para su ecuación, la función ListPlot [] se puede utilizar para desarrollar su diagrama de locus raíz llamando a A.
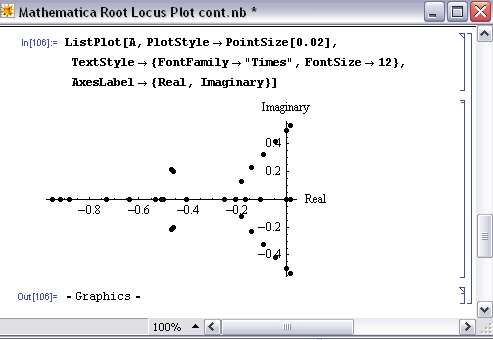
Como puede ver, la función ListPlot [] devolvió la misma gráfica que se muestra en la sección “Sistema de coordenadas complejas para hacer Gráfica de locus raíz” (esta gráfica se creó en Excel). Las flechas no se muestran en esta gráfica de Mathematica; sin embargo, la gráfica de Excel muestra la dirección del aumento de los valores de Kc para mostrar cómo varían las raíces del sistema cambiando los valores de Kc.
El Navegador de Ayuda de Mathematica es una herramienta muy útil para entender la sintaxis. Por ejemplo, al usar la función ListPlot [] puedes buscar cómo etiquetar los ejes y cómo hacer que los puntos sean más grandes (más visibles) en la gráfica. Los siguientes ejemplos se utilizan para ilustrar el uso de parcelas de locus radicular. Haga clic en el siguiente enlace si desea acceder al archivo de Mathematica real: Media:rlpfinalaa.nb
Segundo método de trazado usando matrices
El objetivo aquí es poder entender exactamente lo que está sucediendo con estas entradas de Mathematica con el fin de obtener una mejor comprensión de los resultados. Básicamente, una vez que hayas encontrado los valores propios del sistema, cuyos ejemplos se pueden encontrar en otras áreas de la wiki, entonces queremos resolverlos explícitamente para ellos. Después de resolver para el Eigenvalue en términos de las variables, podemos crear una matriz variando este valor y resolviendo para los términos reales e imaginarios de los valores propios.
Salidas de autovalor en Mathematica
Los valores propios pueden ser devueltos en función de 'l', que es la designación del valor propio o simplemente como una función compleja en términos de variables. Cuando se devuelve como una función de 'l' habrá una entrada polinómica que tiene que simplificarse para encontrar 'l' en función de la variable. En este caso: Kc.
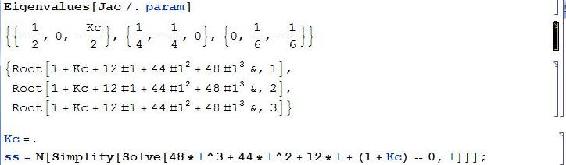
Este ejemplo se toma directamente de la conferencia 17 y su archivo complementario de Mathematica. Lo que está sucediendo aquí es que se ingresó al jacobiano, y hubo múltiples matrices de valores propios que se encontraron. La última matriz tiene tres funciones polinómicas complejas que equivalen a 0. La última línea los está simplificando, resolviendo por 'l'. Esto es poner los Eigenvalues simplificados en la matriz 'ss'.
Otra salida de Eigenvalues es simplemente en forma de números complejos en sí mismos. En lugar de preocuparse por los pasos de simplificación, estos valores propios se pueden ingresar directamente como un número complejo en una matriz, nuevamente denominada 'ss':
Esta es una variación de la muestra en la conferencia 17.
Creación de matriz de trazado
Ahora que hemos visto las dos formas de creación de matrices Eigenvalue, podemos usarlas para crear otra matriz que serán los puntos para la trama. Aquí estaremos sustituyendo en valores de la variable Kc para encontrar diferentes valores de los valores propios, lo que nos dará información sobre los cambios de estabilidad a medida que cambia Kc.
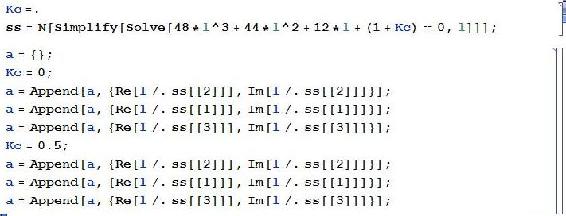
En el ejemplo anterior, 'ss' está en la forma:
Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.06:_Parcelas_de_Locus_Raíz_-_Efecto_de_Afinación), /content/body/div[6]/div[2]/p[3]/span, line 1, column 10
Sin embargo, no todas las matrices de valores propios tendrán el mismo número de valores propios. Por ejemplo, como se mencionó en el párrafo anterior, 'ss' está en la forma:
Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.06:_Parcelas_de_Locus_Raíz_-_Efecto_de_Afinación), /content/body/div[6]/div[2]/p[4]/span, line 1, column 10
Estos diferentes métodos generan matrices de números que actúan esencialmente como valores 'x' e 'y', o en este caso Real e Imaginario, para la trama. La matriz 'a' se traza como tal:
ListPlot [a, PlotStyle -> PointSize [0.02]]
Esto se ingresa directamente a Mathematica, que crea la Gráfica de Locus Raíz.
Ejemplo de ecuación diferencial de parcelas de locus radicular en Mathematica
Un problema de ejemplo extraído del segundo examen de otoño de 2008:
“Te acaban de poner a cargo de diseñar un biorreactor a gran escala para la producción de un fármaco a base de proteínas de gran éxito. Después de algunas investigaciones, se le ha ocurrido el siguiente modelo para describir el sistema reactor:”
\[\dfrac{dX}{dt} = − 2X + \dfrac{10 X S}{S + 2} \nonumber \]
\[\dfrac{dS}{dt} = 4 Fin − S − \dfrac{3 X S}{S + 2} \nonumber \]
\[\dfrac{dP}{dt} = 9 X − 2 P \nonumber \]
donde\(X\) está la concentración celular,\(S\) es la concentración de nutrientes, y\(P\) es el producto proteico. \(Fin\)es el caudal de nutriente en el sistema.
En este sistema se encuentran dos puntos fijos estableciendo todas las ecuaciones diferenciales iguales a cero y resolviendo en Mathematica.
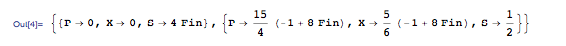
Los dos puntos fijos dependen del valor de Fin y con eso los valores variables de Fin cambiarán eventuales valores propios. Dado que este problema eventualmente querrá gráficas de locus raíz para ambos puntos fijos, es más fácil guardar ambos puntos como parámetros para ser aplicados a ecuaciones generales posteriormente. En general, ayudará a salvar la necesidad de código redundante. Todo el archivo Mathematica al que se hace referencia en este ejemplo está disponible aquí: Media:Exam2PROB1.nb
A partir de este punto se debe crear una matriz jacobiana para linealizar el sistema alrededor de los puntos fijos (tal como se aplica al jacobiano). Una vez creados, se pueden aplicar los valores de punto fijo almacenados para X, S y P. Una vez aplicados, los valores propios para cada punto fijo se pueden resolver para. Estos seguirán contendrán una variable 'Fin' ya que Fin aún no se ha definido.
A partir de aquí la función Table [] se puede utilizar para tabular valores propios para diversos valores de Fin para fines visuales de inspección. Esto no es necesario ya que los resultados del valor propio ya han sido resueltos en términos de Fin. Para crear las gráficas de locus raíz, los valores de Fin deben definirse y aplicarse a las ecuaciones de valores propios con los resultados almacenados. Ese paso es el siguiente. En este paso de tabla es por el bien del usuario ver con el aumento de los valores Fin cómo se ven los valores propios. Los valores propios tabulados se almacenan como una matriz y se muestran como tales con la función 'MatrixForm [
Estas tablas hacen que sea fácil ver con el aumento de Fin (va de 0 a 2 abajo de la tabla) cuáles son los cambios en la estabilidad de cada punto fijo. El primer cuadro es el primer punto fijo, el segundo cuadro el segundo FP.
Ahora bien, para hacer las gráficas de locus raíz, se necesita crear una cadena de valores realmente larga para que se trazen las raíces reales e imaginarias. Esta es una larga cadena de código que es básicamente fuerza bruta. La acción general que ocurre aquí es establecer Fin en un valor, evaluar esa Fin a través de los valores propios y guardar la porción real separada de la porción imaginaria por diferentes columnas. Esto se repite para tantos valores de Fin como se desee. Es extremadamente repetitivo, pero funciona. Después de evaluar tantos valores de Fin como desee, puede mostrar las dos columnas a través de la función ListPlot []. Los fragmentos de ejemplo del código se ven así:
Y la función ListPlot [] puede verse así:
Y harían gráficas como estas (Punto Fijo 1 en la parte superior y FP2 en la parte inferior en este ejemplo):
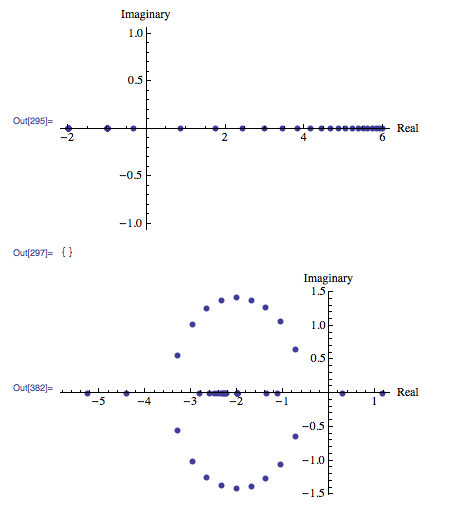
Mirando hacia atrás en las tablas de valores propios, las parcelas pueden ser interpretadas. Para FP1 los valores comienzan negativos reales y aumentan a positivos reales. No hay valores imaginarios. Para FP2, los valores crecientes de Fin pasan de positivo real a negativo con valores imaginarios que ocurren en la transición de valores de Fin bajos a altos.
Método alternativo de Mathematica
Algunos programas de Mathematica 6 tienen una aplicación complementaria o complementaria conocida como INSYDES ANALOG que contiene opciones especiales para crear Gráficas de Locus Raíz con facilidad. La función se llama rootLocusPlot. Ingresa la función que se va a analizar, en Mathematica con el siguiente formato:
RootLocusPlot [tfunc, {k, k_0, k_1}]
tfunc es la función de transferencia en la variable de frecuencia s y un parámetro real k. k_0 y k_1 son el rango para el parámetro real k que se va a variar int él Root Locus Plot. Siga un ejemplo a continuación.
Ejemplo: Ecuación para hacer una Gráfica de Locus Raíz con:
\[H(s) = \drac{a + 2 s + s2}{10 + 3 a s + 4 s^2 + s^3} \nonumber \]
Para hacer una Gráfica de Locus Raíz siga el siguiente código de ejemplo:
H4 [s_, a_] := (a + 2*s + s^2)/(10 + 3*a*s + 4*s^2 + s^3)
RootLocusPlot [H4 [s, a], {a, 3, 5}]
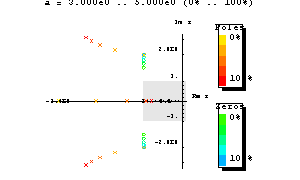Imagen: Wolfram.com
Otros formularios de Mathematica para usar RootLocusPlot []:
RootLocusPlot [func] Esta forma muestra el diagrama a polo/cero de una función es decir func sin parámetros k y k_1.
RootLocusPlot [rootloc] Esta forma muestra un locus raíz calculado con la función rootLocusByQZ [].
Consulte el enlace de Mathematica para discutir más sobre RootLocusByQZ
Se pueden variar muchas opciones para la trama, incluyendo el número de puntos, el estilo de trazado y el color de la trama. Todas estas opciones y más se pueden ver en línea con un tutorial de Mathematica
Creación de gráficas de locus raíz con Matlab
Generación de Locus Raíz en Matlab
Se han dado tres archivos matlab para obtener la gráfica de locus raíz y los polos de la gráfica de locus raíz a valores Kc especificados para una función de transferencia específica con relativa facilidad. Estos tres archivos son polesfunction.m, transferfunction.m y locusplotpoles.m. [1]. El archivo transferfunction es donde se debe ingresar la función de transferencia específica. Como está escrito, la única línea que necesita variación es la línea 4 (Gs). El archivo polesfunction encuentra los polos de la función de transferencia dada usando utilidades integradas de matlab y no necesita ninguna variación, incluso después de cambiar la función de transferencia. El archivo Locusplotpoles es lo que se llama en matlab para generar la gráfica de locus raíz así como el valor de los polos e integra los dos archivos anteriores. Para usar este archivo, escribe los valores del Kc específico para el que se requieren los valores de polo así como un único valor de Kc para el que le gustaría ver la gráfica del locus raíz. A continuación se da un ejemplo de las entradas y salidas de este archivo.
>> Locusplotpoles ([0 50 100 200] ,0)
ans =
1.0e+002 *
Columnas 1 a 3
0 -0.0020 -0.0020 + 0.0000i 0.5000 -0.0045 -0.0008 + 0.0022i 1.0000 -0.0051 -0.0004 + 0.0027i 2.0000 -0.0060 -0.0000 + 0.0034i
Columnas 4 a 6
-0.0020 - 0.0000i 0 0 -0.0008 - 0.0022i -0.0020 -0.0020 + 0.0000i -0.0004 - 0.0027i -0.0020 + 0.0000i -0.0020 - 0.0000i -0.0000 - 0.0034i -0.0020 -0.0020 + 0.0000i
Columna 7
0 -0.0020 - 0.0000i -0.0020 -0.0020 - 0.0000i
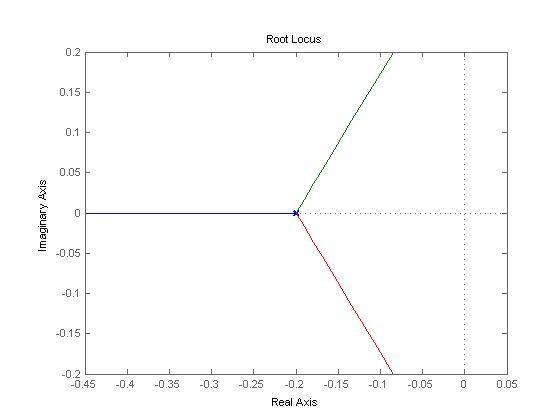
Los valores dentro de los corchetes son los valores específicos de Kc para los que se desean polos. El último valor es el Kc para el que se trazará la gráfica del locus raíz. Observe que el valor de Kc para la gráfica de locus raíz que se va a generar en este ejemplo es cero. Esto es para que toda la gama de Kc pueda ser examinada utilizando la gráfica interactiva producida por matlab. Si otras gráficas específicas de Kc quisieran ser observadas este valor se puede cambiar para generarlas también. Las líneas de columna dan los valores de entrada Kc y luego el valor de los polos para cada Kc. Tenga en cuenta que los valores reales son los valores que da matlab multiplicados por 100.
Ahora que se ha obtenido una comprensión básica de las parcelas de locus raíz, aquí hay algunos sitios web que profundizan más en los principios subyacentes y la generación de estas parcelas. www.facstaff.bucknell.edu/mastascu/econtrolhtml/rootlocus/rlocus1a.html
Este sitio ofrece ejemplos animados que progresan el valor de la variable de control a través de una gráfica de locus raíz para explicar mejor la función fundamental de estas parcelas. Sería beneficioso pasar por algunos de estos ejemplos para observar patrones de fluctuación de la variable de control. Los parámetros para cada animación se dan a la izquierda del fotograma. http://www.engin.umich.edu/group/ctm/rlocus/rlocus.html
Esta página ofrece ejemplos de cómo se genera una gráfica de locus raíz de una función de transferencia dada usando matlab. Mientras recorres el contenido de esta página, toma especial nota del hecho de que ninguna de las funciones de transferencia dadas tiene una variable Kc integrada para la cual generar una gráfica de locus. Para ver cómo se pueden generar estas gráficas cuando se especifica un valor de Kc, consulte el código de Locusplotpoles.m. Para obtener aclaraciones sobre la aplicación de parcelas de locus raíz, consulte los ejemplos dados.
Creación de gráficas de locus raíz con Excel y PPLANE
Aunque esta táctica puede seguir consumiendo un poco más de tiempo y trabajo involucrado, existe un método para computar la gráfica de Locus Raíz usando PPLAN y Excel. Este modelo en particular realmente ayuda a comprender mejor cómo leer y reconocer una Gráfica de Locus Raíz, y también es útil si actualmente no hay disponibles opciones alternativas para hacer una Gráfica de Locus Raíz.
Este método implica usar PPLAN para encontrar los valores propios para cada valor de equilibrio, y luego trazar estos puntos con el software Excel. Para ello, supongamos que tiene las siguientes ecuaciones diferenciales que representan un reactor:
\[\dfrac{dX}{dt} = -X + \dfrac{2+X+Y}{Y+3} \nonumber \]
\[\dfrac{dY}{dt} = Y \times Fin+7-(2X) \nonumber \]
Graficar las siguientes ecuaciones diferenciales proporciona algo similar a la siguiente tabla (se dibujaron algunas líneas, solo para mostrar mejor el flujo de los gráficos):
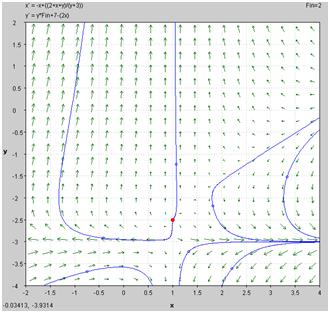
Usando la capacidad de “Encontrar un Punto de Equilibrio” en PPLANE (si necesita ayuda con PPLANE, haga clic en Análisis de PlaneFase), se puede seleccionar un punto de equilibrio particular en el campo, y ser capaz de proporcionar los siguientes resultados:
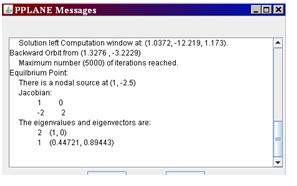
Esta ventana “aparece” en la esquina superior izquierda de la pantalla, cuando se encuentra el punto de equilibrio. Esta ventana proporciona los valores propios para este punto de equilibrio.
Dependiendo de lo que estés variando (en este caso, Fin), todo lo que tendrías que hacer es ingresar varios valores de esta Fin en PPLANE, y trazar el nuevo conjunto de fórmulas diferenciales. Una vez hecho esto, basta con encontrar el mismo punto de equilibrio, y registrar los nuevos valores propios dados en excel. Estos valores deben ingresarse con un componente x (en una columna) y un componente y (en otra columna) en excel, con las siguientes reglas:
- Suponiendo que el ejemplo 3+3i, 3-3i se dieron como valores propios.
- Para cualquier valor propio dado, el valor x de un valor propio particular es la parte real de ese número (es decir, la parte “3").
- Para cualquier punto dado, el valor y de un valor propio particular es la parte imaginaria de ese número (es decir: la parte “3i”). Si hay un componente imaginario, ignore la “i”, aunque el número debe registrarse en el componente y. Si no hay un número imaginario, el componente y es cero.
- Para ambos casos, un positivo es un positivo, y un negativo es un negativo. Recuerde: los números imaginarios tienen 2 partes, un valor de “i” positivo y negativo.
Estos puntos simplemente se registran de acuerdo con estas reglas, luego los puntos se trazan uno contra el otro, con componentes x en el eje x, y el y en el eje y. Aquí hay un ejemplo de un diagrama excel, tomado del diagrama propuesto:
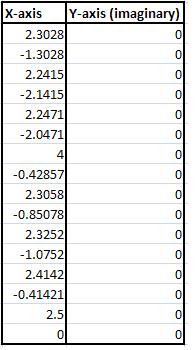
Y, entonces se trazan los datos de excel, x contra y, y se muestran a continuación:
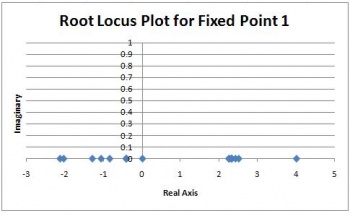
Como puede ver, este modelo en particular no tenía ningún dato imaginario. Se ha formado la gráfica de locus raíz, y para todos los relatos de Fin, los valores propios están a lo largo del eje x para la gráfica de locus raíz.
Aplicación práctica
En el pasado, era necesario que los ingenieros dominaran las técnicas necesarias para construir eficientemente diagramas de locus raíz. En el mundo actual de la ingeniería, este no es el caso por una de dos razones. En muchos casos, los diagramas de locus raíz no se utilizan industrialmente porque requieren modelos del sistema que generalmente no están disponibles. Si hay un modelo disponible para desarrollar un diagrama de locus raíz, existen aplicaciones informáticas que pueden desarrollar los diagramas mucho más rápido que una persona. Así, se debe poner energía y esfuerzo en comprender e interpretar un diagrama de locus raíz y comprender las reglas generales de estabilidad para una raíz de la ecuación característica.
Dada la siguiente tabla de raíces a la ecuación característica para un sistema:
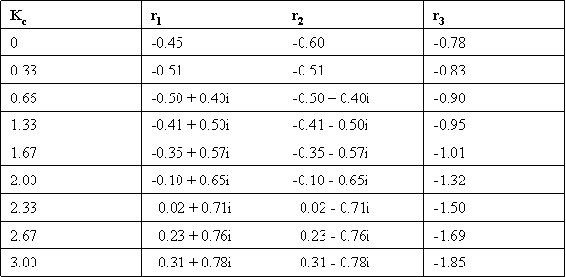
- Construir una gráfica de locus raíz (Hacer la trama a mano inicialmente puede dar a algunos una mejor comprensión de lo que está sucediendo ya que verá los cambios en la parcela a medida que agrega cada conjunto de raíces).
- Determinar los rangos de Kc que conducirían a las siguientes respuestas del sistema: sin oscilaciones, oscilaciones amortiguadas, oscilaciones estables y oscilaciones inestables. Además, esboce cómo sería la respuesta de salida para un cambio de paso dado en la entrada para cada rango de Kc.
- ¿En qué se diferenciarían las raíces de la ecuación característica si se tratara de un control de PI?
Solución
1) Parcela de locus radicular:
Primero, partimos las raíces en sus componentes imaginarios y reales:
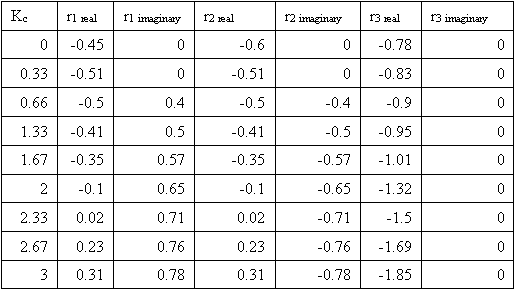
Luego, trazamos cada punto en un sistema de coordenadas complejo (eje x = componebt real, eje y = componente imaginario).
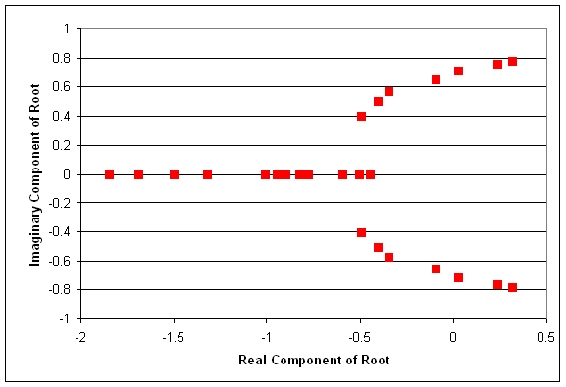
Además, es útil agregar líneas trazando el camino de Kc creciente. Estas líneas se agregan a continuación. Además, los puntos donde Kc= cero generalmente se etiquetan con una x, esto también se ha hecho en la siguiente figura.
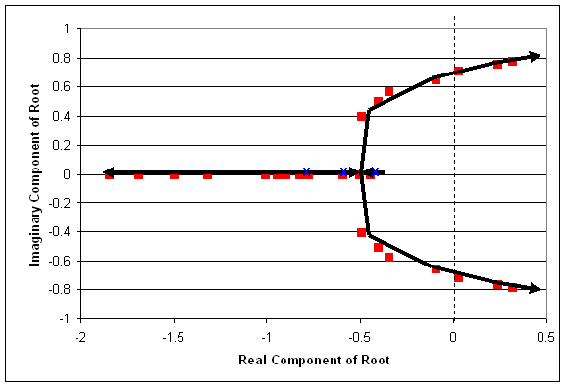
2) Rangos de Kc con explicaciones:
Sabemos que el rango donde no habrá respuesta oscilatoria es cuando Kc proporciona todas las raíces reales. Esto ocurre cuando Kc está entre 0 y 0.66. (El boceto se verá como la figura a en la sección “interpretar un diagrama de locus raíz” anterior).
Además, Kc produce oscilaciones amortiguadas cuando las dos raíces de la ecuación característica son complejas con componentes reales negativos. Esto ocurre cuando Kc es mayor que 0.66 pero menor que 2.33. (El boceto se verá como la figura b en la sección anterior “interpretar un diagrama de locus raíz”).
Las oscilaciones inestables se logran cuando dos de las raíces producen números complejos con componentes reales positivos. Esto ocurre cuando Kc es mayor a 2.33. Gráficamente, vemos que cuando los puntos se mueven más allá de la línea discontinua, tendremos oscilaciones inestables. Esto se representa en la siguiente figura. (El boceto se verá como la figura c en la sección anterior “interpretar un diagrama de locus raíz”).
Con base en los datos proporcionados, nuestra mejor suposición es que a un Kc justo por debajo de 2.33, podremos lograr oscilaciones estables. Cuando Kc = 2.33 el componente real de la raíz compleja es 0.02 (ligeramente mayor que cero). Idealmente, lograremos oscilaciones estables cuando el componente real del número complejo sea cero. (Las oscilaciones deben ser consistentes en magnitud).
Por último, es una buena idea etiquetar algunos valores de Kc en la parcela de locus raíz. Esto ayudará a orientar al lector cuando esté tratando de determinar qué punto corresponden a diferentes valores de Kc.
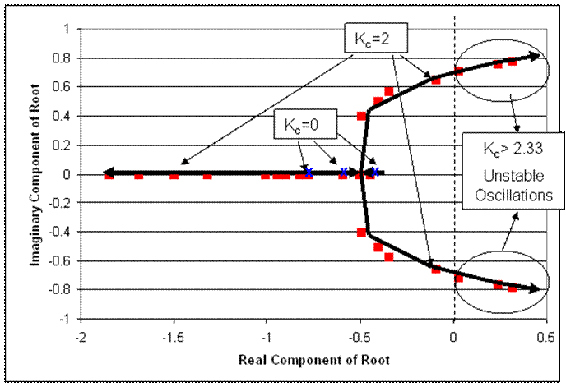
3) Si esto fuera control PI, cada raíz de la ecuación característica estaría acompañada no solo de un valor de Kc sino también de un valor para el parámetro de control integral, KI.
Te han contratado recientemente en MichChem Controls. En tu primera semana en la empresa, un virus se propaga a través de la red informática, desactivando efectivamente la mayoría de los programas computacionales. Afortunadamente, el virus se detuvo antes de que pudiera desactivar Mathematica. Poco después de que el caos del virus desaparezca, su jefe necesita saber cómo usar Mathematica para crear una gráfica de locus raíz para varios nuevos sistemas de control de nivel solo proporcional que se están probando. Siendo el ingeniero altamente calificado que eres, no quiere que pierdas el tiempo desarrollando las parcelas de locus raíz, más bien, quiere que escribas código de ejemplo, con una breve descripción que alguien más podría usar para desarrollar la gráfica de locus raíz.
La ecuación característica general para los nuevos sistemas de control de nivel es:
\[f(s) = Ax^3 + Bx^2 - Cx + D +EK_c \nonumber \]
Por favor, proporcione a su jefe un ejemplo del script exacto que necesitaría ser ingresado en Mathematica para desarrollar la gráfica del locus raíz. También deben ser breves descripciones explicando qué hace el código y qué pasos habría que repetir para desarrollar la trama.
Solución
Primero, el usuario debe desarrollar una tabla de raíces para la ecuación característica. Esto se puede hacer usando la función solve en Mathematica. El código aparecería así para Kc = 0.
(nota: el In [#] aparece por cada nueva línea de código. Esto no será escrito por el usuario.)
En [1] := Resolver [Ax^3 +Bx^2-Cx+D+E* (0) ==0, x]
Esto debe repetirse para Kc = 0.1, 0.15, 0.225, 0.5, 0.75, 1.5, etc. (hasta que las raíces de la ecuación comiencen a dar dos soluciones complejas cuyos componentes reales son positivos). Después de que se haya obtenido un número suficiente de raíces para la ecuación característica a diferentes valores de Kc, éstas deberán ser tabuladas. Para desarrollar una tabla de datos en Mathematica ingrese el siguiente código:
En [2] := A =
Callstack:
at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.06:_Parcelas_de_Locus_Raíz_-_Efecto_de_Afinación), /content/body/div[11]/div[2]/div/p[10]/span, line 1, column 12
Esto tabula los componentes reales y los componentes imaginarios en cada valor de Kc. Una vez tabulados todos los valores, la gráfica del locus raíz se puede desarrollar usando la función ListPlot.
En [3] := ListPlot [A, PlotStyle -> PointSize [0.02]
Esto representará todos los datos tabulados en In [2] que es la gráfica del locus raíz.
Ejercicio\(\PageIndex{1}\)
Se utiliza una gráfica de locus raíz para:
- Identificar las soluciones a la función de transferencia característica.
- Mostrar el tiempo de respuesta del sistema de retroalimentación a una perturbación.
- Ilustrar gráficamente el efecto de Kc sobre las características dinámicas del sistema de retroalimentación.
- Elija el Kc óptimo para el sistema de retroalimentación.
- Contestar
-
c
Ejercicio\(\PageIndex{2}\)
Cuando una raíz es compleja con partes reales positivas, las oscilaciones son:
- Disminuyendo
- Incrementando
- Inestable
- A y C
- B & C
- Contestar
-
e
Referencias
- Luyben, Michael L.; Luyben, William L. “esencial del Control de Procesos”. McGraw-Hill:Nueva York, 1997.
- Marlin, Thomas E. “Control de Procesos: Diseño de Procesos y Sistemas de Control para Rendimiento Dinámico 2da Edición”. McCgraw-Hill: Nueva York, 2000.
- Ogunnaike, Babatunde A.; Ray, W. Harmon. Dinámica de Procesos, Modelado y Control. Nueva York Oxford: Oxford UP, 1994. 488-507.
- Riggs, James B.; Karim, M. Nazmul. Control Químico y Bio-Process. 3ª ed. Ferret. 279-295.
- Luyben, Michael L.; Luyben, William L.; Tyreus, Bjorn D. “Control de procesos en toda la planta”. Mcgraw-Hill:Nueva York, 1999.
- Seborg, Dale E.; Edgar, Thomas F.; Mellichamp, Duncan A. “Dinámica y control de procesos”. John Wiley and Sons, Inc. 2004.
- http://www.engin.umich.edu/group/ctm/rlocus/rlocus.html visto 10/23/2007
- www.facstaff.bucknell.edu/mastascu/econtrolhtml/rootlocus/rlocus1a.html visto el 23/10/2007
Colaboradores y Atribuciones
- Autores: Halley Crast, Andrew Laskowski, Maurice Telesford, Emily Yatch
- Administradores: Victoria Cardine, Anthony Campell, David Hines, Stephen Kerns