12.1: Determinar si un sistema puede ser desacoplado

Última actualización
Guardar como PDF

Page ID: 85346

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Autores: Wen Chung Lim, James Bennett, Jamila Grant, Ajay Bhasin

Introducción

Un sistema de entradas y salidas puede describirse como uno de cuatro tipos: SISO (entrada única, salida única), SIMO (entrada única, salida múltiple), MISO (entrada múltiple, salida única) o MIMO (entrada múltiple, salida múltiple).

Los sistemas de múltiples entradas y múltiples salidas (MIMO) describen procesos con más de una entrada y más de una salida que requieren múltiples bucles de control. Los ejemplos de sistemas MIMO incluyen intercambiadores de calor, reactores químicos y columnas de destilación. Estos sistemas pueden complicarse a través de interacciones de bucle que dan como resultado variables con efectos inesperados. El desacoplamiento de las variables de ese sistema mejorará el control de ese proceso.

Un ejemplo de un sistema MIMO es un CSTR encamisado en el que la formación del producto depende de la temperatura del reactor y del caudal de alimentación. El proceso es controlado por dos bucles, un bucle de control de composición y un bucle de control de temperatura. Los cambios en la velocidad de alimentación se utilizan para controlar la composición del producto y los cambios en la temperatura del reactor se realizan al aumentar o disminuir la temperatura de la camisa. Sin embargo, los cambios realizados en la alimentación cambiarían la masa de reacción y, por lo tanto, la temperatura y los cambios realizados en la temperatura cambiarían la velocidad de reacción y, por lo tanto, influirían en la composición. Este es un ejemplo de interacciones de bucle. Las interacciones de bucle deben evitarse porque los cambios en un bucle podrían causar cambios desestabilizadores en otro bucle. Para evitar interacciones de bucle, los sistemas MIMO se pueden desacoplar en bucles separados conocidos como sistemas de entrada única y salida única (SISO). El desacoplamiento se puede hacer usando varias técnicas diferentes, incluyendo la reestructuración del emparejamiento de variables, la minimización de las interacciones mediante la desafinación de bucles de control conflictivos, la apertura de bucles y su puesta en control manual, y el uso de combinaciones lineales de variables manipuladas y/o controladas. Si el sistema no se puede desacoplar, entonces se deben usar otros métodos como las redes neuronales o el control predictivo de modelos para caracterizar el sistema.

Hay dos formas de ver si un sistema se puede desacoplar. Una forma es con modelos matemáticos y la otra es un método de adivinación educado más intuitivo. Los métodos matemáticos para simplificar los esquemas de control MIMO incluyen el método de matriz de ganancia relativa (RGA), el índice de Niederlinski (NI) y la descomposición de valores singulares (SVD). Este artículo discutirá la determinación de si un esquema de control MIMO puede desacoplarse a SISO usando el método SVD. También se discutirá una forma más intuitiva de desacoplar un sistema utilizando una variación del método RGA.

Definiciones de los tipos de sistemas de entrada y salida

1. SISO - Entrada Única, Salida Única

Estos sistemas utilizan datos/entrada de un sensor para controlar una salida. Estos son los más simples de diseñar ya que corresponden un sensor a un actuador. Por ejemplo, la temperatura (TC) se utiliza para controlar el estado de la válvula de v1 a través de un controlador PID.

2. SIMO - Entrada Única, Salida Múltiple

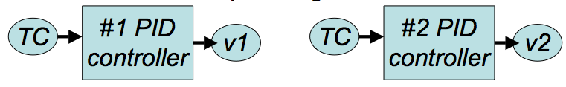
Estos sistemas utilizan datos/entrada de un sensor para controlar múltiples salidas. Por ejemplo, la temperatura (TC) se utiliza para controlar el estado de la válvula de v1 y v2 a través de controladores PID.

3. MISO - Entrada múltiple, salida única

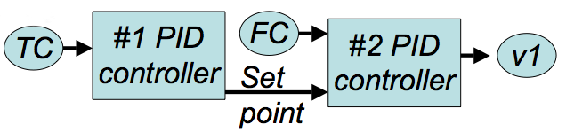
Estos sistemas utilizan datos/entrada de múltiples sensores para controlar una salida. Por ejemplo, un controlador en cascada puede considerarse MISO. La temperatura (TC) se utiliza en un controlador PID (#1) para determinar un punto de ajuste de caudal, es decir, FcSet. Con el controlador FCSet y FC, se utilizan para controlar el estado de la válvula de v1 a través de un controlador PID (#2).

4. MIMO - Entrada múltiple, salida múltiple

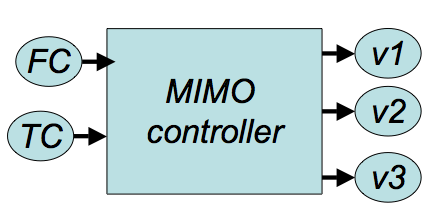
Estos sistemas utilizan datos/entradas de múltiples sensores para controlar múltiples salidas. Estos suelen ser los más difíciles de diseñar ya que los datos de múltiples sensores están integrados para coordinar múltiples actuadores. Por ejemplo, el caudal (FC) y la temperatura (TC) se utilizan para controlar múltiples válvulas (v1, v2 y v3). A menudo, los sistemas MIMO no son controladores PID sino diseñados para una situación específica.

Descomposición del Valor Singular

La descomposición de valores singulares es una forma matemática útil para determinar si un sistema será propenso a las interacciones debido a problemas de sensibilidad que resultan de pequeños errores en las ganancias del proceso. Se trata de una técnica matricial que determina si un sistema es capaz de desacoplarse.

Sistema de dos entradas y dos salidas

El método SVD comienza con la matriz de ganancia de estado estacionario, que se obtiene del método de matriz de ganancia relativa (RGA) para un sistema de bucle de control de 2 entradas y 2 salidas dado:

$[G] =\ begin {bmatrix} g_ {1,1} & g_ {1,2} \\ g_ {2,1} & g_ {2,2}\\ \ fin {bmatrix}$ ,

Usando [G], obtenemos los valores propios para el sistema. Esto se puede hacer a través de dos métodos; o bien los valores propios se pueden obtener a través de software numérico como se describe en la sección Valores propios y vectores propios o los valores propios se pueden calcular a mano. Aquí se muestran los cálculos de la mano. [G] da los siguientes valores para el sistema, los cuales se han derivado del trabajo teórico y se utilizan para encontrar los valores propios:

b = g ₁₁ ² + g ₁₂ ² — (1)
c = g ₁₁ g ₂₁ + g ₁₂ g ₂₂ — (2)
d = g ₂₁ ² + g ₂₂ ² — (3)

b, c y d son parámetros creados para este método que no tienen un significado físico directo. El uso de las fórmulas siguientes con los valores de b, c y d da los valores propios para el sistema:

λ ₁ = s ₁ ² =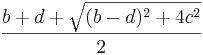 $frac {b + d +\ sqrt {(b-d) ^2+4 c^2}} {2}$ — (4)

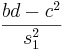λ ₂ = s ₂ ² = $frac {bd-c^2} {s_1^2}$ — (5)
s ₁ y s ₂ son las raíces cuadradas positivas de los respectivos valores propios. El número de condición CN se define como la relación entre el mayor de los dos valores y el valor más pequeño:

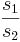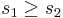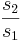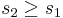
CN = $frac {s_1} {s_2}$ si $s_1}\ ge {s_2}$ , o CN = $frac {s_2} {s_1}$ si $s_2}\ ge {s_1}$

Cuanto mayor sea el valor de CN, más difícil será desacoplar el sistema en cuestión. Como regla general, es imposible desacoplar un sistema con un número CN superior a 50. Tal sistema ha manipulado variables que tienen un impacto relativo significativo y similar en las variables controladas que afectan y por lo tanto las ecuaciones de control para el sistema no pueden ser reestructuradas para obtener un sistema de control más simple. En el peor de los casos para un sistema de dos entradas y dos salidas, usar exactamente la misma variable de control dos veces daría un número CN de infinito, ya que ambas variables de control tendrían el mismo efecto sobre las variables controladas. Un sistema ideal tendría un número CN de uno, donde cada variable de control controla una única variable de salida distinta.

Sistemas MIMO con dos o más entradas y salidas

Para utilizar este método, es necesario saber cómo crear una matriz de transposición. Una matriz de transposición se crea escribiendo las columnas de la matriz original como las filas de la matriz de transposición. Matemáticamente, la matriz de transposición se denota por [A] ^T, donde [A] es la matriz original. Aquí se muestra un ejemplo: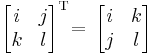 $begin {bmatrix} i & j\\ k & l\ end {bmatrix} ^ {\ mathrm {T}}\! \! \;\! =\, \ comenzar {bmatrix} i & k\\ j & l\ end {bmatrix}$

Para utilizar la descomposición de valores singulares en sistemas con dos o más entradas y salidas, la matriz de ganancia de estado estacionario m x m [G] de la forma

\[$[G]=\left[\begin{array}{cccc}g_{1,1} & g_{1,2} & \cdots & g_{1, m} \\ g_{2,1} & g_{2,2} & \cdots & g_{2, m} \\ \vdots & & & \\ g_{n, 1} & g_{n, 2} & \cdots & g_{n, m}\end{array}\right]$ \nonumber \]

se desglosa en la forma:

\[$G=U \Sigma V^{\top}$ \nonumber \]

donde:

U es una matriz m x m, cuyos vectores de columna son los vectores propios unitarios de la matriz m x m GG ^T, siendo G ^T la matriz de transposición de G.
V es una matriz m x m, cuyos vectores de columna son los vectores propios unitarios de la matriz m x m G ^T G.
σ es una matriz diagonal m x m que contiene valores singulares, donde los valores se organizan en orden descendente desde la esquina superior izquierda hasta la esquina inferior derecha.

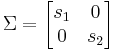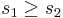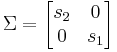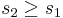$\ Sigma =\ begin {bmatrix} s_ {1} & 0 \\ 0 & s_ {2}\\ \ end {bmatrix}$ para un sistema de 2 entradas 2 salidas si $s_1}\ ge {s_2}$ , o $\ Sigma =\ begin {bmatrix} s_ {2} & 0 \\ 0 & s_ {1}\\ \ end {bmatrix}$ para un sistema de 2 entradas 2 salidas si $s_2}\ ge {s_1}$ .

El número CN puede entonces ser determinado por la relación entre el valor más grande en σ y el valor más pequeño. Observe en el ejemplo anterior de dos entradas dos salidas, no hubo necesidad de calcular la matriz de valores propios σ para una matriz de dos por dos, ya que los valores propios se pueden calcular directamente con los parámetros b, c y d.

Para obtener más información sobre cómo derivar las tres matrices U, σ y V a mano, consulte la sección Valores propios y vectores propios.

Mathematica también se puede utilizar para encontrar U, σ y V para una matriz G dada m x m Esto se logra escribiendo en el comando

Mapa [MatrixForm, {u, w, v} =SingularValueDescomposición [G]],

dando U, σ y V en ese orden.

Desacoplamiento intuitivo usando el RGA

Con esta técnica, el primer paso es construir el RGA colocando todos los controladores en manual, cambiando el valor de la salida manualmente, y luego registrando el valor final del controlador después de realizar el cambio. Esto dará la matriz de ganancia, que luego se multiplica por su inversa para dar la matriz de ganancia relativa. El objetivo aquí es emparejar mediciones y válvulas de control para que los elementos de ganancia relativa estén cerca de 1, y todas las demás combinaciones estén cerca de cero. A valores entre 0 y 1 indica que el efecto neto de los otros bucles en este emparejamiento es cambiar la señal de medición en la misma dirección que la señal de la válvula de control (cooperación). Un valor mayor a uno significa que la señal de medición irá en la dirección opuesta a la señal de la válvula de control (conflicto). Finalmente, un elemento de ganancia relativa menor a cero significa que el efecto neto es conflicto, pero aquí la ganancia cambiará de signo, no la señal de medición. Por lo tanto, si un bucle es estable cuando los otros bucles están en manual, probablemente no será estable cuando los otros bucles estén en automático, y viceversa. Para desacoplar intuitivamente este sistema, entonces se requeriría una conjetura y verificación de diferentes emparejamientos, con el objetivo de acercar los emparejamientos a un elemento de ganancia relativa a uno. Si esto no es posible y ningún emparejamiento da un valor cercano a uno, entonces el sistema necesitará ser desacoplado usando control de desacoplamiento.

Desacoplamiento de un sistema mediante control de desacoplamiento

El objetivo del control de desacoplamiento es eliminar interacciones complicadas de bucle para que un cambio en una variable de proceso no provoque cambios correspondientes en otras variables de proceso. Para ello se utiliza un esquema de control no interactuante o de desacoplamiento. En este esquema, se usa una red de compensación llamada desacoplador justo antes del proceso. Este desacoplador es el inverso de la matriz de ganancia y permite que todas las mediciones se pasen a través de él para dar un desacoplamiento completo de todos los bucles. Esto se muestra pictóricamente a continuación.

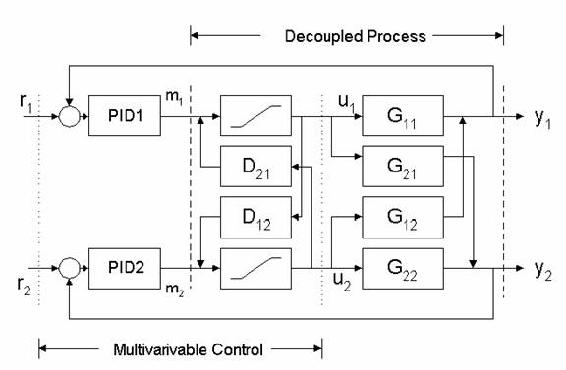
Para un ejemplo simple de reactor encamisado, si cambiar el caudal del reactivo para obtener una composición deseada también aumenta la temperatura del reactor en cinco grados, el desacoplador disminuiría la temperatura de la camisa para disminuir la temperatura dentro del reactor en cinco grados, compensando la original cambio. Esta disminución de la temperatura de la camisa también cambia la composición dentro del reactor, por lo que un controlador adecuadamente diseñado da cuenta de ambos efectos en el esquema de control para obtener la composición deseada sin cambiar la temperatura del reactor.

Funcionado Ejemplo 1

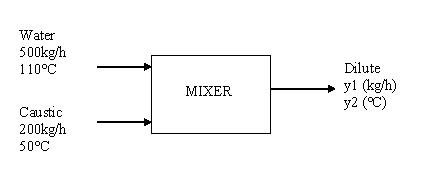
Se bombea agua caliente a 110°C a una mezcladora a 500 kg/h. El agua se utiliza para diluir una sustancia cáustica concentrada a 50°C que fluye a 200 kg/h. A continuación se muestra un diagrama del proceso. Verificar, por el método de descomposición de valores singulares, para ver si es factible el desacoplamiento del sistema. Supongamos que las capacidades de calor de ambas corrientes son las mismas sin calor de mezcla.

\[\\bold{Solution:} \nonumber \]

De la pregunta que conoces:

T ₁ = 383.15 K

T ₂ = 323.15 K

m ₁ = 500 kg/h

m ₂ = 200 kg/h

y ₁ = caudal másico saliente (kg/h)

y ₂ = temperatura de la corriente de salida (K)

De los balances de masas ya sabes:

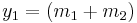
$y_1 =\ izquierda (m_1 + m_2\ derecha)$

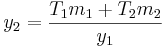
$y_2 =\ frac {t_1m_1 + T_2m_2} {y_1}$

Entonces:

y ₁ = 700 kg/h

y ₂ = 366.01 K

La matriz de ganancia de estado estacionario (G) necesita ser calculada como se explica en el método RGA:

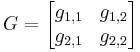
$G =\ begin {bmatrix} g_ {1,1} & g_ {1,2} \\ g_ {2,1} & g_ {2,2}\ end {bmatrix}$

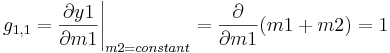
$g_ {1,1} =\ frac {\ parcial y1} {\ parcial m1}\ Bigg|_ {m2=constante} =\ frac {\ parcial} {\ m1 parcial} (m1 + m2) = 1$

$g_ {2,1} =\ frac {\ parcial y2} {\ parcial m1}\ Bigg|_ {m2=constante} =\ frac {\ parcial} {\ parcial} {\ m1 parcial}\ izquierda (\ frac {T1m1 + T2m2} {m1 + m2}\ derecha) =\ izquierda [\ frac {(T1-T2) m2} {(m1+m2) ^2}\ derecha]$

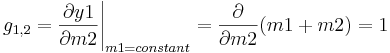
$g_ {1,2} =\ frac {\ parcial y1} {\ m2 parciales}\ Bigg|_ {m1=constante} =\ frac {\ parcial} {\ m2 parciales} (m1 + m2) = 1$

$g_ {2,2} =\ frac {\ y2 parcial} {\ m2 parciales}\ Bigg|_ {m1=constante} =\ izquierda [\ frac {(T2-T1) m1} {(m1+m2) ^2}\ derecha]$

Al conectar todos los valores conocidos, la matriz de ganancia de estado estacionario se convierte en:

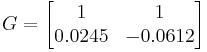
$G =\ begin {bmatrix} 1 & 1 \\ 0.0245 & -0.0612\ end {bmatrix}$

Desde aquí puedes resolver para los valores b, c, d λ ₁, λ ₂, s ₁ y s ₂ usando las ecuaciones (1) a (5) en el wiki:

b = g ₁₁ ² + g ₁₂ ² = 1 ² + 1 ² = 2

c = g ₁₁ g ₂₁ + g ₁₂ g ₂₂ = (1) (.0245) + (1) (− .0612) = -0.0367

d = g ₂₁ ² + g ₂₂ ² = .0245 ² + − .0612 ² = 0.004346

λ ₁ =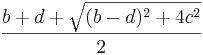 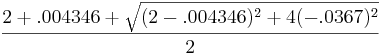$frac {b + d +\ sqrt {(b-d) ^2+4 c^2}} {2}$ = $frac {2 + .004346 +\ sqrt {(2-.004346) ^2+4 (-.0367) ^2}} {2}$ = 2

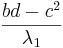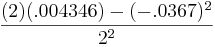λ ₂ = $frac {bd-c^2} {\ lambda_1}$ = $frac {(2) (.004346) - (-.0367) ^2} {2^2}$ = 0.003673

s ₁ =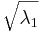 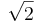$sqrt {\ lambda_1}$ = sqrt {2} = 1.414

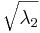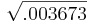s ₂ = $sqrt {\ lambda_2}$ = sqrt {.003673} = 0.0606

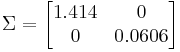
$\ Sigma =\ begin {bmatrix} 1.414 & 0 \\ 0 & 0.0606\ end {bmatrix}$

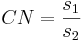$CN =\ frac {s_1} {s_2}$ = 23.33

CN es menor a 50, por lo que el desacoplamiento para este sistema es factible.

Funcionado Ejemplo 2

Un reactor encamisado con una sola corriente de alimentación (Corriente 1) es monitoreado por 3 controladores proporcionales (P) como se indica en la figura.

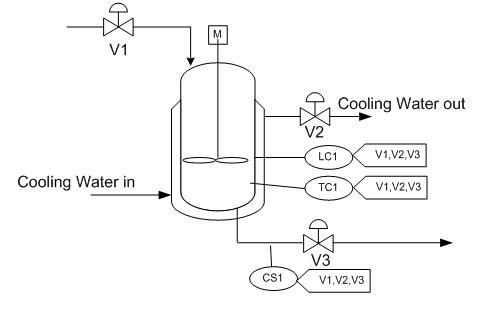
Todos estos controladores actúan como entradas a cada una de las 3 válvulas según las relaciones:

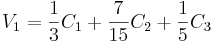
$V_1 =\ frac {1} {3} C_1+\ frac {7} {15} C_2+\ frac {1} {5} C_3$

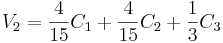
$V_2 =\ frac {4} {15} C_1+\ frac {4} {15} C_2+\ frac {1} {3} C_3$

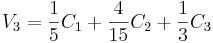
$V_3 =\ frac {1} {5} C_1+\ frac {4} {15} C_2+\ frac {1} {3} C_3$

Donde:

C ₁ = K _c ₁ e ₁ (t) + b ₁, C ₁ es la salida del controlador de nivel

C ₂ = K _c ₂ e ₂ (t) + b ₂, C ₂ es la salida del controlador de temperatura

C ₃ = K _c ₃ e ₃ (t) + b ₃, C ₃ es la salida del sensor de composición

¿Es factible desacoplar este sistema?

\[\\bold{Solution:} \nonumber \]

La matriz de ganancia se calcula de acuerdo con el método RGA y es:

Ingrese los siguientes comandos en Mathematica para el análisis SVD:

G =

ParseError: EOF expected (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/12:_Control_de_entrada_múltiple,_salida_múltiple_(MIMO)/12.01:_Determinar_si_un_sistema_puede_ser_desacoplado), /content/body/div[4]/p[16]/span, line 1, column 4

G = G*1.0 Mapa [MatrixForm, {u, w, v} =Valor SingularDescomposición [G]]

La salida de la descomposición SVD es la siguiente:

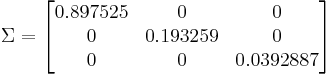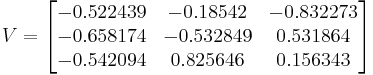
$U =\ begin {bmatrix} -0.657043 & -0.75205 & 0.052116 \\ -0.552104 & 0.432979 & -0.712538 \\ -0.513299 & 0.496941 & 0.699696\ end {bmatrix}$ , $\ Sigma =\ begin {bmatrix} 0.897525 & 0 & 0 \\ 0 & 0.193259 & 0 \\ 0 & 0 & 0.0392887\ end {bmatrix}$ , $V =\ begin {bmatrix} -0.522439 & -0.18542 & -0.832273 \\ -0.658174 & -0.532849 & 0.531864 \\ -0.542094 & 0.825646 & 0.156343\ end {bmatrix}$

El número de condición se calcula a partir de los valores más altos y más bajos de la matriz:

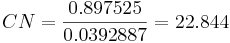
$CN =\ frac {0.897525} {0.0392887} = 22.844$

CN < 50, por lo tanto el sistema puede ser desacoplado.

Como un problema más complicado, considere cómo cambiaría este problema si los controladores usaran un estilo de control en cascada. Para un controlador P, la salida puede ser similar a:

C ₂ = K _c ₂ e ₂ (t) + b ₂ = K _c ₂ * (LC _real − f (C ₁)) + b

¿Y si usamos un controlador PID en su lugar?

Pregunta de opción múltiple 1

El CN, o condición número

a. Es la relación entre el número menor (s ₂) y el número mayor (s ₁)
b. Determina la viabilidad de desacoplar un sistema.
c. Es la unidad de vectores propios de la matriz m x m G ^T G
d. Siempre es menor que 50.

Respuesta: b

Pregunta de opción múltiple 2

Para los sistemas MIMO

a. Los bucles de control se aíslan
b. Cada variable controlada solo es manipulada por una variable
c. El desacoplamiento del sistema lo hace más complicado
d. Las variables manipuladas pueden afectar a varias variables controladas

Respuesta: d

Rincón de Sage

www.youtube.com/v/j-heeevmeam Presentación Powerpoint
Unnarated

Referencias

Mahoney, D.P., Svrcek, W.Y., y Young, B.R. (2006) A Real-Time Approach to Process Control, 2a Edición. John Wiley & Sons, Ltd. ISBN 0470025336
Gwak, K.W., Masada, G.Y. (2005) “Análisis estructural y optimización de sistemas de control no lineales mediante descomposición de valores singulares”. Sociedad Americana de Ingenieros Mecánicos Revista de Sistemas Dinámicos, Medición y Control, Vol. 127, No. 1, pp. 105-113, marzo de 2005.
McMillan, Gregory K. (1983) Afinación y Control de Loop Performance. Sociedad de Instrumentos de América. ISBN 0-87664-694-1.
Tham, M.T. (1999). “Control Multivariable: Una Introducción al Control de Desacoplamiento”. Departamento de Ingeniería Química y de Procesos, Universidad de Newcastle upon Tyne. Disponible en línea en: lorien.ncl.ac.uk/ming/mloop/mloop.pdf.
Lee, Jay H., Choi, Jin Hoon, y Lee, Kwang Soon. (1997). “3.2 Interacción y emparejamiento de E/S”. Centro de Información de Investigación en Ingeniería Química. Disponible en línea en: www.cheric.org/education/practical/mpc16473.pdf.