12.2: Control MIMO usando RGA

Última actualización
Guardar como PDF

Page ID: 85335

Angela Yeung, Ben van Kuiken, Curt Longcore, & Jeffrey Carey
University of Michigan

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

Los esquemas de control de la variable S ingle I nput o S ingle variable O utput (SISO) son solo un tipo de esquema de control que los ingenieros en la industria utilizan para controlar su proceso. También pueden usar MIMO, que es un esquema de control M ulti- I nput- M ulti- O utput. En MIMO, una o más variables manipuladas pueden afectar las interacciones de variables controladas en un bucle específico o en todos los demás bucles de control. Un esquema de control MIMO es importante en sistemas que tienen múltiples dependencias e interacciones múltiples entre diferentes variables, por ejemplo, en una columna de destilación, donde una variable manipulada como la relación de reflujo podría afectar directa o indirectamente el caudal de alimentación, la composición del producto y el energía de reboiler. Por lo tanto, comprender la dependencia de diferentes variables manipuladas y controladas en un esquema de control MIMO podría ser extremadamente útil en el diseño e implementación de un esquema de control para un proceso.

Un método para diseñar y analizar un esquema de control MIMO para un proceso en estado estacionario es con un R elativo G ain A rray (RGA). RGA es útil para sistemas MIMO que se pueden desacoplar (consulte el artículo sobre cómo determinar si un sistema puede desacoplarse). Para los sistemas que no se pueden desacoplar, el control predictivo de modelos o las redes neuronales son mejores opciones de herramienta de análisis que RGA. Un buen esquema de control MIMO para un sistema que se puede desacoplar es aquel que puede controlar una variable de proceso sin afectar mucho a las otras variables de proceso. También debe ser estable con respecto a situaciones dinámicas, cambios de carga y perturbaciones aleatorias. El RGA proporciona un enfoque cuantitativo para el análisis de las interacciones entre los controles y la salida, y así proporciona un método de emparejamiento de variables manipuladas y controladas para generar un esquema de control.

¿Qué es RGA?

R elativo G ain Un rray es una herramienta analítica utilizada para determinar los emparejamientos óptimos de variables entrada-salida para un sistema multi-input-multi-output (MIMO). En otras palabras, el RGA es una forma normalizada de la matriz de ganancia que describe el impacto de cada variable de control en la salida, en relación con el impacto de cada variable de control en otras variables. La interacción del proceso de los sistemas de control de bucle abierto y bucle cerrado se mide para todos los posibles emparejamientos de variables de entrada y salida. Se determina una relación de esta 'ganancia' de bucle abierto a esta 'ganancia' de bucle cerrado y los resultados se muestran en una matriz.

\ [R G A=\ lambda=\ left [\ begin {array} {cccc}
\ lambda_ {11} &\ lambda_ {12} &\ cdots &\ lambda_ {1 n}\
\\ lambda_ {21} &\ lambda_ {22} &\ cdots &\ lambda_ {2 n}\
\\ vdots & &\
\ lambda_ {n 1} &\ lambda_ {n 2} &\ cdots & amp;\ lambda_ {n n}
\ end {array}\ derecha]\ nonumber\]

La matriz será una matriz con una columna por cada variable de entrada y una fila por cada variable de salida en el sistema MIMO. Este formato permite a un ingeniero de procesos comparar fácilmente las ganancias relativas asociadas con cada par de variables de entrada y salida y, en última instancia, hacer coincidir las variables de entrada y salida que tienen el mayor efecto entre sí al tiempo que minimiza los efectos secundarios no deseados.

Comprensión de los resultados de la RGA

Cuanto más cerca están los valores en el RGA a 1, más desacoplado está el sistema
El valor máximo en cada fila del RGA determina qué variables deben acoplarse o vincularse
También cada fila y cada columna deben sumar a 1

Ejemplo

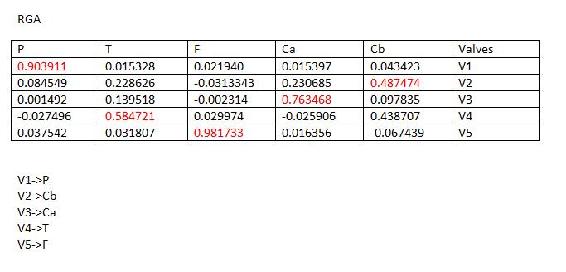
La siguiente tabla incluye los resultados de RGA. Los valores resaltados en rojo son los valores máximos en la fila. Estos valores indicaron que la válvula para esa fila debe ser utilizada para controlar la variable que aparece listada en la columna correspondiente.

Cálculo de RGA

Hay dos formas principales de calcular RGA:

Determinar experimentalmente el efecto de las variables de entrada sobre las variables de salida, luego compilar los resultados en una matriz RGA.
Utilice una matriz de ganancia en estado estacionario para calcular la matriz RGA.

Se debe utilizar el método (1) cuando sea posible llevar a cabo los experimentos como se detalla en la sección Cálculo de RGA con Experimentos. Este método generalmente producirá la matriz RGA más precisa del sistema porque se basa en datos reales tomados del sistema de control operativo. Si no es posible realizar estos extensos experimentos, se puede utilizar el método (2). Si se dispone de un modelo de proceso, se puede utilizar el método (2) sin datos experimentales. Si no hay un modelo de proceso disponible, se deben tomar algunos datos experimentales (aunque menos extensamente que en el método (1)) y usarse junto con el método (2).

Método 1: Cálculo de RGA con Experimentos

Este método de cálculo del RGA se puede utilizar cuando es posible ejecutar experimentos en cada uno de los emparejamientos entrada-salida. A continuación se muestra una explicación paso a paso de cómo compilar experimentalmente el RGA para un sistema MIMO simple.

El sistema MIMO más simple es aquel que tiene dos entradas y dos salidas. Recuerda que por definición, un cambio en una de las entradas en un sistema MIMO cambiará ambas salidas. Este sistema se puede expresar matemáticamente como se escribe a continuación.

\[y_1 = a_{11}m_1 + a_{12}m_2 \nonumber \]

\[y_2 = a_{21}m_1 + a_{22}m_2 \nonumber \]

Donde y _i es la salida para el bucle i, las m variables son las entradas para cada bucle, y las variables a son las funciones de transferencia. También ayuda ver este sistema como un diagrama de control, como se muestra aquí.

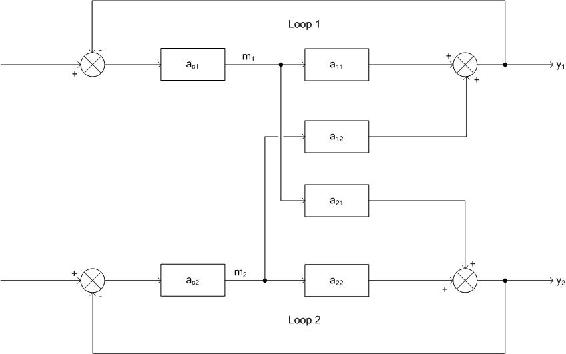
iki 3 pic.jpg

Claramente, tanto y ₁ como y ₂ se ven afectados por ambas entradas (m ₁ y m ₂). Debido a esto, hay dos opciones para el control. y ₁ podría ser controlado por m ₁, o y ₁ podría ser controlado por m ₂. y ₂ sería entonces controlado por la entrada que no está controlando y ₁. Para un sistema MIMO con n variables de entrada, hay n! posibles configuraciones de control. La pregunta es: ¿Qué configuración te dará el mejor control? La respuesta se puede determinar encontrando la matriz de ganancia relativa (RGA). Existen algunas formas de determinar el RGA, una de las cuales es haciendo dos experimentos, repetidos para cada configuración posible. El RGA se puede ensamblar a partir de los datos recopilados. Estos experimentos se explican a continuación utilizando el dibujo anterior y la configuración donde m ₁ controla y ₁.

Experimento 1

Para el primer experimento, el objetivo es observar el efecto de m ₁ sobre y ₁. Para ello, todos los bucles deben estar abiertos. En otras palabras, se elimina el bucle de retroalimentación y el sistema se ejecuta manualmente sin control. Esta configuración se muestra a continuación.

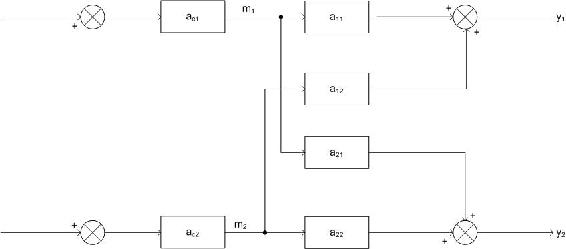
iki 3 pic2.jpg

Ahora, dado que el sistema está bajo control manual, es posible introducir un cambio de paso Δ m ₁ manteniendo constante m ₂. Debido a que m ₂ se mantiene constante, el cambio en y ₁, Δ y ₁, puede atribuirse enteramente a m ₁. Si bien un cambio en m ₁ también afectará a y ₂, es la relación entre m ₁ e y ₁ la que debe observarse en este punto. Entonces, la ganancia de y ₁ con respecto a m ₁ con todos los bucles abiertos se define como g ₁₁. A continuación se muestra el cálculo de g ₁₁.

\[g_{11}=\frac{\Delta y_{1}(\text { all - loops -open })}{\Delta m_{1}(\text { all }-\text { loops -open })} \nonumber \]

El objetivo final del experimento uno es obtener el valor g _ij donde la variable controlada i es controlada por la variable manipulada j.

Experimento 2

El objetivo del experimento dos es determinar el efecto de m ₂ sobre y ₁. Para ello, el bucle 1 debe permanecer abierto, pero todos los demás bucles permanecen cerrados. Esta configuración se muestra a continuación.

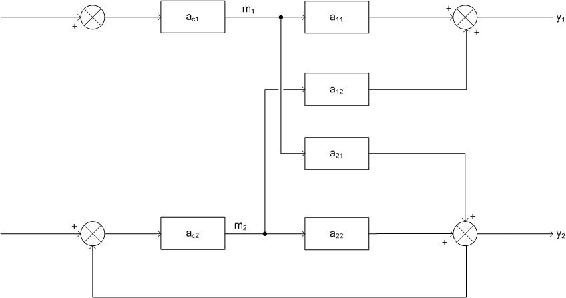
iki 3 pic3.jpg

Ahora, el mismo cambio de paso que se introdujo a m ₁ en el experimento uno debe ser introducido nuevamente. La diferencia es, ahora el bucle 2 está en perfecto control lo que significa que cuando m ₁ cambia, afecta a y ₂, por lo que el bucle de control en el bucle dos ajustará m ₂ para compensar y mantener y ₂ constante. Cuando m ₂ lo cambia, a su vez, afecta a y ₁. Es este cambio el que se está observando. La cantidad y ₁ cambios es Δ y ₁ y la cantidad m ₁ que se intensificó es Δ m ₁. Ahora:

\[g_{11}^{*}=\frac{\Delta y_{1}(\text { only }-\text { loop }-\text { one }-\text { open })}{\Delta m_{1}(\text { only }-\text { loop }-\text { one }-\text { open })} \nonumber \]

El objetivo del experimento dos es obtener este valor de$g_{i j}^{*}$ donde la variable controlada i está siendo controlada por j manipulada.

Compilando la matriz

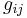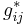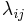Una vez que se ejecutan los experimentos para cada configuración posible, los resultados se pueden usar para compilar la matriz de ganancia relativa (RGA). Para ello, primero tenemos que encontrar la ganancia relativa. La ganancia relativa es la relación de $g_ {ij}$ a $g ^*_ {ij}$ y está representada por $\ lambda_ {ij}$ .

\[\lambda_{i j}=\frac{g_{i j}}{g_{i j}^{*}}=\frac{\left(\frac{\delta y_{i}}{\delta m_{j}}\right)_{\text {all-loops-open }}}{\left(\frac{\delta y_{i}}{\delta m_{j}}\right)_{\text {only-loop-i-open }}}\]

El valor de λ debe calcularse para cada combinación posible de i y j. Después de encontrar cada valor, se puede formar la matriz RGA:

Método 2: Cálculo de RGA con Matriz de Ganancia de Estado Estacionario

En ocasiones no es conveniente o posible realizar los experimentos descritos anteriormente en cada posibilidad de emparejamiento de control en el sistema. Si ese es el caso, se puede usar una matriz de ganancia de estado estacionario para determinar el RGA. Si hay un modelo de proceso disponible, la matriz de ganancia de estado estacionario se puede calcular a partir de las ecuaciones del modelo. Si no se dispone de un modelo de proceso, la matriz de ganancia en estado estacionario se puede calcular a partir de datos experimentales (se requieren menos experimentos que cuando el RGA se calcula directamente a partir de los datos experimentales como anteriormente). Una vez que se calcula la matriz de ganancia en estado estacionario, se puede usar para calcular el RGA. Tenga en cuenta que un RGA tiene que tener el mismo número de variables controladas y variables manipuladas (mismo número de entradas y salidas) para estar en forma de matriz m x m.

Modelo de proceso disponible

Si se dispone de un modelo de proceso, la matriz de ganancia de estado estacionario relaciona las variables manipuladas con las variables controladas de acuerdo con la siguiente ecuación:

\[\mathbf{y}=G \mathbf{m} \nonumber \]

donde$\mathbf{y}$ es un vector de las variables controladas:

\ [\ mathbf {y} =\ left [\ begin {array} {c}
y_ {1}\\
y_ {2}\\
\ vdots\\
y_ {n}
\ end {array}\ derecha]\ nonumber\]

$\mathbf{m}$es un vector de las variables manipuladas:

\ [\ mathbf {m} =\ left [\ begin {array} {c}
m_ {1}\\
m_ {2}\\
\ vdots\\
m_ {n}
\ end {array}\ derecha]\ nonumber\]

y G es la matriz de ganancia en estado estacionario:

\ [G=\ left [\ begin {array} {cccc}
g_ {11} & g_ {12} &\ cdots & g_ {1 n}\\
g_ {21} & g_ {22} &\ cdots & g_ {2 n}
\\ vdots & &\\
g_ {n 1} & g_ {n 2} &\ cdots & g_ {n}
\ end {array}\ derecha]\ nonumber\]

Los valores de g _ij se calculan tomando derivadas parciales de las ecuaciones que rigen las variables controladas. Específicamente:

\[g_{i j}=\frac{\partial y_{i}}{\partial m_{j}} \nonumber \]

Durante la diferenciación, mantener constantes todas las variables manipuladas distintas de m _j. Para rellenar la matriz G con valores numéricos, simplemente sustituya los valores de estado estacionario apropiados para el proceso en las expresiones derivadas de la diferenciación.

Ahora que se ha encontrado la matriz de ganancia en estado estacionario, el RGA se puede calcular con solo un poco más de matemáticas. Sin embargo, ahora que tiene la matriz de ganancia de estado estacionario, este podría ser un buen momento para determinar si su sistema puede incluso ser desacoplado. Consulte el artículo sobre descomposición de valores singulares para conocer los métodos para verificar esto. Suponiendo que SVD da un número de condición inferior a aproximadamente 50, podemos proceder al cálculo del RGA. Primero, defina una matriz R para que sea la transposición de la inversa de la matriz G:

\[R=\left(G^{-1}\right)^{\mathrm{T}} \nonumber \]

El cálculo de la inversa de una matriz es bastante complicado para cualquier cosa mayor que una matriz 2x2. Afortunadamente Mathematica hará esto con el siguiente comando para una matriz cuadrada M:

Inverso [M]

La transposición de una matriz es cuando las filas se convierten en columnas y las columnas se convierten en filas. Para una matriz cuadrada, esto solo significa reflejar a través de la diagonal que va desde la esquina superior izquierda hasta la esquina inferior derecha de la matriz. La transposición se puede encontrar en Mathematica con el siguiente comando:

Transpone [M]

El RGA ahora se puede obtener un elemento a la vez de acuerdo con esta ecuación:

\[\lambda_{i j}=g_{i j} r_{i j} \nonumber \]

¡Ten en cuenta que esta no es tu multiplicación matricial habitual! Aquí se multiplican los elementos correspondientes de las matrices G y R para obtener el elemento correspondiente de la RGA. Este es el tipo de multiplicación que Mathematica hace con el operador de multiplicación estándar.

Consulte el Ejemplo 1 a continuación para obtener un cálculo de RGA elaborado utilizando este enfoque.

Modelo de proceso no disponible

En caso de que no haya un modelo de proceso disponible y no sea factible determinar el RGA mediante la realización de ambos experimentos necesarios para la determinación experimental completa, aún puede ser posible desarrollar experimentalmente una matriz de ganancia en estado estacionario que luego pueda ser utilizada para derivar la RGA. En este caso, simplemente realice el experimento 1 como se describió anteriormente para determinar los elementos de la matriz de ganancia en estado estacionario:

\[g_{i j}=\frac{\Delta y_{i}}{\Delta m_{j}} \nonumber \]

con todos los bucles abiertos.

Cada elemento de la matriz de ganancia de estado estacionario se puede determinar de esta manera, y luego el RGA se puede calcular a partir de la matriz de ganancia de estado estacionario como se muestra en la sección anterior.

Interpretación de la RGA

Existen algunas propiedades y pautas importantes en la comprensión y análisis de la RGA, y qué significan los diferentes valores de la RGA:

1) Todos los elementos del RGA a través de cualquier fila, o hacia abajo en cualquier columna, sumarán hasta uno:

\[\sum_{i=1}^{n} \lambda_{i j}=\sum_{j=1}^{n} \lambda_{i j}=1 \nonumber \]

Esto facilita el cálculo del RGA porque:

en el caso 2X2, solo se debe calcular 1 elemento para determinar todos los elementos
en el caso 3X3, solo se deben calcular 4 elementos para determinar todos los elementos

y así sucesivamente.

2) La λ _ij calculada a partir de la matriz de estado estacionario es adimensional y no se ve afectada por el escalado.

3) Cada una de las filas en el RGA representa una de las salidas. Cada una de las columnas representa una variable manipulada.

Si λ _ij = 0: La variable manipulada (m _j) no tendrá ningún efecto sobre la salida o la variable controlada (y _i).
Si λ _ij = 1: La variable manipulada m _j afecta a la salida y _i sin ninguna interacción de los otros bucles de control en el sistema. De la definición de λ _ij, esto implica que el bucle de ganancia con todos los bucles abiertos es igual al bucle de ganancia con todos los demás bucles cerrados, es decir: g ₁₁ = g ^* ₁₁.
Si λ _ij < 0: El sistema será inestable siempre que m _j esté emparejado con y _i, y la respuesta opuesta en el sistema real puede ocurrir si se abren otros bucles en el sistema.
Si 0 < λ _ij < 1: Esto implica que otros bucles de control (m _j - y _i) están interactuando con el bucle de control de la variable manipulada y controlada.

Tres relaciones diferentes basadas en λ=0.5 implican diferentes interpretaciones del emparejamiento y el RGA:

Si λ _ij = 0.5: El efecto de emparejamiento de control es igual al efecto de represalia de otros bucles.
Si λ _ij < 0.5: Los otros bucles de control están influyendo en el par de control, y la influencia de los otros bucles de control es mayor que la influencia del par de control.
Si λ _ij > 0.5: Esto significa que el par de control tiene una mayor influencia en el sistema que los otros bucles de control.
Si λ _ij >1: La ganancia de bucle abierto del par de control es mayor que la ganancia con todos los demás bucles cerrados, es decir: g ₁₁ > g ^* ₁₁. El valor positivo de RGA indica que el par de control es dominante en el sistema, pero los otros bucles siguen afectando al par de control en la dirección opuesta. Cuanto mayor sea el valor de λ _ij, más efectos correccionales tendrán los otros bucles de control sobre el par.

λ _ij	Posible Emparejamiento
λ _ij = 0	Evitar emparejar m _j con y _i
λ _ij = 1	Emparejar m _j con y _i
λ _ij < 0	Evitar emparejar m _j con y _i
λ _ij = o < 0.5	Evitar emparejar m _j con y _i
λ _ij >1	Emparejar m _j con y _i

Análisis con RGA

El Índice de Niederlinski (NI) es un cálculo utilizado para analizar la estabilidad de los emparejamientos de bucles de control utilizando el resultado del RGA, evaluado en estado estacionario:

\[N I=\frac{|G|}{\prod_{i=1}^{n} g_{i i}} \nonumber \]

Un valor de NI negativo indica inestabilidad en el bucle de control. Para una matriz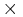 tiempos 2 2, un valor de NI positivo indica estabilidad en los emparejamientos, ¡pero esto no es necesariamente cierto para matrices más grandes! Para matrices mayores a 2 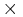tiempos 2, solo se puede extraer una conclusión de un NI negativo, lo que indica inestabilidad. NI no se debe usar para sistemas que tienen retardos de tiempo (tiempo muerto), ya que las predicciones de estabilidad de NI asumen retroalimentación inmediata al controlador. Sin embargo, el índice puede adaptarse para sistemas con tiempo muerto, aunque esa aplicación está fuera del alcance de este artículo.

Aquí hay un ejemplo de cálculo de NI: dada la matriz de ganancia de estado estacionario

\ [G=\ left [\ begin {array} {cc}
-0.002 & 0.001\\
0.002 & 0.003
\ end {array}\ derecha]\ nonumber\]

el NI se puede calcular a partir de la siguiente expresión:

\[N I=\frac{(-0.002 \times 0.003)-(0.001 \times 0.002)}{-0.002 \times 0.003}=1.333 \nonumber \]

Dado que esta es una matriz tiempos 2 2, el valor positivo del NI indica estabilidad en los emparejamientos de bucle de control.

Optimización de un esquema de control MIMO: reglas de emparejamiento

El objetivo del análisis RGA e NI es determinar cuantitativamente el emparejamiento óptimo de variables para un proceso dado. Algunas reglas básicas para recordar al intentar obtener un emparejamiento óptimo de bucles de control en un sistema son:

Regla 1: Los elementos RGA positivos más cercanos a 1.0 deben tener emparejadas las variables manipuladas y controladas correspondientes. Cuando el número CN es grande, lo que implica un sistema menos desacoplado, se deben buscar los elementos RGA máximos.
Regla 2: Si el valor de NI es negativo, el emparejamiento de bucles para esa configuración del sistema de control es inaceptable.

Ejemplo$\PageIndex{1}$

Se utiliza una unidad de mezcla para diluir y enfriar la corriente de producto de un reactor. En el mezclador se combinan tres corrientes: la corriente concentrada caliente del reactor, una corriente a temperatura ambiente que no contiene nada del producto A y una segunda corriente a temperatura ambiente que contiene algo de A producida en otra parte del proceso. Se desea controlar el caudal, la temperatura y la concentración de A en la corriente de producto manipulando los caudales de las tres corrientes de entrada. A continuación se presenta un esquema del proceso, rellenado con los valores de estado estacionario de caudal, temperatura y concentración. Las variables manipuladas se indican con la letra m y las variables controladas se indican con la letra y:

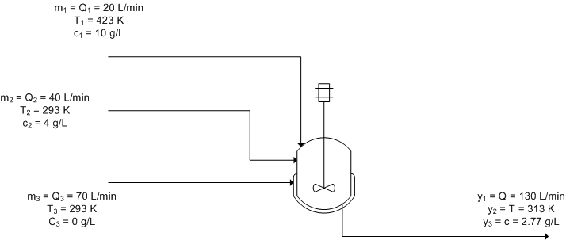
xample 1 Diagram.gif

Las ecuaciones utilizadas para modelar el sistema son:

\[y_{1}=m_{1}+m_{2}+m_{3} \nonumber \]

\[y_{2}=\frac{T_{1} m_{1}+T_{2} m_{2}+T_{3} m_{3}}{y_{1}}=\frac{T_{1} m_{1}+T_{2} m_{2}+T_{3} m_{3}}{m_{1}+m_{2}+m_{3}} \nonumber \]

\[y_{3}=\frac{c_{1} m_{1}+c_{2} m_{2}+c_{3} m_{3}}{y_{1}}=\frac{c_{1} m_{1}+c_{2} m_{2}+c_{3} m_{3}}{m_{1}+m_{2}+m_{3}} \nonumber \]

Calcule el RGA utilizando el método de matriz de ganancia en estado estacionario y utilízelo para determinar el mejor esquema de control para el sistema.

Solución

Primero debes tomar las derivadas parciales de las ecuaciones de variables de control para determinar los elementos de la matriz de ganancia en estado estacionario:

\[g_{11}=\frac{\partial y_{1}}{\partial m_{1}}=1 \nonumber \]

\[g_{21}=\frac{\partial y_{2}}{\partial m_{1}}=\frac{\left(T_{1}-T_{2}\right) m_{2}+\left(T_{1}-T_{3}\right) m_{3}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

\[g_{31}=\frac{\partial y_{3}}{\partial m_{1}}=\frac{\left(c_{1}-c_{2}\right) m_{2}+\left(c_{1}-c_{3}\right) m_{3}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

\[g_{12}=\frac{\partial y_{1}}{\partial m_{2}}=1 \nonumber \]

\[g_{22}=\frac{\partial y_{2}}{\partial m_{2}}=\frac{\left(T_{2}-T_{1}\right) m_{1}+\left(T_{2}-T_{3}\right) m_{3}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

\[g_{32}=\frac{\partial y_{3}}{\partial m_{2}}=\frac{\left(c_{2}-c_{1}\right) m_{1}+\left(c_{2}-c_{3}\right) m_{3}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

\[g_{13}=\frac{\partial y_{1}}{\partial m_{3}}=1 \nonumber \]

\[g_{23}=\frac{\partial y_{2}}{\partial m_{3}}=\frac{\left(T_{3}-T_{1}\right) m_{1}+\left(T_{3}-T_{2}\right) m_{2}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

\[g_{33}=\frac{\partial y_{3}}{\partial m_{3}}=\frac{\left(c_{3}-c_{1}\right) m_{1}+\left(c_{3}-c_{2}\right) m_{2}}{\left(m_{1}+m_{2}+m_{3}\right)^{2}} \nonumber \]

Ahora puedes sustituir en el estado estacionario dado los valores de las variables para encontrar los valores numéricos de g _ij, obteniendo:

$_ {11} =1\,$

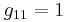
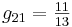
$_ {21} =\ textstyle\ frac {11} {13}$

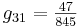
$_ {31} =\ textstyle\ frac {47} {845}$

$_ {12} =1\,$

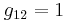
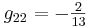
$_ {22} =\ textstyle -\ frac {2} {13}$

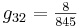
$_ {32} =\ textstyle\ frac {8} {845}$

$_ {13} =1\,$

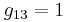
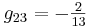
$_ {23} =\ textstyle -\ frac {2} {13}$

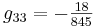
$_ {33} =\ textstyle -\ frac {18} {845}$

En forma de matriz:

\ [G=\ left [\ begin {array} {ccc}
1 & 1 & 1\
\ frac {11} {13} & -\ frac {2} {13} & -\ frac {2} {13}\
\ frac {47} {845} &\ frac {8} {845} & -\ frac {18} {845}
\ end {array}\ derecha]\ nonumber\]

Ahora calcula la matriz R:

\ [R=\ izquierda (G^ {-1}\ derecha) ^ {\ mathrm {T}} =\ izquierda [\ begin {array} {ccc}
\ frac {2} {13} &\ frac {4} {13} &\ frac {7} {13}\
1 & -\ frac {5} {2} &\ frac {3} {2}\
0 &\ frac {65} {2} & -\ frac {65} {2}
\ end {array}\ derecha]\ nonumber\]

Ahora puede calcular el RGA multiplicando las matrices G y R por partes, de acuerdo con la fórmula:

\[\lambda_{i j}=g_{i j} r_{i j} \nonumber \]

Entonces el RGA es:

\ [RGA=\ left [\ begin {array} {ccc}
\ frac {2} {13} &\ frac {4} {13} &\ frac {7} {13}\
\ frac {11} {13} &\ frac {5} {13} & -\ frac {3} {13} {13}\
0 &\ frac {4} {13} &\ frac {9} {13}
\ end {array}\ derecha]\ nonumber\]

Tenga en cuenta que todas las filas y columnas suman 1, como deberían.

Ahora es el momento de determinar el esquema de control óptimo para el sistema. Cuanto más cerca esté un elemento en la matriz de 1, mejor será el emparejamiento entre las variables manipuladas y controladas representadas por ese elemento. Con esto en mente, podemos ver de inmediato que m ₁, el caudal de la corriente 1, debe usarse para controlar y ₂, la temperatura de la corriente de salida, debido a que el valor de λ ₂₁ es el más cercano a 1 en la matriz (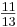 $textstyle\ frac {11} {13}$ ). El siguiente en línea es λ ₃₃, con un valor de 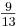$textstyle\ frac {9} {13}$ . Esto indica que m ₃, el caudal de la corriente 3, debe controlar y ₃, la concentración de A en la corriente de producto. Hasta el momento tan bueno, pero ¿qué debería controlar y ₁, el caudal del flujo del producto? La mejor opción sería m ₃, pero esto ya está controlando la concentración de A en el producto, por lo que la siguiente mejor opción es m ₂, el caudal de la corriente 2. Esto no es óptimo porque la ganancia relativa es inferior a 0.5, pero es la mejor opción disponible dadas las restricciones del sistema.

Ejemplo$\PageIndex{2}$

En una columna de destilación, se utilizan la velocidad de reflujo (R) y la velocidad de vapor (S) para controlar las composiciones en el destilado (x _D) y el producto de fondo (x _B). Los bucles de control se abren con el fin de llevar a cabo el experimento uno como se ha descrito anteriormente, y se recoge el siguiente conjunto de datos:

Juicio	R (kg/min)	S (kg/min)	x _D	x _B
1	75	20	0.96	0.05
2	85	20	0.94	0.06
3	95	20	0.92	0.08
4	85	15	0.95	0.06
5	85	25	0.97	0.03

Calcular el RGA para este sistema, y determinar cuál es el mejor emparejamiento entre las variables manipuladas (R y S) y controladas (x _D y x _B).

Solución

A partir de los datos del experimento, se observa que las velocidades de reflujo (R) son constantes para los ensayos 2, 4 y 5, mientras que las velocidades de vapor (S) son constantes para los ensayos 1, 2 y 3.
Primero, calcule la matriz de ganancia en estado estacionario para este sistema:

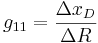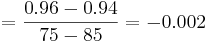
$_ {11} =\ frac {\ Delta x_d} {\ Delta R}$ con constante S $\ frac {0.96-0.94} {75-85} = -0.002$

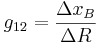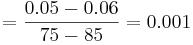
$_ {12} =\ frac {\ Delta x_b} {\ Delta R}$ con constante S $\ frac {0.05-0.06} {75-85} = 0.001$

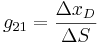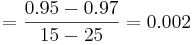
$_ {21} =\ frac {\ Delta x_d} {\ Delta S}$ con constante R $\ frac {0.95-0.97} {15-25} = 0.002$

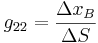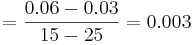
$_ {22} =\ frac {\ Delta x_b} {\ Delta S}$ con constante R $\ frac {0.06-0.03} {15-25} = 0.003$

Organice el valor de ganancia en la forma de matriz y calcule$R$:

\ [G=\ left [\ begin {array} {cc}
-0.002 & 0.001\\
0.002 & 0.003
\ end {array}\ derecha]\ nonumber\]

\ [R=\ left (G^ {-1}\ right) ^ {T} =\ left [\ begin {array} {cc}
-375 & 250\\
125 & 250
\ end {array}\ right. \ nonumber\]

Multiplique cada valor en la matriz R por su valor de ganancia correspondiente para obtener λ _ij:

\[\lambda_{11}=g_{11} R_{11} \nonumber \]

$λ_{ij}$luego se organiza en la forma de matriz RGA:

\ [R G A=\ left [\ begin {array} {cc}
\ frac {3} {4} &\ frac {1} {4}\
\ frac {1} {4} &\ frac {3} {4}
\ end {array}\ derecha]\ nonumber\]

La matriz RGA indica que la composición del destilado (x _D) estaría mejor controlada por el flujo de reflujo (R); mientras que x _B se controlaría mejor por la velocidad de vapor (S) del calderín.

Ejemplo$\PageIndex{3}$

Un problema de ejemplo basado en el segundo examen de otoño de 2008:

“Imagínese que está desarrollando un esquema de control para un nuevo sistema de reactores de baja temperatura. La física que gobierna el sistema es complicada, por lo que decides comenzar con un experimento en el sistema para ver si puedes desarrollar un conjunto simple si controladores SISO. Para evaluar esta posibilidad, comienzas con tus cinco válvulas en sus condiciones de operación en estado estacionario (v1=0.5, v2=0.55, v3=0.5, v4=0.6, v5=0.4) y mide las cinco variables clave de este proceso T1, T2, T3, P1 y P2. A continuación ajusta ligeramente cada válvula para ver los efectos de estado estacionario en cada variable de salida”

Como aproximación, ajusta este modelo al siguiente sistema:

\ [\ left [\ begin {array} {c}
T_ {1}\\
T_ {2}\\
T_ {3}\\
P_ {1}\
P_ {2}
\ end {array}\ derecha] =\ izquierda [\ begin {array} {ccccc}
-0.2 & 0.06 & 0.03 & 1.0 & 0.02\\
0.01 & 0.1 & -0.143 & amp; 0.012 & 1.0\\
0.5 & 1.0 & -0.23 & 0.04 & 0.02\\
-0.2 & -0.1 & 1.0 & 0.123 & -0.023\\
1.0 & -0.01 & 0.1 & 0.01556 & -0.013
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
\ mathrm {V} _ { 1}\\
\ mathrm {v} _ {2}\
\\ mathrm {v} _ {3}\
\ mathrm {v} _ {4}\
\ mathrm {v} _ {5}
\ end {array}\ derecha]\ nonumber\]

“Realizar un análisis RGA para encontrar el mejor emparejamiento entre válvulas (v1, v2, v3, v4 y v5) y salidas (T1, T2, T3, P1 y P2)”.

En Mathematica, puede ingresar la matriz de coeficientes de la siguiente manera:

Nota: Asigno la matriz de coeficientes a la variable, G.

Se puede ver en forma de matriz en Mathematica usando la función, “MatrixForm []”:

Con la matriz de ganancia, G, puede usar la descomposición de valores singulares (SVD) de la matriz de ganancia para determinar qué tan linealmente dependiente es el modelo. La linealidad se basa en el número de condición (CN). Mathematica tiene una función incorporada para hacer descomposición de valores singulares. A continuación se muestra cómo hacer descomposición de valores singulares para este ejemplo.

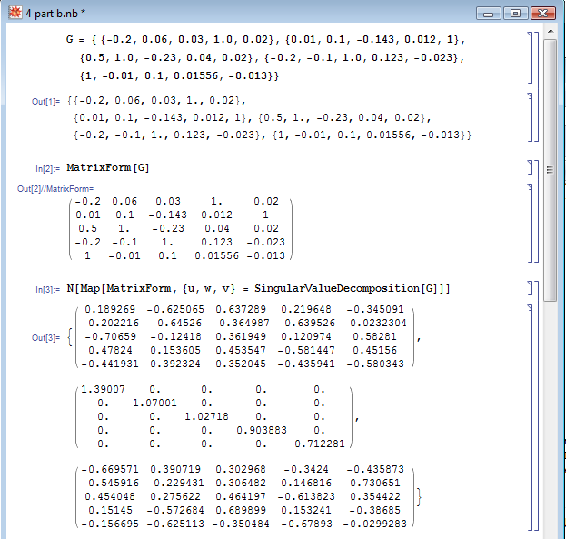
La sintaxis de Mathematica es: N [Map [MatrixForm, {u, w, v} = SingularValueDescomposición [G]]]. El “SingularValueDescomposición []” saca tres matrices asignadas a las variables u, w y v. La porción “Map [MatrixForm,...” saca las tres matrices en una vista de matriz y la porción “N [..” fuerza los valores numéricos en las matrices.

Al número de condición (CN), se divide el valor más grande por el valor más pequeño en la matriz, w. La regla general es que si el número de condición (CN) es mayor que 50, entonces el sistema/modelo es demasiado difícil de desacoplar.

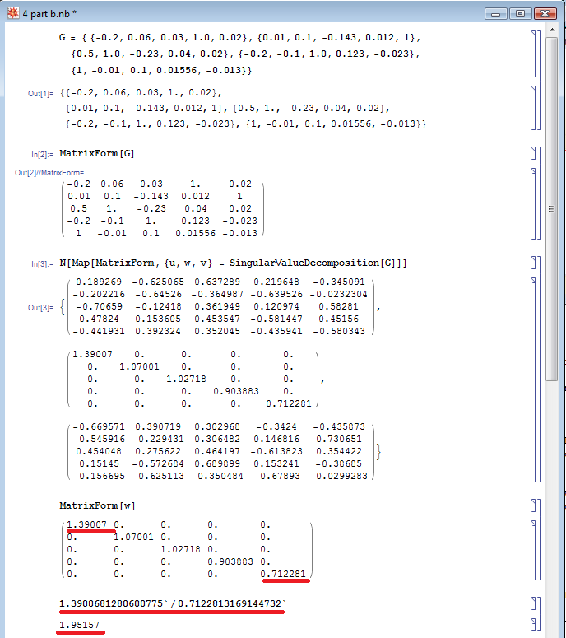
Esto ilustra que este sistema puede desacoplarse porque el número CN está por debajo de 50. Para determinar el mejor emparejamiento, se utiliza el análisis RGA en el que es una forma normalizada de la matriz de ganancia, “G” que determina el impacto de cada variable de control en su respectiva salida por ejemplo, cuánto impacto tiene v1 en T1, etc. La sintaxis de Mathematica es N [G*Transpose [Inverse [G]]]. La normalización RGA es esencial ya que a veces, no en este caso sin embargo, los valores de la matriz de ganancia pueden representar que una válvula tiene gran influencia en múltiples variables (es decir, una columna puede contener el valor más alto de múltiples filas). Para distinguir separaciones únicas entre estas influencias, se utiliza el RGA para normalizar la matriz de ganancia como se ve a continuación. Esto nos permite determinar las diferentes magnitudes de influencia que tiene la válvula en una salida para encontrar el efecto predominante en una salida. El RGA ilustra estas diferencias marginales en el impacto de las válvulas en las salidas variables, y nos permite hacer los mejores emparejamientos posibles.

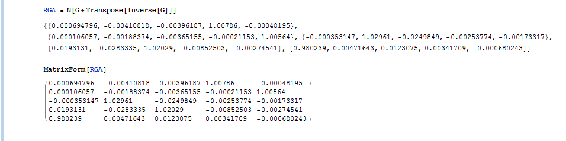
El mejor emparejamiento se descubre tomando el valor máximo de Matriz RGA para cada fila.

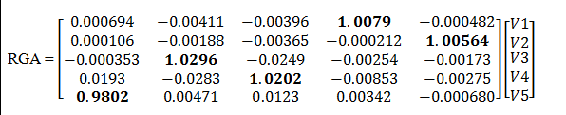
Los valores en negrita corresponden a la válvula que es el mejor emparejamiento para la salida individual. Al observar los valores en negrita, V1->P2 V2->T3, V3-> P1, V4-> T1, V5-> T2.

Ejercicio$\PageIndex{1}$

Para un sistema de control MIMO que contiene 4 variables diferentes manipuladas y 4 variables controladas diferentes, ¿cuántas configuraciones de control son posibles para el sistema?

a. 24
b. 4
c. 64
d. 256

Responder

Explicación: Matemáticamente, para un n x n manipulado por sistema variable controlado, el número de configuraciones de control posibles será n! o n factorial. Para un sistema variable 4x4, 4x3x2x1 = 24. Físicamente, el número de configuraciones de control se traduce en el número de posibles emparejamientos de entrada y salida.

Ejercicio$\PageIndex{2}$

En un caso de un sistema de matriz 2x2, si un elemento RGA en la primera fila calcula ser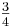 $textstyle\ frac {3} {4}$ . Según las propiedades RGA, ¿cuál es el otro elemento en esa misma fila?

a.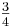 $textstyle\ frac {3} {4}$
b.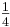 $textstyle\ frac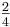 {1} {4}$
c. $textstyle\ frac {2} {4}$
d. No se puede determinar con la información dada.

Responder

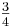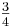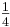
Explicación: Como se explicó anteriormente, todos los elementos de la RGA a través de cualquier fila, o hacia abajo cualquier columna deben sumar hasta la unidad (una). Para una matriz 2x2, si un elemento en una fila es $textstyle\ frac {3} {4}$ , el otro elemento debe ser 1- $textstyle\ frac {3} {4}$ = $textstyle\ frac {1} {4}$

Ejercicio$\PageIndex{3}$

RGA es útil para los ingenieros de procesos porque nos permite determinar:

a. Qué tamaño de matriz usar.
b. Qué valores propios y vectores propios están emparejados.
c. Qué pares de entrada y salida usar.
d. Cuando se prefiere el control de avance sobre el control de retroalimentación.

Responder

Explicación: Usando RGA, un ingeniero de procesos evaluará la ganancia relativa de emparejar cada entrada con cada salida para minimizar las interacciones no deseadas y maximizar las interacciones deseadas entre variables controladas y manipuladas en un sistema. Consulte la sección “Interpretación de la RGA” si está confundido sobre cómo se logra este análisis.

Referencias

Bereber, Ridvan. Métodos de Control de Procesos Basados en Modelos, Editores Académicos de Kluwer, 1994.
Lee, P.L., Newell, R.B., Cameron, I.T. Control y Gestión de Procesos, Blackie Académico y Profesional.
Romagnoli, José A., Palazoglu, Ahmet. Introducción al Control de Procesos, Taylor y Francis Group.
Shinskey, F.G. Sistemas de Control de Procesos: Aplicación, Diseño y Afinación, Cuarta Edición, McGraw-Hill, Inc., 1996.
Svrcek, W.Y., Mahoney, D.P., y Young, B.R. Un enfoque en tiempo real para el control de procesos, John Wiley and Sons, Ltd.
Universidad de Edimburgo, Ejercicio: Matrices de Ganancia Relativa, 2006
Universidad de Edimburgo, Sistemas Multivariables, 2007

Search

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)