13.9: Distribuciones Discretas - Hipergeométricas, Binomiales y Poisson

¿Qué son las distribuciones discretas?

Para explicar el significado y utilidad de las distribuciones dicretadas, es necesario introducir primero el tema de Variables Aleatorias. El término aleatorio en Variable Aleatoria se refiere a la idea de que cada resultado individual tiene las mismas posibilidades de ocurrir. Por lo tanto, cada resultado se determina aleatoriamente. Por ejemplo, una moneda justa tiene la misma probabilidad de voltear las cabezas que voltear las colas. De ahí que la variable aleatoria esté determinada por el resultado de voltear una moneda. Sin embargo, con frecuencia ocurre en la ingeniería química que cuando se realiza un proceso solo nos interesa alguna función del resultado en lugar del resultado en lugar del resultado en sí. Por ejemplo, en un reactor químico podríamos querer conocer la probabilidad de que dos moléculas colisionen y reaccionen para formar un producto a cierta temperatura, sin embargo es más útil conocer la suma de estas colisiones que forman producto en lugar de las incidencias individuales. Esto es analgoso para rodar dos dados y querer saber la suma de los dados en lugar de los números individuales tirados. Estos valores discretos definidos en algún espacio muestral componen lo que se llama Variables Aleatorias.

Ejemplo de Variable Aleatoria

Supongamos que nuestro experimento consiste en lanzar 4 monedas justas. Si definimos una variable X y la dejamos denotar el número de cabezas volteadas, entonces X es una variable aleatoria con posibles valores discretos de 0,1,2,3,4 con probabilidades respectivas:

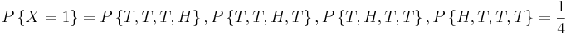
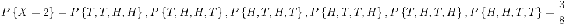
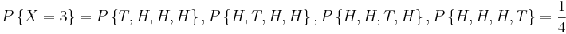
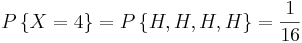
Podemos hacer lo mismo para la probabilidad de rodar sumas de dos dados. Si dejamos que Y denote la suma, entonces es una variable aleatoria que toma los valores de 2, 3, 4, 5, 6, 7, 8, 9, 10, & 12. En lugar de escribir las declaraciones de probabilidad podemos representar Y gráficamente:

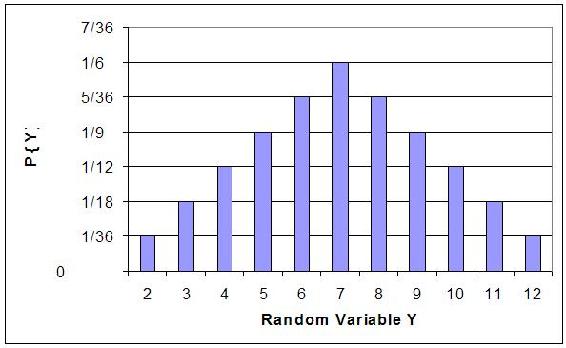
La gráfica traza la probabilidad de la Y para cada posible valor aleatorio en el espacio muestral (eje y) versus el valor aleatorio en el espacio muestral (eje x). De la gráfica se puede inferir que la suma con mayor probabilidad es Y = 7.

Estas son solo dos formas en las que se puede describir una variable aleatoria. A lo que esto lleva es representar estas variables aleatorias como funciones de probabilidades. Estas se llaman las distribuciones discretas o funciones de masa de probabilidad. Además, los eventos aleatorios independientes con probabilidades conocidas pueden ser agrupados en una variable aleatoria discreta. La Variable Aleatoria se define por ciertos criterios, como voltear la cabeza un cierto número de veces usando una moneda justa. La probabilidad de que una determinada variable aleatoria sea igual a un valor discreto se puede describir entonces mediante una distribución discreta. Por lo tanto, una distribución discreta es útil para determinar la probabilidad de un valor de resultado sin tener que realizar los ensayos reales. Por ejemplo, si quisiéramos saber la probabilidad de rodar un seis 100 veces de 1000 rollos, se puede usar una distribución en lugar de rodar realmente los dados 1000 veces.

Nota: Aquí hay una buena manera de pensar en la diferencia entre valores o distribuciones discretas y continuas. Si hay dos valores continuos en un conjunto, entonces existe un número infinito de otros valores continuos entre ellos. Sin embargo, los valores discretos solo pueden tomar valores específicos en lugar de divisiones infinitas entre ellos. Por ejemplo, una válvula que solo puede estar completamente abierta o completamente cerrada es análoga a una distribución discreta, mientras que una válvula que puede cambiar el grado de apertura es análoga a una distribución continua.

Las tres distribuciones discretas que discutimos en este artículo son la distribución binomial, la distribución hipergeométrica y la distribución de poisson.

Distribución binomial

Este tipo de distribución discreta se usa solo cuando se cumplen las dos condiciones siguientes:

1. La prueba solo tiene dos resultados posibles
2. La muestra debe ser aleatoria

Si se cumplen las dos condiciones anteriores, entonces uno es capaz de usar esta función de distribución para predecir la probabilidad de un resultado deseado. Las aplicaciones comunes de esta distribución van desde aplicaciones científicas y de ingeniería hasta aplicaciones militares y médicas. Por ejemplo, se puede usar una distribución binomial para determinar si un nuevo fármaco que se está probando ha contribuido o no (etiquetas “sí” o “no”) a aliviar los síntomas de una enfermedad.

Dado que solo son posibles dos resultados, se pueden denotar como M _S y M _F para el número de éxitos y número de fracasos respectivamente. El término p es la frecuencia con la que ocurrirá el número deseado, M _S o M _F. La probabilidad de una colección de los dos resultados está determinada por la siguiente ecuación.

\[P\left(M_{S}, M_{F}\right)=k p^{M_{S}}(1-p)^{M_{F}} \label{1} \]

k en la ecuación anterior es simplemente una constante de proporcionalidad. Para la distribución binomial se puede definir como el número de diferentes combinaciones posibles

\[k=C\left(\frac{M_{S}+M_{F}}{M_{S}}\right)=\frac{\left(M_{S}+M_{F}\right) !}{M_{S} ! M_{F} !} \label{2} \]

! es el operador factorial. Por ejemplo, ¡4! = 4 * 3 * 2 * 1 y x! = x * (x − 1) * (x − 2) *... * 2 * 1. En la ecuación anterior, ¡el término (M _S + M _F)! representa el número de formas en las que se podría organizar el número total de términos M _S y M _F y el denominador, ¡N _S! M _F! , representa el número de formas en que se podrían organizar los resultados que contienen M _S éxitos y fracasos de M _F. Por lo tanto, la probabilidad total de una colección de los dos resultados se puede describir combinando las dos ecuaciones anteriores para producir la función de distribución binomial.

\[P\left(M_{S}, M_{F}\right)=\frac{\left(M_{S}+M_{F}\right) !}{M_{S} ! M_{F} !} p^{M_{S}}(1-p)^{M_{F}} \label{3} \]

Esto se puede simplificar como la ecuación

\[\Gamma\{X-k\}-\frac{n !}{(n-k) ! k !} p^{k}(1-p)^{n} \label{4} \]

para\(k= k=-0,1,2,3 \dots\).

En la ecuación anterior, n representa el número total de posibilidades, o M _S + M _F, y k representa el número de resultados deseados, o M _S. Estas ecuaciones son válidas para todos los enteros no negativos de M _S, M _F, n y k y también para valores p entre 0 y 1.

A continuación se muestra una distribución binomial de muestra para 30 muestras aleatorias con una frecuencia de ocurrencia de 0.5 para cualquiera de los resultados. Este ejemplo es sinónimo de voltear una moneda 30 veces siendo k igual al número de volteretas que resultan en cabezas.

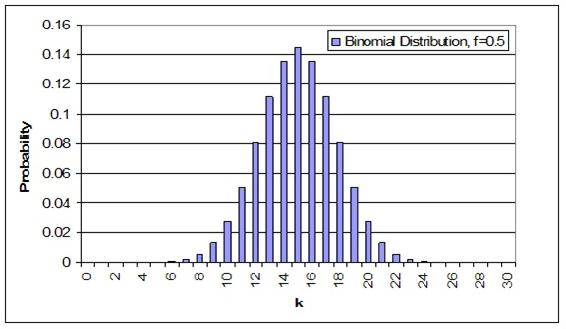
Una nota importante sobre estas distribuciones es que el área bajo la curva, o la probabilidad de que cada entero se sume, siempre suma hasta 1.

Se puede determinar la media y desviación estándar, la cual se describe en el artículo de Estadísticas Básicas, como se muestra a continuación.




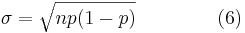
Un ejemplo de una pregunta común que puede surgir cuando se trata de distribuciones binomiales es “¿Cuál es la probabilidad de que ocurra un determinado resultado 33 — 66% de las veces?” En el caso anterior, sería sinónimo de la probabilidad de que las cabezas se levanten entre 10 y 20 de los juicios. Esto se puede determinar sumando las probabilidades individuales de cada entero de 10 a 20.

X > 33%) =\ suma_ {valores posibles} P (N_S) =P (10) +P (11) +... +P (19) +P (20)” src=”/@api /deki/files/19527/image-813.png “>


La probabilidad de que las cabezas resulten en 33 — 66% de las pruebas cuando una moneda es volteada 30 veces es 95.72%.

La probabilidad de distribución binomial también se puede calcular usando Mathematica. Esto simplificará los cálculos, ahorrará tiempo y reducirá los errores asociados al cálculo de la probabilidad utilizando otros métodos como una calculadora. La sintaxis necesaria para calcular la probabilidad en Mathematica se muestra a continuación en la captura de pantalla. También se da un ejemplo para diversas probabilidades basadas en 10 tiradas de monedas.

donde k es el número de eventos, n es el número de muestras independientes y p es la probabilidad conocida. El ejemplo anterior también genera un conjunto de valores para las probabilidades de obtener exactamente de 0 a 10 cabezas de 10 lanzamientos totales. Esto será útil porque simplifica el cálculo de probabilidades como obtener 0-6 cabezas, 0-7 cabezas, etc. de 10 tiradas porque las probabilidades solo necesitan ser sumadas de acuerdo a las probabilidades exactas generadas por la tabla.

Además de llamar a la función binomial generada anteriormente, Mathematica también tiene una función de distribución binomial incorporada que se muestra a continuación:

PDF [BinomialDistribution [n, p], k] donde n, p y k siguen representando las mismas variables que antes

Esta función incorporada se puede aplicar al mismo ejemplo de lanzamiento de monedas.

Como era de esperar, las probabilidades calculadas usando la función binomial incorporada coincide con las probabilidades derivadas de antes. Ambos métodos pueden ser utilizados para asegurar la precisión de los resultados.

Distribución de Poisson

Nota: Las variables utilizadas en esta sección se definen de la misma manera que se ha visto anteriormente en la sección “Distribución binomial”.

Una distribución de Poisson tiene varias aplicaciones, y es esencialmente un caso limitante derivado de la distribución binomial. Es más aplicable a una situación en la que se conoce el número total de éxitos, pero no lo es el número de ensayos. Un ejemplo de tal situación sería si conoces el número medio esperado de células cancerosas presentes por muestra y quieres determinar la probabilidad de encontrar 1.5 veces esa cantidad de células en una muestra dada, usarías una distribución de Poisson.

Para derivar la distribución de Poisson, primero debe comenzar con la función de distribución binomial.

\[P\{X-k\} = \frac{n!}{(n-k)! k!} p^{k}(1-p)^n \label{4A} \]

para\(k= 1,2,3 \ldots\).

Debido a que la distribución de Poisson no requiere una declaración explícita del número total de ensayos, se debe eliminar n de la función de distribución binomial. Esto se hace introduciendo primero una nueva variable (\(μ\)), que se define como el número esperado de éxitos durante el intervalo dado y puede describirse matemáticamente como:

\[\mu=n p \label{5} \]

Entonces podemos resolver esta ecuación para\(p\), sustituirla en Ecuación\ ref {5}, y obtener la Ecuación\ ref {7}, que es una versión modificada de la función de distribución binomial.

\[P\{X=k\}=\frac{n !}{(n-k) ! k !}\left(\frac{\mu}{n}\right)^{k}\left(1-\frac{\mu}{n}\right)^{n-k} \label{7} \]

Si mantenemos μ finito y permitimos que el tamaño de la muestra se acerque al infinito obtenemos la Ecuación\ ref {8}, que es igual a la función de distribución de Poisson. (Aviso para resolver la distribución de Poisson, no es necesario conocer el número total de ensayos)

\[P\{X=k\}=\frac{\mu^{k} e^{-\mu}}{k !} \label{8} \]

En la ecuación anterior:

• e es la base del logaritmo natural (e = 2.71828...)
• k es el número de ocurrencias de un evento
• k! es el factorial de k
• μ es un número real positivo, igual al número esperado de ocurrencias que ocurren durante el intervalo dado.

Usando la distribución de Poisson, se puede hacer una gráfica de probabilidad versus número de éxitos para varios números diferentes de éxitos.

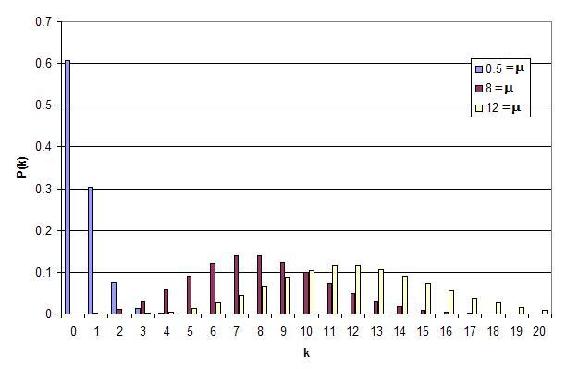
Esta gráfica representa varias características clave de un proceso de Poisson.

1. El número de éxitos es independiente del tiempo transcurrido desde el último evento.
2. Las probabilidades, o los resultados, son discretos.
3. La probabilidad de dos o más éxitos en un intervalo corto es extremadamente pequeña (aproximadamente cero).

Estas reglas insinúan que los procesos de Poisson solo modelan eventos raros, pero esto no es cierto. Lo que dicen estas características es que si estás limitado a una pequeña ventana de intervalo, observarás menos de dos eventos. Es importante saber que la distribución de Poisson es en realidad una aproximación de la distribución binomial. A medida que n aumenta y p disminuye, la distribución de Poisson se vuelve igual a la distribución binomial.

Distribución Hipergeométrica

Nota: Las definiciones de las variables en esta sección son diferentes a las secciones anteriores.

Una función de distribución hipergeométrica se usa solo si se pueden cumplir las siguientes tres condiciones:

1. Solo dos resultados son posibles
2. La muestra debe ser aleatoria
3. Las selecciones no se reemplazan

Las distribuciones hipergeométricas se utilizan para describir muestras donde las selecciones de un conjunto binario de elementos no son reemplazadas. Esta distribución se aplica en situaciones con un número discreto de elementos en un grupo de N elementos donde hay K elementos que son diferentes. Como ejemplo sencillo imagina que estamos quitando 10 bolas de un frasco de bolas mixtas rojas y verdes sin reemplazarlo. ¿Cuál es la posibilidad de seleccionar 2 bolas verdes? ¿5 bolas rojas? En términos generales, si hay K bolas verdes y N bolas totales, la posibilidad de seleccionar k bolas verdes seleccionando n bolas viene dada por

\[P(x=k)=\frac{(\# \text { of ways to select } k \text { green balls })(\# \text { of ways to select } n-k \text { red balls })}{(\text { total number of ways to select) }} \label{9} \]

Como otro ejemplo, digamos que hay dos reactivos sentados en un CSTR que suman a N moléculas. El tercer reactivo puede reaccionar con A o B para hacer uno de dos productos. Digamos ahora que hay K moléculas del reactivo A, y N-K moléculas del reactivo B. Si dejamos que n denote el número de moléculas consumidas, entonces la probabilidad de que se consumieron k moléculas de reactivo de A puede ser descrita por la distribución hipergeométrica. Nota: Esto supone que no hay reacciones inversas o secundarias con los productos.

En términos matemáticos esto se convierte

\[P\{X=k\}=\frac{(N-K) ! K ! n !(N-n) !}{k !(K-k) !(N-K+k-n) !(n-k) ! N !} label{10} \nonumber \]

donde,

• N = número total de artículos
• K = número total de elementos con rasgo deseado
• n = número de ítems en la muestra
• k = número de ítems con rasgo deseado en la muestra

Esto se puede escribir en taquigrafía como

\ [P\ {x=k\} =\ frac {\ izquierda (\ begin {array} {l}
K\
k
\ end {array}\ right)\ left (\ begin {array} {l}
N-K\
n-k
\ end {array}\ right)} {\ left (\ begin {array} {l}
N\
n
\ end {array}\ right)}\ label {11} \]

donde

\ [\ left (\ begin {array} {l}
A\\
B
\ end {array}\ right) =\ frac {A!} {(A-B)! B!} \ label {12}\]

La fórmula se puede simplificar de la siguiente manera: Hay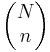 posibles muestras (sin reemplazo). Hay 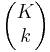formas de obtener k bolas verdes y hay 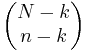formas de llenar el resto de la muestra con bolas rojas.

Si se trazan las probabilidades P frente a k, entonces se ve una gráfica de distribución similar a los otros tipos de distribuciones.

Ejemplo\(\PageIndex{1}\)

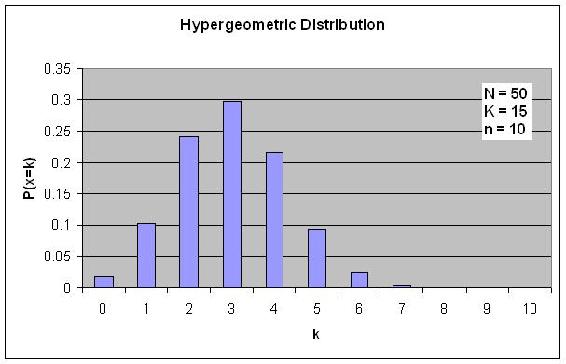
Supongamos que tienes una bolsa llena de 50 canicas, 15 de las cuales son de color verde. ¿Cuál es la probabilidad de elegir exactamente 3 canicas verdes si se seleccionan un total de 10 canicas?

Solución

\ [P\ {X=3\} =\ frac {\ izquierda (\ begin {array} {c} 15\\ 3
\ end {array}\ derecha)\ left (\ begin {array} {c}
50-15\\
10-3
\ end {array}\ right)} {\ left (\ begin {array} {c}
50\
10
\ end {array}\ right)}]

\[P\{X=3\}=\frac{(50-15) ! 15 ! 10 !(50-10) !}{3 !(15-3) !(50-15+3-10) !(10-3) ! 50 !} \nonumber \]

\[P\{X=3\}=0.2979 \nonumber \]

Fisher's exacto

Un caso especial de la distribución hipergeométrica es el método exacto de Fisher. La exacta de Fisher es la probabilidad de muestrear una configuración específica de una tabla de 2 por 2 con marginales restringidos. Los marginales en este caso se refieren a las sumas para cada fila y cada columna. Por lo tanto, cada exacto de Fisher tendrá 4 marginales, siendo esos 4 la suma de la primera columna, la suma de la segunda columna, la suma de la primera fila y la suma de la segunda fila. Dado que estos valores son constantes, eso también significa que la suma de todos los elementos de la tabla siempre será igual a lo mismo. Esto se aclara con la imagen de abajo:

En la imagen de arriba, marginales constantes significarían que E, F, G y H se mantendrían constantes. Dado que esos valores serían constantes, yo también sería constante ya que se me puede pensar como la suma de E y F o G y H son de los cuales son constantes.

En teoría esta prueba puede ser utilizada para cualquier tabla de 2 por 2, pero más comúnmente, se usa cuando se violan las condiciones de tamaño de muestra necesarias para usar la prueba z o la prueba de chi-cuadrado. La siguiente tabla muestra tal situación:

A partir de este p _pescador se puede calcular:

\[p_{\text {fisher }}=\frac{(a+b) !(c+d) !(a+c) !(b+d) !}{(a+b+c+d) ! a ! b ! c ! d !} \nonumber \]

donde el numerador es el número de formas en que se pueden organizar los marginales, el primer término en el denominador es el número de formas en que se puede ordenar el total, y los términos restantes en el denominador son el número de formas en que se puede organizar cada observación.

Como se indicó anteriormente, este valor calculado es sólo la probabilidad de crear el 2x2 específico a partir del cual se calculó el valor p _fisher.

Otra forma de calcular p _fisher es usar Mathematica. La sintaxis así como un ejemplo con números se pueden encontrar en la captura de pantalla a continuación del cuaderno de Mathematica. Para mayor aclaración, la captura de pantalla a continuación también muestra el valor calculado de p _fisher con números. Esto es útil de saber porque reduce las posibilidades de hacer un simple error de álgebra.

Otra herramienta útil para calcular p _fisher es el uso de herramientas disponibles en línea. El siguiente enlace proporciona una calculadora en línea útil para calcular rápidamente p _fisher. [1]

El uso de Mathematica o una herramienta de cálculo similar simplificará enormemente el proceso de resolución para p _fisher.

Después de encontrar el valor de p _fisher, el valor p es la suma de los valores exactos de Fisher para el caso o casos más extremos, si corresponde. El valor p determina si la hipótesis nula es verdadera o falsa. Un ejemplo de esto se puede encontrar en el ejemplo de distribución hipergeométrica elaborado a continuación.

Encontrar el valor p

Como se detalla aquí: [2], el valor p permite rechazar la hipótesis nula o no rechazar la hipótesis nula. El hecho de que la hipótesis nula no sea rechazada no significa que se defienda, solo significa que actualmente no hay evidencia suficiente para rechazar la hipótesis nula.

Para multar el valor p, es necesario encontrar las probabilidades no sólo de una tabla específica de resultados, sino de resultados considerados aún más “extremos” y luego sumar esas probabilidades calculadas. Un ejemplo de esto se muestra a continuación en el ejemplo 2.

Lo que se considera “más extremo” depende de la situación. En el sentido más general, más extremo significa más lejos del resultado esperado o aleatorio.

Una vez que se hayan creado las tablas más extremas y se haya obtenido la probabilidad de cada valor, se pueden sumar juntas para encontrar el valor p correspondiente a la tabla menos extrema.

Es importante señalar que si se sumaran las probabilidades para cada tabla posible, el resultado sería invariablemente uno. Esto debe esperarse ya que la probabilidad de que una tabla se incluya en toda la población de tablas es de 1.

Ejemplo\(\PageIndex{1}\)

La tabla de ejemplo a continuación correlaciona la cantidad de tiempo que uno pasó estudiando para un examen con lo bien que le fue en un examen.

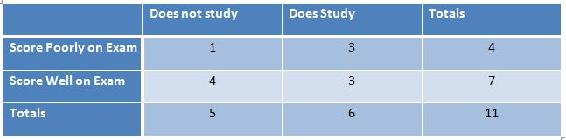
Hay 5 configuraciones posibles para la tabla anterior, que se enumera en el código de Mathematica a continuación. Todo el p _fisher para cada configuración se muestra en el código de Mathematica a continuación.

Ejemplo\(\PageIndex{1}\)

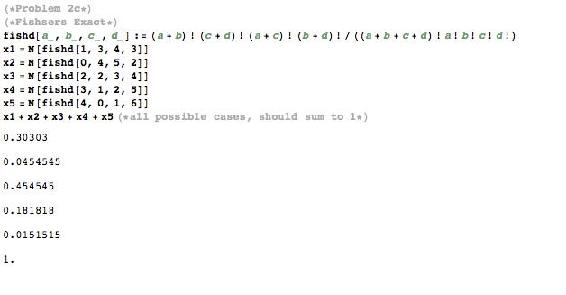
¿Cuáles son las probabilidades de elegir las muestras descritas en la tabla siguiente con estos marginales en esta configuración o una más extrema?

Solución

Primero calcule la probabilidad para la configuración inicial.

\[p_{\text {fisher }}=\frac{6 ! 19 ! 6 ! 19 !}{25 ! 5 ! 1 ! 1 ! 18 !}=0.000643704 \nonumber \]

Luego crea una nueva tabla que muestre el caso más extremo que también mantenga los mismos marginales que estaban en la tabla original.

Después calcula la probabilidad para el caso más extremo.

\[p_{\text {fisher }}=\frac{6 ! 19 ! 6 ! 19 !}{25 ! 6 ! 0 ! 0 ! 19 !}=0.00000564653 \nonumber \]

Finalmente sumar las dos probabilidades juntas.

\[p_{fisher} = 0.000643704 + 0.00000564653 = 0.00064 \nonumber \]

Función máxima de entropía

El principio de máxima entropía utiliza toda la información comprobable sobre múltiples distribuciones de probabilidad dadas para describir la distribución de probabilidad verdadera maximizando la entropía de información. Para derivar una distribución con el principio de máxima entropía, se obtiene alguna información comprobable I sobre alguna cantidad x. Esta información se expresa como m restricciones sobre los valores de expectativa de las funciones f _k. Esto hace que la distribución de probabilidad bayesiana satisfaga:

\[F_{k}=\sum_{i=1}^{n} \operatorname{Pr}\left(x_{i} \mid I\right) f_{k}\left(x_{i}\right) \nonumber \]

con\(k=1, \cdots, m\).

También sabemos que todas estas probabilidades deben sumar a 1, por lo que se introduce la siguiente restricción:

\[\sum_{i=1}^{n} \operatorname{Pr}\left(x_{i} \mid I\right)=1 \nonumber \]

Entonces la distribución de probabilidad con máxima entropía de información que satisface todas estas restricciones es:

\[\operatorname{Pr}\left(x_{i} \mid I\right)=\frac{1}{Z\left(\lambda_{1}, \cdots, \lambda_{m}\right)} \exp \left[\lambda_{1} f_{1}\left(x_{i}\right)+\cdots+\lambda_{m} f_{m}\left(x_{i}\right)\right] \nonumber \]

La constante de normalización está determinada por la función de partición clásica:

\[Z\left(\lambda_{1}, \cdots, \lambda_{m}\right)=\sum_{i=1}^{n} \exp \left[\lambda_{1} f_{1}\left(x_{i}\right)+\cdots+\lambda_{m} f_{m}\left(x_{i}\right)\right] \nonumber \]

Los parámetros λ _k son multiplicadores Lagrange con valores determinados por:

\[F_{k}=\frac{\partial}{\partial \lambda_{k}} \log Z\left(\lambda_{1}, \cdots, \lambda_{m}\right) \nonumber \]

Todas las distribuciones conocidas en estadística son distribuciones de entropía máxima dadas las restricciones de momento adecuadas. Por ejemplo, si asumimos que lo anterior estaba restringido por el segundo momento, y entonces se derivaría la distribución gaussiana con una media de 0 y una varianza del segundo momento.

El uso de la función de distribución máxima de entropía pronto se volverá más predominante. En 2007 se había demostrado que la Regla de Bayes y el Principio de Máxima Entropía eran compatibles. También se demostró que la máxima entropía reproduce todos los aspectos de los métodos de inferencia bayesianos ortodoxos. Esto permite a los ingenieros abordar problemas que no podían ser simplemente abordados por el principio de máxima entropía o métodos bayesianos, individualmente, en el pasado.

Resumen

Las tres distribuciones discretas que se discuten en este artículo incluyen las distribuciones Binomial, Hipergeométrica y Poisson. Estas distribuciones son útiles para encontrar las posibilidades de que una determinada variable aleatoria produzca un resultado deseado.

Función de distribución binomial

La función de distribución binomial se utiliza cuando solo hay dos resultados posibles, un éxito o un faliure. Un éxito ocurre con la probabilidad p y un fracaso con la probabilidad 1-p. Supongamos ahora que en n ensayos independientes la variable binomial aleatoria X representa el número de éxitos. La siguiente ecuación se aplica a las variables aleatorias binomiales:

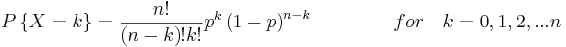
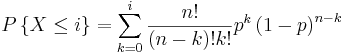
Función de distribución de Poisson

La distribución de Poisson se puede utilizar en una gran variedad de situaciones. También se puede utilizar para aproximar la Distribución Binomial cuando n es grande y p es pequeña produciendo un np moderado.

El siguiente ejemplo es una situación en la que se aplica la Distribución de Poisson: Supongamos que un CSTR está lleno de moléculas y la probabilidad de que una molécula reaccione para formar el producto es pequeña (digamos debido a una baja temperatura) mientras que el número de moléculas es grande, entonces la función de distribución de probabilidad encajaría el pozo de Distribución de Poisson (Nota: todas las moléculas son iguales aquí, a diferencia del ejemplo hipergeométrico a seguir). Otros ejemplos incluyen, el número de números telefónicos incorrectos que se marcan cada día o el número de personas en una comunidad que viven hasta los 100 años de edad. La siguiente ecuación es la función Distribución de Poisson:

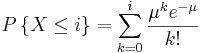
Resumen de Key Distributions

Resumen de Aproximaciones de Distribución

Hay muchas aproximaciones útiles para variables aleatorias discretas. Una aproximación importante es aquella que produce una distribución normal porque permite que los intervalos de confianza y probabilidades sean continuos. Adicionalmente, dado que la distribución normal es tan bien entendida, se usa por conveniencia cuando se habla con quienes aún no han estudiado la teoría de la probabilidad. A continuación se muestra una tabla de aproximaciones útiles. La mayor parte de la teoría detrás de estas aproximaciones se encuentra en la aplicación del Teorema de Límite Central y la Ley de Grandes Números pero éstas están fuera del alcance de este texto.

El gráfico anterior se puede leer como “Una variable aleatoria bajo la siguiente distribución puede ser aproximadamente una <blank>variable aleatoria cuando se cumplen los siguientes requisitos”. Por ejemplo, se puede leer la línea final de la tabla: “Una variable aleatoria que sigue a una distribución de Poisson con el parámetro λ es aproximadamente una variable aleatoria Normal continua donde la media es λ y la varianza es λ asumiendo que hay al menos 100 muestras que se han tomado”.

Ejemplo\(\PageIndex{1}\)

Para que una vacunación contra la poliomielitis sea eficiente, la inyección debe contener al menos 67% de la molécula apropiada, VPOLIO. Para garantizar la eficacia, una gran compañía farmacéutica fabricó un lote de vacunas con cada jeringa que contenía 75% de VPOLIO. Su médico extrae una jeringa de este lote que debe contener 75% de VPOLIO. ¿Cuál es la probabilidad de que tu tiro, te impida con éxito adquirir Polio? Supongamos que la jeringa contiene 100 moléculas y que todas las moléculas son capaces de ser entregadas desde la jeringa a su torrente sanguíneo.

Solución

Esto se puede hacer configurando primero la función de distribución binomial. Para ello, lo mejor es configurar una hoja de cálculo de Excel con valores de k de 0 a 100, incluyendo cada entero. La frecuencia de extracción de una molécula VPOLIO es de 0.75. Dibujando aleatoriamente cualquier molécula, la probabilidad de que esta molécula nunca sea VPOLIO, o en otras palabras, la probabilidad de que tu disparo contenga 0 moléculas de VPOLIO es

\[P=\frac{100 !}{(100-0 !) ! 0 !}(0.75)^{0}(1-0.75)^{100-0} \nonumber \]

Tenga en cuenta que 0! =1

Tu hoja de cálculo debe contener probabilidades para todos los valores posibles de VPOLIO en la toma. Un enlace a nuestra hoja de cálculo se puede ver al final de este artículo. A continuación se muestra una gráfica de nuestra distribución.

El siguiente paso es sumar las probabilidades de 67 a 100 de las moléculas siendo VPOLIO. Este es el cálculo se muestra en la hoja de cálculo de muestra. La probabilidad total de que al menos 67 de las moléculas sean VPOLIO es de 0.9724. Por lo tanto, hay un 97.24% de probabilidad de que estés protegido de la Polio.

Ejemplo\(\PageIndex{1}\): Gaussian Approximation Of A Binomial Distribution

El cálculo de la función binomial con n mayor a 20 puede ser tedioso, mientras que el cálculo de la función Gauss siempre es simple. Para ilustrar esto, considere el siguiente ejemplo.

Supongamos que queremos saber la probabilidad de conseguir 23 cabezas en 36 tiradas de una moneda. Esta probabilidad viene dada por la siguiente distribución binomial:

\[P=\frac{36 !}{23 ! 13 !}(0.5)^{36}=3.36 \% \nonumber \]

Para utilizar una Aproximación Gaussiana, primero debemos calcular la media y la desviación estándar.




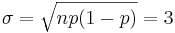
Ahora podemos aproximar la probabilidad por la función Gauss a continuación.

\[P=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-X)^{2}}{2 \sigma^{2}}}=3.32 \% \nonumber \]

Esta aproximación es muy cercana y requiere mucho menos cálculo debido a la falta de factoriales. La utilidad de la aproximación gaussiana es aún más evidente cuando n es muy grande y las factoriales implican un cálculo muy intensivo.

Ejemplo\(\PageIndex{1}\): Worked out Hypergeometric Distribution

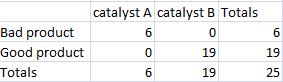
Una maestra tiene 12 alumnos en su clase. En su examen más reciente, 7 estudiantes reprobaron mientras que los otros 5 estudiantes aprobaron. Curiosa de por qué tantos alumnos reprobaron el examen, ella realizó una encuesta, preguntando a los alumnos si estudiaron o no la noche anterior. De los estudiantes que fallaron, 4 estudiantes sí estudiaron y 3 no. De los alumnos que pasaron, 1 estudiante sí estudió y 4 no. Después de ver los resultados de esta encuesta, la maestra concluye que quienes estudian casi siempre fracasarán, y ella procede a hacer cumplir una política de “no estudiar”. ¿Fue esta la conclusión y acción correctas?

Solución

Esta es una situación perfecta para aplicar la prueba exacta de Fisher para determinar si existe alguna asociación entre estudiar y rendimiento en el examen. Primero, cree una tabla de 2 por 2 que describa este resultado particular para la clase, y luego calcule la probabilidad de ver esta configuración exacta. Esto se muestra a continuación.

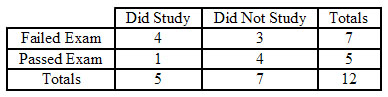
\[p_{\text {fisher }, 1}=\frac{(4+3) !(1+4) !(4+1) !(3+4) !}{(4+3+1+4) ! 4 ! 3 ! 1 ! 4 !}=0.221 \nonumber \]

A continuación, cree tablas de 2 por 2 que describan cualquier configuración con los mismos márgenes exactos que sean más extremos que la mostrada anteriormente, y luego calcule la probabilidad de ver cada configuración. Afortunadamente, para este ejemplo, sólo hay una configuración que es más extrema, que se muestra a continuación.

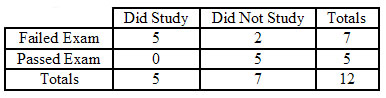
\[p_{\text {fisher }, 2}=\frac{(5+2) !(0+5) !(5+0) !(2+5) !}{(5+2+0+5) ! 5 ! 2 ! 0 ! 5 !}=0.0265 \nonumber \]

Finalmente, pruebe la significancia calculando el valor p para la declaración del problema. Esto se hace sumando todas las probabilidades previamente calculadas.

\[p=p_{\text {fisher }, 1}+p_{\text {fisher }, 2}=0.221+0.0265=0.248 \nonumber \]

Así, el valor p es mayor a 0.05, que es el nivel estándar aceptado de confianza. Por lo tanto, la hipótesis nula no puede ser rechazada, lo que significa que no existe una asociación significativa entre el estudio y el rendimiento en el examen. Desafortunadamente, el maestro se equivocó al hacer cumplir una política de “no estudiar”.

Ejemplo\(\PageIndex{1}\): Poisson

La hormona PREGO solo se encuentra en el cuerpo humano femenino durante el inicio del embarazo. Solo hay 1 molécula de hormona por cada 10,000 que se encuentra en la orina de una mujer embarazada. Si se nos da una muestra de 5,000 moléculas hormonales ¿cuál es la probabilidad de encontrar exactamente 1 PREGO? Si necesitamos al menos 10 moléculas de PREGO para ser 95% positivas de que una mujer está embarazada, ¿cuántas moléculas hormonales totales debemos recolectar? Si la concentración de moléculas hormonales en la orina es de 100,000 moléculas/ml de orina, ¿cuál es la cantidad mínima de orina (en mL) necesaria para asegurar una prueba precisa (95% positiva para el embarazo)?

Solución

Esto satisface las características de un proceso de Poisson porque

1. Las moléculas de hormona PREGO se distribuyen aleatoriamente en la orina
2. Los números de moléculas hormonales son discretos
3. Si el tamaño del intervalo se hace más pequeño (es decir, nuestro tamaño de muestra se reduce), la probabilidad de encontrar una molécula de hormona PREGO va a cero

Por lo tanto asumiremos que el número de moléculas de hormona PREGO se distribuye de acuerdo con una distribución de Poisson.

Para responder a la primera pregunta, comenzamos por encontrar el número esperado de moléculas de hormona PREGO:

\[\mu=n p \nonumber \]

\[\mu=(5,000)\left(\frac{1}{10,000}\right)=0.5 \nonumber \]

A continuación utilizamos la distribución de Poisson para calcular la probabilidad de encontrar exactamente una molécula de hormona PREGO:

\[P\{X=k\}=\frac{\mu^{k} e^{-\mu}}{k !}=0.303 \nonumber \]

dónde\(k=1\) y\(\mu=0.5\).

El segundo problema es más difícil porque estamos calculando n. Comenzamos como antes calculando el número esperado de moléculas de hormona PREGO:

\[\mu=n p=\frac{n}{10,000} \nonumber \]

Ahora aplicamos la ecuación de la función de distribución de Poisson:

\[F\{X \geq 10\}-0.95-\sum_{k=1}^{\infty} \frac{\mu^{k} e^{\mu}}{k !}-1.0-\sum_{k=0}^{-5} \frac{\mu^{k} e^{\mu}}{k !}-1.0-\sum_{k=1}^{10}\left(\left(\frac{n^{\prime}}{10.000}\right)^{k} \frac{\left.e^{-\left(\frac{u}{k, 00 !}\right.}\right)}{k !}\right) \nonumber \]

Es más fácil resolver esto en Mathematica:

La función FindRoot [] se utilizó en Mathematica porque la función Solve [] tiene problemas para resolver polinomios de orden de grado mayor a 4 así como funciones exponenciales. Sin embargo, FindRoot [] requiere una suposición inicial para la variable que intenta resolverse, en este caso n se estimó en alrededor de 100,000. Como puedes ver en la captura de pantalla de Mathematica el número total de moléculas hormonales necesarias para estar 95% seguro de embarazo (o 95% de probabilidad de tener al menos 10 moléculas PREGO) fue de 169,622 moléculas.

Para el último paso utilizamos la concentración de moléculas hormonales totales que se encuentran en la orina y calculamos el volumen de orina requerido para contener 169,622 moléculas hormonales totales ya que esto arrojará una probabilidad del 95% de una prueba precisa:

Ejemplo\(\PageIndex{1}\): Gaussian Approximation to a Poisson Distribution

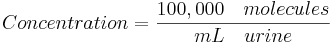
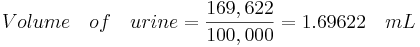
Para ilustrar la aproximación gaussiana a la distribución de Poisson, considere una distribución donde la media (\(μ\)) es 64 y el número de observaciones en un intervalo definido (\(N\)) es 72. Determinar la probabilidad de estas 72 observaciones?

Solución

Uso de la distribución de Poisson

\ [\ begin {alinear*}
P (N) &=e^ {-\ mu}\ cdot\ frac {\ mu^ {N}} {N!} \\ [4pt]
P (72) &=e^ {-64}\ cdot\ frac {64^ {7} 2} {72!} =2.9\%
\ end {align*}\ nonumber\]

Esto puede ser difícil de resolver cuando los parámetros\(N\) y\(μ\) son grandes. Una aproximación más fácil se puede hacer con la función gaussiana:

\[P(72)=G_{64,8}=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-X)^{2}}{2 \sigma^{2}}}=3.0 \% \nonumber \]

dónde,\(X=μ\) y\(σ= \sqrt{\mu}\).

Ejercicio\(\PageIndex{1}\)

Todas las siguientes son características de la distribución de Poisson EXCEPTO:

1. El número de éxitos es independiente del intervalo
2. Hay números imaginarios
3. Las probabilidades, o los resultados, son discretos
4. Dos o más éxitos en un intervalo corto es extremadamente pequeño

Responder

TBA

Ejercicio\(\PageIndex{1}\)

Si hay K bolas azules y N bolas totales, la posibilidad de seleccionar k bolas azules seleccionando n bolas en notación taquigráfica viene dada por:
a)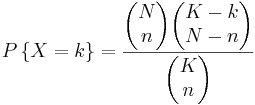
b)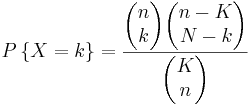
c)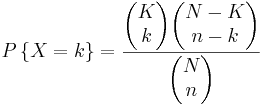
d)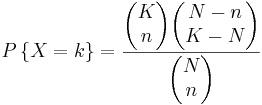

Responder

TBA

Presentación de Distribución Discreta: Clown Time

www.youtube.com/v/6WoiEU664ew

Referencias

• Ross, Sheldon: Un primer curso en probabilidad. Upper Saddle River: Prentice Hall, Capítulo 4.
• Uts, J. y R. Hekerd. Mente en Estadística. Capítulo 15 - Más Acerca de Inferencia para Variables Categóricas. Belmont, CA: Brooks/Cole - Thomson Learning, Inc. 2004.
• Weisstein, Eric W.: MathWorld - Distribuciones Discretas. Fecha de acceso: 20 noviembre 2006. MathWorld
• Woolf, Peter y Amy Keating, Christopher Burge, Michael Yaffe: Primer de Estadística y Probabilidad para Biólogos Computacionales. Boston: Instituto Tecnológico de Massachusetts, pp 3.1 - 3.21.
• Wikipedia-Principio de máxima entropía. Fecha de acceso: 10 diciembre 2008. [3]
• Giffin, A. y Caticha, A., 2007, [4].