13.11: Comparaciones de dos medias

Última actualización
Guardar como PDF

Page ID: 85477

Daniel Katzman, Jason Noelanders, Jessica Moreno, & Mark Winston-Galant
University of Michigan

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los ingenieros a menudo deben comparar conjuntos de datos para determinar si los resultados de sus análisis son estadísticamente equivalentes. Un sensor emite una serie de valores y el ingeniero debe determinar si el sensor es preciso y si los valores son precisos de acuerdo con un estándar. Para realizar esta evaluación se utilizan métodos estadísticos. Un método compara las distribuciones de probabilidad y otro utiliza la prueba t de Student en dos conjuntos de datos. Microsoft Excel también cuenta con funciones que realizan la prueba t que generan una probabilidad fraccionaria para evaluar la hipótesis nula (Basic Statistics).

Distribuciones

Distribuciones Generales

Las distribuciones se rigen por la función de densidad de probabilidad:

\[f(x)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}\right) \nonumber \]

donde

$\sigma$es la desviación estándar de un conjunto de datos
$\sigma$es la media del conjunto de datos
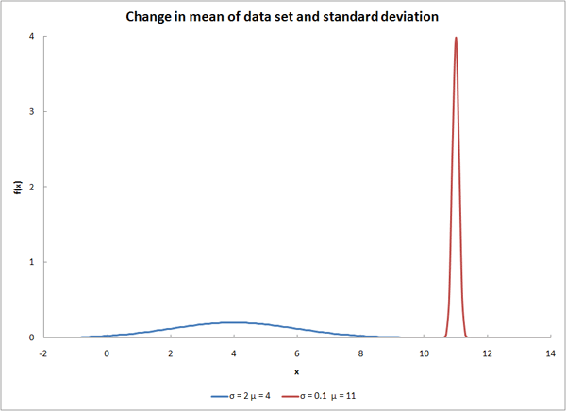
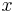$\,$ es el valor de entrada

Esta ecuación da una curva típica de campana. El cambio$\sigma$ alterará la forma de la curva, como se muestra en la gráfica a continuación.

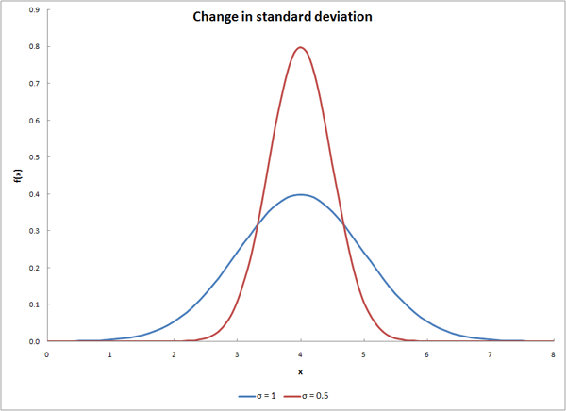
El cambio$\mu$ desplazará la curva a lo largo del eje x, como se muestra a continuación.

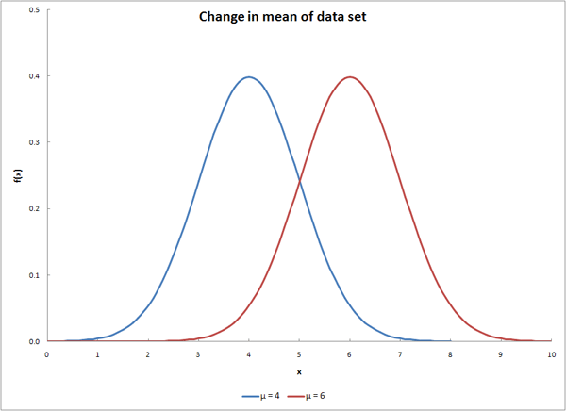
Cambiar ambas variables tendrá un resultado similar al gráfico de abajo.

Para una mirada más profunda a las distribuciones, vaya a (Distribuciones).

Distribuciones superpuestas

La superposición entre dos curvas de distribución ayuda a determinar la probabilidad de que los dos conjuntos de datos sean de la misma distribución. El valor de probabilidad aumenta a medida que aumenta la superposición. El solapamiento se muestra como la región púrpura en la gráfica a continuación.

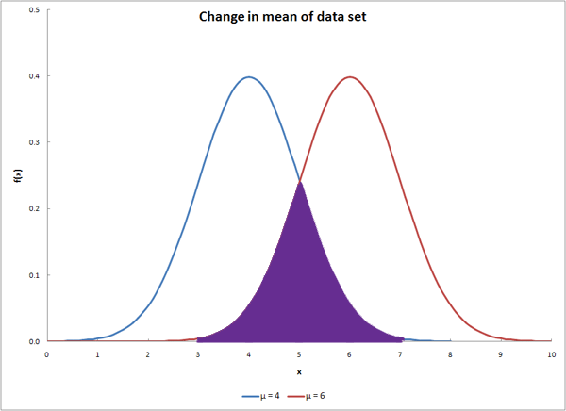
Comparación de dos medias

Probabilidad

La similitud de dos conjuntos de datos se puede determinar encontrando la probabilidad de superposición. Esto se ilustra mediante la siguiente ecuación:

\ [P (\ text {superposición}) =\ int_ {-\ infty} ^ {\ infty}\ min\ izquierda\ {\ begin {array} {l}
p_ {s}\ izquierda (k\ mid\ theta_ {s}\ derecha)\
p_ {o}\ izquierda (k\ mid\ theta_ {0}\ derecha)
\ end {array}\ derecha. \ nonumber\]

Las funciones contenidas dentro de la integral son las distribuciones de probabilidad de cada conjunto de datos respectivo. La ecuación suma la distribución de probabilidad menor de cada conjunto de datos. Después de usar esta ecuación, la solución será un valor con un rango entre 0 y 1 indicando la magnitud de la probabilidad de superposición. Un valor de 0 demuestra que los dos conjuntos de datos no se superponen en absoluto. Un valor de 1 demuestra que los dos conjuntos de datos se superponen completamente. Los valores entre 0 y 1 dan el grado de superposición entre los dos conjuntos de datos. Esta probabilidad no es la misma que el intervalo de confianza que se puede calcular con las pruebas t.

Prueba T de Estudiante

La prueba t de Student es extremadamente útil para comparar dos medias. Existen diversas versiones de la prueba t de estudiante, dependiendo del contexto del problema. Generalmente, la prueba cuantifica la relación señal/ruido, donde la señal es la diferencia de medias y el ruido es una función del error alrededor de las medias. Si la señal es grande y el ruido es pequeño, uno puede estar más seguro de que la diferencia entre las medias es “real” o significativa. Para probar una diferencia significativa, necesitamos desmentir la hipótesis nula. La “hipótesis nula” (Ho) es que no hay diferencia entre las dos medias. Si somos capaces de desmentir la “hipótesis nula” entonces podremos decir que los dos grupos son estadísticamente diferentes dentro de un nivel de confianza conocido.

Las extremidades en cualquiera de los extremos de una distribución de probabilidad se denominan las “colas” de la distribución. La evaluación de la significancia de un valor t calculado dependerá de si es necesario o no considerar ambas colas de la distribución. Esto dependerá de la forma de la hipótesis nula. Si tu hipótesis nula es una igualdad, entonces se debe considerar el caso en el que una media es mayor y menor; es decir, solo se debe tener en cuenta una cola de la distribución. Por el contrario, si la hipótesis nula es una desigualdad, entonces solo te preocupa el dominio de los valores para una media ya sea menor o mayor que la otra media; es decir, ambas colas de la distribución deben ser contabilizadas.

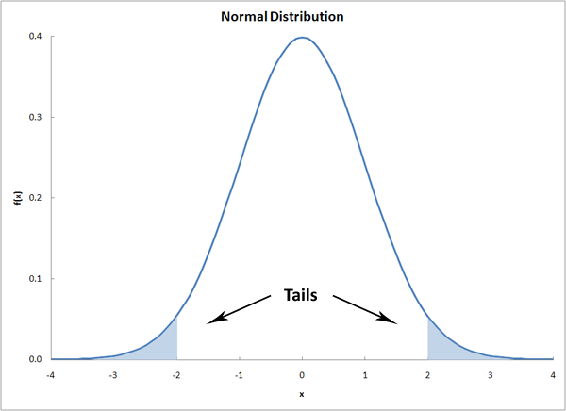
Más información: la distribución t del estudiante

La distribución t es la distribución de probabilidad resultante con una población de muestra pequeña. Esta distribución es la base de la prueba t, con el fin de encontrar la significancia estadística entre dos medias de datos. Esta distribución está en la forma de una función hiperbólica generalizada (Que entra en detalles que solo se desordenarían aquí. Para mayor información, el sitio de Wikipedia contiene mucha información sobre el tema: es.wikipedia.org/wiki/Generalised_Hyperbolic_distribution).

La distribución t se usa comúnmente cuando se desconoce la desviación estándar, o no se puede conocer (es decir: un conjunto poblacional muy pequeño). Cuando los conjuntos de datos son grandes, o se asume una desviación estándar, la distribución t no es muy útil para un análisis estadístico, y se deben utilizar otros métodos de análisis. Un ejemplo de la distribución t se puede ver a continuación:

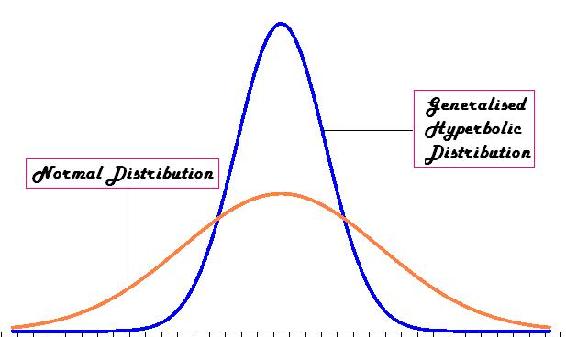
Comparación de dos medias verdaderas desconocidas cuando las desviaciones estándar de la muestra son aproximadamente iguales

El primer supuesto aceptado es que cuando se comparan dos medias de muestra, las desviaciones estándar son aproximadamente iguales. Este método requiere el promedio, la desviación estándar y el número de mediciones tomadas para cada conjunto de datos. Luego, las desviaciones se agrupan en una desviación estándar. La ecuación para esta prueba t es la siguiente:

\[t=\frac{\text { Signal }}{\text { Noise }}=\frac{\bar{x}_{1}-\bar{x}_{2}}{S_{\text {pooled }}} \sqrt{\frac{n_{1} n_{2}}{n_{1}+n_{2}}} \nonumber \]

donde:

\[S_{\text {pooled }}=\sqrt{\frac{s_{1}^{2}\left(n_{1}-1\right)+s_{2}^{2}\left(n_{2}-1\right)}{n_{1}+n_{2}-2}} \nonumber \]

donde:

$\overline{x}_1 $es el promedio del primer conjunto de datos
$\overline{x}_2 $es el promedio del segundo conjunto de datos
$n_1$es el número de mediciones en el primer conjunto de datos
$n_2$es el número de mediciones en el segundo conjunto de datos
$s_1$es la desviación estándar del primer conjunto de datos
\ (s_2) es la desviación estándar del segundo conjunto de datos
$t$es resultado de la prueba t; se relaciona con valores de la distribución t de Student

También tenga en cuenta que la varianza se define como el cuadrado de la desviación estándar.

Usando tablas de distribución t (muestra que se muestra a continuación), se puede determinar el nivel de confianza para las dos medias. Este nivel de confianza determina si las dos medias son significativamente diferentes. El nivel de confianza se puede encontrar con los grados de libertad para las mediciones y el valor t calculado anteriormente. El grado de libertad es igual a dos menos que el número total de mediciones de los dos conjuntos de datos, como se muestra a continuación:

\[D O F=n_{1}+n_{2}-2 \nonumber \]

La siguiente tabla es una imagen de una tabla de valores t, que también se puede encontrar (aquí):

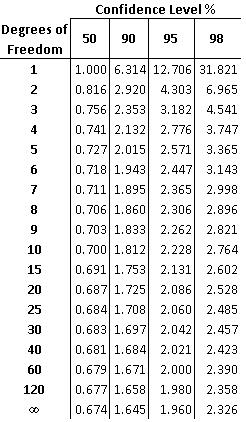
Por ejemplo, si tuvieras dos conjuntos de datos que suman 10 mediciones y calculaste un valor t de 2.305 el nivel de confianza sería del 95%. Esto significa que hay un 95% de probabilidad de que los dos conjuntos de datos sean estadísticamente diferentes y solo un 5% de probabilidad de que los dos conjuntos de datos sean estadísticamente similares. Además, los grados de libertad entre los valores enumerados en la tabla se pueden encontrar interpolando entre esos dos valores.

Tenga en cuenta que existen algunos inconvenientes a la hora de evaluar dos medios para ver si son significativos o no. Este problema proviene principalmente de la desviación estándar. Si digamos que un conjunto de valores tiene una cierta media x, pero la desviación estándar fue alta debido a que algunos números en pueden haber estado muy fuera del rango de la media. Esta desviación estándar puede implicar, a partir de la prueba t de estudiante, que la media x es significativamente diferente de la media de otro conjunto de datos, cuando en realidad puede no parecer tan diferente. De ahí que esto se tenga en cuenta al comparar dos medias utilizando la prueba t de Student.

Comparando dos medias verdaderas desconocidas (μ ₁ =? y μ ₂ =? ) con Desviaciones Estándar Desiguales Verdaderas Conocidas (\[\\sigma_1 \neq \sigma_2 \nonumber \])

La prueba z se utiliza cuando la diferencia entre una media muestral y la media poblacional es lo suficientemente grande como para ser estadísticamente significativa. La prueba t y la prueba z son esencialmente las mismas pero en la prueba z se conocen las medias reales de la población (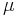 $mu\,$ ) y las desviaciones estándar ( 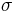$sigma\,$ ). Dado que la estimación de la diferencia en la desviación estándar utilizada aquí es sesgada, rara vez se utilizan dos pruebas z de muestra.

El estadístico z de dos muestras se describe por:

\[z=\frac{\text { Signal }}{\text { Noise }}=\frac{\bar{x}_{1}-\bar{x}_{2}}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}} \nonumber \]

donde:

$\overline{x}_1 $es el promedio del primer conjunto de datos
$\overline{x}_2 $es el promedio del segundo conjunto de datos
$n_1$es el número de mediciones en el primer conjunto de datos
$n_2$es el número de mediciones en el segundo conjunto de datos
$\sigma_1 $es la desviación estándar conocida de la primera población
$\sigma_2 $es la desviación estándar conocida de la segunda población

Se utiliza una tabla diferente para buscar la probabilidad de significación, consulte la tabla de puntuación Z. Si p < 0.05 (usando un intervalo de confianza del 95%), podemos declarar que existe una diferencia significativa. El valor p es la probabilidad de que la diferencia observada entre las medias sea causada por la variación del muestreo, o la probabilidad de que estas dos muestras provengan de la misma población.

Comparando dos medias verdaderas desconocidas (μ ₁ =? y μ ₂ =? ) con Desviaciones estándar verdaderas desconocidas (σ ₁ =? y σ ₂ =? )

Esto se conoce como el estadístico t de dos muestras, que se utiliza en la inferencia estadística para comparar las medias de dos poblaciones independientes, normalmente distribuidas, con desviaciones estándar verdaderas desconocidas. El estadístico t de dos muestras se describe por:

\[t=\frac{\text { Signal }}{\text { Noise }}=\frac{\bar{x}_{1}-\bar{x}_{2}}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}} \nonumber \]

Donde:

\[\\overline{x}_1 \nonumber \]es el promedio del primer conjunto de datos
\[\\overline{x}_2 \nonumber \]es el promedio del segundo conjunto de datos
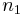$n_1\,$ es el número de mediciones en el primer conjunto de datos
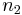$n_2\,$ es el número de mediciones en el segundo conjunto de datos
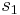$s_1\,$ es la desviación estándar del primer conjunto de datos
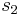$s_2\,$ es la desviación estándar del segundo conjunto de datos

Comparación de la Media de Diferencias para Datos Pareados

Esto se utiliza en el análisis estadístico para el caso donde se produce una sola media de una población cuando se recolectan dos variables cuantitativas en pares, y la información que deseamos de estos pares es la diferencia entre las dos variables.

Dos ejemplos de datos emparejados:

Cada unidad se mide dos veces. Las dos mediciones de los mismos datos se toman bajo condiciones variadas.
Unidades similares se emparejan antes del experimento o ejecución. Durante el experimento o ejecución cada unidad se coloca en diferentes condiciones.

El estadístico t de medias de diferencias se describe por:

\[t=\frac{\bar{d}}{\frac{s_{d}}{\sqrt{n}}} \nonumber \]

donde:

$\overline{d} $es la media de las diferencias para una muestra de las dos mediciones
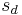$s_d\,$ es la desviación estándar de las diferencias muestreadas
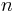$n\,$ es el número de mediciones en la muestra

Resumen de Pruebas de Media de Dos Muestras

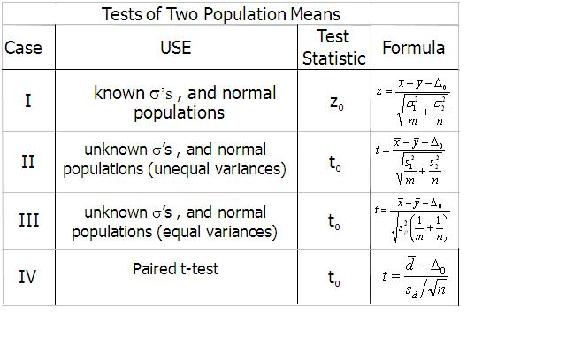
wo muestra media tests.jpg

Método Excel

En lugar de usar las tablas de distribución t para interpolar valores, a menudo es más fácil usar herramientas integradas en Excel. Las siguientes tres funciones se pueden utilizar para la mayoría de las situaciones comunes encontradas al comparar dos medias:

La función TDIST es útil cuando se ha calculado un valor t y se desea conocer la probabilidad de que el valor t sea significativo.
La función TINV es útil cuando conoces la probabilidad de significancia que te interesa, y deseas el valor t (esencialmente lo contrario de la función TDIST). Esto es útil si está diseñando un experimento y le gustaría determinar el número de ejecuciones experimentales necesarias para probar la diferencia de dos medias.
La función TTEST es útil si tienes dos conjuntos de datos y te gustaría saber la probabilidad de que la media de los dos conjuntos de datos sea significativamente diferente.

Función TDIST

La función TDIST tiene la sintaxis “=TDIST (x, deg_freedom, colas)”

Donde:

x es el valor t de la estadística
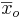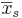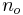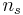deg_freedom es el número de grados de libertad del estadístico t. Para comparar medias muestrales $\ overline {x} _o$ y $\ overline {x} _s$ , con tamaños de muestra $n_o\,$ y $n_s\,$ respectivamente, tiene 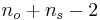$n_o + n_s - 2\,$ grados de libertad.
colas es el número de colas a sumar para la probabilidad. Si la hipótesis nula es una igualdad, se utilizarán 2 colas. Si la hipótesis nula es una desigualdad, se utilizará 1 cola.

La salida de la función es la probabilidad fraccionaria de la distribución t de Students. Por ejemplo, si la función devolviera un valor de 0.05, éste correspondería a un nivel de confianza del 95% o equivalentemente (1 - 0.05) para rechazar la hipótesis nula.

Función TINV

La función TINV tiene la sintaxis “=TINV (probalilidad, deg_freedom)”

donde:

probabilidad es la probabilidad fraccionaria de la distribución t de Students. Esto es idéntico a la salida de la función “TDIST”.
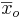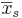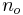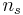deg_freedom es el número de grados de libertad del estadístico t. Para comparar medias muestrales $\ overline {x} _o$ y $\ overline {x} _s$ , con tamaños de muestra $n_o\,$ y $n_s\,$ respectivamente, tiene 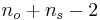$n_o + n_s - 2\,$ grados de libertad.

La salida de la función es el valor t de la distribución t de Student.

Función TTEST

La función TTEST tiene la sintaxis “=TTEST (array 1, array 2, tails, type)”

donde:

matriz 1 es el primer conjunto de datos
matriz 2 es el segundo conjunto de datos
colas es el número de colas a sumar para probabilidad (1 o 2). Si la hipótesis nula es una igualdad se utilizarán 2 colas, si la hipótesis nula es una desigualdad se utilizará 1 cola.
tipo es el tipo de prueba t a realizar los valores que corresponden a cada tipo de prueba se enumeran a continuación.

Si tipo es igual | Esta prueba se realiza 1 | Pareado 2 | Varianza igual de dos muestras (homoscedástica) 3 | Varianza desigual de dos muestras (heteroscedástica)

Para nuestros fines solo nos ocuparemos del tipo = 3. Esto corresponde a varianza desigual (conjuntos de datos independientes). Los otros dos tipos son útiles y pueden resultar interesantes para los curiosos, pero están más allá de nuestro alcance.

Alternativamente, si no te gusta Excel, un sitio web ubicado aquí hará el cálculo TTEST por ti.

La salida de la función es la probabilidad fraccionaria de la distribución t de Student. Por ejemplo, si la función devolviera un valor de 0.05, éste correspondería a un nivel de confianza del 95% o equivalentemente (1 - 0.05) para rechazar la hipótesis nula.

Esta función es muy útil cuando se conocen los conjuntos de datos de los dos medios a comparar.

Funcionó Ejemplo 1

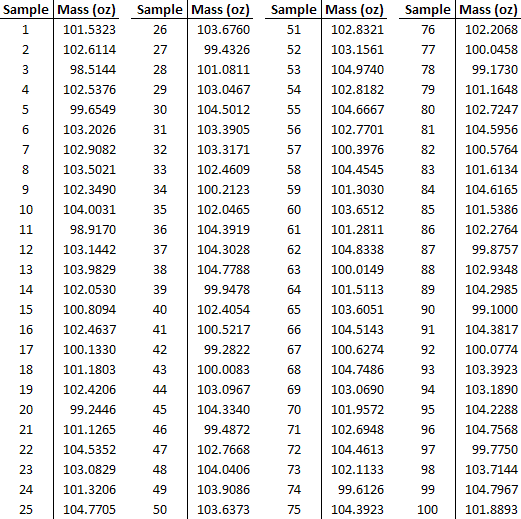
Eres ingeniero de calidad de producto en una empresa que fabrica detergente para ropa en polvo en cajas de 100 onzas. Usted es el encargado de determinar si el producto cumple con las especificaciones que la compañía promete al cliente. En el pasado, 100 muestras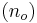 $\ izquierda (n_o\ derecha)$ del proceso establecieron condiciones normales de proceso. Los datos se dan a continuación. Tenga en cuenta que pesar muestras usando una báscula imprecisa no afecta sus resultados. También supongamos que las desviaciones estándar son lo suficientemente cercanas como para agruparlas.

Muestrea aleatoriamente 25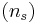 $\ izquierda (n_s\ derecha)$ de los productos y obtienes los siguientes datos:

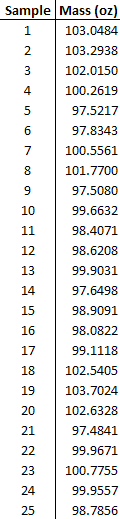
Los datos también se pueden encontrar en la primera pestaña de este archivo Excel: Archivo de Datos

¿El proceso que se ejecuta es significativamente diferente de lo normal con 95% de confianza? En este ejemplo, no utilice funciones integradas de Excel.

Solución

Utilizando los datos, el proceso normal produce una masa promedio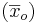 $\ izquierda (\ overline {x} _o\ derecha)$ del producto de 102.37 y una varianza 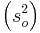$\ izquierda (s_o^2\ derecha)$ de 3.17.

La muestra tiene una masa promedio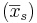 $\ izquierda (\ overline {x} _s\ derecha)$ de 100.00 con una varianza 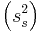$\ izquierda (s_s^2\ derecha)$ de 4.00.

Estos se calcularon utilizando la función PROMEDIO y la función VAR en Excel. Consulte la segunda pestaña de este archivo Excel para mayor explicación: Ejemplo 1

La hipótesis nula es que las medias son idénticas y la diferencia entre las dos medias se debe puramente al azar.

Usando la prueba t:

\[t=\frac{\bar{x}_{o}-\bar{x}_{s}}{\sqrt{\frac{s_{o}^{2}\left(n_{o}-1\right)+s_{s}^{2}\left(n_{s}-1\right)}{n_{o}+n_{s}-2}}} \sqrt{\frac{n_{o} n_{s}}{n_{o}+n_{s}}} \nonumber \]

\[t=\frac{102-100}{\sqrt{\frac{3(100-1)+4(25-1)}{100+25-2}}} \sqrt{\frac{25 * 100}{25+100}}=5.00 \nonumber \]

Mirando la tabla que se reproduce a continuación para referencia:

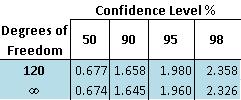
El número de grados de libertad es:

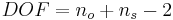
$DOF = n_o + n_s - 2\,$

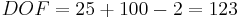
$DOF = 25 + 100 - 2 = 123\,$

El valor t correspondiente al nivel de confianza del 95% a 123 grados de libertad se encuentra entre 1.960 y 1.980. Dado que el valor t calculado, 5.00, es mucho mayor que 1.980, la hipótesis nula es rechazada al nivel de confianza del 95%.

Se concluye que las dos medias son significativamente diferentes. Por lo tanto, el proceso no se ejecuta normalmente y es el momento de solucionar problemas para encontrar los problemas que ocurren en el sistema.

Funcionó Ejemplo 2

El mismo problema que “Ejemplo resuelto 1”. En su lugar, utilice la función TTEST en Excel.

Solución

La solución también se puede ver en la tercera pestaña de este archivo Excel: Ejemplo 2

Usando la función TTEST, con colas = 2 y tipo de prueba = 3, la función da un valor de prueba T de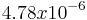 $4.78 x 10^ {-6}\,$ .

Dado que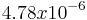 $4.78 x 10^ {-6}\,$ es menor de 0.05 (a partir de nuestro nivel de confianza del 95%) podemos concluir una vez más que podemos rechazar la hipótesis nula.

Ejercicio$\PageIndex{1}$

Si hay dos conjuntos de datos, uno con 15 mediciones y otro con 47 mediciones, ¿cuántos grados de libertad ingresarías en las funciones de Excel?

Contestar

El número de grados de libertad se calcula de la siguiente manera:

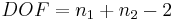
$DOF = n_1 + n_2 - 2\,$

donde n ₁ es el número de mediciones en el primer conjunto de datos y n ₂ es el número de mediciones en el segundo conjunto de datos.

Por lo tanto,

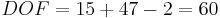
$DOF = 15 + 47 - 2 = 60\,$

la respuesta es d.

Ejercicio$\PageIndex{2}$

¿Qué significa la afirmación “Precisa dentro del 95% de confianza”?

El promedio del conjunto de datos es estadísticamente igual al valor verdadero dentro del 95%
El valor es el promedio más o menos 95%
El promedio es estadísticamente igual al valor verdadero dentro del 5%

Contestar: c

Referencias

“Comparación de Dos Medios”. Estado.Yale.Edu. Yale. 19 nov. 2006 < http://www.stat.yale.edu/Courses/1997-98/101/meancomp.htm >.
Archivo de Ayuda de Excel. Microsoft 2006.
Harris, Daniel C. Explorando el Análisis Químico. 3a ed. Nueva York: W. H. Freeman and Company, 2005. 77-151.
Woolf, Peter, et al. Estadística e Imprimación de Probabilidad para Biólogos Computacionales. Instituto Tecnológico de Massachusetts. BE 490/Bio 7.91. Primavera 2004. 52-68.
“Prueba Z”. Wikipedia. es.wikipedia.org/wiki/Z-test

Search

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)