13.12: Análisis factorial y ANOVA

Inventado por primera vez a principios del siglo XX por el psicólogo Charles Spearman, el análisis factorial es el proceso por el cual se simplifica un complicado sistema de muchas variables definiéndolo completamente con un menor número de “factores”. Si estos factores pueden ser estudiados y determinados, pueden ser utilizados para predecir el valor de las variables en un sistema. Un ejemplo simple sería usar la inteligencia de una persona (un factor) para predecir sus puntuaciones verbales, cuantitativas, escritas y analíticas en las GRE (variables).

El análisis de varianza (ANOVA) es el método utilizado para comparar mediciones continuas para determinar si las mediciones se muestrean a partir de la misma distribución o de diferentes distribuciones. Se trata de una herramienta analítica utilizada para determinar la significancia de los factores en las mediciones al observar la relación entre una “variable de respuesta” cuantitativa y un “factor” explicativo propuesto. Este método es similar al proceso de comparación de la diferencia estadística entre dos muestras, en que invoca el concepto de prueba de hipótesis. Sin embargo, en lugar de comparar dos muestras, una variable se correlaciona con uno o más factores explicativos, típicamente usando el estadístico F. A partir de esta estadística F, se puede calcular el valor P para ver si la diferencia es significativa. Por ejemplo, si el valor P es bajo (valor P <0.05 o valor P <0.01 - esto depende del nivel de significancia deseado), entonces hay una baja probabilidad de que los dos grupos sean iguales. El método es altamente versátil ya que puede ser utilizado para analizar sistemas complicados, con numerosas variables y factores. En este artículo, discutiremos los cómputos involucrados en ANOVA de factor único, de dos factores: sin réplicas y de dos factores: con réplicas. A continuación, se muestra una breve descripción de los diferentes tipos de ANOVA y algunos ejemplos de cuándo se pueden aplicar.

Descripción general y ejemplos de tipos de ANOVA

Tipos de ANOVA

ANOVA de factor único (unidireccional):

El ANOVA unidireccional se utiliza para probar la varianza entre dos o más grupos independientes de datos, en el caso de que la varianza dependa de un solo factor. Se emplea con mayor frecuencia cuando hay al menos tres grupos de datos, de lo contrario una prueba t sería un análisis estadístico suficiente.

ANOVA de dos factores (bidireccional):

Se utiliza ANOVA bidireccional en el caso de que la varianza dependa de dos factores. Hay dos casos en los que se puede emplear ANOVA bidireccional:

• Datos sin réplicas: se utilizan al recopilar un solo punto de datos para una condición especificada
• Datos con réplicas: se utilizan al recopilar múltiples puntos de datos para una condición especificada (el número de réplicas debe especificarse y debe ser el mismo entre los grupos de datos)

Cuándo usar cada tipo de ANOVA

• Ejemplo: Existen tres reactores idénticos (R1, R2, R3) que generan el mismo producto.

• ANOVA unidireccional: Se desea analizar la varianza del rendimiento del producto en función del número del reactor.
• ANOVA bidireccional sin repeticiones: Se desea analizar la varianza del rendimiento del producto en función del número de reactores y la concentración de catalizador.
• ANOVA bidireccional con repeticiones: Para cada concentración de catalizador, se tomaron datos por triplicado. Se desea analizar la varianza del rendimiento del producto en función del número de reactores y la concentración de catalizador.

ANOVA es un modelo lineal

Aunque ANOVA te dirá si los factores son significativamente diferentes, lo hará de acuerdo a un modelo lineal. El ANOVA siempre asume un modelo lineal, es importante considerar interacciones no lineales fuertes que el ANOVA puede no incorporar a la hora de determinar la significancia. El ANOVA funciona asumiendo cada observación como media general + efecto medio + ruido. Si hay una relación no lineal entre estos (por ejemplo, si la diferencia entre la columna 1 y la columna 2 de la misma fila es esa columna2 = column1^2), entonces existe la posibilidad de que ANOVA no lo atrape.

Términos Clave

Antes de una explicación adicional, por favor revise los términos a continuación, que se utilizan a lo largo de este Wiki.

Comparación de las medias de la muestra usando la prueba F

La Prueba F es la relación de las varianzas de la muestra. El estadístico F y la prueba F correspondiente se utilizan en ANOVA de factor único para fines de prueba de hipótesis.

Hipótesis nula (H _o): todas las medias muestrales derivadas de diferentes factores son iguales

Hipótesis alternativa (H _a): las medias de la muestra no son todas iguales

Para utilizar la prueba F son necesarias varias suposiciones:

• Las muestras son independientes y aleatorias
• La distribución de la variable respuesta es una curva normal dentro de cada población
• Las diferentes poblaciones pueden tener diferentes medios
• Todas las poblaciones tienen la misma desviación estándar

Introducción a la estadística F

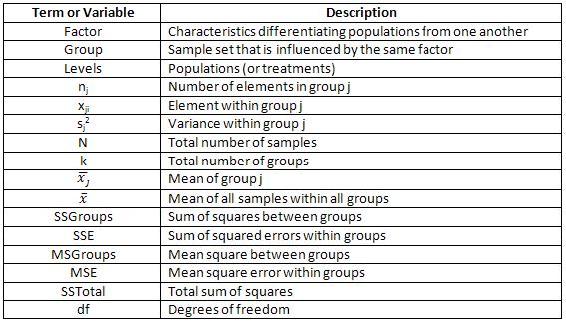
El estadístico F es la razón de dos estimaciones de varianza: la varianza entre grupos dividida por la varianza dentro de grupos. Cuanto mayor sea el estadístico F, más probable es que la diferencia entre muestras se deba al factor que se está probando, y no solo a la variación natural dentro de un grupo. Se puede utilizar una tabla estandarizada para encontrar F _crítica para cualquier sistema. F _crítico dependerá de alfa, que es una medida del nivel de confianza. Por lo general, se utiliza un valor de alfa = 0.05, que corresponde a 95% de confianza. Si F _observó > F _crítico, concluimos con 95% de confianza que la hipótesis nula es falsa. Para una explicación de cómo leer una Tabla F, consulte Interpretación del estadístico F (abajo). De manera similar, las tablas F también se pueden usar para determinar el valor p para un conjunto de datos dado. El valor p para un conjunto de datos dado es la probabilidad de que se pueda obtener este conjunto de datos si la hipótesis nula fuera cierta: es decir, si los resultados se debían estrictamente a la casualidad. Cuando H _o es verdadero, el estadístico F tiene una distribución F.

Distribuciones F

La distribución F es importante para el ANOVA, ya que se utiliza para encontrar el valor p para una prueba F de ANOVA. La distribución F surge de la relación de dos distribuciones de Chi cuadrado. Así, esta familia tiene un numerador y denominador grados de libertad. (Para obtener información sobre la prueba de Chi cuadrado, haga clic aquí.) Cada función de esta familia tiene una distribución sesgada y un valor mínimo de cero.

Figura 1 - Distribución F con alfa y F _crítica indicada

Análisis de varianza de factor único

En el caso del análisis de un solo factor, también llamado clasificación única o unidireccional, se varía un factor al tiempo que se observa el resultado en el conjunto de variables dependientes. Estas variables dependientes pertenecen a un conjunto específico de valores relacionados y por lo tanto, se espera que los resultados estén relacionados.

En esta sección se describirán algunos de los detalles computacionales para el estadístico F en ANOVA unidireccional. Aunque estas ecuaciones proporcionan una visión del concepto de análisis de varianza y cómo se construye la prueba F, no es necesario aprender fórmulas ni hacer este análisis a mano. En la práctica, las computadoras siempre se utilizan para hacer ANOVA unidireccional

Configuración de una Tabla de Análisis de Varianza

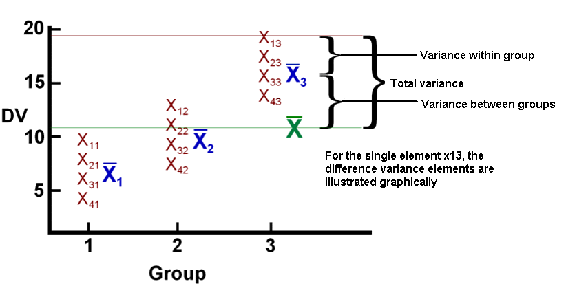
El concepto fundamental en el análisis de varianza unidireccional es que la variación entre los puntos de datos en todas las muestras se puede dividir en dos categorías: variación entre medias de grupo y variación entre puntos de datos en un grupo. La teoría para el análisis de la varianza deriva de una ecuación simple, afirmando que la varianza total es igual a la suma de la varianza entre grupos y la variación dentro de los grupos,

Variación total = variación entre grupos + variación dentro de los grupos

Se utiliza una tabla de análisis de varianza para organizar los puntos de datos, indicando el valor de una variable de respuesta, en grupos según el factor utilizado en cada caso. Por ejemplo, el Cuadro 1 es una tabla ANOVA para comparar la cantidad de peso perdido en un periodo de tres meses por personas que hacen dieta en diversos programas de pérdida de peso.

Tabla 1 - Cantidad de peso perdido por personas que hacen dieta en diversos programas durante un periodo de 3 meses

Programa 1	Programa 2	Programa 3
7	9	15
9	11	12
5	7	18
7

Una pregunta razonable es, ¿se puede usar el tipo de programa (un factor) para predecir la cantidad de peso que una persona a dieta perdería en ese programa (una variable de respuesta)? O, en otras palabras, ¿algún programa es superior a los demás?

Medición de la variación entre grupos

La variación entre medias de grupo se mide con una suma ponderada de diferencias cuadradas entre las medias de la muestra y la media general de todos los datos. Cada diferencia cuadrada se multiplica por el tamaño de muestra de grupo apropiado, ni, en esta suma. Esta cantidad se denomina suma de cuadrados entre grupos o Grupos SS.

\[\text { SSGroups }=n_{1}\left(x_{1}-x\right)^{2}+n_{2}\left(x_{2}-x\right)^{2}+\ldots+n_{k}\left(x_{k}-x\right)^{2}=\sum_{\text {yrсups }} n_{j}\left(\bar{x}_{j j}-\bar{x}^{\prime 2}\right.\nonumber \]

El numerador del estadístico F para comparar medias se denomina el cuadrado medio entre grupos o Grupos MS, y se calcula como -

\[\text { MSGroups }=\frac{\text { SSGroups }}{k-1}\nonumber \]

Medición de la variación dentro de grupos

Para medir la variación entre los puntos de datos dentro de los grupos, busque la suma de las desviaciones cuadradas entre los valores de los datos y la media de la muestra en cada grupo, y luego agregue estas cantidades. Esto se llama la suma de errores cuadrados, SSE, o suma de cuadrados dentro de los grupos.

\[S S E=\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}+\ldots+\left(n_{k}-1\right) s_{k}^{2}=\sum_{\text {allgroups }}\left(n_{j}-1\right) s_{j}^{2}\nonumber \]

donde

\[s_{j}^{2}=\sum_{\text {groupj }} \frac{\left(x_{i j}-\bar{x}_{j}\right)^{2}}{n_{j}-1}=\nonumber \]

y es la varianza dentro de cada grupo.

El denominador del estadístico F se denomina error cuadrático medio, MSE, o cuadrados medios dentro de los grupos. Se calcula como

\[M S E=\frac{S S E}{N-k}=\frac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}+\ldots+\left(n_{k}-1\right) s_{k}^{2}}{n_{1}+n_{2}+\ldots+n_{k}-k}\nonumber \]

El MSE es simplemente un promedio ponderado de las varianzas de la muestra para los k grupos. Por lo tanto, si todos los n _i son iguales, MSE es simplemente el promedio de las k varianzas de la muestra. La raíz cuadrada de MSE (s _p), denominada desviación estándar agrupada, estima la desviación estándar poblacional de la variable de respuesta (tenga en cuenta que se supone que todas las muestras que se comparan tienen la misma desviación estándar σ).

Medición de la variación total

La variación total en todas las muestras combinadas se mide calculando la suma de las desviaciones cuadradas entre los valores de los datos y la media de todos los puntos de datos. Esta cantidad es referida como la suma total de cuadrados o SS Total. La suma total de cuadrados también puede denominarse SSTO. Una fórmula para la suma de las diferencias al cuadrado de la media general es

\[\text { SSTotal }=\sum_{\text {values }}\left(x_{i j}-\bar{x}\right)^{2}\nonumber \]

donde x _ij representa la jésima observación dentro del grupo i-ésimo, y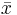 es la media de todos los valores de datos observados. Finalmente, la relación entre SS Total, SS Grupos y SS Error es

SS Total = SS Grupos + Error SS

En general, la relación entre la variación total, la variación entre grupos y la variación dentro de un grupo se ilustra en la Figura 2.

Figura 2: Ilustración visual de la varianza en ANOVA, adaptada de www.uwsp.edu/psych/stat/12/anova-1w.htm

A continuación se proporciona una tabla general para realizar los cálculos ANOVA unidireccionales necesarios para calcular el estadístico F

Tabla 2 - Tabla ANOVA unidireccional

Fuente	Grados de Libertad	Suma de Cuadrados	Suma media de cuadrados	Estadística F
Entre grupos	k-1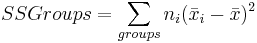
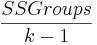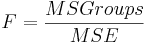Dentro de los grupos (error)	N-k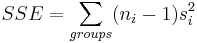
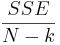Total	N-1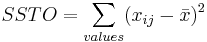

Interpretación del estadístico F

Una vez que se ha encontrado el estadístico F, se puede comparar con un valor F crítico de una tabla, como esta: Tabla F. Esta tabla F se calcula para un valor de alfa = 0.05, indicando un nivel de confianza del 95%. Esto significa que si F _observado es mayor que F _crítico de la tabla, entonces podemos rechazar la hipótesis nula y decir con 95% de confianza que la varianza entre grupos no se debe a la casualidad aleatoria, sino a la influencia de un factor probado. Las tablas también están disponibles para otros valores de alfa y se pueden usar para encontrar una probabilidad más exacta de que la diferencia entre grupos sea (o no) causada por azar azar.

Encontrar el valor F crítico

En esta Tabla F, la primera fila de la tabla F es el número de grados de entre grupos (número de grupos - 1), y la primera columna es el número de grados de libertad dentro de los grupos (número total de muestras - número de grupos).

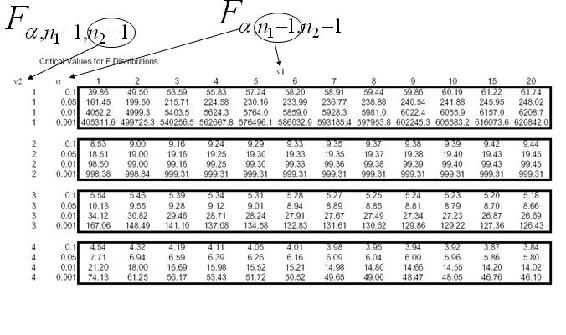
Para el ejemplo de dieta en la Tabla 1, el grado de libertad entre grupos es (3-1) = 2 y y el grado de libertad dentro de los grupos es (13-3) = 10. Así, el valor crítico de F es de 4.10.

Cálculo del intervalo de confianza del 95% para las medias de la población

Es útil conocer el intervalo de confianza en el que se reportan las medias de los diferentes grupos. La fórmula general para calcular un intervalo de confianza es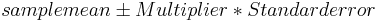. Debido a que se supone que todas las poblaciones tienen la misma desviación estándar se 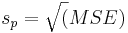puede utilizar para estimar la desviación estándar dentro de cada grupo. Si bien se asume que la desviación estándar de la población es la misma, el error estándar y el multiplicador pueden ser diferentes para cada grupo, debido a diferencias en el tamaño del grupo y grados de libertad. El error estándar de una media muestral es inversamente proporcional a la raíz cuadrada del número de puntos de datos dentro de la muestra. Se calcula como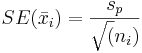. El multiplicador se determina usando una distribución t donde los grados de libertad se calculan como df = n-K. Por lo tanto, Insertformulaaquí el intervalo de confianza para una media poblacional es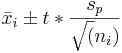. Se pueden encontrar más detalles sobre los intervalos de confianza en Comparación de dos medias

Un ejemplo para usar el análisis factorial es el siguiente:

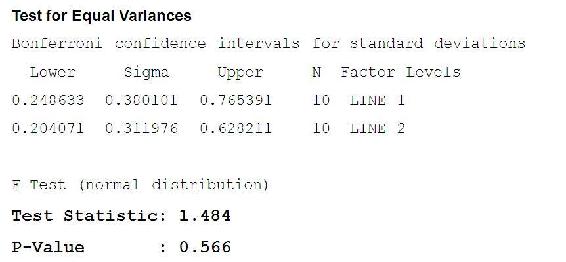
Tienes dos líneas de montaje. Supongamos que toma muestras de 10 partes de las dos líneas de montaje. Ho: s1 ² = s2x ² Ha: las varianzas no son iguales ¿Las dos líneas producen salidas similares? Asumir a=0.05 F _.025,9,9 = 4.03 F _1-.025,9,9 =?

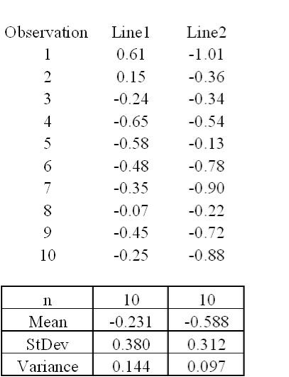
¿Son diferentes las varianzas?

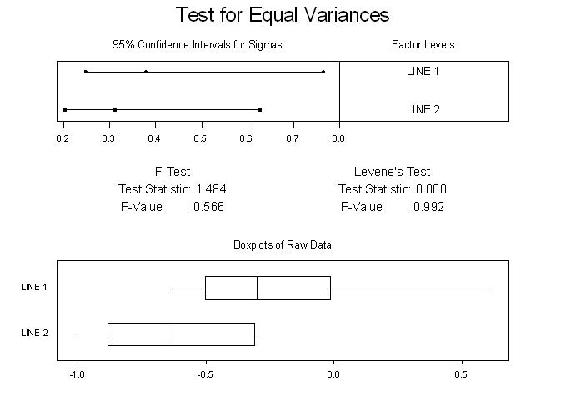
¿Cómo probaríamos si los medios son diferentes?

Análisis de varianza de dos factores

Se utiliza un análisis de varianza de dos factores o de dos vías para examinar cómo dos variables categóricas cualitativas (macho/hembra) afectan la media de una variable de respuesta cuantitativa. Por ejemplo, un psicólogo podría querer estudiar cómo el tipo y el volumen de la música de fondo afectan la productividad de los trabajadores. Alternativamente, un economista tal vez esté interesado en determinar el efecto del género y la raza en el ingreso medio. En ambos ejemplos, existe interés en el efecto de cada factor explicativo separado, así como el efecto combinado de ambos factores.

Supuestos

Para utilizar el ANOVA bidireccional, se requieren los siguientes supuestos:

• Las muestras deben ser independientes.
• Las varianzas poblacionales deben ser iguales.
• Los grupos deben tener el mismo tamaño de muestra. Las poblaciones de las que se obtuvieron las muestras deben estar normalmente distribuidas (o al menos aproximadamente).
• Se supone que la hipótesis nula es verdadera.

La hipótesis nula es la siguiente:

• Las medias poblacionales para el primer factor tienen que ser iguales. Esto es similar al ANOVA unidireccional para el factor de fila.
• Las medias poblacionales para el segundo factor también deben ser iguales. Esto es similar al ANOVA unidireccional para el factor columna.
• No hay interacción entre los dos factores. Esto es similar a realizar una prueba de independencia usando tablas de contingencia.

Más simplemente, la hipótesis nula implica que las poblaciones son todas similares y que cualquier diferencia en las poblaciones es causada por el azar, no por la influencia de un factor. Después de realizar ANOVA bidireccional será posible analizar la validez de este supuesto.

Términos utilizados en ANOVA bidireccional

La interacción entre dos factores es la parte más singular de un análisis bidireccional del problema de varianza. Cuando dos factores interactúan, el efecto sobre la variable de respuesta depende del valor del otro factor. Por ejemplo, la afirmación de que el sobrepeso provocó mayores aumentos en la presión arterial para los hombres que en las mujeres describe una interacción. En otras palabras, el efecto del peso (factor) sobre la presión arterial (respuesta) depende del género (factor).

El término efecto principal se utiliza para describir el efecto general de una sola variable explicativa. En el ejemplo musical, el efecto principal del factor “volumen musical” es el efecto sobre la productividad promediada sobre todo tipo de música. Claramente, el efecto principal puede no ser siempre útil si se desconoce la interacción.

En un análisis de varianza bidireccional, se construyen tres estadísticas F. Uno se utiliza para probar la significancia estadística de la interacción, mientras que los otros dos se utilizan para probar la significancia de los dos efectos principales separados. También se reporta el valor p para cada estadístico F: generalmente se usa un valor p de <.05 para indicar significancia. Cuando se encuentra que un factor F tiene significancia estadística, se considera un efecto principal. El valor p también se utiliza como indicador para determinar si los dos factores tienen una interacción significativa cuando se consideran simultáneamente. Si un factor depende fuertemente del otro, el estadístico F para el término de interacción tendrá un valor p bajo. Un ejemplo de salida del análisis bidireccional de varianza de datos de propina de restaurante se da en la Tabla 4.

Tabla 4 - Análisis bidireccional de varianza de los datos de propina de restaurante

Fuente	DF	Adj SS	Adj MS	Estadística F	Valor P
Mensaje	1	14.7	14.7	.13	.715
Sexo	1	2602.0	2602.0	23.69	0.00
Interacción	1	438.7	438.7	3.99	.049
Error	85	9335.5	109.8
Total	88	12407.9

En este caso, los factores que se estudian son el sexo (masculino o femenino) y el mensaje en el recibo (:-) o ninguno). Los valores p de la última columna son la información más importante contenida en esta tabla. Un valor p más bajo indica un mayor nivel de significancia. El mensaje tiene un valor de significación de .715. Esto es mucho mayor que .05, el intervalo de confianza del 95%, lo que indica que este factor no tiene significancia (ninguna correlación fuerte entre presencia de mensaje y cantidad de tip). La razón por la que esto ocurre es que existe una relación entre el mensaje y el sexo del mesero. El término de interacción, que fue significativo con un valor de p= 0.049, mostró que dibujar una cara feliz aumentó la punta para las mujeres pero la disminuyó para los hombres. El efecto principal del sexo de camarero (con un valor p de aproximadamente 0) muestra que existe una diferencia estadística en las propinas promedio para hombres y mujeres.

Cálculos de ANOVA bidireccional

Al igual que en el análisis ANOVA unidireccional, la herramienta principal utilizada son las sumas cuadradas de cada grupo. El ANOVA bidireccional se puede dividir entre dos tipos diferentes: con repetición y sin repetición. Con repetición significa que cada caso se repite un número determinado de veces. Para el ejemplo anterior eso significaría que el :-) se le dio a las hembras 10 veces y a los machos 10 veces, y no se le dio ningún mensaje a las hembras 10 veces y a los machos 10 veces

Usando los valores SS como inicio, se calculan las estadísticas F para ANOVA de dos vías con repetición usando el gráfico de abajo donde a es el número de niveles del efecto principal A, b es el número de niveles del efecto principal B y n es el número de repeticiones.

Fuente	SS	DF	Adj MS	Estadística F
Efecto Principal A	De los datos dados	a-1	SS/dF	MS (A) /MS (W)
Efecto Principal B	De los datos dados	b-1	SS/dF	MS (B) /MS (W)
Efecto de interacción	De los datos dados	(a-1) (b-1)	SS/dF	MS (A*B) /MS (W)
Dentro	De los datos dados	ab (n-1)	SS/dF
Total	suma de otros	abn-1

Sin repetición significa que hay una lectura por cada caso. Por ejemplo es que estabas investigando si la diferencia en el rendimiento es o no más significativa con base en el día en que se tomaron las lecturas o el reactor del que se tomaron las lecturas tendrías una lectura para el Reactor 1 el lunes, una lectura para el Reactor 2 el lunes etc... Los resultados para ANOVA de dos vías sin repetición son ligeramente diferentes en que no se mide el efecto de interacción y la fila interna se reemplaza por una fila de error similar (pero no igual). Los cálculos necesarios se muestran en la tabla siguiente.

Fuente	SS	DF	MS	Estadística F
Efecto Principal A	De los datos dados	a-1	SS/dF	MS (A) /MS (E)
Efecto Principal B	De los datos dados	b-1	SS/dF	MS (B) /MS (E)
Error	De los datos dados	(a-1) (b-1)	SS/dF
Total	suma de otros	ab-1

Estos cálculos casi nunca se hacen a mano. En esta clase usualmente usarás Excel o Mathematica para crear estas tablas. Las secciones que describen cómo usar estos programas se encuentran más adelante en este capítulo.

Otros métodos de comparación

Desafortunadamente, las condiciones para usar la prueba F de ANOVA no se mantienen en todas las situaciones. En esta sección, varios otros métodos que no se basan en desviaciones estándar de población iguales o distribución normal. Es importante darse cuenta de que ningún método de análisis factorial es apropiado si los datos aportados no son representativos del grupo en estudio.

Hipótesis sobre las medianas

En general, es mejor construir hipótesis sobre una mediana poblacional, en lugar de la media. El uso de la mediana explica que la muestra esté sesgada en función de valores atípicos extremos. También se deben utilizar hipótesis medianas para tratar variables ordinales (variables que solo se describen como mayores o menores que otras y no tienen un valor preciso). Cuando se comparan varias poblaciones, las hipótesis se establecen como -

H ₀: Las medianas de población son iguales
H _a: Las medianas de población no son todas iguales

Prueba de Kruskal-Wallis para comparar medianas

La Prueba de Kruskal-Wallis proporciona un método de comparación de medianas mediante la comparación de las clasificaciones relativas de los datos en las muestras observadas. Por lo tanto, esta prueba se conoce como prueba de rango o prueba no paramétrica porque la prueba no hace suposiciones sobre la distribución de datos.

Para realizar esta prueba, los valores en el conjunto de datos totales se clasifican primero de menor a mayor, siendo 1 más bajo y N siendo el más alto. Se promedian los rangos de los valores dentro de cada grupo, y el estadístico de prueba mide la variación entre los rangos promedio para cada grupo. Un valor p se puede determinar encontrando la probabilidad de que la variación entre el conjunto de promedios de rango para los grupos sea tan grande o mayor como lo es si la hipótesis nula es verdadera. Puede encontrar más información sobre la prueba de Kruskal-Wallis [aquí].

Prueba de mediana del estado de ánimo para comparar medianas

Otra prueba no paramétrica utilizada para comparar medianas poblacionales es la Prueba de Mediana de Mood. También llamada Prueba de Puntajes de Signos, esta prueba implica múltiples pasos.

1. Calcular la mediana (M) utilizando todos los puntos de datos de cada grupo del estudio
2. Crear una tabla de contingencia de la siguiente manera

	A	B	C	Total
Número de valores mayores que M
Número de valores menores o iguales a M

3. Calcule el valor esperado para cada conjunto de datos usando la siguiente fórmula:

\[\text { expected }=\frac{(\text { rowtotal })(\text { columntotal })}{\text { grandtotal }}\nonumber \]

4. Calcular el valor de chi-cuadrado usando la siguiente fórmula

\[\chi=\frac{(\text { actual - expected })^{2}}{\text { expected }}\nonumber \]

Se utiliza un estadístico chi-cuadrado para tablas bidireccionales para probar la hipótesis nula de que las medianas de la población son todas iguales. La prueba equivale a probar si las dos variables están o no relacionadas.

ANOVA y Análisis Factorial en Control de Procesos

El ANOVA y el análisis factorial se utilizan normalmente en el control de procesos con fines de resolución Cuando surge un problema en un sistema de control de procesos, estas técnicas pueden ser utilizadas para ayudar a resolverlo. Un factor puede definirse como una sola variable o proceso simple que tiene un efecto en el sistema. Por ejemplo, un factor puede ser la temperatura de una corriente de entrada, el caudal de refrigerante o la posición de una válvula específica. Cada factor puede analizarse individualmente para determinar el efecto que el cambio de entrada tiene en el sistema de control de procesos en su conjunto. La variable de entrada puede tener un efecto grande, pequeño o nulo sobre lo que se está analizando. La cantidad que la variable de entrada afecta al sistema se denomina “carga de factores”, y es una medida numérica de cuánto influye una variable específica en el sistema o en la variable de salida. En general, cuanto mayor es la carga del factor para una variable, mayor es el efecto que tiene sobre la variable de salida.

Una ecuación simple para esto sería:

Salida = f ₁ * entrada ₁ + f ₂ * entrada ₂ +... + f _n * entrada _n

donde f _n es el factor de carga para la ^n-ésima entrada.

El análisis factorial se utiliza en este estudio de caso para determinar el ensuciamiento en un reboiler de planta de alcohol. Este artículo proporciona algunas ideas adicionales sobre cómo se utiliza el análisis factorial en una situación industrial.

Uso de Mathematica para realizar ANOVA

Mathematica se puede utilizar para análisis factoriales unidireccionales y bidireccionales. Antes de que esto se pueda hacer, el paquete ANOVA debe cargarse en Mathematica usando el siguiente comando:

Necesidades [“ANOVA`”]

Una vez que se ejecuta este comando, se puede utilizar el comando 'ANOVA'.

Análisis factorial unidireccional

La forma básica del comando 'ANOVA' para realizar un análisis factorial unidireccional es la siguiente:

ANOVA [data]

Un conjunto de datos de ejemplo con cinco elementos se vería así:

ANOVA [

ParseError: EOF expected (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/13:_Estadísticas_y_antecedentes_probabilísticos/13.12:_Análisis_factorial_y_ANOVA), /content/body/div[8]/div[1]/p[3]/span, line 1, column 2

]

Una tabla de salida que incluye los grados de libertad, la suma de los cuadrados, la suma media de los cuadrados, la estadística F y el valor P para el modelo, el error y el total se mostrará cuando se ejecute esta línea. Una lista de medias de celda para cada modelo se mostrará debajo de la tabla.

Análisis factorial bidireccional

La forma básica del comando 'ANOVA' para realizar un análisis factorial bidireccional es la siguiente:

ANOVA [data, model, vars]

Un conjunto de datos de ejemplo con siete elementos se vería así:

ANOVA [

ParseError: EOF expected (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/13:_Estadísticas_y_antecedentes_probabilísticos/13.12:_Análisis_factorial_y_ANOVA), /content/body/div[8]/div[2]/p[3]/span, line 1, column 2

, {x, y}, {x, y}]

Una tabla de salida aparecerá similar a la que se muestra en el análisis unidireccional excepto que habrá una fila de estadísticas para cada variable (es decir, x, y).

ANOVA en Microsoft Excel 2007

Para acceder a la herramienta de análisis de datos ANOVA, instale el paquete:

1. Haga clic en el botón de Microsoft Office (círculo grande con logotipo de Office)
2. Haga clic en 'Opciones de Excel'
3. Haga clic en 'Complementos' en el lado izquierdo
4. En el cuadro desplegable administrar en la parte inferior de la ventana, seleccione 'Complementos de Excel'
5. Haga clic en 'Ir... '
6. En la ventana Complementos, marque la casilla Herramientas de análisis y haga clic en 'Aceptar'

Para utilizar este paquete:

1. Haga clic en la pestaña 'Datos' y seleccione 'Análisis de datos'
2. Elija el tipo de ANOVA deseado- 'Anova: Factor Único', 'Anova: Dos Factores con Replicación', o 'Anova: Dos Factores sin Replicación' (vea la nota a continuación para saber cuándo usar la replicación)
3. Seleccione los puntos de datos deseados incluyendo etiquetas de datos en la parte superior de las columnas correspondientes. Asegúrese de que la casilla esté marcada para 'Etiquetas en la primera fila' en la ventana del parámetro ANOVA.
4. Especifique alfa en la ventana de parámetros ANOVA. Alfa representa el nivel de significancia.
5. Genere los resultados en una nueva hoja de trabajo.

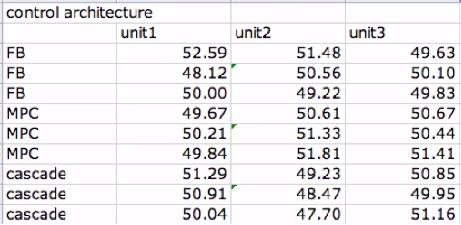
NOTA: Anova: Dos Factores con Replicación se utiliza en los casos en los que hay múltiples lecturas para un solo factor. Por ejemplo, la entrada a continuación, hay 2 factores, arquitectura de control y unidad. Esta entrada muestra cómo hay 3 lecturas correspondientes a cada arquitectura de control (FB, MPC y cascada). En este sentido, la arquitectura de control se replica 3 veces, cada vez proporcionando diferentes datos relativos a cada unidad. Entonces, en este caso, querría usar la opción Anova Two Factor with Replication.

Anova: Dos Factores sin Replicación se utiliza en los casos en los que solo hay una lectura perteneciente a un factor en particular. Por ejemplo, en el caso siguiente, cada muestra (fila) es independiente de las otras muestras ya que se basan en el día en que fueron tomadas. Dado que no se tomaron múltiples lecturas dentro del mismo día, se debe elegir la opción “sin replicación”.

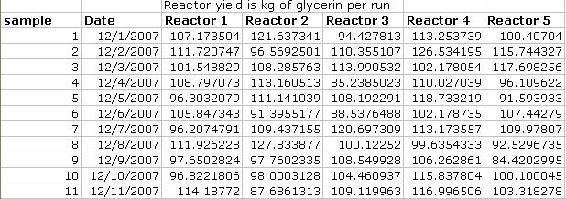
Salidas de Excel:

Resumen:
1. Conteo- número de puntos de datos en un conjunto
2. Suma- suma de los puntos de datos en un conjunto
3. Promedio- media de los puntos de datos en un conjunto
4. Varianza- desviación estándar de los puntos de datos en un conjunto

ANOVA:
1. Suma de cuadrados (SS)
2. El grado de libertad (df)
3. Los cuadrados medios (MS)
4. Estadístico F (F)
5. Valor P
6. F _crítico

Consulte la figura a continuación para ver un ejemplo de las entradas y salidas usando Anova: Single Factor. Anote la ubicación de la pestaña Análisis de datos. Los datos se obtuvieron de los programas de dieta descritos en el Cuadro 1. Dado que el estadístico F es mayor que F _crítico, la hipótesis nula puede ser rechazada a un nivel de confianza del 95% (ya que alfa se estableció en 0.05). Así, la pérdida de peso no fue aleatoria y de hecho depende del tipo de dieta elegida.

Ejemplo\(\PageIndex{1}\)

Determine la tasa de ensuciamiento del calderín con los siguientes parámetros:

• T = 410 K
• C _c = 16.7 g/L
• R _T = 145 min

¿Qué variable de proceso tiene el mayor efecto (por unidad) sobre la tasa de ensuciamiento del calderín?

Tenga en cuenta que las tablas a continuación son datos conformados. Los datos de salida para una sola entrada se recopilaron asumiendo que las otras variables de entrada proporcionan una salida insignificante. Si bien los factores que afectan el ensuciamiento del calderín son similares a los encontrados en el artículo vinculado en la sección “ANOVA y Análisis Factorial en Controles de Proceso”, los datos no lo son.

Temperatura del Reboiler (K)	400	450	500
Tasa de ensuciamiento (mg/min)	0.8	0.86	0.95

Concentración de catalizador (g/L)	10	20	30
Tasa de ensuciamiento (mg/min)	0.5	1.37	2.11

Tiempo de Residencia (min)	60	120	180
Tasa de ensuciamiento (mg/min)	0.95	2.3	3.81

Solución

1) Determinar el “factor de carga” para cada variable.

Esto se puede hacer usando cualquier herramienta de linealización. En este caso, el factor de carga es solo la pendiente de la línea para cada conjunto de datos. Usando Microsoft Excel, las ecuaciones para cada conjunto de datos son las siguientes:

Temperatura del Reboiler
y = 0.0015 * x + 0.195
Factor de carga: 0.0015 Concentración de

Catalizador
y = 0.0805 * x − 0.2833
Factor de carga: 0. 0805 Tiempo de

Residencia
y = 0.0238 * x − 0.5067
Factor de carga: 0.0238

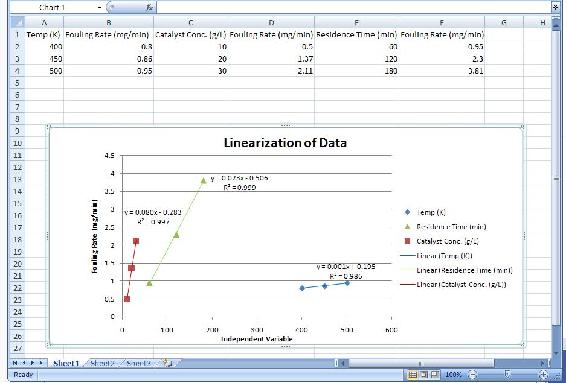
2) Determinar la tasa de ensuciamiento para las condiciones de proceso dadas y qué variable de proceso afecta más la tasa de ensuciamiento (por unidad). Tenga en cuenta que las unidades del valor de carga del factor son siempre las unidades de la salida divididas por las unidades de la entrada.

Conecte los valores de carga del factor en la siguiente ecuación:
Salida = f ₁ * entrada ₁ + f ₂ * entrada ₂ +... + f _n * entrada _n

Terminarás con:
FoulinGrate = 0.0015 * T + 0.0805 * C _c + 0.0238 * R _T

Ahora enchufa las variables de proceso:
FoulinGrate = 0.0015 * 410 + 0.0805 * 16.7 + 0.0238 * 145
FoulinGrate = 5.41 mg/min

La variable de proceso que más afecta a la tasa de ensuciamiento (por unidad) es la concentración de catalizador porque tiene la mayor valor de carga del factor.

Ejemplo\(\PageIndex{2}\)

El caudal de salida que sale de un tanque se está probando para 3 casos. El primer caso es bajo las condiciones normales de operación, mientras que el segundo (A) y el tercero (B) son para nuevas condiciones que se están probando. Se desea el valor de flujo de 7 (galones /hora) con un máximo de 10. Se prueban un total de 24 corridas con 8 corridas para cada caso. Las pruebas se realizan para determinar si alguna de las nuevas condiciones dará como resultado un caudal más preciso. Primero, determinamos si las nuevas condiciones A y B afectan el caudal. Los resultados son los siguientes:

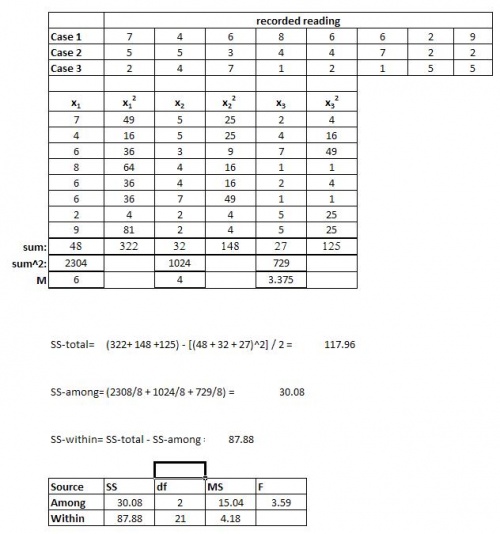
Se tabulan los valores registrados para los 3 casos. A continuación de esto se cuadran los valores para cada caso y se toman las sumas para todos estos. Para los 3 casos, las sumas son cuadradas y luego se encuentran sus medios.

Estos valores se utilizan para ayudar a determinar la tabla anterior (las ecuaciones dan una idea de cómo se calculan). De la misma manera con la ayuda de ANOVA, estos valores se pueden determinar más rápido. Esto se puede hacer usando la matematica explicada anteriormente.

Conclusión:

F _crítico equivale a 3.4668, de una tabla F. Dado que el valor F calculado es mayor que F _crítico, sabemos que existe una diferencia estadísticamente significativa entre 2 de las condiciones. Así, la hipótesis nula puede ser rechazada. Sin embargo no sabemos entre qué 2 condiciones hay diferencia. Un análisis post-hoc nos ayudará a determinarlo. Sin embargo estamos en condiciones de confirmar que hay una diferencia.

Ejemplo\(\PageIndex{3}\)

Como nuevo ingeniero in situ, una de sus tareas asignadas es instalar una nueva arquitectura de control para tres unidades diferentes. Se prueban tres unidades por triplicado, cada una con 3 arquitecturas de control diferentes: retroalimentación (FB), control predictivo de modelo (MPC) y control en cascada. En cada caso se mide el rendimiento y se organizan los datos de la siguiente manera:

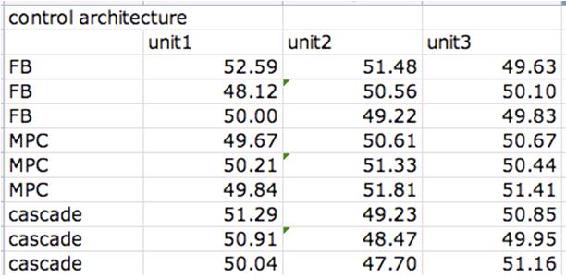
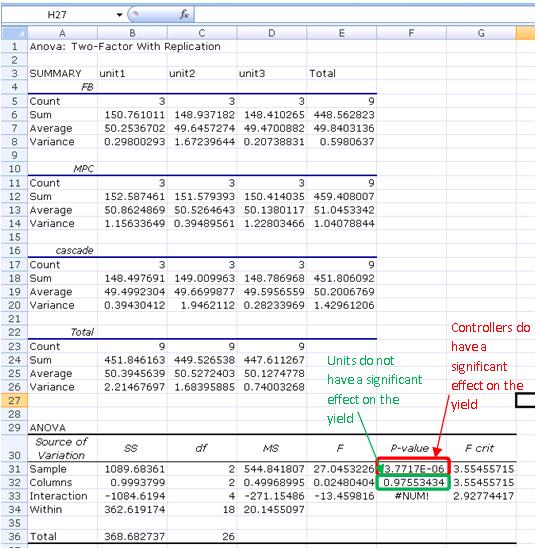
¿Las unidades difieren significativamente? ¿Las arquitecturas de control difieren significativamente?

Solución

Este problema se puede resolver usando ANOVA Dos factores con análisis de replicación.

Ejercicio\(\PageIndex{1}\)

El análisis ANOVA funciona mejor para?

1. Modelos no lineales
2. Modelos lineales
3. Modelos exponenciales
4. Todo lo anterior

Responder

B

Ejercicio\(\PageIndex{2}\)

¿Se utiliza el análisis ANOVA bidireccional para comparar?

1. Dos conjuntos de datos cualesquiera
2. Dos modelos ANOVA unidireccionales entre sí
3. Dos factores sobre su efecto de la salida
4. D. B y C

Responder

C

Referencias

• Ogunnaike, Babatunde y W. Harmon Ray. Dinámica de Procesos, Modelado y Control. Prensa de la Universidad de Oxford. Nueva York, NY: 1994.
• Uts, J. y R. Hekerd. Mente en Estadística. Capítulo 16 - Análisis de varianza. Belmont, CA: Brooks/Cole - Thomson Learning, Inc. 2004.
• Charles Spearman. Recuperado el 1 de noviembre de 2007, de www.indiana.edu/~intell/spearman.shtml
• Plonsky, M. “ANOVA unidireccional”. Recuperado el 13 de noviembre 2007, de www.uwsp.edu/psych/stat/12/anova-1w.htm
• Ender, Phil. “Cuadros Estadísticos F Distribución.” Recuperado el 13 de noviembre 2007, de www.gseis.ucla.edu/courses/help/dist3.html
• Devore, Jay L. Probabilidad y Estadística para la Ingeniería y las Ciencias. Capítulo 10 - El análisis de varianza. Belment, CA: Brooks/Cole - Thomson Learning, Inc. 2004.
• “Prueba mediana de Mood (Prueba de puntuaciones de signos)” Recuperado el 29 de noviembre de 2008, de www.micquality.com/six_sigma_glossary/mood_median_test.htm