13.10: Distribuciones Multinomiales

Última actualización
Guardar como PDF

Page ID: 85528

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

Los eventos estadísticos generan dos tipos de resultados: continuos o discretos. Los resultados continuos pueden tomar un número infinito de valores; por ejemplo, la altura de una persona puede tomar cualquier número real, por lo que hay infinitas posibilidades. Los eventos típicos que generan resultados continuos pueden seguir una distribución normal, exponencial o geométrica. Los resultados discretos solo pueden tomar valores prescritos; por ejemplo, una tirada de dados solo puede generar un número entero entre 1 y 6. Los resultados discretos suelen distribuirse binomialmente o multinomialmente. Es con la distribución multinomial que se refiere este artículo.

Distribuciones Multinomiales: Representación Matemática

Las distribuciones multinomiales tratan específicamente de eventos que tienen múltiples resultados discretos. La distribución binomial es un subconjunto específico de distribuciones multinomiales en las que solo hay dos posibles resultados de un evento.

Las distribuciones multinomiales no se limitan a eventos que solo tienen resultados discretos. Es posible categorizar los resultados con distribuciones continuas a diferentes grados (alto, medio, bajo). Por ejemplo, el nivel del agua -una entidad continua- en un tanque de almacenamiento puede hacerse discreto categorizándolos en “deseables” o “no deseables”. Las distribuciones multinomiales, por lo tanto, tienen aplicaciones expansivas en el control de procesos.

Función de densidad de probabilidad

Una forma de describir la probabilidad de que ocurra un resultado en un ensayo es la función de densidad de probabilidad. La función de densidad de probabilidad (PDF) representa matemáticamente la probabilidad de tener un resultado especificado. La función de densidad de probabilidad es una manera útil de encontrar la probabilidad de ocurrencia simultánea de resultados específicos (es decir$n_1 = 1$$n_2 = 1$, tener, y$n_3 = 1$ con 3 ensayos en oposición a otros resultados, como$n_1 = 3$,$n_2 = 0$,$n_3 = 0$ o$n_1 = 0$,$n_2 = 1$,$n_3 = 2$).

\[P\left(n_{1}, n_{2}, \ldots, n_{k}\right)=\left(n_{1} ! n_{2} ! \ldots n_{k} !\right) \prod_{i=1}^{N !} p_{i}^{n_{i}}=\left(n_{1} ! n_{2} ! \ldots n_{l \ell} !\right) *\left(p_{1}^{n_{1}} p_{2}^{n_{2}} \ldots p_{k}^{n_{k}}\right) \nonumber \]

donde

$N$es el número de ensayos
$k$es el número de posibles resultados
$n_i$es el número de ocurrencias de resultado$i$
$p_i$es la probabilidad de observar el resultado$i$

Sabemos que la suma de las probabilidades de todos los resultados posibles que puedan ocurrir en un juicio debe ser la unidad (ya que un resultado debe ocurrir). La función de densidad de probabilidad produce este resultado tanto para resultados continuos como discretos. Sin embargo, es importante señalar que para obtener este resultado para resultados continuos, se debe tomar la integral de la función de densidad de probabilidad sobre todos los resultados posibles. Para obtener este resultado de unidad para resultados discretos, se deben sumar las probabilidades de cada resultado (similar a tomar sumas de Riemann).

Función de distribución acumulativa

Mientras que la función de densidad de probabilidad calcula la probabilidad de un solo resultado, la función de distribución acumulativa (CDF) es una forma útil de encontrar la probabilidad de que un resultado se encuentre dentro de un rango dado de valores.

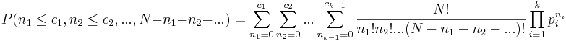
$(n_ {1}\ le c_ {1}, n_ {2}\ le c_ {2},... , n-n_ {1} -n_ {2} -...) =\ suma_ {n_ {1} =0} ^ {c_ {1}}\ suma_ {n_ {2} =0} ^ {c_ {2}}... \ sum_ {n_ {k-1} =0} ^ {c_ {k-1}}\ frac {N!} {n_ {1}! n_ {2}!... (N-n_ {1} -n_ {2} -...)!} \ prod_ {i=1} ^k p_i^ {n_i}$

donde

N es el número de ensayos
k es el número de posibles resultados
n _i es el número de ocurrencias del resultado i
p _i es la probabilidad de ver el resultado i
c _i es el número máximo de ocurrencias del resultado i

Visualización de la función de densidad de probabilidad con Mathematica

Antes de usar las funciones para distribuciones de probabilidad multinomial, se debe cargar un paquete especial usando el siguiente comando (dependiendo de la versión de Mathematica):

<< Necesidades ["MultivariatEstatistics`"] (Mathematica 6.0)

<< Estadísticas`MultidiscreteDistributions` (Mathematica 5.2)

Tenga en cuenta que el `(tilde) es la clave junto a 1 y no el carácter de comilla simple '.

Tabla de comandos pertinentes de Mathematica:

Comando	Descripción
PDF [multinomial, x]	función de densidad de probabilidad en x, donde x es escalar, vector o matriz según la distribución
CDF [multinomial, x]	función de distribución acumulativa en x
Media [multinomial]	media
Varianza [multinomial]	varianza
Desviación estándar [multinomial]	desviación estándar

Para trazar la función de densidad de probabilidad de distribución multinomial (PDF) en Mathematica, siga tres sencillos pasos:

Definición de la Distribución Multinomial

multinomial = multinomialDistribución [n, {p1, p2,... pk}] donde k es el número de resultados posibles, n es el número de resultados, y p1 a pk son las probabilidades de que ocurra ese resultado. n y p1 a pk generalmente se dan como números pero se pueden dar como símbolos siempre que se definan antes del comando.

Definición del PDF de la Distribución Multinomial

pdf=pdf [multinomial, {x1, x2,... , xk}]; La x aquí simplemente se refiere a la variable por lo que este comando se puede escribir tal cual, y dejar la x como una variable no un número.

Trazando el PDF

Plot3D [pdf, {x1, 0, 6}, {x2, 0, 5}, axesLabel -> {x1, x2, probabilidad}] los 0,6 y 0,5 son los rangos de x1 y x2 en la parcela respectivamente, y el argumento AxesLabel es para ayudarnos a ver cual es cual en la parcela creado. Este comando también se puede escribir tal cual, dejando todas las x como variables.

Tenga en cuenta que esto solo funcionará si tiene 2 variables. Si hay más variables, se pueden establecer restricciones para que se puedan trazar. Para 3 variables, establezca la tercera variable x3 como n-x1-x2. Consulte el cuaderno de Mathematica adjunto para obtener más información.

Medios:Multinomial.nb

Otras características

Históricamente, las estadísticas han sido útiles en el análisis descriptivo e inferencial de los datos. Asimismo, la distribución multinomial también es aplicable a las áreas mencionadas: estadística descriptiva, estadística inferencial y seissigma. En estas aplicaciones se utilizan varias variables clave:

El valor esperado a continuación describe la media de los datos. Las variables aleatorias discretas pueden tomar un rango de valores; la media de los datos describe la ubicación de los datos dentro de este rango.

\[\mathrm{E}\left(X_{i}\right)=n p_{i} \nonumber \]

La desviación estándar de los datos describe la varianza de los datos. La desviación estándar de los datos describe la dispersión de los datos con respecto al valor central (la media de los datos).

\[\operatorname{var}\left(X_{i}\right)=n p_{i}\left(1-p_{i}\right) \nonumber \]

Usando los parámetros anteriores, es posible encontrar la probabilidad de que los datos se encuentren dentro de n desviaciones estándar de la media. Al establecer n igual a 6, se puede implementar un control de calidad de seis sigma sobre el evento y los resultados en cuestión.

Derivación de la Distribución Binomial

Como se indicó anteriormente, la distribución binomial es simplemente un caso especial de la distribución multinomial. Usando la distribución multinomial, la probabilidad de obtener dos eventos n1 y n2 con probabilidades respectivas$p_1$ y$p_2$ a partir del$N$ total viene dada por:

\[P\left(n_{1}, n_{2}\right)=\frac{N !}{n_{1} ! n_{2} !}\left(p_{1}^{n_{1}} p_{2}^{n_{2}}\right) \nonumber \]

Si etiquetamos el evento de interés, digamos n1 en este caso, como “k”, entonces, ya que solo son posibles dos resultados, n2 debe ser igual a N-k. Por último, si etiquetamos la probabilidad de obtener k como simplemente “p”, entonces la probabilidad de obtener el evento n2 (p2) debe ser 1-p, porque nuevamente solo son posibles dos resultados. Con estas subsituciones, la ecuación anterior simplifica a

\[P(k, N, p)=\frac{N !}{k !(N-k) !} p^{k}(1-p)^{N-k} \nonumber \]

Cuál es la distribución binomial familiar, donde k es el número de eventos de interés, N es el número total de eventos y p es la probabilidad de alcanzar el evento de interés.

Aplicaciones de Distribuciones Multinomiales

Como se mencionó anteriormente, las distribuciones multinomiales son una versión generalizada de distribuciones binomiales. En aplicaciones de ingeniería química, las distribuciones multinomiales son relevantes para situaciones en las que hay más de dos posibles resultados (temperatura = {alta, med, baja}). Los sistemas multinomiales son una herramienta de análisis útil cuando una descripción de “éxito-fracaso” es insuficiente para entender el sistema. Una forma continua de la distribución multinomial es la distribución de Dirichlet.

El uso de la regla de Bayes es una de las principales aplicaciones de las distribuciones multinomiales. Por ejemplo, la Regla de Bayes se puede utilizar para predecir la presión de un sistema dada la temperatura y los datos estadísticos del sistema. La Regla de Bayes se puede utilizar para determinar la probabilidad de un evento o resultado como se mencionó anteriormente. Detalles adicionales sobre la Regla de Bayes se pueden encontrar en Regla de Bayes', probabilidad condicional, independencia.

Ejemplo de regla de Bayes

En caso de que hayas olvidado cómo usar la Regla de Bayes, aquí tienes un ejemplo que muestra cómo usarla para resolver un problema con un resultado multinomial que resulta de combinar posibilidades duales (como flujo deseado vs. flujo no deseado y configuración A vs configuración B).

Se le da un aparato de flujo con dos posibles configuraciones de válvula específicas, A y B. Para la configuración de válvula específica A, los caudales deseados se alcanzan 98.5% del tiempo. Y para la configuración específica de válvula B, los caudales deseados se logran 89.3% del tiempo. Un operador podría usar la configuración de A 79% del tiempo cuando se logran los caudales deseados. ¿Se puede determinar la probabilidad de que una configuración elegida aleatoriamente sea la misma que la de la configuración específica de válvula B y produzca caudales indeseables?

Solución resuelta

Vamos a utilizar los siguientes símbolos:

F _U: {caudales indeseables}
F _D: {caudales deseables}
C _B: {configuración del aparato B}

Así queremos encontrar: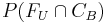 $(F_U\ cap C_B)$ , que es la probabilidad de caudales indeseables y configuración de válvula B.

Si usamos el Aparato A 79% del tiempo entonces la probabilidad de usar el Aparato B sería 21% o: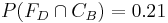 $(F_D\ cap C_B) =0.21$ , que es la probabilidad de usar la configuración B y obtener los caudales deseados.

Adicionalmente, se nos da: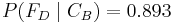 $(F_D\ mediados C_B) =0.893$ , que es la probabilidad de un caudal deseado, dado que se utiliza la configuración B.

Entonces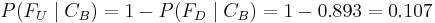 $(F_U\ mediados C_B) =1-P (F_D\ mediados C_B) =1-0.893=0.107$ , que es la probabilidad de que se obtenga un caudal indeseable, dado que se utiliza la configuración B.

A continuación se usa la información de arriba: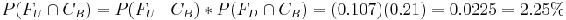 $(F_U\ cap C_B) =P (F_U\ mediados C_B) *P (F_D\ cap C_B) = (0.107) (0.21) =0.0225= 2.25%$ , que es la probabilidad de obtener un caudal indeseable y la configuración B que se encuentra tomando la probabilidad de obtener un caudal indeseable dado que se usa la configuración B y multiplicando eso por la probabilidad de un flujo deseable velocidad y configuración B.

Ejemplo$\PageIndex{1}$

Considera el escenario en el que arrojas un dado justo 12 veces. ¿Cuál es la probabilidad de que cada valor nominal (1-6) ocurra exactamente dos veces?

Solución

La probabilidad se puede determinar mediante una distribución multinomial en la que son posibles 6 resultados. Las probabilidades individuales son todas iguales dado que es un dado justo, p = 1/6. El número total de ensayos N es 12, y el número individual de ocurrencias en cada categoría n es 2.

\[P(2,2,2,2,2,2)-\frac{12 !}{2 ! 2 ! 2 ! 2 ! 2 ! 2 !} *\left(\frac{1}{6}\right)^{2}\left(\frac{1}{6}\right)^{2}\left(\frac{1}{6}\right)^{2}\left(\frac{1}{6}\right)^{2}\left(\frac{1}{6}\right)^{2}\left(\frac{1}{6}\right)^{2}-0.003488 \nonumber \]

Por lo tanto, la probabilidad de rodar exactamente 2 de cada valor nominal en un dado justo es de aproximadamente 0.35%.

Ejemplo$\PageIndex{2}$

Un cuenco tiene 2 canicas de maíz, 3 canicas azules y 5 canicas blancas. Se selecciona al azar una canica y luego se vuelve a colocar en el bol. Esto lo haces 5 veces. ¿Cuál es la probabilidad de elegir 1 mármol de maíz, 1 mármol azul y 3 canicas blancas?

Solución

N es el número de ensayos = 5
k es el número de resultados posibles = 3
n _i es el número de ocurrencias del resultado i
p _i es la probabilidad de ver el resultado i

Los tres posibles resultados son elegir un mármol de maíz, un mármol azul o un mármol blanco.

Debemos determinar n _i y p _i para resolver la distribución multinomial.

El número de ocurrencias del resultado es el número de veces que deseamos ver cada resultado. Estos se dan en la declaración del problema.

n _maíz = 1

n _azul = 1

n _blanco = 3

La probabilidad de ver cada resultado es fácil de encontrar. Por ejemplo, hay dos mármoles de maíz en el tazón de 10, por lo que la probabilidad de elegir un mármol de maíz es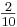 $textstyle\ frac {2} {10}$ .

p _maíz =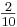 $textstyle\ frac {2} {10}$

p _azul =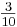 $textstyle\ frac {3} {10}$

p _blanco =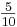 $textstyle\ frac {5} {10}$

Ahora podemos resolver la distribución multinomial como se muestra a continuación. La probabilidad de elegir 1 mármol de maíz, 1 mármol azul y 3 mármoles blancos es de 0.15.

\[P(1,1,3)=\frac{5 !}{1 ! 1 ! 3 !} *\left(\frac{2}{10}\right)^{1}\left(\frac{3}{10}\right)^{1}\left(\frac{5}{10}\right)^{3}=0.15 \nonumber \]

Ejemplo$\PageIndex{3}$

Se utilizan dos válvulas para controlar el flujo de líquido que sale de un tanque de almacenamiento (Tanque 1) hacia otro tanque de almacenamiento (Tanque 2) y se controlan mediante las Válvulas 1 y 2 como se ve a continuación. Las válvulas existen en dos estados: abierto y cerrado.

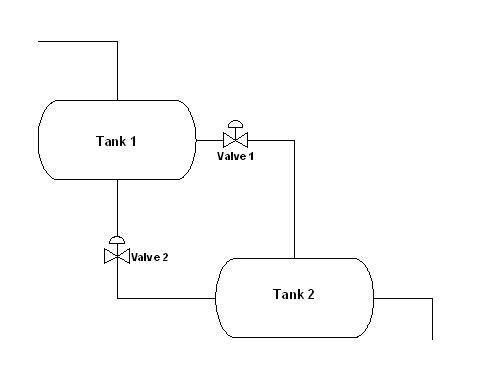
ultinomial diagram.JPG

La siguiente tabla describe las cuatro configuraciones de válvula diferentes y la frecuencia del flujo deseado para cada configuración de válvula en base a datos experimentales.

Configuración	Válvula 1	Válvula 2	Probabilidad de que esa configuración tenga el mejor flujo
1	Abierto	Cerrado	0.305
2	Abierto	Abierto	0.476
3	Cerrado	Abierto	0.218
4	Cerrado	Cerrado	0.001

Para reducir costos, se están considerando dos aparatos diferentes con una configuración similar, pero con diferentes dimensiones de tubería para reemplazar el aparato original. A continuación se presentan tablas de datos para cada aparato de reemplazo potencial con diferentes configuraciones de válvula y el número de veces de cada 100 mediciones que la configuración de la válvula dio el flujo deseado.

Aparato 1

Configuración	Válvula 1	Válvula 2	# de Mejor Flujo
1	Abierto	Cerrado	42
2	Abierto	Abierto	37
3	Cerrado	Abierto	21
4	Cerrado	Cerrado	0

Aparato 2

Configuración	Válvula 1	Válvula 2	# de Mejor Flujo
1	Abierto	Cerrado	20
2	Abierto	Abierto	22
3	Cerrado	Abierto	56
4	Cerrado	Cerrado	2

Con base en la información anterior, ¿qué aparato se parece más al modelo deseado? ¿Por cuánto?

Solución

Con las 4 configuraciones de válvulas diferentes, se puede utilizar la distribución multinomial para calcular la probabilidad de una medición. El objetivo aquí es encontrar el modelo con la función de densidad de probabilidad más alta, porque ese es más como el modelo deseado.

La probabilidad de una medición se puede calcular de la siguiente manera dado que existen 4 configuraciones diferentes de válvulas posibles (ver sección en pdf para obtener más información sobre de dónde proviene esta ecuación):

\[P\left(n_{1}, n_{2}, n_{3}, n_{4}\right)=\frac{N !}{n_{1} ! n_{2} ! n_{3} ! n_{4} !} p_{1}^{n_{1}} p_{2}^{n 2} p_{3}^{n 3} p_{4}^{n 4} \nonumber \]

donde

n _i = número total de mediciones con el mejor caudal de cada configuración de válvula
i = configuración
p _i = probabilidad de que esa configuración tenga el mejor flujo
N = Número total de observaciones

El cálculo de la probabilidad de cada aparato se puede hacer de manera similar:

Aparato 1:

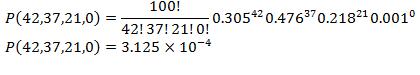
Aparato 2:
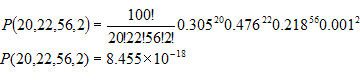
ultinomial ex1 App2Prob.jpg

Basado en los cálculos anteriores para ambos aparatos, el Aparato 1 se parece más al modelo deseado. El aparato 1 tiene una función de densidad de probabilidad más alta, basada en la probabilidad relativa de cada flujo de configuración.

Esta figura muestra el código de Mathematica que puede ser utilizado para resolver la probabilidad de una distribución multinomial. Los n valores son el número de ocurrencias de cada resultado y los valores p son las probabilidades de cada salida. La función se establece para una distribución multinomial con cinco resultados diferentes. Sin embargo, se puede utilizar para distribuciones multinomiales con menos resultados estableciendo los valores n no utilizados en 0 y los valores de p no utilizados en cualquier número que no sea 0. Esta figura también muestra las probabilidades calculadas a partir del Aparato 1 y el Aparato 2.

Ejemplo$\PageIndex{4}$

Una reacción fuera de control ocurre cuando la generación de calor a partir de una reacción exotérmica excede la pérdida de calor. La temperatura elevada aumenta la velocidad de reacción, aumentando aún más la generación de calor y la acumulación de presión dentro del reactor. En conjunto, la escalada incontrolada de temperatura y presión dentro de un reactor puede provocar una explosión.

Los precursores de una reacción fuera de control - alta temperatura y presión - se pueden detectar mediante la instalación de sensores confiables de temperatura y presión dentro del reactor. Las reacciones fuera de control pueden prevenirse bajando la temperatura y/o presión dentro del reactor antes de que alcancen niveles peligrosos. Esta tarea se puede lograr enviando una corriente inerte fría al reactor o ventilando el reactor.

Les Lloyd es ingeniero de procesos en Miles Reactor Company que ha sido asignado para trabajar en un nuevo proceso de reacción. Utilizando datos históricos de todas las reacciones similares que se han realizado antes, Les ha estimado las probabilidades de que cada resultado ocurra durante el nuevo proceso. Los posibles resultados del proceso incluyen todas las permutaciones de las posibles temperaturas de reacción (bajas y altas) y presiones (bajas y altas). Ha combinado esta información en la siguiente tabla:

Resultado	Temperatura	Presión	Probabilidad
1	alto	alto	0.013
2	alto	bajo	0.267
3	bajo	alto	0.031
4	bajo	bajo	0.689

Preocupada por el riesgo de reacciones desbocadas, Miles Reactor Company está implementando un nuevo programa para evaluar la seguridad de sus procesos de reacción. El programa consiste en ejecutar cada proceso de reacción 100 veces durante el próximo año y registrar las condiciones del reactor durante el proceso cada vez. Para que el proceso se considere seguro, los resultados del proceso deben estar dentro de los siguientes límites:

Resultado	Temperatura	Presión	Frecuencia
1	alto	alto	n ₁ = 0
2	alto	bajo	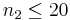$n_ {2}\ le 20$
3	bajo	alto	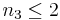$n_ {3}\ le 2$
4	bajo	bajo	n ₄ = 100 − n ₁ − n ₂ − n ₃

Ayudar a Les a predecir si el nuevo proceso es seguro o no respondiendo a la siguiente pregunta: ¿Cuál es la probabilidad de que el nuevo proceso cumpla con las especificaciones del nuevo programa de seguridad?

Solución

La probabilidad de que se cumplan las pautas de seguridad viene dada por la siguiente expresión de CDF:

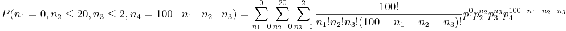
$(n_ {1} = 0, n_ {2}\ le 20, n_ {3}\ le 2, n_ {4} = 100-n_ {1} -n_ {2} -n_ {3}) =\ suma_ {n_ {1} =0} ^ {0}\ suma_ {n_ {2} =0} ^ {20}\ sum_ {n_ {3} =0} ^ {2}\ frac {100!} {n_ {1}! n_ {2}! n_ {3}! (100-n_ {1} -n_ {2} -n_ {3})!} p_1^0 p_2^ {n_2} p_3^ {n_3} p_4^ {100-n_1-n_2-n_3}$

donde

N es el número de ensayos
k es el número de posibles resultados
n _i es el número de ocurrencia del resultado i
p _i es la probabilidad de ver el resultado i
c _i es el número máximo de ocurrencia del resultado i

Esta expresión CDF se puede evaluar usando los siguientes comandos en Mathematica:

<< Necesidades ["MultivariatEstatistica`"]
<< multinomial = Distribución multinomial [100, {0.013, 0.267, 0.031, 0.689}]
<< CDF [multinomial, {0, 20, 2, 78}]

El resultado es:

\[P\left(n_{-}=0, n_{2} \leq 20, n_{3} \leq 2, n_{4}=1000-n_{1}-n_{2}-n_{3}\right)=0.00132705 \nonumber \]

Con base en este cálculo de probabilidad, parece poco probable que este nuevo proceso pase las nuevas pautas de seguridad.

Rincón de Sage

www.youtube.com/v/aalqprehy5c
Para diapositivas de esta presentación por el Grupo Si: Media:Multinomial Distribution.ppt

Referencias

Woolf, Peter, Amy Keating, Christopher Burge, y Michael Yaffe. (2004). Estadística e Imprimación de Probabilidad para Biólogos Computacionales. Instituto Tecnológico de Massachusetts.
“Distribución Multinomial”. Wikipedia. es.wikipedia.org/wiki/Distribución_Multinomial_.
Perry, R.H. (1997). Manual del ingeniero químico de Perry, 7a edición, McGraw-Hill. ISBN 978-0-07-049841-9
Calculadora Multinomial: Calculadora Estadística en Línea. Accedido 27 nov. 2007. http://stattrek.com/Tables/multinomial.aspx#calculator

Colaboradores

Autores: Hillary Kast, Andrew Kim, Adhi Paisoseputra, Stephanie Van Kirk
Mayordomos: Gillian Berberich, Katie Feldt, Christopher Mark, Jason Wong

Search

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)