14.2: Diseño de experimentos a través de diseños factoriales
- Page ID
- 85549
El diseño factorial es un método importante para determinar los efectos de múltiples variables en una respuesta. Tradicionalmente, los experimentos están diseñados para determinar el efecto de UNA variable sobre UNA respuesta. R.A. Fisher demostró que existen ventajas al combinar el estudio de múltiples variables en un mismo experimento factorial. El diseño factorial puede reducir el número de experimentos que uno tiene que realizar al estudiar múltiples factores simultáneamente. Adicionalmente, se puede utilizar para encontrar tanto los efectos principales (de cada factor independiente) como los efectos de interacción (cuando ambos factores deben ser utilizados para explicar el resultado). Sin embargo, el diseño factorial solo puede dar valores relativos, y para lograr valores numéricos reales la matemática se vuelve difícil, ya que es necesario realizar regresiones (que requieren minimizar una suma de valores). Independientemente, el diseño factorial es un método útil para diseñar experimentos tanto en entornos de laboratorio como industriales.
El diseño factorial prueba todas las condiciones posibles. Debido a que el diseño factorial puede conducir a un gran número de ensayos, que pueden llegar a ser costosos y consumir mucho tiempo, el diseño factorial se usa mejor para un pequeño número de variables con pocos estados (1 a 3). El diseño factorial funciona bien cuando las interacciones entre variables son fuertes e importantes y donde cada variable contribuye significativamente.
¿Qué es el diseño factorial?
Ejemplo de diseño factorial
La forma más fácil de entender cómo funciona el diseño factorial es leer un ejemplo. Supongamos que a usted, un científico que trabaja para la FDA, le gustaría estudiar y medir la probabilidad de que los pacientes sufran convulsiones después de tomar un nuevo medicamento farmacéutico llamado CureAll. CureAll es una droga novedosa en el mercado y puede curar casi cualquier dolencia del cuerpo. Usted junto con sus compañeros de trabajo en la FDA han decidido probar dos niveles de dosificación: 5 mg y 10 mg. También te interesa determinar si los efectos secundarios del medicamento difieren entre los adultos más jóvenes (20 años) y los adultos mayores (40 años). Con base en la información dada, se ve que existen dos factores: la dosis y la edad. Los factores son las principales categorías a explorar a la hora de determinar la causa de las convulsiones en los pacientes. Bajo cada uno de estos factores, existen diferentes niveles: 5 y 10 mg para la dosis; 20 y 40 años para la edad. Un nivel es básicamente una de las subdivisiones que conforman un factor. A partir de esta información, podemos ver que tenemos un diseño factorial de 2 x 2, lo que significa que tendremos 2 * 2 = 4 grupos. Un grupo es conjunto de condiciones que conformarán ese experimento en particular.
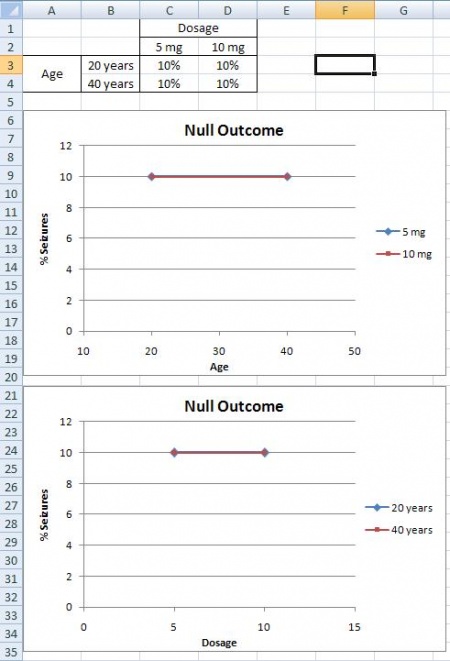
Resultado nulo
Una situación de resultado nulo es cuando el resultado de tu experimento es el mismo independientemente de cómo se combinaron los niveles dentro de tu experimento. Del ejemplo anterior, existiría un desenlace nulo si recibieras el mismo porcentaje de convulsiones que ocurren en pacientes con dosis y edad variables. Los gráficos a continuación no ilustran ningún cambio en el porcentaje de convulsiones para todos los factores, por lo que se puede concluir que la posibilidad de padecer una convulsión no se ve afectada por la dosis del medicamento o la edad del paciente.
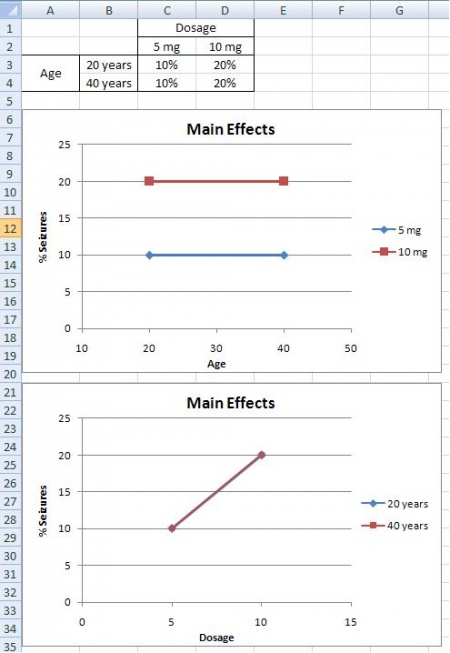
Efectos principales
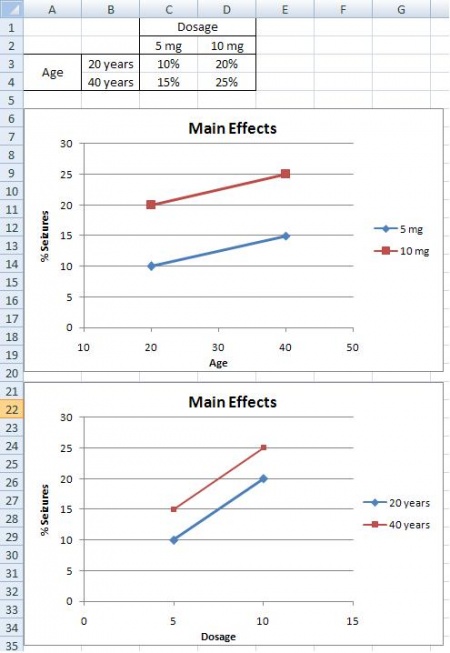
Una situación de efectos principales es cuando existe una tendencia consistente entre los diferentes niveles de un factor. Del ejemplo anterior, supongamos que encuentra que a medida que aumenta la dosis, también aumenta el porcentaje de personas que sufren convulsiones. También notas que la edad no juega un papel; tanto los de 20 como los 40 años sufren el mismo porcentaje de convulsiones por una cantidad determinada de CureAll. A partir de esta información, se puede concluir que la posibilidad de que un paciente sufra una convulsión se minimiza a dosis más bajas del medicamento (5 mg). La segunda gráfica ilustra que con el aumento de la dosis del medicamento hay un mayor porcentaje de convulsiones, mientras que la primera gráfica ilustra que con el aumento de la edad no hay cambio en el porcentaje de convulsiones. Ambas gráficas sólo contienen un efecto principal, ya que sólo la dosis tiene un efecto el porcentaje de convulsiones. Mientras que las gráficas tres y cuatro tienen dos efectos principales, ya que la dosis y la edad tienen un efecto sobre el porcentaje de convulsiones.
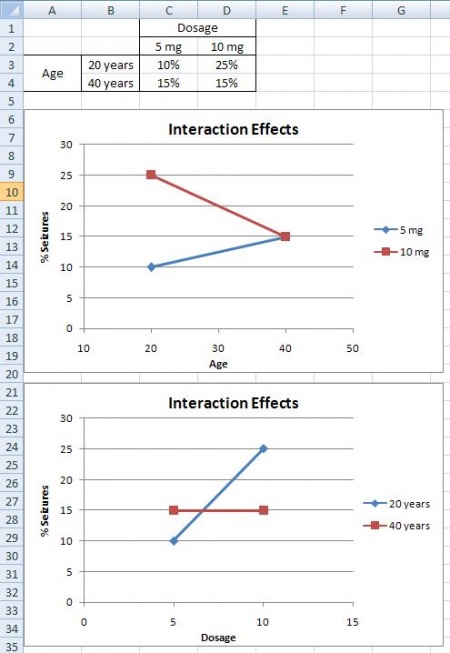
Efectos de interacción
La situación de los efectos de interacción es el último resultado que se puede detectar mediante el diseño factorial. Del ejemplo anterior, suponga que encuentra que los niños de 20 años sufrirán convulsiones el 10% de las veces cuando se les administra una píldora CureAll de 5 mg, mientras que los de 20 años sufrirán el 25% de las veces cuando se les administra una píldora CureAll de 10 mg. Sin embargo, cuando a los niños de 40 años se les administra una pastilla de 5 mg o una píldora de 10 mg, el 15% sufre convulsiones en ambas dosis. Esta correlación se puede ver en las gráficas a continuación. Hay una probabilidad cada vez mayor de padecer una convulsión a dosis más altas para los niños de 20 años, pero no hay diferencia en padecer convulsiones para los niños de 40 años. Por lo tanto, debe haber un efecto de interacción entre la dosis de CureAll, y la edad del paciente que toma el medicamento. Cuando tienes un efecto de interacción es imposible describir tus resultados con precisión sin mencionar ambos factores. Siempre se puede detectar una interacción en las gráficas porque cuando hay líneas que no son paralelas hay una interacción presente. Si observas los gráficos de efectos principales anteriores, notarás que todas las líneas dentro de una gráfica son paralelas. En contraste, para las gráficas de efectos de interacción, verás que las líneas no son paralelas.
Enfoque de Análisis Matemático
En la sección anterior, se analizó un enfoque cualitativo para determinar los efectos de diferentes factores utilizando el diseño factorial. Ahora vamos a cambiar de marcha y mirar el diseño factorial en un enfoque cuantitativo para determinar cuánta influencia tienen los factores en un experimento en el resultado.
Cómo lidiar con un diseño factorial de 2 n
Supongamos que tiene dos variables\(A\)\(B\) y y cada una tiene dos niveles a 1, a 2 y b 1, b 2. Mediría los efectos de combinación de\(A\) y\(B\) (a 1 b 1, a 1 b 2, a 2 b 1, a 2 b 2). Ya que tenemos dos factores, cada uno de los cuales tiene dos niveles, decimos que tenemos un diseño factorial de 2 x 2 o 2 2. Por lo general, al realizar el diseño factorial, habrá dos niveles, y n factores diferentes. Así, la forma general del diseño factorial es de 2 n.
Para encontrar el efecto principal de\(A\), utilizamos la siguiente ecuación:
\[A = (a_2b_1 - a_1b_1) + (a_2b_2 - a_1b_2) \nonumber \]
Del mismo modo, el efecto principal de B viene dado por:
\[B = (b_2a_1 - b_1a_1) + (b_2a_2 - b_1a_2) \nonumber \]
Por la experimentación tradicional, cada experimento tendría que aislarse por separado para encontrar completamente el efecto en B. Esto habría resultado en la realización de 8 experimentos diferentes. Tenga en cuenta que solo se requirieron cuatro experimentos en diseños factoriales para resolver los ocho valores en A y B. Esto muestra cómo el diseño factorial es un ahorro de tiempo.
Al tomar los coeficientes en A y B, se creó la siguiente tabla.
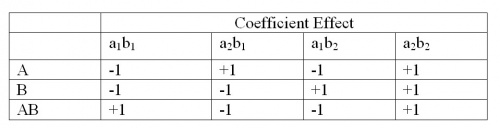
AB se encuentra multiplicando los coeficientes de a x b x para obtener el nuevo efecto de coeficiente.
La complicación adicional es el hecho de que se requiere más de un prueba/replicación para la precisión, por lo que esto requiere sumar cada subefecto (por ejemplo, sumar los tres ensayos de un 1 b 1). Al sumar los efectos de coeficiente con los subefectos (multiplicar coeficiente con subefecto), se puede encontrar un efecto factorial total. Este valor determinará si el factor tiene un efecto significativo en el resultado. Para números mayores, el factor puede considerarse extremadamente importante y para números más pequeños, el factor puede considerarse menos importante. El signo del número también tiene una correlación directa con que el efecto sea positivo o negativo.
Para obtener un efecto factorial medio, los totales deben dividirse por 2 veces el número de réplicas, donde una réplica es un experimento repetido.
\[\text {mean factorial effect} = \dfrac{\text{total factorial effect}}{2r} \nonumber \]
Al sumar una tercera variable (\(C\)), el proceso de obtención de los coeficientes se complica significativamente. El principal efecto factorial para\(A\):
\[A=\left(a_{2} b_{1} c_{1}-a_{1} b_{1} c_{1}\right)+\left(a_{2} b_{2} c_{1}-a_{1} b_{2} c_{1}\right)+\left(a_{2} b_{1} c_{2}-a_{1} b_{1} c_{2}\right)+\left(a_{2} b_{2} c_{2}-a_{1} b_{2} c_{2}\right) \nonumber \]
La tabla de coeficientes se enumera a continuación
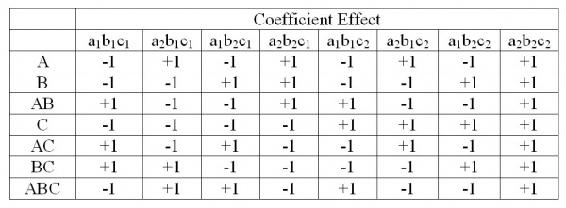
Es claro que para encontrar los efectos factoriales totales, habría que encontrar los efectos principales de la variable y luego los coeficientes. El algoritmo Yates se puede utilizar para simplificar el proceso.
Algoritmo
Frank Yates creó un algoritmo para encontrar fácilmente los efectos factoriales totales en un factorial de 2 n que es fácilmente programable en Excel. Si bien este algoritmo es bastante sencillo, también es bastante tedioso y se limita a 2 n diseños factoriales. Así, la tecnología moderna ha permitido que este análisis se realice utilizando programas de software estadístico a través de regresión.
Pasos:
- En la primera columna, enumere todas las combinaciones experimentales individuales
De acuerdo con el orden de Yates, tal como sigue para un diseño factorial 2 3
- - -
+ - -
- + -
+ + -
- - +
+ - +
- + +
+ + +
- En la segunda columna, enumere todos los totales de cada combinación
- Las primeras cuatro entradas de la tercera columna (Etapa 1) se obtienen sumando pares de la “lista de totales” (columna anterior). Los siguientes cuatro números se obtienen restando el número superior del número inferior de cada par.
- La cuarta columna (Etapa 2) se obtiene de la misma manera, pero esta vez sumando y restando pares de la Etapa 1.
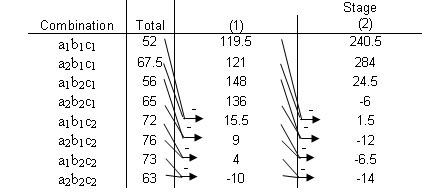
- La quinta columna (Etapa 3) se obtiene de la misma manera, pero esta vez sumando y restando pares de la Etapa 2.
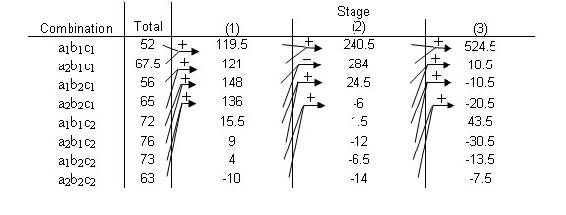
- Continuar con Etapas hasta llegar a n, o el número de factores. Esta columna final es el Efecto Total. Un valor positivo significa una correlación positiva y un valor negativo significa una correlación negativa. Estos valores son todos relativos, sin embargo, por lo que no hay forma de comparar diferentes totales de efectos de diferentes experimentos.
Ignorando la primera fila, busque en la última etapa y encuentre la variable que tenga el mayor número relativo, entonces esa fila indica el EFECTO TOTAL PRINCIPAL. El Efecto Total Principal se puede relacionar con las variables de entrada moviéndose a lo largo de la fila y mirando la primera columna. Si la fila en la primera columna es a 2 b 1 c 1 entonces el efecto total principal es A. La fila para un 1 b 2 c 1 sería para B. La fila para un 2 b 1 c 2 sería para AC.
Este valor de efecto total principal para cada variable o combinación de variables será algún valor que signifique la relación entre la salida y la variable. Por ejemplo, si tu valor es positivo, entonces hay una relación positiva entre la variable y la salida (es decir, a medida que aumentas la variable, la salida también aumenta). Un valor negativo significaría una relación negativa. Observe, sin embargo, que los valores son todos relativos entre sí. Entonces, si bien el mayor valor de efecto total principal en un conjunto de experimentos puede tener un valor de 128, otro experimento puede tener su mayor valor de efecto total principal sea 43. No hay forma de determinar si un valor de 128 en un experimento tiene más control sobre su salida que un valor de 43, pero a los efectos de comparar variables dentro de un experimento, el efecto total principal sí permite ver el control relativo que tienen las variables en la salida.
Ejemplo de diseño factorial revisitado
Recordemos el ejemplo dado en la sección anterior ¿Qué es el Diseño Factorial? En el ejemplo, hubo dos factores y dos niveles, lo que dio un diseño factorial 2 2. El Algoritmo de Yates se puede utilizar para determinar cuantitativamente qué factor afecta más el porcentaje de convulsiones. Para el uso del algoritmo de Yates, llamaremos factor de edad A con un 1 = 20 años, y un 2 = 40 años. De igual manera, llamaremos factor de dosis B, con b 1 = 5 mg, y b 2 = 10 mg. Los datos para los tres resultados se toman de las cifras dadas en el ejemplo, asumiendo que los datos dados resultaron de múltiples ensayos.
Resultado nulo
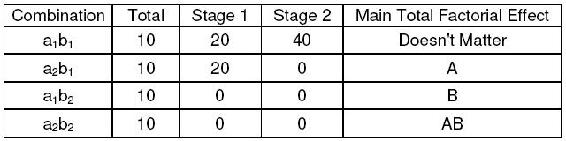
Se construyó la siguiente tabla de algoritmos de Yates utilizando los datos para el resultado nulo. Como se ve en la tabla, los valores del efecto factorial total principal son 0 para A, B y AB. Esto demuestra que ni la dosis ni la edad tienen ningún efecto sobre el porcentaje de convulsiones.
Efecto Principal
Se construyó la siguiente tabla de algoritmos de Yates utilizando los datos de las dos primeras gráficas de la sección de efectos principales. Además de la primera fila de la tabla, la fila con el mayor efecto factorial total principal es la fila B, mientras que el efecto total principal para A es 0. Esto significa que la dosis (factor B) afecta el porcentaje de convulsiones, mientras que la edad (factor A) no tiene ningún efecto, que también es lo que se vio gráficamente.
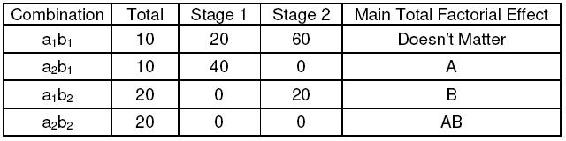
Se construyó la siguiente tabla de algoritmos de Yates utilizando los datos de las dos segundas gráficas de la sección de efectos principales. Además de la primera fila de la tabla, el valor principal del efecto total fue 10 para el factor A y 20 para el factor B. Esto significa que tanto la edad como la dosis afectan el porcentaje de convulsiones. Sin embargo, dado que el valor para B es mayor, la dosis tiene un mayor efecto sobre el porcentaje de convulsiones que la edad. Esto es lo que se vio gráficamente, ya que la gráfica con dosis en el eje horizontal tiene una pendiente con mayor magnitud que la gráfica con la edad en el eje horizontal.
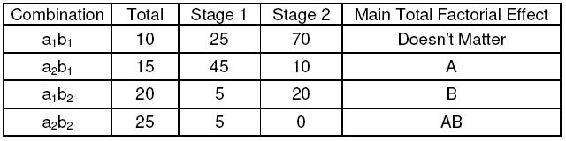
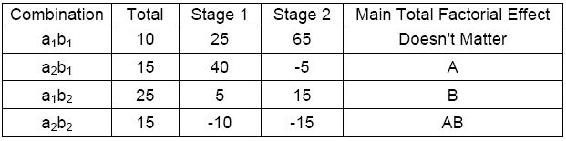
Efecto de interacción
La siguiente tabla de algoritmos de Yates se construyó utilizando los datos de la sección de efectos de interacción. Dado que el principal efecto factorial total para AB es distinto de cero, existen efectos de interacción. Esto significa que es imposible correlacionar los resultados con uno u otro factor; ambos factores deben ser tomados en cuenta.
Aplicaciones de ingeniería química
Debe quedar bastante claro que el diseño factorial se puede integrar fácilmente en una aplicación de ingeniería química. Muchos ingenieros químicos enfrentan problemas en sus trabajos cuando se ocupan de cómo determinar los efectos de diversos factores en sus resultados. Por ejemplo, supongamos que tienes un reactor y quieres estudiar el efecto de la temperatura, concentración y presión en múltiples salidas. Para minimizar el número de experimentos que tendrías que realizar, puedes utilizar el diseño factorial. Esto le permitirá determinar los efectos de la temperatura y la presión mientras se ahorra dinero en la realización de experimentos innecesarios.
Un estudio de 2007 sobre la conversión de paja de trigo en combustible utilizó un diseño factorial para estudiar el efecto de cuatro factores en la composición y susceptibilidad a la hidrólisis enzimática del producto final. (Pérez, et.al.). La siguiente tabla muestra el diseño factorial completo para el estudio. Los cuatro factores que se estudiaron tuvieron solo dos niveles y trataron parámetros de pretratamiento. Fueron: Temperatura del agua, tiempo de residencia, fracción sólida y sobrepresión en el reactor. No es necesario entender en qué consiste cada uno de estos para entender el diseño experimental. Como se ve en la siguiente tabla, hubo dieciséis ensayos, o 2^4 experimentos.
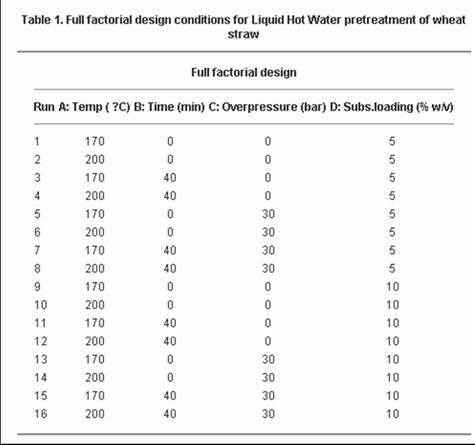
Fuente: Pérez, et. al.
Ejemplo de DOE de Minitab
Minitab 15 Statistical Software es un poderoso programa de estadísticas capaz de realizar regresiones, ANOVA, gráficos de control, DOE y mucho más. Minitab es especialmente útil para crear y analizar los resultados de los estudios del DOE. Es posible crear DOEs factorial, superficie de respuesta, mezcla y método taguchi en Minitab. A continuación se analiza el método general para crear DOE factoriales.
Creación de DOE factorial
Minitab proporciona un método simple y fácil de usar para diseñar una tabla de experimentos. Adicionalmente, el análisis de múltiples respuestas (resultados obtenidos de la experimentación) para determinar qué parámetros afectan significativamente las respuestas es fácil de hacer con Minitab. El software estadístico Minitab 15 se puede utilizar a través de Laboratorios CAEN virtuales yendo a Inicio>Todos los programas>Métodos matemáticos y numéricos>Soluciones Minitab>Software estadístico Minitab 15.
El primer paso es crear el DOE especificando el número de niveles (típicamente 2) y el número de respuestas. Para ello, ve a STAT>DOE>Factorial>Crear Diseño Factorial como se muestra en la imagen de abajo.
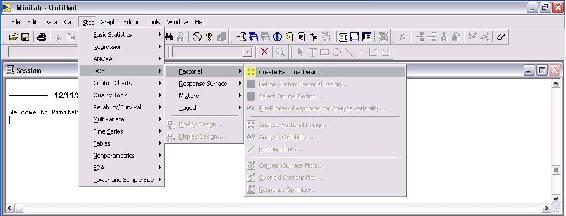
La siguiente imagen es el menú de opciones “Crear diseño factorial”.
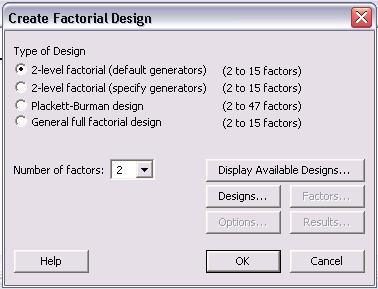
Para un diseño de 2 niveles, haga clic en el botón de opción “Factorial de 2 niveles (generadores predeterminados)”. A continuación, especifique el número de factores entre 2 y 15. Se pueden elegir otros diseños como Plackett-Burman o un diseño factorial completo General. Para obtener información sobre estos diseños, consulte el menú “Ayuda”.
Después de elegir el número de factores, haga clic en la opción “Diseños...” para ver el siguiente menú.
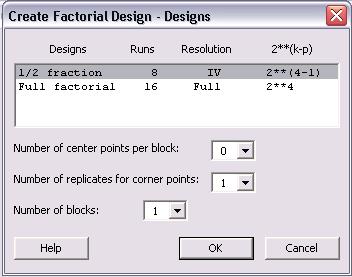
En este menú, se puede elegir una fracción 1/2 o un diseño factorial completo. Aunque el factorial completo proporciona una mejor resolución y es un análisis más completo, la fracción 1/2 requiere la mitad del número de corridas que el diseño factorial completo. A falta de tiempo o para hacerse una idea general de las relaciones, el diseño de 1/2 fracción es una buena opción. Adicionalmente, en este menú se puede elegir el número de puntos centrales por bloque, el número de réplicas para los puntos de esquina y el número de bloques. Consulte el menú “Ayuda” para obtener detalles sobre estas opciones. Haga clic en “Ok” una vez que se haya elegido el tipo de diseño.
Una vez elegido el diseño, los “Factores... Los botones “, “Opciones...” y “Resultados...” se vuelven activos en el menú de opciones “Crear diseños factoriales”. Haga clic en el botón “Factores...” para ver el siguiente menú.
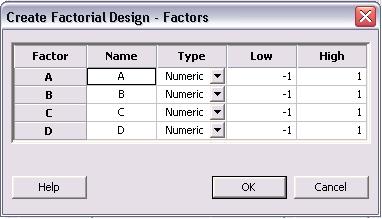
La imagen de arriba es para un diseño de 4 factores. Los factores A - D pueden renombrarse para representar los factores reales del sistema. Los factores pueden ser numéricos o de texto. Adicionalmente, un valor bajo y alto se listan inicialmente como -1 y 1, donde -1 es el valor bajo y 1 es el valor alto. Los niveles bajo y alto para cada factor se pueden cambiar a sus valores reales en este menú. Haga clic en “Aceptar” una vez que se complete esto.
Los pasos necesarios para crear el DOE están completos, pero se pueden especificar otras opciones para “Resultados...” y “Opciones...”. A continuación se muestran los menús de “Resultados...” y “Opciones...”.
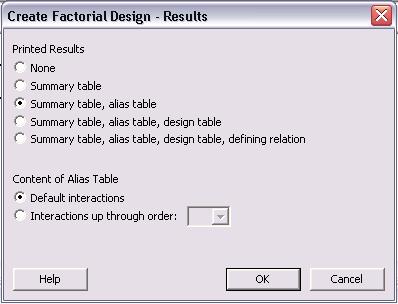
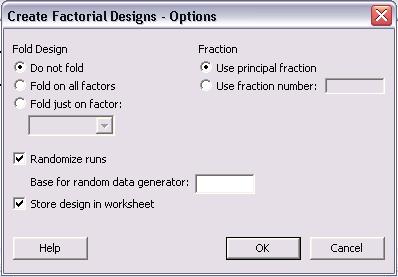
En el menú principal “Crear diseño factorial”, haga clic en “Aceptar” una vez que se hayan completado todas las especificaciones. Se obtiene la siguiente tabla para un diseño factorial completo de 2 niveles, 4 factores. Ninguno de los niveles se especificó ya que aparecen como -1 y 1 para niveles bajos y altos, respectivamente.
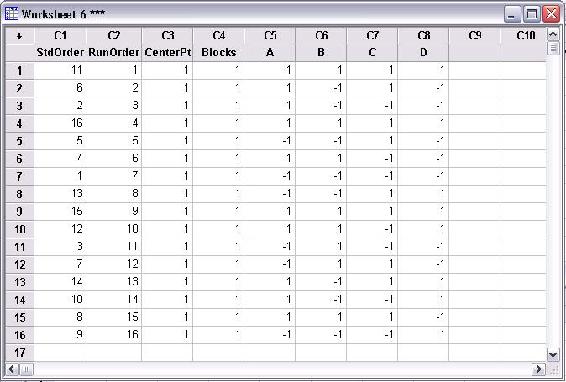
El cuadro anterior contiene todas las condiciones requeridas para un DOE factorial completo. Minitab muestra el orden estándar y el orden de ejecución aleatoria en las columnas C1 y C2, respectivamente. Las columnas A-D son los factores. La primera ejecución (según lo especificado por el orden de ejecución aleatoria) debe realizarse en los niveles bajos de A y C y los niveles altos de B y D. Se requiere un total de 16 corridas para completar el DOE.
Modificación de la tabla DOE
Una vez que se ha creado una tabla de ensayos para el DOE, se pueden realizar modificaciones adicionales según sea necesario. Algunas modificaciones típicas incluyen modificar el nombre de cada factor, especificar el nivel alto y bajo de cada factor, y agregar réplicas al diseño. Al ser modificaciones de un diseño actual, vaya a STAT>DOE>Modify Design... como se ve en la siguiente figura.
Se muestra el siguiente menú para modificar el diseño.
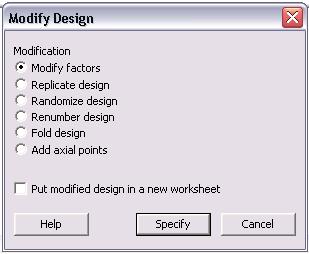
En el menú “Modificar diseño”, los usuarios pueden modificar factores, replicar el diseño, aleatorizar el diseño, renumerar el diseño, plegar el diseño y agregar puntos axiales. Adicionalmente, cualquier cambio realizado se puede poner en una nueva hoja de trabajo. Para cambiar los factores, haga clic en el botón de opción “Modificar factores” y luego en “Especificar” para ver el siguiente menú de opciones.
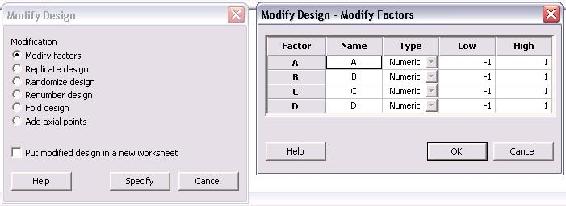
Los factores por defecto se denominan “A”, “B”, “C” y “D” y tienen respectivos niveles altos y bajos de 1 y -1. El nombre de los factores se puede cambiar simplemente haciendo clic en el cuadro y escribiendo un nuevo nombre. Adicionalmente, los niveles bajo y alto para cada factor se pueden modificar en este menú. Dado que los niveles altos y bajos para cada factor pueden no conocerse cuando se crea por primera vez el diseño, es conveniente poder definirlos posteriormente. Haga clic en “Aceptar” después de completar las modificaciones.
Otra modificación típica es agregar réplicas a un diseño. Las réplicas son repeticiones de cada ensayo que ayudan a determinar la reproducibilidad del diseño, aumentando así el número de ensayos y la precisión del DOE. Para agregar réplicas, haga clic en el botón de opción “Replicar diseño” en el menú “Modificar diseño”. Se mostrará el siguiente menú.
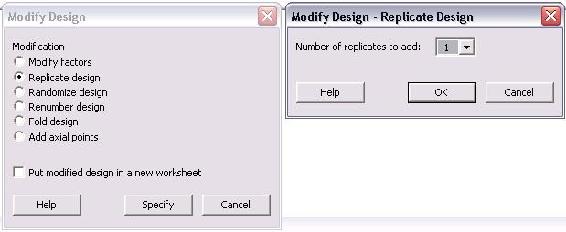
La única opción en este menú es el número de réplicas a agregar. El número oscila entre 1 y 10. Para tener un total de 3 ensayos de cada uno, el usuario debe agregar 2 réplicas en este menú. Si se agregan 4 repeticiones, habrá un total de 5 ensayos de cada uno. Por lo general, si la misma experimentación ocurrirá por 3 periodos de laboratorio, se agregarán 2 repeticiones.
Las modificaciones adicionales al diseño incluyen aleatorización y renumeración del diseño. Se trata de modificaciones muy sencillas que afectan el orden de los juicios. Para obtener información sobre el “Diseño de plegado” y “Agregar puntos axiales”, consulte el menú “Ayuda”.
Análisis de los resultados del DOE
Una vez realizado el estudio completo del DOE, Minitab puede ser utilizado para analizar el efecto de los resultados experimentales (referidos como respuestas) sobre los factores especificados en el diseño. El primer paso para analizar los resultados es ingresar las respuestas en la tabla DOE. Esto se hace de manera muy similar a agregar datos a una hoja de datos de Excel. En las columnas a la derecha del último factor, ingrese cada respuesta como se ve en la siguiente figura.
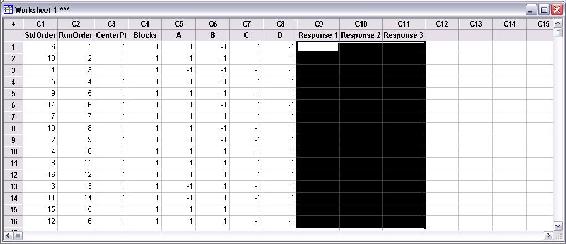
La figura anterior contiene tres columnas de respuesta. Los nombres de cada respuesta se pueden cambiar haciendo clic en el nombre de la columna e ingresando el nombre deseado. En la figura, el área seleccionada en negro es donde se ingresarán las respuestas. Por ejemplo, si la pureza, el rendimiento y la cantidad residual de catalizador se midieron en el estudio DOE, los valores de estos para cada ensayo se ingresarían en las columnas.
Una vez ingresadas las respuestas, se puede realizar un análisis estadístico sobre los datos. Ir a ESTAT>DOE>Factorial>Analizar Diseño Factorial... como se ve en la siguiente imagen.
A continuación se muestra el menú que aparece para analizar el diseño factorial.
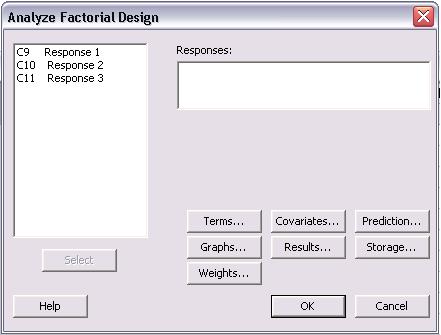
En el menú “Analizar diseño factorial”, las respuestas se muestran a la izquierda de la pantalla. El primer paso es elegir las respuestas a analizar. Todas las respuestas se pueden elegir a la vez o individualmente. Para elegirlos, haga clic (o haga clic y arrastre para seleccionar muchos) y luego haga clic en “Seleccionar” para agregarlos a la sección “Respuestas:” como se ve a continuación.
El siguiente paso es seleccionar qué términos se analizarán para las respuestas. Para ello, da clic en “Términos...” y aparecerá el siguiente menú.
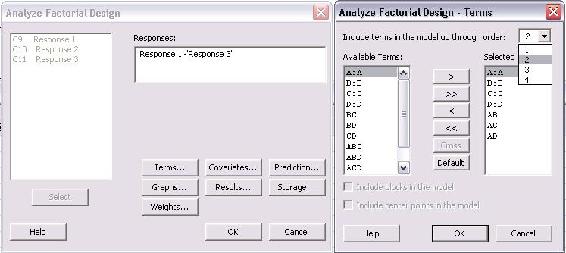
Los tipos de interacciones entre factores se eligen en este menú. Para un modelo de primer orden que excluya todas las interacciones factor a factor, se debe elegir “1" del menú desplegable para “Incluir términos en el modelo hasta el orden:”. Para incluir términos de orden superior y tener en cuenta las interacciones de factores, elija 2, 3 o 4 en el menú desplegable. A menos que se esperen interacciones significativas factor a factor, se recomienda utilizar un modelo de primer orden que sea una aproximación lineal.
Una vez elegidos los términos, el siguiente paso es determinar qué gráficas deben crearse. Los tipos de gráficos se pueden seleccionar haciendo clic en “Gráficos...” en el menú principal “Analizar diseño factorial”.
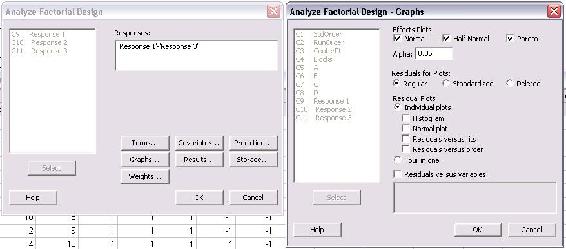
En el menú Gráficos que se muestra arriba, se seleccionaron las tres gráficas de efectos para “Normal”, “Mitad Normal” y “Pareto”. Estas parcelas son diferentes formas de presentar los resultados estadísticos del análisis. Ejemplos de estas gráficas se pueden encontrar en el Ejemplo de Minitab para Análisis de Contactor Centrífugo. El valor alfa, que determina el límite de significación estadística, también se puede elegir en este menú. Por lo general, el valor alfa es 0.05. El último tipo de parcelas que se pueden elegir son las parcelas residuales. Uno común para seleccionar es “Residuales versus ajustes” que muestra cómo la varianza entre los valores predichos del modelo y los valores reales.
La opción final que se debe especificar son los resultados. Haga clic en “Resultados...” en el menú “Analizar diseño factorial” para ver la siguiente pantalla.
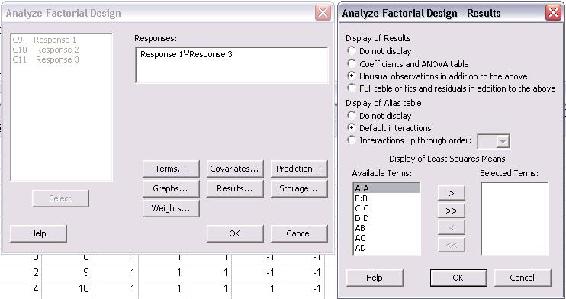
En este menú, selecciona todos los “Términos disponibles” y haz clic en el botón “>>” para moverlos a los “Términos seleccionados”. Esto asegurará que todos los términos serán incluidos en el análisis. Otra característica que se puede seleccionar de este menú es mostrar la “Tabla Coeficientes y ANOVA” para el estudio DOE.
Se pueden seleccionar otras opciones del menú “Analizar diseño factorial” como “Covariables... “, “Predicción... “, “Almacenamiento... “, y “Pesos...”. Consulte el menú “Ayuda” para obtener descripciones de las otras opciones. Una vez que se hayan realizado todos los cambios deseados, haga clic en “Aceptar” para realizar el análisis. Todas las gráficas emergerán en la pantalla y se generará un archivo de texto de los resultados en el archivo de sesión.
Ejemplo de Minitab para análisis de contactores centrífugos
Los contactores centrífugos, también conocidos como contactores centrífugos Podbielniak (POD), se utilizan para purificar una corriente contaminada mediante extracción líquido-líquido a contracorriente. Dos fluidos inmiscibles con diferentes gravedades específicas se ponen en contacto a contracorriente y el soluto de la corriente sucia es extraído por la corriente limpia. Un uso común para la eliminación de metanol de los POD del biodiesel al poner en contacto la corriente con agua. La cantidad de metanol restante en el biodiesel (% en peso de MeOH) después de la purificación y el número de etapas teóricas (No. Theor. Etapas) obtenidas dependen de las condiciones de operación del POD. Los cuatro parámetros principales de operación del POD son velocidad de rotación (RPM), relación de biodiesel a agua (Ratio), caudal total de biodiesel y agua (Caudal) y presión (Presión). Se ha realizado un estudio DOE para determinar el efecto de las cuatro condiciones de operación sobre las respuestas de% en peso de MeOH en biodiesel y número de etapas teóricas logradas. (NOTA: Los datos reales para este ejemplo fueron maquillados)
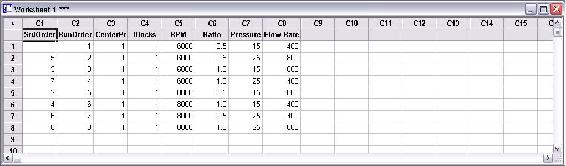
Se creó un estudio DOE de 4 factores y 2 niveles usando Minitab. Debido a que los experimentos del POD consumen mucho tiempo, se utilizó un diseño de media fracción de 8 ensayos. La siguiente figura contiene la tabla de ensayos para el DOE.
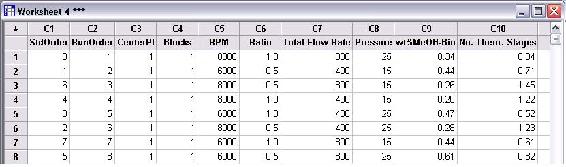
Después de realizar todos los ensayos, se calculó el% en peso de metanol restante en el biodiesel y el número de etapas teóricas logradas. La siguiente figura contiene la tabla de ensayos del DOE que incluye las dos respuestas.
Se realizó un análisis en el estudio DOE para determinar los efectos de cada factor en las respuestas. Solo se incluyeron términos de primer orden en el análisis para crear un modelo lineal. A continuación se muestran los gráficos de Pareto para el% en peso de MeOH en biodiesel y el número de etapas teóricas.
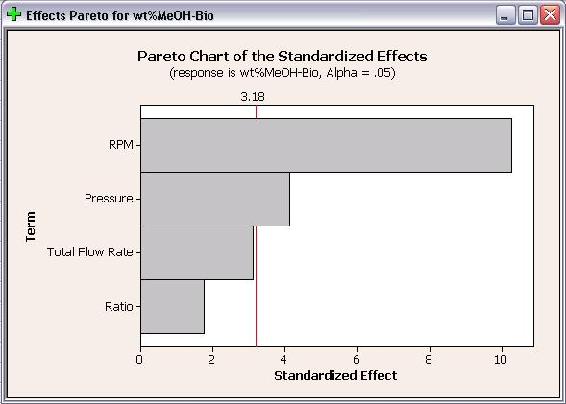
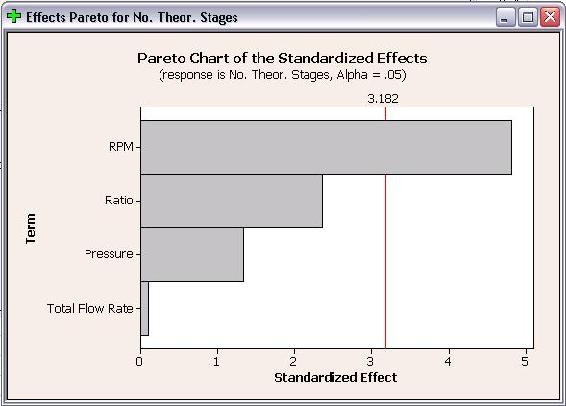
Los gráficos de Pareto muestran qué factores tienen efectos estadísticamente significativos en las respuestas. Como se ve en las gráficas anteriores, RPM tiene efectos significativos para ambas respuestas y la presión tiene un efecto estadísticamente significativo sobre el% de metanol en biodiesel. Ni el caudal ni la relación tienen efectos estadísticamente significativos en ninguna de las respuestas. Los gráficos de Pareto son gráficos de barras que permiten a los usuarios ver fácilmente qué factores tienen efectos significativos.
A continuación se muestran las gráficas de mitad normal para% en peso de metanol en biodiesel y número de etapas teóricas.
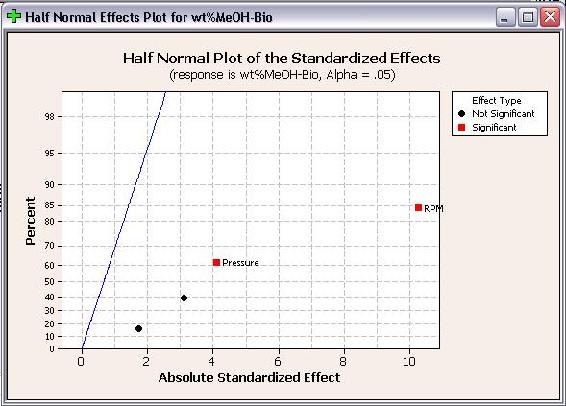
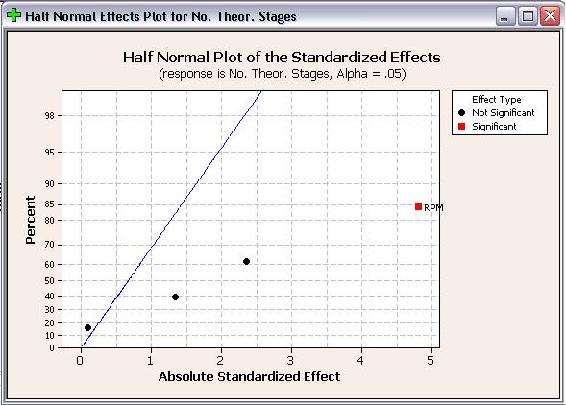
Al igual que las parcelas de Pareto, las parcelas Half Normal muestran qué factores tienen efectos significativos en las respuestas. Los factores que tienen efectos significativos se muestran en rojo y los que no tienen efectos significativos se muestran en negro. Cuanto más lejos esté un factor de la línea azul, más significativo tendrá el efecto sobre la respuesta correspondiente. Para% de metanol en biodiesel, RPM está más lejos de la línea azul que la presión, lo que indica que RPM tiene un efecto más significativo sobre el% de metanol en biodiesel que la presión.
La trama final creada es la Gráfica de Efecto Normal. La Parcela Normal es similar a la parcela Half Normal en diseño. Sin embargo, la Gráfica Normal muestra si el efecto del factor es positivo o negativo sobre la respuesta. A continuación se muestran las Gráficas Normales para las respuestas.
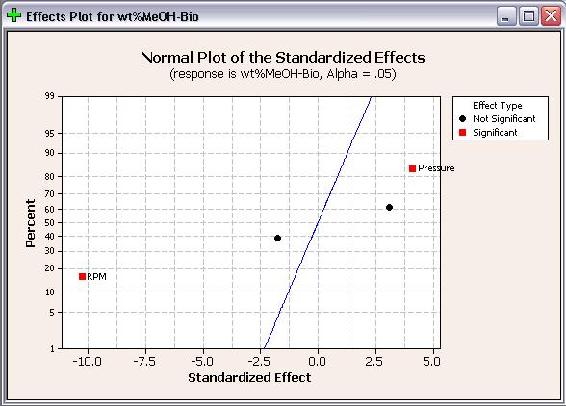
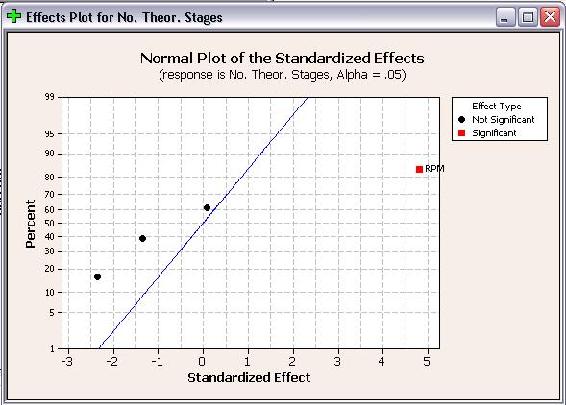
Como se vio anteriormente, las RPM se muestran con un efecto positivo para el número de etapas teóricas, pero un efecto negativo para% en peso de metanol en biodiesel. Un efecto positivo significa que a medida que aumenta la RPM, aumenta el número de etapas teóricas. Mientras que un efecto negativo indica que a medida que aumentan las RPM, disminuye el% en peso de metanol en el biodiesel. Afortunadamente para operar con el POD, estos son resultados deseados. Al elegir las condiciones de operación para el POD, se deben maximizar las RPM para minimizar el metanol residual en el biodiesel y maximizar el número de etapas teóricas logradas.
Además de las gráficas de efectos anteriores, Minitab calcula los coeficientes y constantes para las ecuaciones de respuesta. Las ecuaciones de respuesta se pueden utilizar como modelos para predecir respuestas en diferentes condiciones de operación (factores). A continuación se muestran los coeficientes y constantes para% de metanol en biodiesel y número de etapas teóricas.
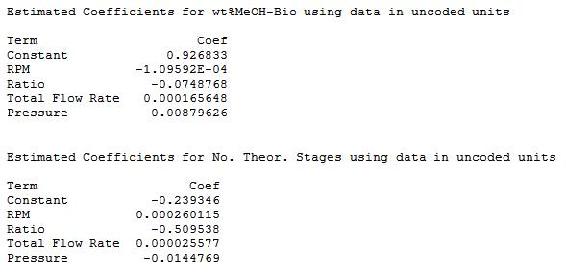
Dado que se trata de un modelo lineal de primer orden, los coeficientes se pueden combinar con los parámetros operativos para determinar ecuaciones. A continuación se muestran las ecuaciones de este modelo.
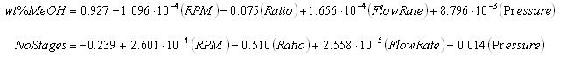
Estas ecuaciones se pueden utilizar como modelo predictivo para determinar el% en peso de metanol en biodiesel y el número de etapas teóricas logradas en diferentes condiciones de operación sin realizar realmente los experimentos. Sin embargo, los límites del modelo deben probarse antes de que el modelo se use para predecir respuestas en muchas condiciones de operación diferentes.
Has sido empleado de SuperGym, un gimnasio local de entrenamiento personal, que quiere la perspectiva de un ingeniero sobre cómo ofrecer los mejores planes a sus clientes. SuperGym actualmente categoriza a sus clientes en 4 tipos de cuerpo para ayudar a planificar el mejor programa posible.
- Tipo 1 - Muy saludable
- Tipo 2 - Necesita tono
- Tipo 3 - Necesita fuerza
- Tipo 4 - Necesita tono y fuerza
Además, SuperGym ofrece 4 planes de entrenamiento diferentes, de la A a la D, ninguno de los cuales está atendido directamente a ninguno de los diferentes tipos. Crear un diseño factorial experimental que pueda ser utilizado para probar los efectos de los diferentes planes de entrenamiento en los diferentes tipos de personas en el gimnasio.
Solución
Para resolver este problema, necesitamos determinar cuántos experimentos diferentes necesitarían realizarse. Para resolver esto, podemos ver que tenemos dos factores diferentes, tipo de cuerpo y plan de entrenamiento. Para cada factor, existen cuatro niveles diferentes. Así, tenemos un diseño factorial 4 2, lo que nos da 16 grupos experimentales diferentes. Creando una tabla de todos los diferentes grupos, llegamos al siguiente diseño factorial:
| A1 | B1 | C1 | D1 |
| A2 | B2 | C2 | D2 |
| A3 | B3 | C3 | D3 |
| A4 | B4 | C4 | D4 |
Donde A-D es el plan de entrenamiento y 1-4 son los tipos
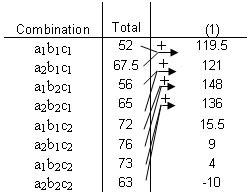
Supongamos que está buscando estudiar los efectos de las horas dormidas (A), las horas pasadas con otra pareja (B) y las horas dedicadas a estudiar (C) en los puntajes de un examen de estudiantes. Se le da la siguiente tabla que relaciona la combinación de estos factores y las puntuaciones de los estudiantes a lo largo de un semestre. Utilizar el método Yates para determinar el efecto de cada variable en el desempeño de los alumnos en el curso.
| 1 | 17 | 24 | 19 | 21 | 22 | 28 | 25 | 24 |
|---|---|---|---|---|---|---|---|---|
| 2 | 18.5 | 21 | 20 | 19 | 26 | 22 | 27 | 19 |
| 3 | 16.5 | 22.5 | 22 | 25 | 24 | 26 | 21 | 20 |
| Total | 52 | 67.5 | 61 | 65 | 72 | 76 | 73 | 63 |
Solución
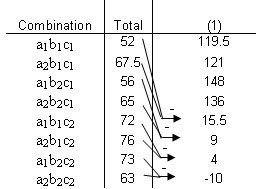
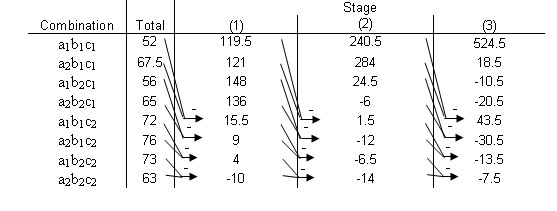
Utilizando el enfoque introducido anteriormente en este artículo, llegamos a la siguiente solución de Yates.
| Escenario | Total principal | ||||
| Combinación | Total | 1 | 2 | 3 | Efecto Factorial |
| a 1 b 1 c 1 | 52 | 119.5 | 245.5 | 529.9 | No importa |
| a 2 b 1 c 1 | 67.5 | 126 | 284 | 13.5 | A |
| a 1 b 2 c 1 | 61 | 148 | 19.5 | -5.5 | B |
| a 2 b 2 c 1 | 65 | 136 | -6 | -25.5 | AB |
| a 1 b 1 c 2 | 72 | 15.5 | 6.5 | 38.5 | C |
| a 2 b 1 c 2 | 76 | 4 | -12 | -25.5 | AC |
| a 1 b 2 c 2 | 73 | 4 | -11.5 | -18.5 | BC |
| a 2 b 2 c 2 | 63 | -10 | -14 | -2.5 | ABC |
De esta tabla, podemos ver que hay correlación positiva para los factores A y C, es decir, que más sueño y más estudio lleva a una mejor calificación de prueba en la clase. El factor B, sin embargo, tiene un efecto negativo, lo que significa que pasar tiempo con su pareja conduce a una peor puntuación en la prueba. La lección aquí, por lo tanto, es pasar más tiempo durmiendo y estudiando, y menos tiempo con tu novio o novia.
Tu mamá está cultivando un huerto para la feria estatal y ha hecho algunos experimentos para encontrar la condición de cultivo ideal para sus verduras. Ella te pide ayuda para interpretar los resultados y te muestra los siguientes datos:
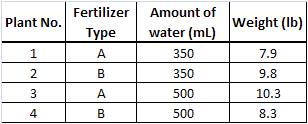
Hacer gráficas para determinar los efectos principales o de interacción de cada factor.
Solución
Aquí está la trama que deberías haber obtenido para los datos dados.
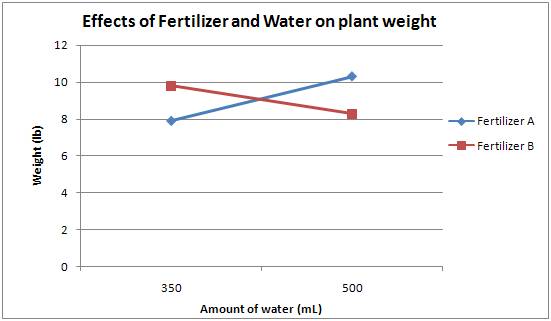
De esto se puede ver que hay un efecto de interacción ya que las líneas se cruzan. No se pueden discutir los resultados sin hablar tanto del tipo de fertilizante como de la cantidad de agua utilizada. El uso del fertilizante A y 500 mL de agua resultó en la planta más grande, mientras que el fertilizante A y 350 mL dieron la planta más pequeña. El Fertilizante B y 350 mL dieron la segunda planta más grande, y el fertilizante B y 500 mL dieron la segunda planta más pequeña. Claramente existe una interacción debido a la cantidad de agua utilizada y al fertilizante presente. Quizás cada fertilizante sea más efectivo con una cierta cantidad de agua. En cualquier caso, tu mamá tiene que considerar tanto el tipo de fertilizante como la cantidad de agua que se proporciona a las plantas al momento de determinar las condiciones de crecimiento adecuadas.
¿Cuál de las siguientes no es una ventaja del uso del diseño factorial sobre el diseño de un factor?
- Más eficiente en el tiempo
- Proporciona cómo cada factor afecta la respuesta
- No requiere pruebas explícitas
- No requiere regresión
- Contestar
-
TBA
En un experimento de diseño factorial 2 2, se obtiene un valor total del efecto principal de -5. Esto significa que
- existe una correlación positiva relativa entre los dos factores
- no hay correlación entre los dos factores
- existe una correlación negativa relativa entre los dos factores
- existe una correlación relativa positiva o negativa entre los dos factores
- Contestar
-
TBA
Referencias
- Box, George E.P., et. al. “Estadísticas para ingenieros: una introducción al diseño, análisis de datos y construcción de modelos”. Nueva York: John Wiley & Sons.
- Trochim, William M.K. 2006. “Diseños Factoriales”. Base de Conocimientos de Métodos de Investigación. < http://www.socialresearchmethods.net/kb/expfact.htm >
- Pérez, José A., et. al. “Efecto de las variables del proceso sobre el pretratamiento de agua caliente líquida de paja de trigo para la bioconversión a combustible-etanol en un reactor discontinuo”. Revista de Tecnología Química y Biotecnología. Tomo 82, Número 10, Páginas 929-938. Publicado En línea Sep 3, 2007.


