1.7: Linealización de modelos no lineales

Linealización de funciones no lineales

El comportamiento de un sistema no lineal, descrito por\(y=f(x)\), en las proximidades de un punto operativo dado\(x=x_0\), se puede aproximar trazando una línea tangente a la gráfica de\(f\left(x\right)\) en ese punto.

Analíticamente, la linealización de una función no lineal implica la expansión de la serie Taylor de primer orden sobre el punto operativo.

Let\(\delta x=x-x_0\) representa la variación desde el punto operativo; entonces la serie Taylor de una función de variable única se escribe como:

\[f\left(x_0+\delta x\right)=f\left(x_0\right)+\frac{\partial f\left(x_0\right)}{\partial x}\delta x+\dots\]

El modelo de primer orden resultante se describe por:

\[f\left(x\right)-f\left(x_0\right)=\frac{\partial f\left(x_0\right)}{\partial x}(x-x_0)\]

Ejemplo\(\PageIndex{1}\)

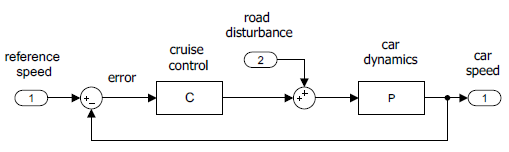
Considere que un vehículo conducido en el control de crucero están representados por el diagrama de bloques (Figura 1.7.1). Las fuerzas que actúan sobre el automóvil incluyen su peso, la fuerza motriz generada por el par motor aplicado a las ruedas, la resistencia aerodinámica y la fricción de rodadura del neumático a la superficie.

El vehículo pesa\(1440kg\) y se conduce a\(20m/s\) (aproximadamente 45 mph). El vehículo experimenta arrastre aerodinámico:\(F_d=\frac{1}{2}\rho v^2Ac_d\). Suponiendo\(\rho =1.2\ kg/m^3\) (para el aire),\(A=4m^2\), y\(c_d=.25\), da como resultado una fuerza de arrastre no lineal:\(F_d=0.6v^2N\).

Una expansión de primer orden de la serie Taylor de la fuerza de arrastre sobre la velocidad de crucero (\(20\ m/s\)) se da como:

\[F_d(v)=F_d \left(20\right) + {\left. F^\prime_d\right|}_{v=20} (v-20).\]

Dejar\(\delta F_d=F_d-F_d\left(20\right),\ \ \delta v=v-20,\) denotar las variaciones en la fuerza y velocidad; entonces, el modelo linealizado para la fuerza de arrastre se da como:

\[\delta F_d=24\delta v.\]

Además, las llantas generan una fuerza de fricción:\(F_r=0.015W\), donde\(W\) esta el peso del auto. Para\(m=1440kg\) y\(g=9.8m/s^2\), la fricción del neumático es:\(F_r=212N\).

Dejar\(T_e=rF_e\) denotar el par motor, donde\(F_e\) está la salida de fuerza y\(r=0.33m\) es el radio de la rueda; entonces, la ecuación dinámica del vehículo se da como:

\[T_e/r-F_r-F_d=m\frac{dv}{dt} \]

Sustituir los valores de los parámetros anteriores da como resultado:

\[m\frac{dv}{dt}+0.6v^2=3T_e-212.\]

Dejar\(\delta T_e\) denotar la variación en el par motor; entonces, un modelo linealizado del vehículo de crucero en\(20m/s\) se da como:

\[1440\frac{d\delta v}{dt}+24\delta v=3\delta T_e \]

Figura\(\PageIndex{1}\): Diagrama de bloques del sistema de control de crucero del vehículo.

Linealización de Modelos de Variables de Estado

Supongamos que el modelo de variable de estado no lineal de un sistema de entrada única y salida única (SISO) se describe mediante las siguientes ecuaciones:

\[\dot{x}(t)=f(x,u)\]

\[y(t)=g(x,u)\]

donde\(x\) es un vector de variables de estado,\(u\) es una entrada escalar,\(y\) es una salida escalar,\(f\) es una función vectorial de las variables de estado y de entrada, y\(g\) es una función escalar de esas variables.

Un punto estacionario para el modelo se define por:\(f(x_{ e} ,u_ e )=0\). Las desviaciones del punto estacionario se expresan como:\(x(t)=x_{ e} (t)+\delta x(t);\, \, \, u(t)=u_ e (t)+\delta u(t)\).

En cuanto a las variaciones:\(\delta x,\delta u\), el modelo linealizado del sistema se expresa como:

\[\dot{\delta }x(t)=\left[\partial f_{i} /\partial x_{j} \right]|_{(x_{ e} ,u_{ e} )} \delta x(t)+\left[\partial f_{i} /\partial u\right]|_{(x_{ e} ,u_{ e} )} u(t)\]

\[y(t)=\left[\partial g/\partial x_{j} \right]|_{(x_{e} ,u_{e} )} \delta x(t)+\left[\partial g/\partial u\right]|_{(x_{e} ,u_{e} )} \delta u(t),\]

donde\([\partial f_{i} /\partial x_{j} ]\) es una matriz jacobiana de derivados parciales;\([\partial f_{i} /\partial u],[\partial g/\partial x_{j} ]\) son vectores de derivados parciales, y\([\partial g/\partial u]\) es una derivada parcial escalar; todas las derivadas se computan en el punto estacionario.

El modelo linealizado se expresa en su forma familiar vector-matriz como:

\[\dot{\delta }x(t)=A\delta x(t)+bu(t)\]

\[y(t)=c^{ T} \delta x(t)+d\delta u(t).\]

En lo anterior,\(A\) representa una matriz de\(n\times n\) sistema,\(b\) es un vector de\(n\times 1\) columna de distribuciones de entrada,\(c^{ T}\) es un vector de\(1\times n\) fila de contribuciones de salida, y d es una ganancia escalar.

Ejemplo\(\PageIndex{2}\)

El modelo de un péndulo simple se describe mediante la ecuación dinámica:

\[ml^{2} \ddot{\theta }(t)+mgl\; \sin \theta (t)=T(t),\]

donde\(\theta (t)\) está el ángulo del péndulo,\(T(t)\) es el par aplicado;\(m,l\) representan la masa y la longitud del péndulo, y\(g\) es la constante gravitacional.

Al usar\((\theta ,\; \omega )\) como variables de estado para el péndulo, el modelo no lineal se expresa como:

\[\frac{d}{dt} \left(\begin{array}{c} {\theta } \\ {\omega } \end{array}\right)=\left(\begin{array}{c} {\omega } \\ {-\frac{g}{l} \sin \theta } \end{array}\right)+\left(\begin{array}{c} {0} \\ {T(t)} \end{array}\right).\]

La matriz jacobiana para el péndulo simple se expresa como:

\[\left[\frac{\partial f}{\partial x}\right]=\left(\begin{array}{cc} {0} & {1} \\ {-\frac{g}{l} \cos \theta \; } & {0} \end{array}\right).\]

Se pueden identificar dos puntos de equilibrio en el caso de un péndulo simple:\(\theta _{ e} =0^{\circ } ,\; 180^{\circ }\). Los modelos linealizados definidos en los puntos de equilibrio se dan como:

\[{\theta }_e=0{}^\circ : \frac d{ dt} \left[\begin{array}{c} {\theta } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-\frac{g}{l} } & {0} \end{array}\right]\left[\begin{array}{c} {\theta } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]T\]

\[{\theta }_e=180{}^\circ : \frac d{ dt} \left[\begin{array}{c} {\theta } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {\frac{g}{l} } & {0} \end{array}\right]\left[\begin{array}{c} {\theta } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]T\]

La ecuación de salida en ambos casos se da como:\(\theta \left(t\right)=\left[ \begin{array}{cc} 1 & 0 \end{array} \right]\left[ \begin{array}{c} \theta \\ \omega \end{array} \right]\).