2.5: Respuesta sinusoidal de un sistema
- Page ID
- 84959
Respuesta a la entrada sinusoidal
La respuesta sinusoidal de un sistema se refiere a su respuesta a una entrada sinusoidal:\(u(t)=\cos \; \omega _{0} t\) o\(u(t)=\sin \; \omega _{0} t\).
Para caracterizar la respuesta sinusoidal, podemos asumir una entrada exponencial compleja de la forma:\(u\left(t\right)=e^{j{\omega }_0t},\ \ u\left(s\right)=\frac{1}{s-j{\omega }_0}\). Entonces, la salida del sistema se da como:\(\ y\left(s\right)=\frac{G\left(s\right)}{s-j{\omega }_0}\).
Para proceder, vamos\(G\left(s\right)=\frac{n(s)}{\prod^n_{i=1}{\left(s-p_i\right)}}\), donde\(p_i,\ i=1,\dots n\), denotan los polos de la función de transferencia; luego, usando PFE, la respuesta del sistema se da como:
\[y\left(s\right)=\frac{A_0}{s-j{\omega }_0}+\sum^n_{i=1}{\frac{A_i}{s-p_i}}\]
donde\(A_0=G\left(j{\omega }_0\right)\). El tiempo de respuesta del sistema se da como:\[y\left(t\right)=G\left(j{\omega }_0\right)e^{j{\omega }_0t}+\sum^n_{i=1}{A_ie^{p_it}}\]
Suponiendo estabilidad BIBO, es decir\(Re\left[p_i\right]<0\), el componente de respuesta transitoria se extingue con el tiempo. Entonces, la respuesta en estado estacionario se describe como:\[y_{ss}(t)=G\left(j{\omega }_0\right)e^{j{\omega }_0t}\]
Definición: Función de respuesta de frecuencia
La función de respuesta de frecuencia, para una función de transferencia dada\(G(s)\) se define como:\(G(j\omega )=G(s)|_{s=j\omega }\).
La función de respuesta de frecuencia se describe en la forma de fase de magnitud como:\(G(j\omega )=\left|G(j\omega )\right|e^{\angle G(j\omega )} .\)
Cuando se calcula a una frecuencia particular,\(\omega ={\omega }_0\), la función de respuesta de frecuencia,\(G\left(j{\omega }_0\right)\) es un número complejo.
Entonces, la respuesta de estado estacionario a una sinusoide compleja\(u(t)=e^{j\omega _{0} t}\) se da como:\[y_{ss} (t)=\left|G(j\omega _{0} )\right|e^{\angle G(j\omega_0 )} e^{j\omega _{0} t}\]
Por la identidad de Euler, tenemos:\(e^{j\omega _{0} t} =\cos \left(\omega _{0} t\right)+j\,\;\sin \left(\omega _{0} t\right)\); por lo tanto, la respuesta de estado estacionario a\(u(t)=\cos \, \omega _{0} t\) se da como:\[y_{\rm ss} (t)=\left|G(j\omega _{0} )\right|\cos (\omega _{0} t+\angle G(j\omega _{0} ))\]
Del mismo modo, la respuesta en estado estacionario a\(u(t)=\sin \, \omega _{0} t\) se da como:\[y_{\rm ss} (t)=\left|G(j\omega _{0} )\right|\,\sin (\omega _{0} t+\angle G(j\omega _{0} ))\]
Así, la respuesta de estado estacionario a la sinusoide de una cierta frecuencia es una sinusoide a la misma frecuencia, escalada por la magnitud de la función de respuesta de frecuencia; la respuesta incluye una contribución de fase de la función de respuesta de frecuencia.
Ejemplos
Ejemplo\(\PageIndex{1}\)
Un modelo de motor de CC pequeño se aproxima como:\(G\left(s\right)=\frac{500}{\left(s+10\right)\left(s+100\right)}\).
Su función de respuesta de frecuencia se da como:\(G\left(j\omega \right)=\frac{0.5}{\left(0.01\omega +1\right)\left(0.1\omega +1\right)}\).
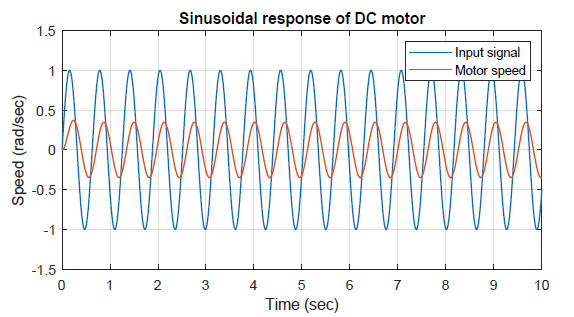
Dejar\(u(t)=\sin 10t\); entonces, en el estado estacionario, la respuesta sinusoidal se da como:\(y_{ss}\left(t\right)=0.35\;{\sin \left(10t-50{}^\circ \right)\ }\).
La respuesta sinusoidal del motor de CC se representa en la Figura 2.5.1.
Ejemplo\(\PageIndex{2}\)
El modelo de un sistema masa-resorte-amortiguador se da como:\(G\left(s\right)=\frac{1}{s^2+2s+5}=\frac{1}{{\left(s+1\right)}^2+2^2}\); los polos complejos se encuentran en:\(s=-1\pm j2\).
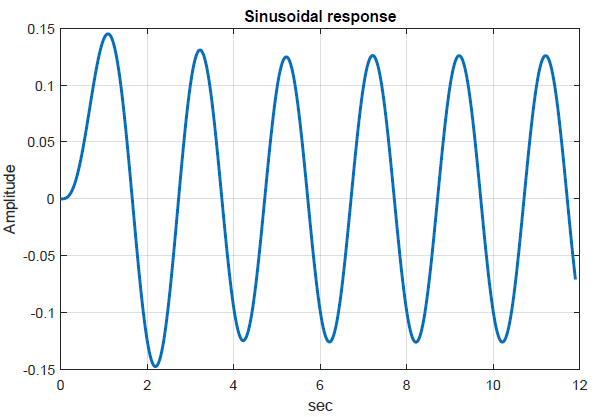
Dejemos\(u(t)=\sin \; \pi t\); entonces, en el estado estacionario, tenemos:\(y_{ss}\left(t\right)=0.126\;{\sin \left(\pi t-128{}^\circ \right)\ }\).
La respuesta se grafica a continuación e incluye la respuesta transitoria, que se extingue en 4-5 seg.
Visualización de la respuesta de frecuencia
La función de respuesta de frecuencia se da en forma polar como:\(G(j\omega )=|G(j\omega )|e^{j\phi (\omega )}\).
Como\(\omega\) varía de\(0\) a\(\infty\), tanto la magnitud como la fase pueden representarse como funciones de\(\omega\).
Se acostumbra trazar tanto la magnitud como la fase en contra\({\log \;\omega \ }\), lo que le da un alto rango dinámico a\(\omega\). Además, la magnitud se grafica en decibelios como:\(|G(j\omega )|_{\rm dB} =20\; \log _{10} |G(j\omega )|\). La fase\(\phi (\omega )\) se traza en grados. Las gráficas de respuesta de frecuencia resultantes se conocen comúnmente como parcelas de Bode.
A continuación se ilustra el trazado de la respuesta de frecuencia en el caso de sistemas de primer y segundo orden.
Sistema de primer orden
Vamos\(G(s)=\frac{K}{\tau s+1} \;\); entonces\(G\left(j\omega \right)=\frac{K}{1+j\omega \tau }\); Por lo tanto,
\[{\left|G\left(j\omega \right)\right|}_{\rm dB}=20\;{\log K\ }-20\;{\log \left|1+j\omega \tau \right|\ },\;\;\; \angle G\left(j\omega \right)=-{{\tan}^{-1} \omega \tau \ }\]
Ejemplo\(\PageIndex{3}\)
Se\(G\left(s\right)=\frac{1}{s+1}\) trazan las gráficas de magnitud y fase de Bode (Figura 2.5.3).
La parcela de magnitud se caracteriza por:\(G\left(j0\right)=0 \;{\rm dB},\ \ G\left(j1 \right)=-3 \;{\rm dB}\), y una\(-20 \;{\rm dB}/{\rm decade}\) pendiente para grandes\(\omega\).
La gráfica de fase se caracteriza por:\(G\left(j0\right)=0{}^\circ ,\ G\left(j{0.1}\right)=-5.7{}^\circ ,\ G\left(j1\right)=-45{}^\circ ,\ \ G\left(j10\right)=-84.3{}^\circ ,\ G\left(j\infty \right)=-90{}^\circ\).
Sistema de primer orden con integrador
Vamos\(G(s)=\frac{K}{s\left(\tau s+1\right)}\); entonces\(G\left(j\omega \right)=\frac{K}{j\omega \left(1+j\omega \tau \right)}\); Por lo tanto,
\[{\left|G\left(j\omega \right)\right|}_{\rm dB}=20\;{\log K\ }-20\;{\log \omega \ }-20\;{\log \left|1+j\omega \tau \right|\ }\]
\[\angle G\left(j\omega \right)=-{{\tan}^{-1} \omega \tau \ }-90{}^\circ \]
Ejemplo\(\PageIndex{4}\)
Las gráficas de magnitud y fase de Bode\(G\left(s\right)=\frac{1}{s\left(s+1\right)}\) se trazan a continuación.
La gráfica de magnitud se caracteriza por una pendiente inicial de\(-20 \;{\rm dB}/{\rm decade}\) que cambia a\(-40 \;{\rm dB}/{\rm decade}\) para grande\(\omega\); en la frecuencia de esquina,\(G\left(j1 \right)=-3 \;{\rm dB}\).
La gráfica de fase se caracteriza por:\(G\left(j0\right)=-90{}^\circ ,\ G\left(j{0.1}\right)=-96{}^\circ ,\ G\left(j1\right)=-135{}^\circ ,\ \ G\left(j10\right)=-174.3{}^\circ ,\ G\left(j\infty \right)=-180{}^\circ\).
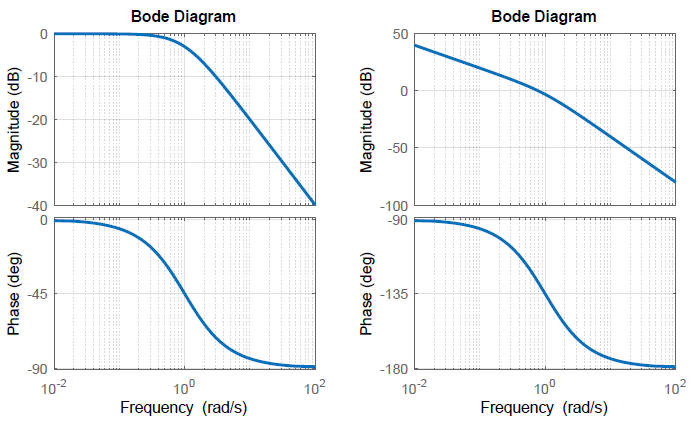
Sistema de segundo orden con postes reales
Vamos\(G(s)=\frac{K}{(\tau _{1} s+1)(\tau _{2} s+1)}\); entonces\(G\left(j\omega \right)=\frac{K}{\left(1+j\omega {\tau }_1\right)\left(1+j\omega {\tau }_2\right)}\); Por lo tanto,
\[{\left|G\left(j\omega \right)\right|}_{\rm dB}=20\;{\log K\ }-20\;{\log \left|1+j\omega {\tau }_1\right|\ }-20\;{\log \left|1+j\omega {\tau }_2\right|\ }\]
\[\angle G\left(j\omega \right)=-{{\tan}^{-1} \omega {\tau }_1\ }-{{\tan}^{-1} \omega {\tau }_2\ }\]
Ejemplo\(\PageIndex{5}\)
Las gráficas de magnitud y fase de Bode\(G\left(s\right)=\frac{2}{\left(s+1\right)\left(s+2\right)}\) se representan en la Figura 2.5.4.
La gráfica de magnitud se caracteriza por:\(G\left(j0\right)=0 \;{\rm dB},\ \ G\left(j1\right)=-3 \;{\rm dB}\), una pendiente intermedia de\(-20 \;{\rm dB}/{\rm decade}\)\(G\left(j2\right)=-14 \;{\rm dB}\), y una pendiente de\(-40 \;{\rm dB}/{\rm decade}\) para grandes\(\omega\).
La gráfica de fase se caracteriza por:\(G\left(j0\right)=0{}^\circ ,\ G\left(j1\right)=-45{}^\circ ,\ \ G\left(j2\right)=-135{}^\circ ,\ \ G\left(j\infty \right)=-180{}^\circ\).
Sistema de segundo orden con polos complejos
Dejar\(G\left(s\right)=\frac{{\omega }^2_n}{s^2+2\zeta {\omega }_ns+{\omega }^2_n}\); entonces\(G\left(j\omega \right)=\frac{{\omega }^2_n}{{\omega }^2_n-{\omega }^2+j2\zeta \omega {\omega }_n}\), donde\({\omega }_n\) y\(\zeta\) representar la frecuencia natural y la relación de amortiguación. Por lo tanto,
\[{\left|G\left(j\omega \right)\right|}_{\rm dB}=-20\;{{\log}_{10} \left|1-{\left(\frac{\omega }{{\omega }_n}\right)}^2+j2\zeta \left(\frac{\omega }{{\omega }_n}\right)\right|\ }\]
\[\phi \left(\omega \right)={{\tan}^{-1} \left(\frac{2\zeta \left(\frac{\omega }{{\omega }_n}\right)}{\left[1-{\left(\frac{\omega }{{\omega }_n}\right)}^2\right]}\right)\ }\]
Ejemplo\(\PageIndex{6}\)
Las gráficas de magnitud y fase de Bode\(G(s)=\frac{10}{s^{2} +2s+10}\) se trazan a continuación.
La parcela de magnitud se caracteriza por:\(G\left(j0\right)=0 \;{\rm dB},\ \ G\left(j{\omega }_n\right)=-20\;{\log \left(2\zeta \right)\ }\), y una\(-40 \;{\rm dB}/{\rm decade}\) pendiente para grandes\(\omega\).
La gráfica de fase se caracteriza por:\(\phi \left(j0\right)=0{}^\circ ,\ \ \phi \left(j{\omega }_n\right)=-90{}^\circ ,\ \ \phi \left(j\infty \right)=-180{}^\circ\).
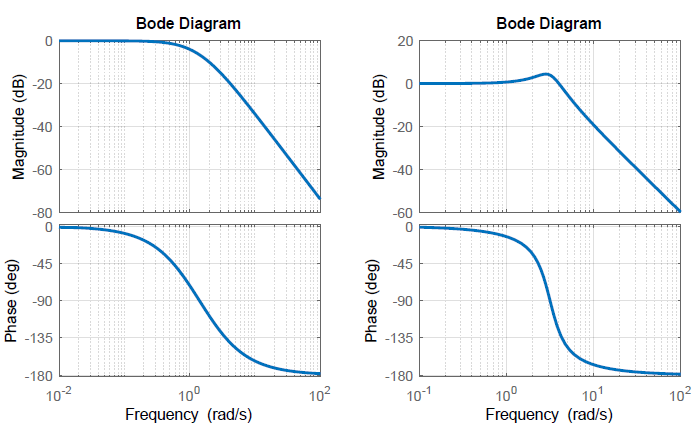
Pico de Resonancia en la Respuesta de Frecuencia
La gráfica de magnitud Bode de una función de transferencia con polos complejos y baja amortiguación muestra un pico distintivo en la gráfica de magnitud Bode a la frecuencia resonante,\({\omega }_r\); la frecuencia resonante y la magnitud del pico se calculan como:
\[\omega _{r} =\omega _{n} \sqrt{1-2\zeta ^{2} } ,\; \; \zeta <\frac{1}{\sqrt{2} }\]
\[M_{\rm p\omega } =\frac{1}{2\zeta \sqrt{1-\zeta ^{2} } } ,\; \; \zeta <\frac{1}{\sqrt{2} } \]
Ejemplo\(\PageIndex{7}\)
Vamos\(G(s)=\frac{10}{s^{2} +2s+10}\); entonces, tenemos:\(\omega _{n} =\sqrt{10} \; \frac{\rm rad}{\rm sec} ,\; \, \zeta =\frac{1}{\sqrt{10} } ,\, \; \omega _{r} =8\; \frac{\rm rad}{\rm sec} ,\;\) y\(M_{\rm p\omega } =1.67\) o\(4.44\; \rm dB\) (Figura 2.5.4).
Relacionar la respuesta de tiempo y frecuencia
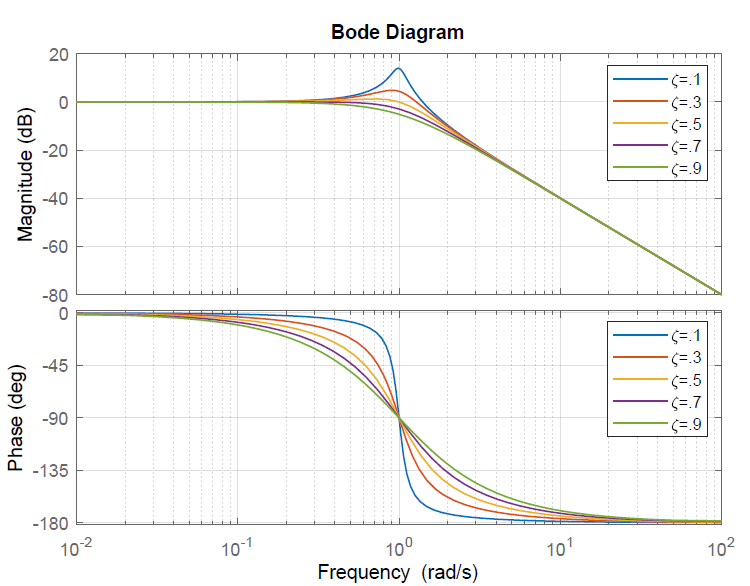
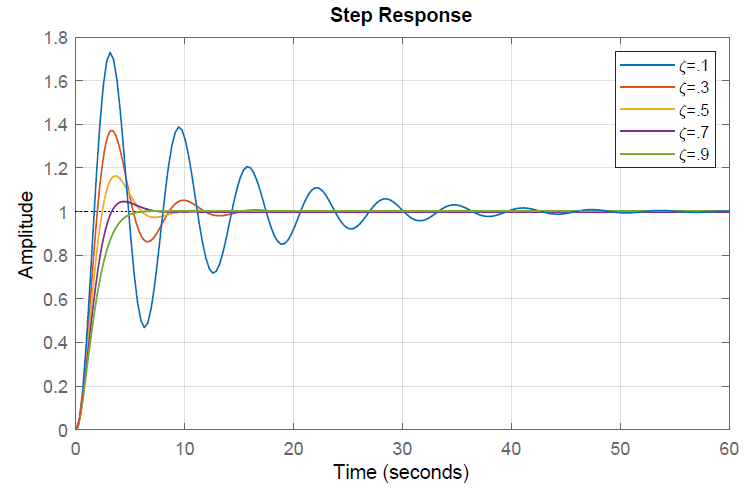
Cuando la función de transferencia del sistema tiene polos con una relación de amortiguación baja, la gráfica de magnitud Bode muestra un pico resonante. Al mismo tiempo, la respuesta escalonada del sistema muestra oscilaciones.
Para ilustrar esta relación, consideramos un prototipo de sistemas de segundo orden:\(G(s)=\frac{1}{s^{2} +2\zeta s+1}\), dónde\(\omega _{n} =1\),\(\zeta \in \left\{0.1,\, 0.3,\, 0.5,\, 0.7,\, 0.9\right\}\).
La respuesta de frecuencia y la respuesta de paso de unidad de dominio de tiempo para las funciones de transferencia de segundo orden con\(\omega _{n} =1\) para los diversos valores de\(\zeta \in \left\{0.1,\, 0.3,\, 0.5,\, 0.7,\, 0.9\right\}\) se representan a continuación.