2.4: La respuesta escalonada

Step Response

Las entradas de impulso y paso se encuentran entre las entradas prototipo utilizadas para caracterizar la respuesta de los sistemas. La entrada unidad-paso se define como:

\[ u(x)=\begin{cases}0, &\;x<0 \\ 1,&\; x\ge 0\end{cases} \]

Definición: Step Response

La respuesta escalonada de un sistema se define como su respuesta a una entrada de paso de unidad\(u(t)\), o\(u(s)=\frac{1}{s}\).

Vamos a\(G(s)\) describir la función de transferencia del sistema; entonces, la respuesta unidad-paso se obtiene como:\(y(s)\, \, =\, \, G(s)\frac{1}{s}\).

Su transformación inversa de Laplace conduce a:\(y\left(t\right)={\mathcal{L}}^{-1}\left[\frac{G\left(s\right)}{s}\right]\).

Alternativamente, la respuesta escalonada se puede obtener integrando la respuesta de impulso:\(y(t)=\int_0^t g(t-\tau)d\tau\).

La respuesta unidad-paso de un sistema estable parte de algún valor inicial:\(y\left(0\right)=y_0\), y se establece en un valor de estado estacionario:\(y_{\infty }={\lim_{t\to \infty } y\left(t\right)\ }\).

Además, a partir de la aplicación del teorema del valor final (FVT):\(y_{\infty }=G{\left(s\right)|}_{s=0}\).

Respuesta escalonada de sistemas de orden bajo

A continuación se describe la respuesta unidad-paso en el caso de los sistemas de primer y segundo orden.

Sistema de primer orden

Vamos\(G(s)=\frac{K}{\tau s+1},\;\; u(s)=\frac{1}{s}\); entonces,\(y(s)=\frac{K}{s\left(\tau s+1\right)} =\frac{K}{s} -\frac{K\tau }{\tau s+1}\).

La respuesta en el dominio del tiempo se da como:\(y(t)=K(1-e^{-t/\tau } )\, u(t)\).

Suponiendo condiciones iniciales arbitrarias\(y\left(0\right)=y_0\),, la respuesta escalonada de un sistema de primer orden se da como:

\[y\left(t\right)=y_{\infty }+\left(y_0-y_{\infty }\right)e^{-t/\tau },\ \ t\ge 0\]

Ejemplo\(\PageIndex{1}\)

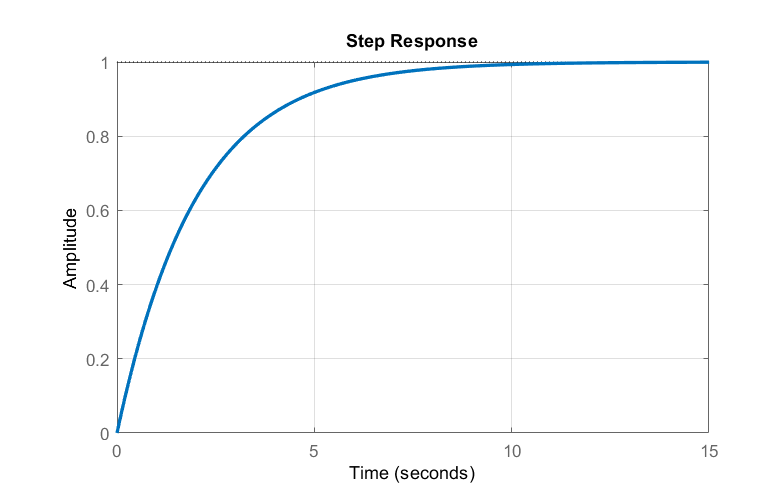
Dejar\(G(s)=\frac{1}{2s+1}\); entonces, la respuesta unidad-paso se obtiene como:\(y(s)=\frac{1}{s\left(2s+1\right)} =\frac{1}{s} -\frac{2}{2s+1}\).

La respuesta en el dominio del tiempo se da como:\(y(t)=(1-e^{-t/2 } )\, u(t)\).

pkg load control
s=tf('s');
Gs=1/(2*s+1);
step(Gs), grid on

Figura\(\PageIndex{1}\): Respuesta escalonada del modelo de motor de CC de primer orden.

Sistema de primer orden con integrador

Vamos\(G(s)=\frac{K}{s\left(\tau s+1\right)}, \;\;u(s)=\frac{1}{s}\); entonces,\(y(s)=\frac{K}{s^{2} \left(\tau s+1\right)}\).

Usando PFE, obtenemos:\(y(s)=K\left(\frac{1}{s^{2} } -\frac{\tau }{s} +\frac{\tau ^{2} }{\tau s+1} \right)\). De ahí,\[g(t)=K\left(t-\tau \left(1-e^{-t/\tau } \right)\right)\, u(t)\] La respuesta paso crece fuera de atados como\(t\to \infty\).

Ejemplo\(\PageIndex{2}\)

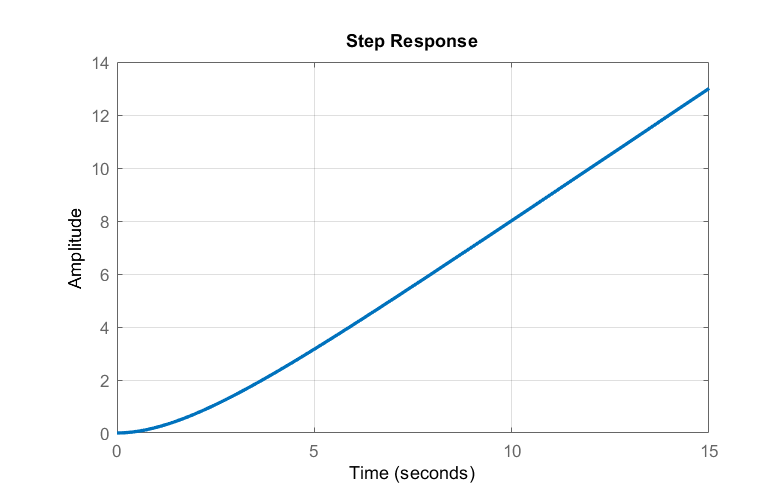
Dejar\(G(s)=\frac{1}{s(2s+1)}\); entonces, la respuesta unidad-paso se calcula como:\(y(s)=\frac{1}{s^2(2s+1)}=\frac{1}{s^2}-\frac{2}{s} +\frac{4}{2s+1}\).

La respuesta en el dominio del tiempo se da como:\(y(t)=(t-2+2e^{-t/2 } )\, u(t)\).

pkg load control
s=tf('s');
Gs=1/s/(2*s+1);
step(Gs), grid on

Figura\(\PageIndex{2}\): Respuesta escalonada de un modelo de segundo orden con un polo en el origen.

Sistema de segundo orden con postes reales

Dejar\(G(s)=\frac{K}{(\tau _{1} s+1)(\tau _{2} s+1)}\),\({\tau }_1>{\tau }_2\); entonces, la respuesta paso se calcula como:\(y(s)=\frac{K}{s(\tau _{1} s+1)(\tau _{2} s+1)} =\frac{A}{s} +\frac{B}{\tau _{1} s+1} +\frac{C}{\tau _{2} s+1}\). Por lo tanto,\[y(t)=(A+Be^{-t/\tau _{1} } +Ce^{-t/\tau _{2} } )u(t)\]

donde\(A=K,B=-\frac{K{\tau }^2_1}{{\tau }_1-{\tau }_2},\ C=\frac{K{\tau }^2_2}{{\tau }_2-{\tau }_1}\).

Ejemplo\(\PageIndex{3}\)

Un pequeño motor de CC tiene los siguientes valores de parámetros:\(R=1\; \Omega ,\; L=10\; {mH},\; J=0.01\; {kg-m}^{2} ,b=0.1\; \frac{N-s}{rad} ,\; k_{t} =k_{b} =0.05\).

La función de transferencia del motor, desde el voltaje de la armadura hasta la velocidad del motor, se aproxima como:\(G\left(s\right)=\frac{500}{\left(s+10\right)\left(s+100\right)}\).

La respuesta escalonada del motor se obtiene como:\(y\left(s\right)=\frac{1}{2s}-\frac{0.556}{s+10}+\frac{0.056}{s+100}\)

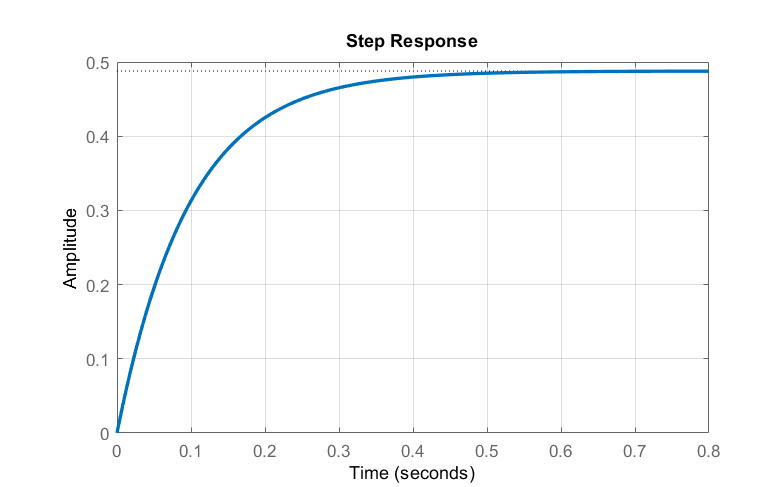
La respuesta en el dominio del tiempo se da como:\(y\left(t\right)=\left(0.5-0.556e^{-10t}+0.056e^{-100t}\right)u(t)\), que se asienta en\(y_{\infty }=0.5\).

Los modos de respuesta natural,\(e^{-10t}\) y\(e^{-100t}\), reflejan las constantes de tiempo eléctricas y mecánicas del motor:\({\tau }_e\cong 0.01s\) y\( {\tau }_m\cong 0.1s\). La constante de tiempo mecánica más lenta domina la respuesta de paso del motor.

pkg load control
s=tf('s');
Gs=500/(s+10)/(s+100);
step(Gs), grid on

Figura\(\PageIndex{3}\): Respuesta escalonada del modelo de motor de CC con polos reales.

Sistema de segundo orden con polos complejos

Vamos\(G(s)=\frac{K}{(s+\sigma )^{2} +\omega _{d}^{2} }\). Entonces, la respuesta unidad-paso se calcula como:\(y(s)=\frac{A}{s} +\frac{Bs+C}{(s+\sigma )^{2} +\omega _{d}^{2} }\),

donde\(A=G(0)=\frac{K}{\sigma ^{2} +\omega _{d}^{2} } ,\, \, B=-A,\, \, C=-2A\sigma\). Por lo tanto,

\[y(t)=\frac{K}{\sigma ^{2} +\omega _{d}^{2} } \left[1-e^{-\sigma t} \left(\cos \; \omega _{d} t+\frac{\sigma }{\omega _{d} } \sin \; \omega _{d} t\right)\right]u(t) \]

En la forma de fase, la respuesta unidad-paso se da como:

\[y(t)=\frac{K}{\sigma ^{2} +\omega _{d}^{2} } \left[1-e^{-\sigma t} \cos \; \left(\omega _{d} t-\phi \right)\right]\, u(t),\, \, \, \phi =\tan ^{-1} \frac{\sigma }{\omega _{d} } \]

Ejemplo\(\PageIndex{4}\)

Un sistema masa-resorte-amortiguador tiene los siguientes valores de parámetros:\(m=1\ kg,\ b=6\frac{Ns}{m},\ k=25\frac{N}{m}\).

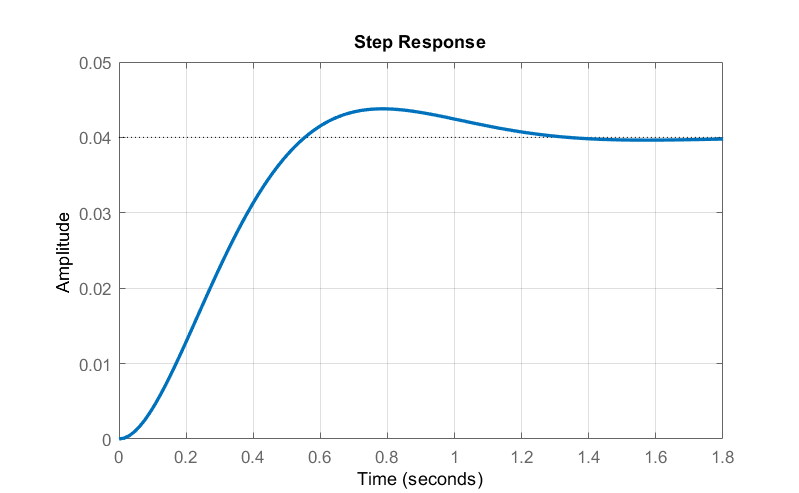
Su función de transferencia se da como:\(G\left(s\right)=\frac{1}{s^2+5s+25}=\frac{1}{{\left(s+3\right)}^2+4^2}\). El sistema cuenta con polos complejos ubicados en:\(s=-3\pm j4\).

La respuesta unidad-paso del sistema se calcula como:\(y\left(s\right)=\frac{1}{25}\left[\frac{1}{s}-\frac{s+6}{{\left(s+3\right)}^2+4^2}\right]\).

Al aplicar la transformada inversa de Laplace, la respuesta en el dominio del tiempo se obtiene como:

\[y\left(t\right)=\frac{1}{25}\left[1-e^{-3t}\left({cos \left(4t\right)\ }+\frac{3}{4}{sin \left(4t\right)\ }\right)\right]u(t)\]

pkg load control
s=tf('s');
Gs=1/(s^2+5*s+25);
step(Gs), grid on

Figura\(\PageIndex{4}\): Respuesta escalonada del modelo masa-resorte-amortiguador con polos complejos.

Sistema con tiempo muerto

El modelo de primer orden más tiempo muerto (FOPDT) de un proceso industrial se da como:\(G(s)=\frac{Ke^{-t_ds} }{\tau s+1}\), donde\(\{K,\tau,t_d\}\) representan la ganancia del proceso, la constante de tiempo y el tiempo muerto.

La respuesta escalonada del modelo FOPDT se calcula como:\(G(s)=\frac{Ke^{-t_ds} }{s(\tau s+1)}\), que se tradujo en una respuesta en el dominio del tiempo como:\(g(t)=(1-e^{-(t-t_d)/\tau})u(t-t_d)\).

Un modelo de proceso aproximado, obtenido mediante la aproximación de Pade, se da como:\(G(s)=\frac{K(1-t_ds/2)}{(1+t_ds/2)(\tau s+1)}\). Este modelo se califica como fase no mínima debido a la fase adicional aportada por el cero del medio plano derecho (RHP).

La respuesta unidad-paso del modelo aproximado se calcula como:\(y(s)=\frac{K(1-t_ds/2)}{s(1+t_ds/2)(\tau s+1)}\).

Ejemplo\(\PageIndex{5}\)

El modelo FOPDT de un biorreactor de tanque agitado se da como:\(G(s)=\frac{20e^{-s} }{0.5s+1}\).

La respuesta escalonada del sistema se calcula como:\(y(s)=\frac{20e^{-s} }{s\left(0.5s+1\right)} \).

La respuesta en el dominio del tiempo se obtiene como:\(y(t)=20\left(1-e^{-2(t-1)} \right)\, u(t-1)\).

Usando una aproximación de Pade de primer orden, se obtiene un modelo de proceso aproximado como:\(G_{a} (s)=\frac{20\left(1-0.5s\right)}{\left(0.5s+1\right)^{2} }\).

La respuesta escalonada del modelo aproximado se calcula como:\(y(s)=\frac{20\left(1-0.5s\right)}{s\left(0.5s+1\right)^{2} } \),\(y(t)=20\left(1-(1-4t)e^{-2t} \right)\, u(t)\).

Las dos respuestas se comparan a continuación (Figura 2.4.5). La respuesta escalonada para el modelo FOPDT comienza después del retraso designado. La respuesta escalonada para la aproximación de Pade comienza con un subbrote debido a la presencia de RHP cero.

pkg load control
s=tf('s');
Gs=20/(.5*s+1);
t=0:.01:5;
u=ones(size(t));
u(1:100)=0;
lsim(Gs,u,t), grid on
hold
Gsa=20*(1-.5*s)/(1+.5*s)^2;
%step(Gsa)
lsim(Gsa,ones(size(t)),t,'r')
legend('sys with deadtime','pade approximation')

Figura\(\PageIndex{5}\): Respuesta escalonada de un modelo de proceso industrial con tiempo muerto.

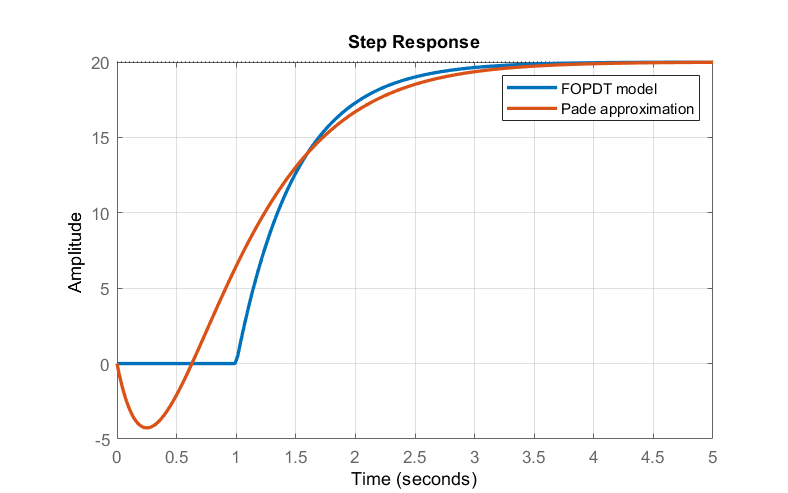
Hacemos las siguientes observaciones con base en la figura:

1. La respuesta escalonada del proceso con tiempo muerto comienza después de 1 s de retraso (como se esperaba).
2. La respuesta escalonada de la aproximación del retraso de Pade tiene un subimpulso. Este comportamiento es característico de los modelos de función de transferencia con ceros ubicados en el plano de la mitad derecha.