7.3: Respuesta del sistema de datos muestreados

La respuesta de un sistema de datos muestreados,\(G\left(z\right)\), a una secuencia de entrada,\(u\left(k\right)\), es la secuencia de salida,\(y(k)\). En el\(z\) dominio -la respuesta del sistema se da como:\(y\left(z\right)=G\left(z\right)u(z)\).

Alternativamente, podemos usar la transformada z inversa para obtener una descripción de entrada-salida en forma de una ecuación de diferencia que se puede resolver por iteración.

7.3.1 Representación de la ecuación de diferencia

Que\(G\left(z\right)=\frac{n\left(z\right)}{d\left(z\right)},\) donde\(n\left(z\right)\) y\(d\left(z\right)\) son\(m\) polinomios de orden\(n\) th y th orden, dados como:

\[n\left(z\right)=\sum^m_{i=0}{b_iz^{m-i}},\ \ d\left(z\right)=z^n+\sum^n_{i=1}{a_iz^{n-i}}.\]

Entonces\(d\left(z\right)y\left(z\right)=n\left(z\right)u\left(z\right)\). Al aplicar la\(z\) transformada inversa, obtenemos una ecuación de diferencia, descrita como:

\[y\left(k+n\right)+\sum^n_{i=1}{a_iy\left(k+n-i\right)}+\sum^m_{i=0}{b_iu\left(k+m-i\right)}\]

Como el sistema es lineal e invariable en el tiempo, aplicamos un cambio de tiempo y reorganizamos la ecuación de diferencia en y actualizamos la regla:

\[y\left(k\right)=-\sum^n_{i=1}{a_iy\left(k-i\right)}+\sum^m_{i=0}{b_iu\left(k-i\right)}\]

La regla anterior se puede programar en una computadora para resolver la respuesta del sistema de datos muestreados a una secuencia de entrada,\(u\left(k\right)\), descrita como: as\(u\left(k\right)={\left.u\left(t\right)\right|}_{t=kT}\).

Ejemplo\(\PageIndex{1}\)

Let\(G(z)=\frac{y(z)}{u(z)} =\frac{0.181}{z-0.819}\); entonces, el sistema de datos muestreados se describe mediante la siguiente relación entrada-salida:

\[y\left(k\right)=0.819y\left(k-1\right)+0.181u\left(k-1\right)\]

 

Ejemplo\(\PageIndex{2}\)

Let\(G(z)=\frac{0.0187(z+0.936)}{(z-1)(z-0.819)}\); entonces, el sistema de datos muestreados se describe mediante la siguiente relación entrada-salida:

\[y\left(k\right)=1.819y\left(k-1\right)-0.819y\left(k-2\right)+0.0187u\left(k-1\right)+0.0175u(k-2)\]

Respuesta de pulso de unidad

La respuesta unidad-pulso de un modelo de sistema de datos muestreados\(G(z)\),, es su respuesta a un pulso unitario\(r(k)=\delta (k)\).

Utilizando\(r\left(z\right)=1\), la respuesta unidad-pulso se calcula como:\(g\left(kT\right)=z^{-1}\left[G(z)\right]\), con un tiempo de muestreo implícito\(T=1s\).

La respuesta unidad-pulso para el tiempo de muestra,\(T\), se obtiene asumiendo\(\delta \left(z\right)=\frac{1}{T}\), por lo tanto\(g\left(kT\right)=\frac{1}{T}z^{-1}\left[G(z)\right]\).

Alternativamente, dada la descripción de entrada-salida, la respuesta de pulso unitario se puede calcular por iteración.

La respuesta unidad-pulso comprende los modos de respuesta natural\(G\left(z\right)=n(z)/d\left(z\right)\). Estos modos dependen de las raíces de\(d\left(z\right)\), y se caracterizan de la siguiente manera:

Raíces reales. Supongamos que\(d\left(z\right)\) tiene raíces reales y distintas:\(z_{i} ,\; i=1,\ldots ,n,\) entonces, los modos de respuesta naturales se dan como:\(\phi _{i} (k)=(z_{i} )^{k}\). Estos modos se extinguen con el tiempo si\(|z_{i} |<1.\)

Raíces Complejas. Supongamos que\(d\left(z\right)\) tiene raíces complejas de la forma:\(re^{\pm j\theta }\); entonces, sus modos de respuesta naturales se dan como:\(\phi _{i} (k)=\{ r^{k} \; \cos k\theta ,\; r^{k} \; \sin k\theta \}\). Estos modos de manera similar se extinguen con el tiempo si\(|r|<1\).

Ejemplo\(\PageIndex{3}\)

Dejar\(G(s)=\frac{1}{s+1}\); utilizar\(T=0.2\rm s\) para obtener:\(G(z)=\frac{0.181}{z-0.819}\). El sistema de datos muestreados se describe mediante la siguiente relación entrada-salida:\(y\left(k\right)=0.819y\left(k-1\right)+0.181u\left(k-1\right).\)

Como\(T=0.2s\), let\(\delta \left(k\right)=\{5,\ 0,\ 0,\dots \}\); entonces, asumiendo cero condiciones iniciales, la respuesta de pulso unitario se obtiene como:

\[y\left(k\right)=\left\{0,0.906,\ 0.742,\ 0.608,\ 0.497,0.407,\ 0.333,\ \dots \right\}\]

A modo de comparación, la respuesta de impulso del sistema analógico se obtiene como:\(g\left(t\right)=e^{-t}u(t)\).

Las respuestas impulsivas de sistemas continuos y discretos se comparan en la Figura 7.3.1.

Figura\(\PageIndex{1}\): Respuestas de pulso unitario de sistemas de tiempo continuo y datos muestreados para el Ejemplo 7.3.3.

Ejemplo\(\PageIndex{4}\)

Dejar\(G(s)=\frac{1}{s(s+1)}\); utilizar\(T=0.2\rm s\) para obtener:\(G(z)=\frac{0.0187(z+0.936)}{(z-1)(z-0.819)}\). El sistema de datos muestreados se describe mediante la siguiente relación entrada-salida:

\[y\left(k\right)=1.819y\left(k-1\right)-0.819y\left(k-2\right)+0.0187u\left(k-1\right)+0.0175u(k-2).\]

Suponiendo\(u\left(k\right)=\{5,0,0,\dots \}\), y cero condiciones iniciales, la respuesta de pulso unitario se obtiene como:

\[y\left(k\right)=\left\{0,0.0937,\ 0.258,\ 0.392,\ 0.502,0.593,\ 0.667,\ \dots \right\}\]

A modo de comparación, la respuesta de impulso del sistema analógico original se obtiene como:\(g\left(t\right)=(1-e^{-t})u(t)\).

Las respuestas impulsivas de sistemas continuos y discretos se comparan en la Figura 7.3.2. Observamos que la presencia de integrador en la función de transferencia provoca que la respuesta de impulso se aproxime asintóticamente a la unidad en el estado estacionario.

Figura\(\PageIndex{2}\): Respuestas de pulso unitario de sistemas de tiempo continuo y datos muestreados para el Ejemplo 7.3.4.

En MATLAB Control Systems Toolbox, el comando 'impulse' se puede utilizar para obtener o trazar la respuesta unidad-pulso de un sistema de datos muestreados.

Respuesta de paso de unidad

La respuesta unidad-paso de un modelo de sistema de datos muestreados\(G\left(z\right)\),, es su respuesta a la secuencia unidad-paso:\(r\{ kT\} =\{ 1,1,1\ldots \}\);\(r(z)=\frac{1}{1-z^{-1} }\). En el\(z\) dominio -se obtiene la respuesta unidad-paso como:\(y(z)=\frac{G(z)}{1-z^{-1} }\).

Alternativamente, usando la descripción del sistema de entrada-salida, la respuesta unidad-paso se puede obtener por iteración.

Ejemplo\(\PageIndex{5}\)

Dejar\(G(s)=\frac{1}{s+1}\); utilizar\(T=0.2\rm s\) para obtener:\(G(z)=\frac{0.181}{z-0.819}\). La respuesta unidad-paso se calcula como:\(y(z)=\frac{0.181z}{\left(z-1\right)\left(z-0.819\right)}\).

Utilizamos PFE de\(y(z)/z\) para obtener:\(y(z)=\left(\frac{z}{z-1} -\frac{z}{z-0.819} \right).\) Usando la\(z\) transformada inversa, la secuencia de respuesta paso se obtiene como:\(y(kT)=1-(0.819)^{k} ,\; \; k=0,1,\ldots\)

Alternativamente, usamos la descripción del sistema de entrada-salida con cero condiciones iniciales:\(y\left(k\right)=0.819y\left(k-1\right)+0.181u\left(k-1\right).\) La secuencia de unidad-paso resultante se da como:\(y\left(k\right)=\left\{0,\ 0.181,\ 0.329,\ 0.451,\ 0.55,\dots \right\}\).

A modo de comparación, la respuesta unidad-paso del sistema de tiempo continuo se da como:\(y(t)=1-e^{-t} ,\; \; t>0.\) Las respuestas escalonadas de los sistemas continuo y discreto se trazan al lado (Figura 7.3.3).

Figura\(\PageIndex{3}\): Respuestas de paso unitario de sistemas de tiempo continuo y datos muestreados para el Ejemplo 7.3.5.

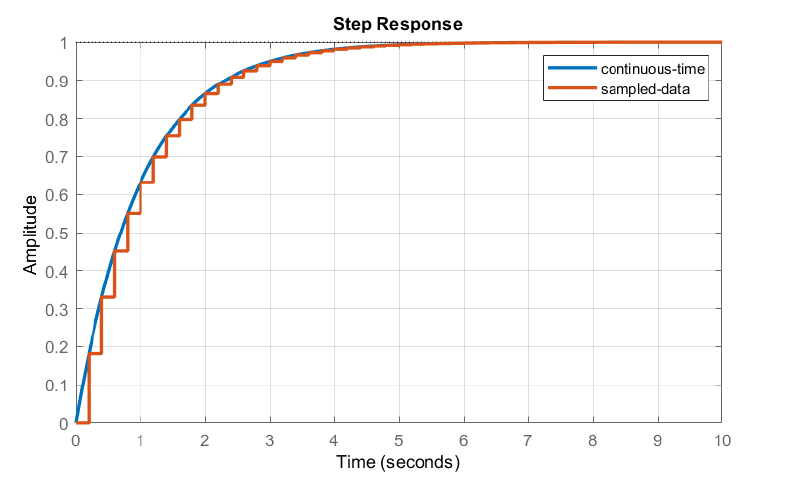
Ejemplo\(\PageIndex{6}\)

Dejar\(G(s)=\frac{1}{s(s+1)}\); utilizar\(T=0.2\rm s\) para obtener:\(G(z)=\frac{0.0187z+0.0175}{z^{2} -1.819z+0.819}\). Usando la relación de dominio de tiempo (Ejemplo 6.8), la respuesta unidad-paso se da como:\(\{ 0,\; \; 0.0187,\; 0.0702,\; 0.149,\, 0.249,\, 0.368,\, 0.501,0.647,0.802,0.965,\ldots \}\)

Analíticamente, let\(r(z)=\frac{z}{z-1}\) (unidad-paso); entonces, la salida del sistema se da como:\(y(z)=\frac{z(0.0187z+0.0175)}{(z-1)(z^{2} -1.819z+0.819)}\). Al usar la división larga, podemos expresar el cociente como:

\[y(z)=0.0187z^{-1} +0.0703z^{-2} +0.149z^{-3} +0.249z^{-4} +0.501z^{-5} +\ldots\]

La secuencia de salida resultante coincide con la obtenida por iteración.

Para comparación, la respuesta de paso del sistema de tiempo continuo se da como:\(y(t)=(t-1+e^{-t} )u(t).\)

Las respuestas escalonadas de los sistemas continuos y discretos se trazan al lado (Figura 7.3.4).

Figura\(\PageIndex{4}\): Respuestas de paso unitario de sistemas de tiempo continuo y datos muestreados para el Ejemplo 7.3.6.

En MATLAB Control Systems Toolbox, el comando 'step' se puede utilizar para obtener o trazar la respuesta unidad-paso de un sistema de datos muestreados.

Respuesta a las entradas arbitrarias

Dada la respuesta unidad-pulso del sistema, su respuesta a una secuencia de entrada arbitraria se obtiene por convolución. Por consiguiente, se dé la secuencia de respuesta de pulso unitario como:

\[\left\{g\left(k\right)\right\}=\{g\left(1\right),\ g\left(2\right),\ \dots \}\]

Luego, usando una secuencia de entrada arbitraria:\(\left\{u\left(k\right)\right\}=\{u\left(1\right),\ u\left(2\right),\ \dots \}\), la secuencia de salida viene dada por la suma de convolución:

\[y\left(k\right)=g\left(k\right)*u\left(k\right)=\sum^{\infty }_{i=0}{g\left(k-i\right)u\left(i\right)}\]

Como ejemplo, obtenemos la salida para una entrada sinusoidal a continuación.

Ejemplo\(\PageIndex{7}\)

Vamos\(G(z)=\frac{0.368z+0.264}{(z-1)(z-0.368)}\); asumimos una secuencia de entrada sinusoidal,\(u\left(kT\right)={sin \left(\pi kT\right)\ }\). Entonces, se calcula la respuesta de salida utilizando la suma de convolución que se muestra (Figura 7.3.5).

Figura\(\PageIndex{5}\): Respuesta sinusoidal de un sistema de datos muestreados de segundo orden precedido por un ZOH.