4.4: Relación con las normas matriciales
- Page ID
- 85721
La descomposición del valor singular se puede utilizar para calcular la norma 2 inducida de una matriz A.
Teorema 4.2
\ [\ begin {alineado}
\ |A\ |_ {2} &\ triangleq\ sup _ {x\ neq 0}\ frac {\ |A x\ |_ {2}} {\ |x\ |_ {2}}\\
&=\ sigma_ {1}\\
&=\ sigma_ {\ max} (A)
\ end {alineado}\\ tag {21}\]
que nos dice que la amplificación máxima viene dada por el valor singular máximo.
- Prueba
-
\ [\ begin {alineado}
\ sup _ {x\ neq 0}\ frac {\ |A x\ |_ {2}} {\ |x\ |_ {2}} &=\ sup _ {x\ neq 0}\ frac {\ izquierda\ |U\ Sigma V^ {\ prime} x\ derecha\ |_ {2}} {\ |x\ |_ {2}}\
&=\ sup _ {x\ neq 0}\ frac {\ izquierda\ |\ Sigma V^ {\ prime} x\ derecha\ |_ {2}} {\ |x\ |_ {2}}\\
&=\ sup _ {y \ neq 0}\ frac {\ |\ Sigma y\ |_ {2}} {\ |V y\ |_ {2}}\\
&=\ sup _ {y\ neq 0}\ frac {\ izquierda (\ suma_ {i=1} ^ {r}\ sigma_ {i} ^ {2}\ izquierda|y_ {i}\ derecha|^ {2}\ derecha) ^ {\ frac {1} {2}}} {\ izquierda (\ suma_ {i=1} ^ {r}\ izquierda|y_ {i}\ derecha|^ {2}\ derecha) ^ {\ frac {1} {2}}}\\
&\ leq\ sigma_ {1}
\ end { alineado}\ nonumber\]Para\ (y=\ left [\ begin {array} {lll}
1 & 0 &\ cdots & 0
\ end {array}\ right] ^ {T},\ |\ Sigma y\ |_ {2} =\ sigma_ {1}\), y se alcanza la suprema. (Observe que este correponds a\(x = v_{1}\). De ahí que,\(Av_{1}=\sigma_{1}u_{1}.\)
Otra aplicación de la descomposición del valor singular es en el cálculo de la amplificación mínima que una matriz de rango completo ejerce sobre elementos con 2-norma igual a 1.
Teorema 4.3
Dado\(A \in C^{m \times n}\), supongamos\(rank(A) = n\). Entonces
\[\min _{\|x\|_{2}=1}\|A x\|_{2}=\sigma_{n}(A)\ \tag{4.22}\]
Tenga en cuenta que si\(rank(A) < n\), entonces hay\(x\) tal que el mínimo es cero (reescribir\(A\) en términos de su SVD para ver esto).
- Prueba
-
Para cualquier\(\|x\|_{2}=1\),
\ [\ begin {alineado}
\ |A x\ |_ {2} &=\ izquierda\ |U\ Sigma V^ {\ prime} x\ derecha\ |_ {2}\\
&=\ izquierda\ |\ Sigma V^ {\ prime} x\ derecha\ |_ {2}\ quad\ text {(invariante bajo multiplicación por matrices unitarias)}\\
&=\ |\ Sigma\ _ {2}
\ fin {alineado}\ nonumber\]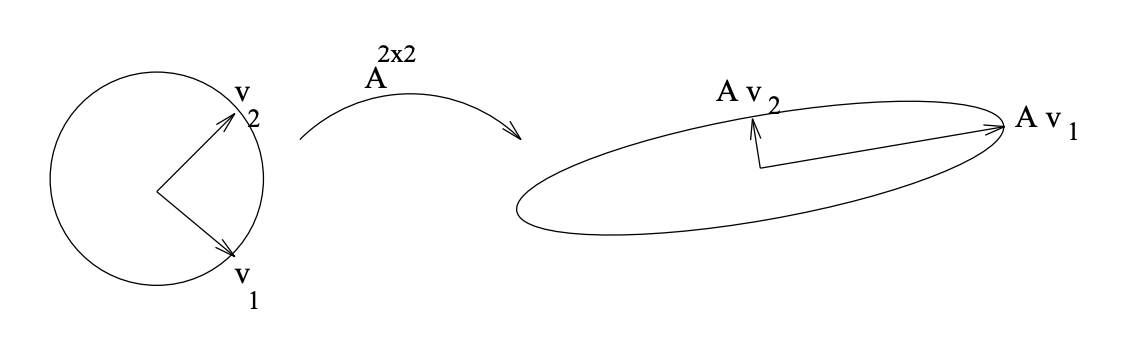
Figura\(\PageIndex{1}\): Representación gráfica del mapeo que involucra A^ {2\ times 2}\). Tenga en cuenta eso\(Av_{1} = \sigma_{1} u_{1}\) y eso\(Av_{2} = \sigma_{2} u_{2}\).
para\(y = V^{\prime}x\). Ahora
\ [\ begin {alineado}
\ |\ Sigma y\ |_ {2} &=\ izquierda (\ suma_ {i=1} ^ {n}\ izquierda|\ sigma_ {i} y_ {i}\ derecha|^ {2}\ derecha) ^ {\ frac {1} {2}}\
&\ geq\ sigma_ {n}
\ end {alineado}\ nonumber\]Tenga en cuenta que se alcanza el mínimo para\ (y=\ left [\ begin {array} {llll}
0 &\ cdots & 0 &1
\ end {array}\ right] ^ {T}\); así la prueba está completa.
La norma Frobenius también puede expresarse de manera bastante simple en términos de los valores singulares. Te dejamos para verificar que
\ [\ begin {alineado}
\ |A\ |_ {F} &\ triangleq\ izquierda (\ suma_ {j=1} ^ {n}\ suma_ {i=1} ^ {m}\ izquierda|a_ {i j}\ derecha|^ {2}\ derecha) ^ {\ frac {1} {2}}\
&=\ izquierda (\ nombreoperador {traza}\ izquierda (A^ {\ prime} A\ derecha)\ derecha) ^ {\ frac {1} {2}}\\
&=\ izquierda (\ sum_ {i=1} ^ {r}\ sigma_ {i} ^ {2}\ derecha) ^ {\ frac {1} { 2}}
\ final {alineado}\\ etiqueta {4.23}\]
Ejemplo 4.4 Desigualdad matricial
Decimos\(A \leq B\), dos matrices cuadradas, si
\[x^{\prime} A x \leq x^{\prime} B x \quad \text { for all } x \neq 0\nonumber\]
De ello se deduce que para cualquier matriz A, no necesariamente cuadrada,
\[\|A\|_{2} \leq \gamma \leftrightarrow A^{\prime} A \leq \gamma^{2} I.\nonumber\]


