5.5: Acondicionamiento de la Inversión Matricial

Ahora estamos en condiciones de abordar algunos de los temas que surgieron en el Ejemplo 1 de la Conferencia 4, respecto a la sensibilidad de lo inverso\(A^{-1}\) y de la solución\(x = A^{-1}b\) a las perturbaciones en\(A\) (y/o\(b\), para el caso). Primero consideramos el caso donde\(A\) es invertible, y examinar la sensibilidad de\(A^{-1}\). Tomando diferenciales en la ecuación definitoria\(A^{-1}A = I\), encontramos

\[d\left(A^{-1}\right) A+A^{-1} d A=0 \ \tag{5.23}\]

donde el orden de los términos en cada mitad de la suma es importante, claro. (En lugar de trabajar con diferenciales, podríamos trabajar de manera equivalente con perturbaciones de la forma\(A+\epsilon P\), etc., donde\(\epsilon\) es muy pequeño, pero esto realmente equivale a lo mismo). Reordenando la expresión anterior, encontramos

\[d\left(A^{-1}\right) = A^{-1} d A A^{-1} \ \tag{5.24}\]

Tomando normas, el resultado es

\[\left\|d\left(A^{-1}\right)\right\| \leq\left\|A^{-1}\right\|^{2}\|d A\| \ \tag{5.25}\]

o equivalentemente

\[\frac{\left\|d\left(A^{-1}\right)\right\|}{\left\|A^{-1}\right\|} \leq\|A\|\left\|A^{-1}\right\| \frac{\|d A\|}{\|A\|} \ \tag{5.26}\]

Esta derivación se mantiene para cualquier norma submultiplicativa. El producto\(\|A\|\left\|A^{-1}\right\|\) se llama el número de condición de\(A\) con respecto a la inversión (o simplemente el número de condición de\(A\)) y se denota por\(K(A)\):

\[K(A) = \|A\|\left\|A^{-1}\right\| \ \tag{5.27}\]

Cuando deseamos especificar qué norma se está utilizando, se adjunta un subíndice\(K(A)\). Nuestros resultados anteriores sobre la SVD muestran, por ejemplo, que

\[K_{2}(A)=\sigma_{\max } / \sigma_{\min } \ \tag{5.28}\]

El número de condición en esta norma 2 nos dice cuán delgado\(\|x\|_{2}=1\) es el elipsoide\(Ax\) para - ver Figura 5.1. En lo que sigue, nos centraremos en el número de condición de 2 normas (pero omitiremos el subíndice a menos que sea esencial).

Algunas propiedades del número de condición de 2 normas (todas las cuales son fáciles de mostrar y algunas de las cuales se extienden al número de condición en otras normas) son

• \(K(A) \geq 1;\)
• \(K(A) = K(A^{-1});\)
• \(K(AB) \leq K(A) K(B);\)
• Dado\(U^{\prime}U = I\),\(K(UA) = K(A)\).

La importancia de (5.26) es que el límite se puede lograr realmente para alguna elección de la perturbación\(dA\) y de la norma matricial, por lo que la situación puede llegar a ser tan mala como lo permita el límite: el cambio fraccionario en el inverso puede ser\(K(A)\) veces tan grande como el cambio fraccionario en el original . En el caso de las 2 normas, una perturbación particular que alcanza el

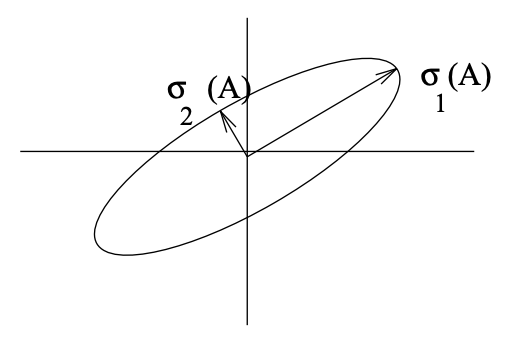
Figura\(\PageIndex{1}\): Representación de cómo A (una\(2 \times 2\) matriz real) mapea el círculo unitario. El eje mayor de la elipse corresponde al mayor valor singular, el eje menor al más pequeño.

se puede derivar\(\Delta\) del Teorema 5.1, simplemente reemplazando\(-\sigma_{n}\) en\(\Delta\) por una perturbación diferencial:

\[d A=-d \sigma u_{n} v_{n}^{\prime} \ \tag{5.29}\]

Hemos establecido que un número de condición grande corresponde a una matriz cuya inversa es muy sensible a perturbaciones relativamente pequeñas en la matriz. Tal matriz se llama mal condicionada o mal condicionada con respecto a la inversión. Una matriz perfectamente acondicionada es aquella cuyo número de condición toma el valor mínimo posible, a saber, 1.

Un número de condición alta también indica que una matriz está cerca de perder rango, en el siguiente sentido: Hay una perturbación\(\Delta\) de norma pequeña (\(=\sigma_{min}\)) relativa a\(\|A\|\left(=\sigma_{\max }\right)\) tal que\(A + \Delta\) tiene rango menor que\(A\). Esto se desprende de nuestro resultado de perturbación aditiva en el Teorema 5.1. Esta interpretación también se extiende a matrices no cuadradas. Denominaremos la relación en (5.28) el número de condición de\(A\) incluso cuando no\(A\) es cuadrado, y pensaremos en ello como una medida de cercanía a una pérdida de rango.

Pasando ahora a la sensibilidad de la solución\(x = A^{-1}b\) de un sistema lineal de ecuaciones en la forma\(Ax = b\), podemos proceder de manera similar. Tomando diferenciales, encontramos que

\[d x=-A^{-1} d A A^{-1} b+A^{-1} d b=-A^{-1} d A x+A^{-1} b \ \tag{5.30}\]

Tomando normas y luego rinde

\[\|d x\| \leq\left\|A^{-1}\right\|\|d A\|\|x\|+\left\|A^{-1}\right\|\|d b\| \ \tag{5.31}\]

Dividiendo ambos lados de esto por\(\|x\|\), y usando el hecho de que\(\|x\| \geq (\|b\|/\|A\|)\), obtenemos

\[\frac{\|d x\|}{\|x\|} \leq K(A)\left(\frac{\|d A\|}{\|A\|}+\frac{\|d b\|}{\|b\|}\right) \ \tag{5.32}\]

Podemos acercarnos a alcanzar este límite si, por ejemplo,\(b\) pasa a ser casi colineal con la columna de\(U\) en la SVD de la\(A\) que se asocia\(\sigma_{min}\), y si se producen perturbaciones apropiadas. Una vez más, por lo tanto, el cambio fraccionario en la respuesta puede ser cercano a\(K(A)\) tiempos tan grandes como los cambios fraccionarios en las matrices dadas.

Ejemplo 5.2

Para la matriz A dada en el Ejemplo 1 de la Conferencia 4, la SVD es

\ [A=\ left (\ begin {array} {cc}
100 & 100\\
100.2 & 100
\ end {array}\ right) =\ left (\ begin {array} {cc}
.7068 & .7075\\
.7075 & .-7068
\ end {array}\ right)\ left (\ begin {array} {cc} {cc}
200.1 & 0\\
0 & 0.1
\ end {array}\ derecha)\ left (\ begin {array} {cc}
.7075 & .7068\
-.7068 & .7075
\ end {array}\ right)\ tag {5.33}\]

El número de condición de se ve que\(A\) es 2001, lo que explica el aumento de 1000 veces del error en la inversa para la perturbación que usamos en ese ejemplo. La perturbación\(\Delta\) de la norma 2 más pequeña que hace\(A + \Delta\) que se vuelva singular es

\ [\ Delta=\ left (\ begin {array} {cc}
.7068 & .7075\\
.7075 & .-7068
\ end {array}\ right)\ left (\ begin {array} {cc}
0 & 0\\
0 & -0.1
\ end {array}\ right)\ left (\ begin {array} {cc}
.7075 & .7068\\
-.7068 & .7075
\ end {array}\ derecha)\ nonumber\]

cuya norma es 0.1. Llevar a cabo la multiplicación da

\ [\ Delta\ approx\ left (\ begin {array} {cc}
.05 & -.05\\
-.05 & .05
\ end {array}\ right)\ nonumber\]

Con\(b = [1 - 1]^{T}\), vimos gran sensibilidad de la solución\(x\) a las perturbaciones en\(A\). Tenga en cuenta que esto\(b\) es de hecho casi colineal con la segunda columna de\(U\). Si, por otro lado, tuviéramos\ (b=\ left [\ begin {array} {ll}
1 & 1
\ end {array}\ right]\), que está más estrechamente alineado con la primera columna de\(U\), entonces la solución difícilmente se habría visto afectada por la perturbación en\(A\) - una afirmación que te dejamos verificar.

Por lo tanto,\(K(A)\) sirve como un límite en el factor de aumento que relaciona los cambios fraccionarios en\(A\) o\(b\) con los cambios fraccionarios en nuestra solución\(x\).

Acondicionamiento de la estimación de mínimos cuadrados

Nuestro objetivo en el problema de estimación de errores mínimos cuadrados fue encontrar el valor\(\widehat{x}\) de\(x\) que minimiza\(\|y-A x\|_{2}^{2}\), bajo el supuesto de que\(A\) tiene rango de columna completa. Un análisis detallado del condicionamiento de este caso está fuera de nuestro alcance (ver Cálculo Matrix de Golub y Van Loan, citado anteriormente, para un tratamiento detallado). Lo haremos aquí con una declaración del resultado principal en el caso de que el residuo fraccional sea mucho menor que 1, i.e.

\[\frac{\|y-A \widehat{x}\|_{2}}{\|y\|_{2}} \ll 1 \ \tag{5.34}\]

Este caso de baja residual es ciertamente de interés en la práctica, asumiendo que se está ajustando un modelo razonablemente bueno a los datos. En este caso, se puede demostrar que el cambio fraccionario\(\|d \widehat{x}\|_{2} /\|\widehat{x}\|_{2}\) en la solución\(\widehat{x}\) puede aproximarse a\(K(A)\) veces la suma de los cambios fraccionarios en\(A\) y\(y\), donde\(K(A)=\sigma_{\max }(A) / \sigma_{\min }(A)\). A la luz de nuestros resultados anteriores para el caso de invertible\(A\), este resultado quizás no sea sorprendente.

Ante este resultado, es fácil explicar por qué resolver las ecuaciones normales

\[\left(A^{\prime} A\right) \widehat{x}=A^{\prime} y\nonumber\]

para determinar\(\widehat{x}\) es numéricamente poco atractivo (en el caso de baja residual). La inversión numérica de\(A^{\prime}A\) se rige por el número de condición de\(A^{\prime}A\), y este es el cuadrado del número de condición de\(A\):

\[K\left(A^{\prime} A\right)=K^{2}\tag{A}\]

Debe confirmarlo usando el SVD de\(A\). El proceso de resolver directamente las ecuaciones normales introducirá así errores que no son intrínsecos al problema de menor error cuadrado, ya que este problema se rige por el número de condición\(K(A)\), de acuerdo con el resultado citado anteriormente. Afortunadamente, existen otros algoritmos para la computación\(\widehat{x}\) que se rigen por el número de condición\(K(A)\) en lugar del cuadrado de este (y Matlab usa uno de esos algoritmos para calcular\(\widehat{x}\) cuando invoca su comando de solución de mínimos cuadrados).