20.9: Ejercicios

Ejercicio\(\PageIndex{20.1}\)

Considerar una planta descrita por la matriz de funciones de transferencia

\ [P_ {\ alpha} (s) =\ left (\ begin {array} {cc}
\ frac {\ alpha} {s-1} &\ frac {1} {s-1} {s-1}
\\ frac {2 s-1} {s (s-1)} &\ frac {1} {s-1}
\ end {array}\ derecha)\ nonumber\]

donde\(\alpha\) es un parámetro real pero incierto, confinado al rango [0:5, 1:5]. Deseamos diseñar un compensador de retroalimentación\(K(s)\) para una estabilidad robusta de un servo loop estándar alrededor de la planta.

a) Nos gustaría encontrar un valor de\(\alpha\), digamos, y un escalar\(\tilde{\alpha}\), estable, racional adecuado de\(W(s)\) tal manera que el conjunto de plantas posibles\(P_{\alpha}(s)\) quede contenido dentro del “conjunto de incertidumbre”

\[P_{\tilde{\alpha}}(s)[I+W(s) \Delta(s)]\nonumber\]

donde se\(\Delta(s)\) extiende sobre el conjunto de matrices racionales estables y adecuadas con\(\|\Delta\|_{\infty} \leq 1\). Prueba y encuentra (¡no hay garantías de que esto es posible!) un adecuado\(\tilde{\alpha}\) y\(W(s)\), quizás teniendo en cuenta que lo que realmente queremos hacer es garantizar

\[\sigma_{\max }\left\{P_{\tilde{\alpha}}^{-1}(j \omega)\left[P_{\alpha}(j \omega)-P_{\tilde{\alpha}}(j \omega)\right]\right\} \leq|W(j \omega)|\nonumber\]

Qué elección específica de\(\Delta(s)\) rinde la planta\(P_{1}(s)\) (es decir, la planta con

b) Repetir la parte (a), pero ahora trabajando con el conjunto de incertidumbre

\[P_{\tilde{\alpha}}(s)\left[I+W_{1}(s) \Delta(s) W_{2}(s)\right]\nonumber\]

donde\(W_{1}(s)\) y\(W_{2}(s)\) son vectores de columna y fila respectivamente, y\(\Delta(s)\) es escalar. Trazar el límite superior en

\[\sigma_{\max }\left\{P_{\tilde{\alpha}}^{-1}(j \omega)\left[P_{\alpha}(j \omega)-P_{\tilde{\alpha}}(j \omega)\right]\right\}\nonumber\]

que obtengas en este caso.

c) Para cada uno de los casos anteriores, anotar una condición suficiente para una estabilidad robusta del sistema de bucle cerrado, expresada en términos de una condición norma que involucre la función de sensibilidad complementaria nominal\(T=\left(I+K P_{\tilde{\alpha}}\right)^{-1} K P_{\tilde{\alpha}}\)\(W-\) y/o, en la parte (b),\(W_{1}\) y\(W_{2}\).

Ejercicio\(\PageIndex{20.2}\)

Resulta que el teorema de pequeña ganancia también es válido para sistemas no lineales. Considere una configuración de retroalimentación con un sistema estable\(M\) en el bucle directo y una perturbación estable y desconocida en el bucle de retroalimentación. Supongamos que la configuración está bien planteada. Verifique que el sistema de bucle cerrado sea estable si\(\|M\|\|\Delta\|<1\). Aquí la norma es la ganancia del sistema sobre cualquier norma p. (Este resultado también es cierto para los sistemas DT y CT; la misma prueba se mantiene).

Ejercicio\(\PageIndex{20.3}\)

El diseño de un controlador debe tomar en consideración los efectos de cuantificación. Supongamos que la única variable en el bucle cerrado que está sujeta a cuantificación es la salida de la planta. Se proponen dos esquemas muy simples:

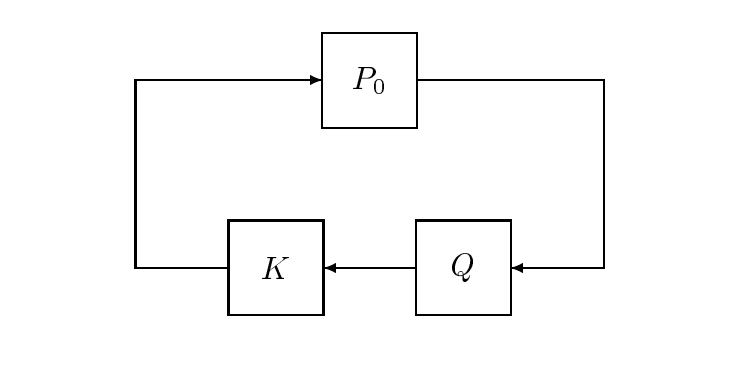
Figura 20.8: Cuantización en el Bucle Cerrado

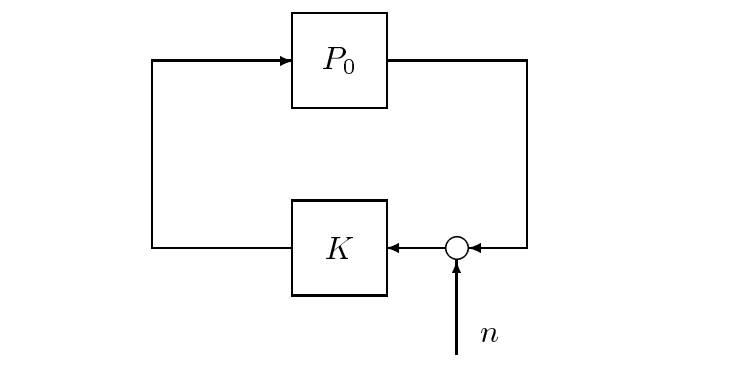
Figura 20.9: Cuantización modelada como ruido acotado

1. Supongamos que la salida se pasa a través de un operador de cuantificación\(Q\) definido como:

\[Q(x)=a\left\lfloor\frac{|x|}{.5+a}\right\rfloor \operatorname{sgn}(x), \quad a>0\nonumber\]

donde\([r]\) denota el entero más grande menor que\(r\). La salida de este operador alimenta al controlador como en la Figura 20.8. Derivar una condición suficiente que garantice la estabilidad ante la presencia de\(Q\).

2. Supongamos que la entrada del controlador está corrompida con una señal desconocida pero acotada, con un pequeño límite como en la Figura 20.9. Argumentan que el controlador debe diseñarse para que no amplifique esta perturbación en su entrada.

Compara los dos esquemas, es decir, ¿arrojan el mismo resultado? ¿Hay alguna diferencia?