5.1: Cuatro preguntas
- Page ID
- 86365
La segunda ley de Newton, comúnmente escrita como\(F=m a\), es una de las relaciones más famosas de la física. Esta relación, junto con las leyes primera y tercera de Newton, suele ser el punto de partida para la instrucción mecánica en la escuela secundaria y la física de pregrado. La instrucción mecánica a menudo se divide en tres áreas diferentes: fuerzas en sistemas estacionarios, movimiento de una partícula sometida a una fuerza y problemas de impacto. Al enfocarse en cada área individualmente, es posible comenzar a desarrollar una comprensión física de los fenómenos físicos importantes.
Cuando los ingenieros aplican estos principios a problemas realistas, les resulta útil tener un marco más general, uno que proporcione una base común para desarrollar modelos matemáticos útiles. Para proporcionar este marco, desarrollamos una ley física llamada Conservación del Momento Lineal que, con pocas restricciones, es de aplicación universal. Luego, como hicimos con masa y carga, exploraremos los supuestos de modelado que los ingenieros suelen usar cuando construyen modelos matemáticos de sistemas físicos.
Al desarrollar un concepto contable para una nueva propiedad, hay cuatro preguntas que deben ser respondidas. Cuando se aplica al impulso lineal, las preguntas se vuelven
- ¿Qué es el impulso lineal?
- ¿Cómo se puede almacenar el impulso lineal en un sistema?
- ¿Cómo se puede transportar el impulso lineal?
- ¿Cómo se puede crear o destruir el impulso lineal?
Una vez que hayamos respondido a estas preguntas tendremos la ecuación contable adecuada para el impulso lineal de un sistema.
¿Qué es el impulso lineal?
Como punto de partida, consideremos el movimiento de un sistema muy especializado, una partícula. Una partícula es un sistema cerrado que se comporta como si su volumen fuera insignificante y su masa se concentrara en un solo punto. El movimiento de una partícula se describe completamente por su velocidad, y todas las interacciones entre una partícula y su entorno ocurren en un solo punto. Posteriormente consideraremos sistemas más realistas y extendidos de mayor tamaño para los cuales la suposición de partículas es insuficiente; sin embargo, encontraremos que la suposición de partículas suele ser un modelo muy bueno.
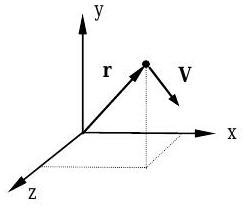
Figura\(\PageIndex{1}\): Partícula con masa\(m\) en posición\(\mathbf{r}\) con velocidad\(\mathbf{V}\).
Para una partícula con masa\(m\) y velocidad\(\mathbf{V}\) como se muestra Figura\(\PageIndex{1}\), el momento lineal de la partícula,\(\mathrm{P}\), se define como el producto de la masa de la partícula y la velocidad de la partícula:\[\mathbf{P}=m \mathbf{V} \nonumber \] Las dimensiones del momento lineal en términos de dimensiones primarias son las producto de las dimensiones de masa y velocidad,\([\mathrm{M}][\mathrm{L}] /[\mathrm{T}]\). Las unidades típicas para el momento lineal están\(\mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\) en SI y\(\mathrm{slug} \cdot \mathrm{ft} / \mathrm{s}\) (o\(\mathrm{lbm} \cdot \mathrm{ft} / \mathrm{s}\)) en USCS.
Es importante señalar que el momento lineal\(\mathbf{P}\), al igual que la velocidad\(\mathbf{V}\), es un vector. Como se muestra en la Figura\(\PageIndex{2}\), los vectores se representan típicamente por flechas. Un vector es una expresión matemática que tiene una magnitud, una dirección y se suma de acuerdo con la ley del paralelogramo. La magnitud del vector describe la “longitud” de la flecha, y si representa una cantidad física, la magnitud incluye tanto un número como las unidades asociadas. La dirección de un vector se especifica en términos de su línea de acción y su sentido. Como se muestra en la Figura\(\PageIndex{2}\) vectores\(\mathbf{P}_{\mathrm{A}}\) y\(\mathbf{P}_{\mathrm{B}}\) tienen la misma magnitud y misma línea de acción pero sentido opuesto. La magnitud de un vector es un número positivo y se representa matemáticamente como\(P_{A}=\left| \mathbf{P}_{A} \right|\). El vector completo se describe dando la magnitud y la dirección de cada vector:\(\mathbf{P}_{A} = P_{A} \ \angle \theta=(5 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}) \ \angle \theta\) y\(\mathbf{P}_{B}=P_{B} \ \angle (\theta+\pi)=(5 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}) \ \angle(\theta+\pi)\), donde todos los ángulos se miden a partir de la línea de referencia.
.jpg)
Figura\(\PageIndex{2}\): Magnitud y dirección de un vector.
Además de magnitud y dirección, los vectores que representan el momento lineal y su transporte también tienen un punto de aplicación. Un vector con un punto de aplicación se denomina vector enlazado. En resumen, un vector de momento lineal se especifica completamente en] ce conocemos su magnitud, dirección y punto de aplicación.
Debido a que el momento lineal de una partícula depende de su masa, el momento lineal es una propiedad extensa. Al igual que con otras propiedades extensas, el momentum lineal tiene una forma intensiva. El momento lineal por unidad de masa, o el momento lineal específico\(\mathbf{p}\), se define como\[\mathbf{p} \equiv \lim _{V\kern-0.5em\raise0.3ex-_{\mathrm{sys}} \rightarrow 0} \frac{\mathbf{P}_{\mathrm{sys}}}{m_{\mathrm{sys}}}=\mathbf{V} \nonumber \] Así, la velocidad de una partícula es realmente solo el momento lineal específico de la partícula.
Es importante señalar que la velocidad, al igual que la posición, siempre se mide en relación con un punto de referencia. Cuando se usa para definir el momento lineal, la velocidad debe medirse en relación con un marco de referencia inercial. Para nuestros propósitos esto significa un sistema de coordenadas que no está rotando ni acelerando con respecto a la Tierra, es decir, un sistema de coordenadas fijo a la Tierra. Además, cualquier sistema de coordenadas que se mueva con una velocidad constante con respecto a la Tierra también es un marco de referencia inercial.
Como mostraremos más adelante, frecuentemente es útil unir el sistema de coordenadas a un sistema móvil si el sistema se mueve con una velocidad constante. Bajo estas condiciones, todas las velocidades se calculan en relación con el sistema de coordenadas móviles. Para el movimiento de la nave espacial, necesitaría usar un marco de referencia no giratorio centrado en el Sol. Consulta cualquier libro de texto de licenciatura en física para conocer más sobre las condiciones de un marco de referencia inercial.
5.1.1 Cinemática de una partícula
Debido a la relación entre la velocidad y el impulso lineal, la comprensión de la cinemática jugará un papel crucial en nuestro estudio del momento lineal. La cinemática es el estudio de la geometría del movimiento sin tener en cuenta la causa del movimiento y proporciona la relación entre la posición\(\mathrm{r}\)\(\mathrm{V}\), velocidad y aceleración\(\mathrm{a}\) de un punto. El vector de velocidad\(\mathrm{V}\) está relacionado con el vector de posición\(\mathrm{r}\) a través de la relación cinemática básica que aprendiste en la física; la velocidad es la primera derivada de la posición:
\[\mathbf{V}=\frac{d \mathbf{r}}{d t} \nonumber \]Las dimensiones de la velocidad son longitud por unidad de tiempo,\([\mathrm{L}] / [\mathrm{T}]\). Las unidades típicas de velocidad están\(\mathrm{m} / \mathrm{s}\) en SI o\(\mathrm{ft} / \mathrm{s}\) en USCS.
La primera derivada de la velocidad (o la segunda derivada de la posición) es el vector de aceleración\(\mathbf{a}\):\[\mathbf{a}=\frac{d \mathbf{V}}{dt} = \frac{d}{dt} \left( \frac{d \mathbf{r}}{dt} \right) \nonumber \] Las dimensiones de la aceleración son longitud por unidad de tiempo al cuadrado,\([\mathrm{L}] /[\mathrm{T}]^{2}\). Las unidades típicas para aceleración están\(\mathrm{m} / \mathrm{s}^{2}\) en SI o\(\mathrm{ft} / \mathrm{s}^{2}\) en USCS.
Movimiento rectilíneo
En movimiento rectilíneo, una partícula solo puede moverse a lo largo de una línea recta. Bajo estas condiciones solo se requiere una coordenada espacial\(x\), digamos, para describir la posición de la partícula, y la velocidad y la aceleración se escriben como\[V=\frac{dx}{dt} \quad \text { and } \quad a=\frac{dV}{dt}=\frac{d^{2} x}{d t^{2}} \nonumber \] Estas relaciones son más útiles cuando la posición\(x\), la velocidad\(V\) y la aceleración\(a\) son todas funciones de tiempo. Bajo condiciones de movimiento rectilíneo, un valor numérico positivo para la velocidad implica que la partícula se mueve en la misma dirección que el\(x\) eje positivo. De igual manera, un valor numérico positivo para la aceleración implica que la velocidad de la partícula va aumentando a medida que se mueve en la dirección del\(x\) eje positivo.
Una expresión alternativa para la aceleración a veces es útil si la aceleración y la velocidad se conocen como funciones de posición, por ejemplo\(V=V(x)\) y\(a=a(x)\). Bajo estas condiciones la aceleración puede escribirse como\[\begin{array} x &= f_{x}(t) \\ V &= f_{V}(x) \quad \rightarrow \quad a \equiv \frac{dV}{dt}=\overbrace{ \left( \frac{dV}{dx} \right) \underbrace{ \left( \frac{dx}{dt} \right)}_{=V} }^{\text {Chain Rule of Differentiation}} =V \frac{d V}{d x} \\ a &= f_{a}(x) \end{array} \nonumber \] usando la regla de la cadena de diferenciación del cálculo. Tenga en cuenta que la notación\(f(t)\) "" se lee como “una función de”\(t\).
Una de las tareas comunes de la cinemática es integrar la aceleración (tasa de cambio temporal, o primera derivada, de velocidad) de un punto con respecto al tiempo o con respecto a la posición. No memorizar las fórmulas que se describen a continuación. Cada uno de los resultados es diferente pero el enfoque es el mismo. ¡Aprende el proceso, no el resultado!
Caso I: La aceleración se conoce como una función del tiempo, e.g\(a=f(t)\). Para encontrar la velocidad, integre con respecto al tiempo de la siguiente manera:\[a = f(t) = \frac{dV}{dt} \rightarrow dV = f(t) dt \quad \rightarrow \quad V - V_{o} = \int\limits_{t_o}^t f(t) \ dt \nonumber \]
Práctica: (a) Dado que\(a=bt\) y\(V=V_{o}\) en\(t=0 \mathrm{~s}\), desarrollar una ecuación para la velocidad\(V\). b) Determinar la velocidad a\(t=5 \mathrm{~s}\), si\(b=15 \mathrm{~m} / \mathrm{s}^{3}\) y\(V_{o}=20 \mathrm{~m} / \mathrm{s}\).
Caso II: La aceleración se conoce como una función de la posición, e.g\(a=f(x)\). La velocidad se puede determinar integrando con respecto a la posición de la siguiente manera:\[a = f(x) = V \frac{dV}{dx} \quad \rightarrow \quad V \ dV = f(x) dx \quad \rightarrow \quad \frac{V^2}{2}-\frac{V_{o}^2}{2} = \int\limits_{x_{o}}^{x} f(x) \ dx \nonumber \]
Práctica: (a) Dado que\(a=c x\) y\(V=V_{o}\) en\(x=0\), desarrollar una ecuación para la velocidad\(V\). b) Determinar la velocidad a\(x=5 \mathrm{~m}\), si\(c=10 \mathrm{~s}^{-2}\) y\(V_{o}=10 \mathrm{~m} / \mathrm{s}\).
Caso III: La aceleración se conoce como una función de la velocidad, e.g\(a=f(V)\). La velocidad se puede determinar integrando con respecto al tiempo o posición de la siguiente manera:\[\begin{align*} & a = f(V) = \frac{dV}{dt} &\rightarrow \quad & dt = \frac{dV}{f(V)} &\rightarrow \quad & t - t_{o} = \int\limits_{V_o}^{V} \frac{dV}{f(V)} \\ & a = f(V) = V \frac{dV}{dx} &\rightarrow \quad & dx =\left[ \frac{V}{f(V)} \right] dV &\rightarrow \quad & x - x_{o} = \int_{V_o}^{V} \left[ \frac{V}{f(V)} \right] \ dV \end{align*} \nonumber \]
Práctica: (a) Dado que\(a=b V^2\) y\(V=V_{o}\) en\(x=x_{o}\), desarrollar una ecuación para la velocidad\(V\). (b) Dado que\(a=b V^2\) y\(V=V_{0}\) a\(t=t_{o}\), desarrollar una ecuación para la velocidad\(V\).
Caso IV: La aceleración es una constante, e.g\(a = \text{constant}\). La velocidad se puede determinar integrando con respecto al tiempo o posición de la siguiente manera:\[ a=\text { constant } \quad \rightarrow \quad \begin{array} a a = \dfrac{d V}{d t} & \rightarrow & dV = a \ dt \quad\quad \rightarrow \quad V - V_{o} = a \left( t-t_{o} \right) \\ a=V \dfrac{dV}{dx} & \rightarrow & V \ dV = a \ dx \quad \rightarrow \quad \dfrac{V^2}{2}-\dfrac{V_{o}^2}{2} = a \left( x-x_{o} \right) \end{array} \nonumber \]
Práctica: Partiendo de la definición de velocidad\(V = d x / d t\), demostrar que la posición puede ser descrita por una ecuación de la forma\(x - x_{o} = V_{o} t +(1 / 2) a t^{2}\).
Movimiento curvilíneo plano
En el movimiento curvilíneo plano (o bidimensional), el movimiento se limita a un plano. Escribir el vector de posición\(\mathbf{r}\) (Figura\(\PageIndex{3}\)) para un punto en el plano en términos de sus componentes rectangulares da\[\mathbf{r} = x \mathbf{i} + y \mathbf{j} \nonumber \] dónde\(\mathbf{i}\) y\(\mathbf{j}\) son los dos vectores unitarios ortogonales\(x\) y y\(y\) son las distancias correspondientes medidas en la dirección de cada vector de unidad.
.png)
Figura\(\PageIndex{3}\): Coordenadas rectangulares
Diferenciando la Ec. \(\PageIndex{7}\)según lo requerido por la Ec. \(\PageIndex{3}\)da el vector de velocidad en términos de sus componentes
\[\begin{align} \mathbf{V} &= \frac{d}{dt} (x \mathbf{i} + y \mathbf{j}) \nonumber \\[4pt] &=\frac{d(x \mathbf{i})}{dt} + \frac{d(y \mathbf{j})}{dt} = \left( \frac{dx}{dt} \mathbf{i} +x \cancel{ \frac{d \mathbf{i}}{dt} }^{=0} \right) + \left( \frac{dy}{dt} \mathbf{j} + y \cancel{ \frac{d \mathbf{j}}{dt} }^{=0} \right) \\[4pt] &= \left( \frac{dx}{dt} \right) \mathbf{i} + \left(\frac{dy}{dt}\right) \mathbf{j} \nonumber \\[4pt] &=V_{x} \mathbf{i} + V_{y} \mathbf{j} \nonumber \end{align} \nonumber \]
donde\(V_{x}\) y\(V_{y}\) son los componentes de velocidad en las\(y\) direcciones\(x\) y, respectivamente. Recuerda de tu estudio de cálculo que la derivada de una constante, como el vector unitario\(\mathbf{i}\), es idéntica a cero. De igual manera, se puede demostrar que el vector de aceleración tiene los componentes:\[\begin{align} \mathbf{a} &=\frac{d \mathbf{V}}{dt} = \frac{d}{dt} \left( V_{x} \mathbf{i} + V_{y} \mathbf{j} \right) \nonumber \\[4pt] &=\frac{d V_{x}}{dt} \mathbf{i} + \frac{d V_{y}}{dt} \mathbf{j} \\[4pt] &=a_{x} \mathbf{i} + a_{y} \mathbf{j} \nonumber \end{align} \nonumber \] dónde\(a_{x}\) y\(a_y\) son los componentes de velocidad en las\(y\) direcciones\(x\) y, respectivamente.
Movimiento relativo
Recordemos que cuando se está calculando el momento lineal de un sistema, todas las velocidades deben medirse con respecto a un marco de referencia inercial, es decir, no acelerado. Así, si la velocidad se mide en un marco de referencia de aceleración, será necesario determinar la velocidad absoluta antes de poder calcular el momento lineal del sistema. Además, si un sistema se traslada a velocidad constante, a veces simplificará un problema calcular el momento lineal con respecto a este marco de referencia inercial móvil.
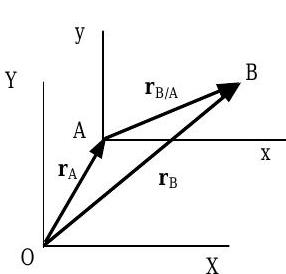
Figura\(\PageIndex{4}\): Posición relativa.
El vector\(\mathbf{r}_{B / A}\) de posición relativa del punto\(B\) con respecto al punto\(A\) (Ver Figura\(\PageIndex{4}\)) se define por la relación:\[ \mathbf{r}_{B/A} = \mathbf{r}_B - \mathbf{r}_A \nonumber \]
donde tanto el vector\(\mathbf{r}_A\) de posición del punto\(A\) como el vector\(\mathbf{r}_B\) de posición del punto\(B\) se miden con respecto al punto\(O\), el origen del sistema de coordenadas XYZ. Dada la posición relativa del punto\(B\) con respecto al punto\(A\) y la posición absoluta del punto\(A\), la Ec. \(\PageIndex{10}\)se puede reescribir de la siguiente manera para encontrar la velocidad absoluta del punto\(B\):\[\mathbf{r}_{B} = \mathbf{r}_{A}+\mathbf{r}_{B / A} \nonumber \]
Se pueden escribir relaciones similares para las velocidades relativas y absolutas de los puntos\(A\) y\(B\):\[\begin{align} \mathbf{V}_{B / A} = \mathbf{V}_{B} - \mathbf{V}_{A} & \rightarrow & \mathbf{V}_{B} = \mathbf{V}_{A} + \mathbf{V}_{B / A} \\ \mathbf{a}_{B / A} = \mathbf{a}_{B} - \mathbf{a}_{A} & \rightarrow & \mathbf{a}_{B} = \mathbf{a}_{A} + \mathbf{a}_{B / A} \end{align} \nonumber \]
Imagínese que un vagón plano de ferrocarril está acelerando y moviéndose hacia la derecha con una velocidad instantánea de\(5 \mathrm{~m} / \mathrm{s}\) medida por un observador en el suelo. Un montacargas ubicado en la plataforma del carro plano se mueve con una velocidad\(3 \mathrm{~m} / \mathrm{s}\) medida por un observador sentado en el carro plano móvil. Ambos observadores ven las direcciones izquierda y derecha de manera similar.
Determinar la velocidad absoluta de la carretilla elevadora, es decir, la velocidad de la carretilla elevadora medida por un observador en el suelo,
a) si el observador sentado en el carro plano ve el montacargas moviéndose a su izquierda y
b) si el observador sentado en el carro plano ve el montacargas moviéndose a su derecha.
Solución
La siguiente ecuación define la velocidad relativa de la carretilla elevadora con respecto al carro plano:\[\mathbf{V}_{\text {forklift / flat car}} = \mathbf{V}_{\text {forklift}} - \mathbf{V}_{\text {flatcar}} \quad \rightarrow \quad \mathbf{V}_{\text {forklift}} = \mathbf{V}_{\text {flatcar}} + \mathbf{V}_{\text {forklift / flatcar}} \nonumber \]
Ahora supongamos que el eje positivo para nuestro sistema de coordenadas apunta hacia la derecha.
a)
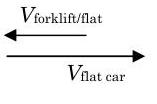
Figura\(\PageIndex{5}\): El montacargas se mueve hacia la izquierda según lo observado por un observador en el carro plano.
\[\begin{aligned} \rightarrow + \quad V_{\text {forklift}} &= V_{\text {flatcar}} -V_{\text {forklift / flatcar}} \\ &=(5 \mathrm{~m} / \mathrm{s}) - (3 \mathrm{~m} / \mathrm{s}) \\ &= 2 \mathrm{~m} / \mathrm{s} \\ \mathbf{V}_{\text {forklift}} &= 2 \mathrm{~m} / \mathrm{s} \text { to the right.} \end{aligned} \nonumber \]
b)
.png)
Figura\(\PageIndex{6}\): El montacargas se mueve hacia la derecha según lo observado por un observador en el carro plano.
\[\begin{aligned} \rightarrow+ \quad V_{\text {forklift}} &= V_{\text {flatcar}} + V_{\text {forklift / flatcar}} \\ &= (5 \mathrm{~m} / \mathrm{s}) + (3 \mathrm{~m} / \mathrm{s}) \\ &= 8 \mathrm{~m} / \mathrm{s} \\ \mathbf{V}_{\text {forklift}} &= 8 \mathrm{~m} / \mathrm{s} \text { to the right.} \end{aligned} \nonumber \]
5.1.2 ¿Cómo se puede almacenar el impulso lineal en un sistema?
El momento lineal se almacena en el movimiento de la masa de un sistema; por lo tanto, cualquier sistema que tenga masa tiene la capacidad de almacenar impulso lineal. Debido a que es una propiedad extensa, el momento lineal de un sistema se puede encontrar sumando el impulso lineal de cada masa dentro del sistema. Para un sistema que consiste en\(\mathrm{N}\) partículas, el momento lineal del sistema\(\mathbf{P}_{\text {sys}}\) se encuentra sumando el momento lineal de las\(\mathbf{N}\) partículas en el sistema,\[\mathbf{P}_{\mathrm{sys}} = \sum_{j=1}^{N} \mathbf{P}_{j} = \sum_{j=1}^{N} m_{j} \mathbf{V}_{j} \nonumber \]
Para un sistema continuo, esta suma se realiza utilizando una integral sobre el volumen del sistema:\[\mathbf{P}_{\mathrm{sys}}=\int\limits_{V\kern-0.5em\raise0.3ex-_{\mathrm{sys}}} ( \mathbf{V} \rho) \ d V\kern-0.8em\raise0.3ex- \nonumber \] donde en general la velocidad y la densidad pueden variar tanto con el tiempo como con la posición.
Centro de masa
Para calcular el momento lineal para un sistema extendido, es decir, algo que no sea una partícula, es necesario evaluar la integral en la Ec. \(\PageIndex{15}\). Afortunadamente este proceso puede simplificarse mucho introduciendo el concepto de centro de masa. El centro de masa es el punto donde se puede suponer que toda la masa para un sistema se concentra para fines de calcular el momento lineal. Como veremos más adelante, esto hace que la evaluación del impulso lineal sea una tarea más sencilla.
La velocidad del centro de masa,\(\mathbf{V}_{G}\), se define por la siguiente ecuación:\[\mathbf{P}_{sys} = m_{sys} \mathbf{V}_{G} \equiv \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} (\mathbf{V} \rho) \ d V\kern-0.8em\raise0.3ex- \quad \rightarrow \quad \mathbf{V}_{G} = \frac{1}{m_{sys}} \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} (\mathbf{V} \rho) \ d V\kern-0.8em\raise0.3ex- \nonumber \] Así la velocidad del centro de masa es igual al momento lineal del sistema dividido por la masa del sistema.
La posición del centro de masa,\(\mathbf{r}_{G}\), es el promedio ponderado en masa de la posición de toda la masa dentro del sistema:\[\mathbf{r}_{G} = \frac{1}{m_{sys}} \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} \mathbf{r} \rho \ d V\kern-0.8em\raise0.3ex- \nonumber \] En la superficie de la tierra, la ubicación del centro de masa es esencialmente la misma que la ubicación del centro de gravedad. Por experiencia, sabemos que un objeto suspendido de su centro de gravedad no tiene tendencia a girar, es decir, está perfectamente equilibrado. Cuando la densidad de un sistema es uniforme, la ubicación del centro de masa es idéntica a la del centroide del volumen del sistema. La ubicación del centroide para las formas más comunes ha sido tabulada y se puede encontrar en manuales matemáticos y físicos.
Un sistema consta de tres partículas con masa, velocidad y posiciones como se indica en la tabla.
| Partícula | \( m \ \text{(kg)}\) | \(\mathbf{r} \ \text{(m)}\) | \(\mathbf{V} \ \text{(m} / \text{s)}\) |
|---|---|---|---|
| 1 | \ (m\\ texto {(kg)}\) ">\(15\) | \ (\ mathbf {r}\\ texto {(m)}\) ">\(3 \mathbf{i} + 3 \mathbf{j}\) | \ (\ mathbf {V}\\ texto {(m}/\ texto {s)}\) ">\(5 \mathbf{i} + 5 \mathbf{j}\) |
| 2 | \ (m\\ texto {(kg)}\) ">\(10\) | \ (\ mathbf {r}\\ texto {(m)}\) ">\(-4 \mathbf{i} + 2 \mathbf{j}\) | \ (\ mathbf {V}\\ texto {(m}/\ texto {s)}\) ">\(3 \mathbf{i} - 5 \mathbf{j}\) |
| 3 | \ (m\\ texto {(kg)}\) ">\(5\) | \ (\ mathbf {r}\\ texto {(m)}\) ">\(1 \mathbf{i} + 2 \mathbf{j}\) | \ (\ mathbf {V}\\ texto {(m}/\ texto {s)}\) ">\(2 \mathbf{i} - 2 \mathbf{j}\) |
Determine lo siguiente para el sistema:
(a) Momento lineal, pulg\(\mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\).
(b) Velocidad del centro de masa, en\(\mathrm{m} / \mathrm{s}\).
(c) Ubicación del centro de masa, en\(\mathrm{m}\).
Solución
Conocido: Descripción de un sistema con información pertinente
Buscar: Calcular el impulso lineal para cada sistema.
Dado: Ver a continuación en cada ejemplo.
Análisis
a) Utilizar la definición de impulso lineal.
\[\begin{aligned} \mathbf{P}_{\mathrm{sys}} &= \mathbf{P}_{1} + \mathbf{P}_{2} + \mathbf{P}_{3} \\ &=m_1 \mathbf{V}_{1} +m_2 \mathbf{V}_{2} + m_3 \mathbf{V}_{3} \\ &= (15 \mathrm{~kg}) \left[ \left( 5 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{i} + \left( 5 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{j} \right] + (10 \mathrm{~kg}) \left[ \left( 3 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{i} - \left(5 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{j} \right] + (5 \mathrm{~kg}) \left[ \left( 2 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{i} - \left(2 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \mathbf{j} \right] \\ &= \left[ (75+30+10) \mathbf{i} + (75-50-10) \mathbf{j} \right] \left(\frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}} \right) \\ &= (115 \mathbf{i} + 15 \mathbf{j}) \left( \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}}\right) \text { or } \left( 115 \ \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}} \right) \mathbf{i} + \left( 15 \ \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}} \right) \mathbf{j} \end{aligned} \nonumber \]
(b) Utilizar la ecuación definitoria para la velocidad del centro de masa
(c) Utilizar la ecuación definitoria para la ubicación del centro de masa
Movimiento plano de un cuerpo rígido
Muchos sistemas físicos de interés pueden modelarse como un cuerpo rígido. Un cuerpo rígido es un cuerpo que no se deforma, es decir, la distancia relativa entre dos puntos cualesquiera del cuerpo permanece constante.
En este curso vamos a restringir la mayor parte de nuestras discusiones a lo que se conoce como movimiento plano. El movimiento plano ocurre cuando cualquier punto del cuerpo viaja en un plano y los planos formados por el lugar de cada punto en el cuerpo son todos paralelos a un plano de referencia común. El movimiento plano de un cuerpo rígido se puede clasificar como traslación, rotación alrededor de un eje fijo o movimiento plano general, que es una combinación de traslación y rotación; ver Figura\(\PageIndex{7}\):
 a) Traducción rectilínea
a) Traducción rectilínea.jpg) b) Traducción curvilínea
b) Traducción curvilínea
.jpg) c) Rotación alrededor de un eje
c) Rotación alrededor de un eje.jpg) d) Movimiento general del plano
d) Movimiento general del plano- Traducción. Si alguna línea recta dentro del cuerpo permanece paralela a sí misma a medida que el cuerpo se mueve, decimos que el movimiento del cuerpo es traslación. Si un punto en el cuerpo también sigue una línea recta, decimos que el movimiento es de traslación rectilínea. Si por otro lado, un punto en el cuerpo sigue un camino curvo, decimos que el movimiento es de traslación curvilínea. La velocidad para cada punto en un cuerpo de traducción se escribe en coordenadas rectangulares como\(\mathbf{V}=V_{x} \mathbf{i} + V_{y} \mathbf{j}\).
- Rotación alrededor de un eje fijo. Si todos los puntos de un cuerpo rígido se mueven en planos paralelos y siguen círculos concéntricos alrededor del mismo eje fijo, decimos que el cuerpo gira alrededor de un eje fijo. Llamamos al eje fijo el eje de rotación. Bajo estas condiciones la velocidad de cada punto en el cuerpo puede ser descrita por la relación\(\mathbf{V}=r \omega \mathbf{e}_{\theta} = r \omega(-(\sin \theta) \mathbf{i} + (\cos \theta) \mathbf{j})\)
- Movimiento general del plano. La experiencia ha demostrado que el movimiento plano de cualquier cuerpo rígido puede describirse como una combinación de rotación de un cuerpo rígido alrededor de un eje de rotación de traslación.
La cinemática del movimiento plano general es complicada y su estudio se retrasará hasta un curso posterior. Pasaremos la mayor parte de nuestro tiempo abordando la traslación rectilínea y la rotación alrededor de un eje fijo. Debido a esto, es importante que puedas identificar los tres tipos de movimiento plano.
5.1.3 ¿Cómo se puede transportar el impulso lineal a través de los límites de un sistema?
El impulso lineal puede transportarse a través de los límites del sistema mediante dos mecanismos diferentes: fuerzas y flujo másico. Al igual que con el momento lineal, tanto las fuerzas como los transportes masivos de impulso lineal son vectores y para especificar cada uno requiere que se especifique la magnitud, dirección (sentido y línea de acción) y el punto de aplicación.
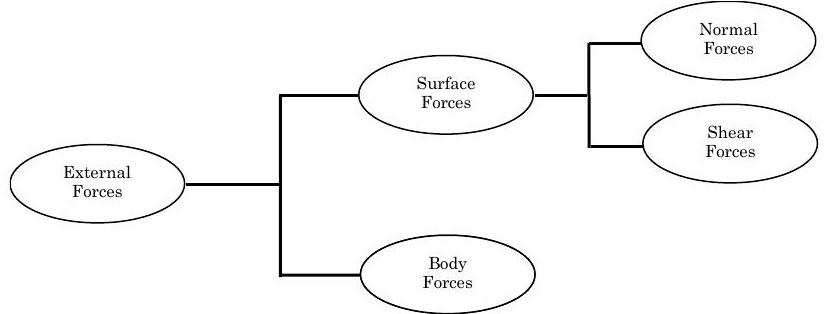
Figura\(\PageIndex{8}\): Clasificación de las Fuerzas Externas
Transporte de momentum lineal con fuerza
La experiencia ha demostrado que el impulso lineal de un sistema cerrado sólo puede ser cambiado por la aplicación de una fuerza externa (Así fue como Newton declaró originalmente su segunda ley). Por lo tanto, una fuerza externa aplicada a un sistema cerrado debe transferir impulso lineal entre el sistema y su entorno. Más específicamente,\[\mathbf{F}_{\text {external}} \equiv \dot{\mathbf{P}}_{\text {Force}} = \left\{ \begin{array}{c} \text { transport rate of linear momentum } \\ \text { across a boundary due to a force } \end{array} \right\} \nonumber \] donde la dirección del flujo de impulso está en la misma dirección que la fuerza.
Una fuerza externa es un mecanismo para transferir impulso lineal y es una tasa de transporte para el impulso lineal a través del límite entre un sistema y su entorno. Una fuerza es un vector con todas las propiedades discutidas anteriormente. Las dimensiones primarias para la fuerza son\([\mathrm{M}][\mathrm{L}] /[\mathrm{T}]^{2}\), que son las dimensiones de [Momento Lineal]/[Tiempo]. La unidad típica para la fuerza es un newton\( (\text{N}) \) en SI y una libra-fuerza\( (\text{lbf}) \) en USCS.
Cuando varias fuerzas actúan sobre un sistema, la tasa neta de transporte de impulso lineal a un sistema con las fuerzas externas se escribe matemáticamente de la siguiente manera: Las fuerzas\[\sum_{j} \mathbf{F}_{\text {ext } j} \equiv \left\{ \begin{array}{c} net \text { transport rate of linear momentum} \\ \text {into the system with force} \end{array}\right\} \nonumber \] externas, como se muestra en la Figura\(\PageIndex{8}\), se pueden clasificar como fuerzas superficiales o fuerzas corporales. Las fuerzas superficiales se pueden clasificar además como fuerzas normales o cortantes.
Fuerzas del Cuerpo
Una fuerza corporal siempre actúa de manera distribuida dentro del volumen del sistema y es el resultado de colocar el sistema en un campo de fuerza, por ejemplo, un campo gravitacional, un campo eléctrico o un campo magnético. Debido a esto, a una fuerza corporal a veces se le llama “fuerza a distancia”. Al actuar sobre el volumen del sistema, la fuerza corporal sólo puede calcularse una vez definido el sistema.
La fuerza corporal que ocurre más comúnmente es el peso, la fuerza ejercida por la Tierra sobre una masa colocada en el campo gravitacional de la Tierra. Si bien una fuerza corporal actúa en todo el sistema, su efecto se representa frecuentemente como una fuerza concentrada que actúa en un punto específico dentro del sistema. Cuando la intensidad del campo es espacialmente uniforme como lo es en el campo gravitacional de la Tierra, se supone que el peso de un objeto actúa en el centro de gravedad del sistema. Cerca de la superficie de la Tierra, cuando un objeto está suspendido de su centro de gravedad, el objeto estará perfectamente equilibrado.
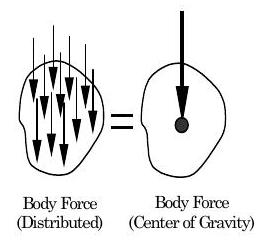
Figura\(\PageIndex{9}\): Fuerza corporal debida a la gravedad
Determinar la magnitud, dirección y punto de aplicación del vector de peso para los sistemas A, B y C. Cada sistema está hecho de un material con una densidad de\(900 \mathrm{~kg} / \mathrm{m}^{3}\). En cada caso, dibuje su sistema y ubique el centro de gravedad. [Pista: Podrías probar tu libro de física, tu cálculo o una buena tabla de matemáticas para encontrar la ubicación del centroide de estos volúmenes.]
| Sistema A | Sistema B | Sistema C |
|---|---|---|
| Cilindro circular derecho con diámetro\(D = 20 \ \text{cm}\) y altura\(H = 40 \ \text{cm}\). |
Un cono circular derecho con diámetro\(D = 20 \ \text{cm}\) y altura\(H = 40 \ \text{cm}\). |
Un hemisferio de diámetro\(D = 20 \ \text{cm}\). |
Fuerzas de superficie
Una fuerza superficial se caracteriza por tener un punto o puntos de contacto físico en la superficie limítrofe, y por esta razón a veces se la denomina fuerza de contacto. Físicamente, las fuerzas superficiales siempre actúan sobre un área finita, es decir, son fuerzas distribuidas.
Normalmente, generalmente representamos las fuerzas superficiales por una sola fuerza concentrada (ver Figura\(\PageIndex{10}\)). Cuando una fuerza superficial actúa sobre una superficie plana y el área es pequeña o la fuerza se distribuye uniformemente sobre el área, es razonable modelar la fuerza distribuida como una sola fuerza concentrada con un punto de aplicación en el centroide del área.
.png)
Figura\(\PageIndex{10}\): Fuerzas superficiales
Cuando la superficie es curva o la fuerza distribuida no es uniforme, todavía se puede utilizar una sola fuerza concentrada para modelar la fuerza distribuida; sin embargo, el punto exacto de aplicación debe calcularse cuidadosamente y no es necesariamente el centroide del área sobre la que actúa la fuerza distribuida.
Cada fuerza superficial puede, si es necesario, descomponerse aún más en dos componentes: uno normal y otro de cizallamiento, como se muestra en la Figura\(\PageIndex{11}\). La línea de acción de una fuerza normal es perpendicular a la superficie en el punto de aplicación, y la línea de acción de una fuerza de corte es tangente a la superficie en el punto de aplicación. Algunas fuerzas externas son, por su propia naturaleza, fuerzas puramente normales o puramente cortantes. Por ejemplo, la fuerza producida por la presión de la atmósfera sobre cualquier superficie es siempre una fuerza normal, mientras que la fuerza debida a la fricción es siempre una fuerza de cizallamiento.
.png)
Figura\(\PageIndex{11}\): Fuerzas normales y cortantes.
Fuerzas superficiales debidas a la presión
Una de las fuerzas más ubicuas en nuestras vidas es la fuerza de la atmósfera. Debido a esto debemos considerar cómo determinar las fuerzas superficiales debidas a la presión. Por definición, la presión se define como la fuerza por unidad de área. Las dimensiones para la presión son\([\mathrm{F}]/[\mathrm{L}]^2 = \{ [\mathrm{M}][\mathrm{L}]/[\mathrm{T}]^2 \} / [\mathrm{L}]^2 = [\mathrm{M}][\mathrm{L}]^{-1} [\mathrm{T}]^{-2}\). Las unidades típicas para presión son newton por metro cuadrado o pascales\((\mathrm{Pa})\) en SI con\(1 \ \text{Pa} = 1 \ \text{N}/\text{m}^2\). En USCS, las unidades son libras-fuerza por pulgada cuadrada (\(\text{psi}\)o\(\text{lbf}/\text{in}^2\)) o libras-fuerza por pie cuadrado (\(\text{psf}\)o\(\text{lbf}/\text{ft}^2\)) con\(144 \ \text{psi} = 144 \ \text{lbf}/\text{in}^2 = 1 \ \text{lbf}/\text{ft}^2\).
El valor estándar de la presión atmosférica en la superficie de la tierra es\(P_{\text{atm}} = 101325 \ \text{Pa} = 101.325 \ \text{kPa} = 14.696 \ \text{lbf}/\text{in}^2\). Estos valores se redondean frecuentemente a\(101.3 \ \text{kPa}\) y\(14.7 \text{lbf}/\text{in}^2\).
Para evaluar la fuerza debida a la presión que actúa sobre una superficie debemos definir primero la superficie (ver Figura\(\PageIndex{12}\)). Matemáticamente, la fuerza se calcula utilizando la integral de la presión sobre el área superficial como se muestra a continuación:
\[ \mathbf{F}_{\text{pressure}} = - \int\limits_{A_{\text{surface}}} \mathbf{n} P \ dA \nonumber \]donde\(P\) está la presión que actúa sobre el límite,\(\mathbf{n}\) es el vector normal unitario que apunta desde el sistema hacia el entorno, y\(dA\) es el área diferencial sobre la cual actúa la presión. Así, la dirección de la fuerza de presión siempre está en el sistema.
.jpg)
Figura\(\PageIndex{12}\): Geometría para el cálculo de la fuerza de presión.
La aplicación más simple y también la más común es aquella en la que la presión es uniforme y la superficie es plana. Bajo estas condiciones Ec. \(\PageIndex{20}\)se puede simplificar en gran medida ya que tanto el vector normal de la unidad como la presión salen fuera de la integral:
\[ \begin{align} \mathbf{F}_{\text{pressure}} &= - \int\limits_{A_{\text{surface}}} \mathbf{n} P \ dA \nonumber \\ &= -(\mathbf{n} P) \underbrace{ \int\limits_{A_{\text{surface}}} dA }_{= A_{\text{surface}}} = - P A_{\text{surface}} \mathbf{n} \end{align} \nonumber \]
En palabras, esto dice que la fuerza de presión sobre una superficie plana debido a una presión uniforme es un vector que es perpendicular a la superficie, apunta al sistema, y tiene una magnitud igual a\(P A_{\text {surface, }}\), el producto de la presión y el área superficial. Además, se puede demostrar (después de estudiar el momento angular) que el punto de aplicación de la fuerza está en el centroide de la superficie.
Como ejemplo, considere un sólido triangular con ancho constante en el papel como se muestra en la Figura\(\PageIndex{13}\). Una presión uniforme actúa en cada uno de los tres lados como se muestra en la figura. Dado que cada presión es uniforme y las superficies son planas, el vector de fuerza de presión equivalente se puede calcular usando la Ec. \(\PageIndex{21}\). Para cada lado, el vector de fuerza apunta hacia la superficie, es normal a la superficie, y tiene una magnitud igual al producto de la presión y la superficie sobre la que actúa la presión uniforme.
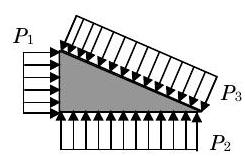 a) Distribuciones de presión
a) Distribuciones de presión.jpg) b) Vectores de fuerza de presión
b) Vectores de fuerza de presiónCon frecuencia, tendremos sistemas que están sometidos a presión atmosférica sobre todo el límite del sistema. Imagina por un minuto cualquier objeto en particular que te gustaría, digamos tu auto o una manzana colgada de una cuerda, que esté sujeta a una presión atmosférica uniforme por todos lados. ¿Cuál es la fuerza neta de la atmósfera sobre el objeto? Con base en tu experiencia, supongo que dirías que la fuerza neta debida a la presión atmosférica es cero. Puedes repetir este experimento y encontrarás que la fuerza neta sobre cualquier objeto rodeado por una presión uniforme será cero independientemente de la forma del objeto o del valor de la presión.
Esto nos lleva a otro resultado interesante. Considere el sólido de forma irregular que se muestra en la Figura\(\PageIndex{14}\). Imagínese que el objeto está sometido a una presión uniforme en todos los lados y que los vectores de fuerza de presión resultantes se muestran en la figura. Ahora sabemos por experiencia que si las únicas fuerzas se deben a la presión uniforme entonces no hay fuerza neta sobre el objeto debido a las presiones. Si esto no fuera cierto, entonces el objeto tendría tendencia a moverse (y patentaríamos este dispositivo y nos retiraríamos al Caribe). Esto debe significar que la fuerza de presión que actúa sobre el lado izquierdo del sólido debe ser igual a la suma de las fuerzas de presión que actúan sobre el lado derecho del sólido. Como hemos demostrado, la fuerza de presión es proporcional a la superficie. Entonces, ¿por qué el lado izquierdo no tiene más fuerza de presión que el lado derecho? La clave está en la naturaleza vectorial de la fuerza.
.jpg)
Figura\(\PageIndex{14}\): Fuerzas de presión usando áreas proyectadas.
Para ayudarnos a entender este resultado, solo consideremos la fuerza en la\(x\) dirección. Ahora vemos que la fuerza de presión que actúa sobre el lado izquierdo del sólido debe ser igual a los\(x\) -componentes de las fuerzas de presión que actúan sobre el lado derecho del sólido. Sin recurrir a matemáticas complicadas, podemos resumir este resultado de la siguiente manera:
La magnitud de la fuerza de presión en cualquier dirección es igual al producto de la presión y el área proyectada en la dirección deseada.
El área proyectada es el área bidimensional observada cuando la superficie se ve en la dirección de interés. Considera una esfera con diámetro\(D\) y un cilindro con diámetro\(D\) y altura\(H\). Cuando se observa desde cualquier dirección, la esfera parece un círculo con área proyectada\(\pi D^{2} / 4\). Ahora considera el cilindro. Cuando se ve desde cualquier extremo el cilindro también tiene un área proyectada de\(\pi D^{2} / 4\); sin embargo, cuando se ve desde el lado (perpendicular a su eje de simetría), el área proyectada del cilindro es un rectángulo de área\(D H\).
También con frecuencia tendremos problemas donde solo una pequeña porción del límite del sistema está sujeta a presión no atmosférica. Bajo estas condiciones, podemos simplificar enormemente los cálculos de la fuerza de presión “restando” la presión atmosférica. Considere el sólido triangular familiar como se muestra en la Figura\(\PageIndex{15}\).
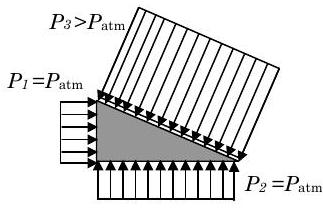
.jpg)
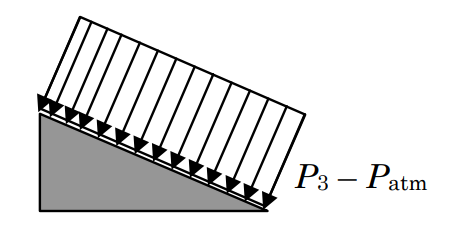.png)
c) Distribución de presión resultante con
\(P_{3, \text{new}} = P_3 - P_{\text{atm}}\)
\[ \mathbf{F}_{\text{net}} = - ( P_3 - P_{\text{atm}}) A_3 \mathbf{n} \nonumber \]
Para este ejemplo, asumiremos que todas las superficies excepto una están sometidas a presión atmosférica y esta superficie tiene una presión uniforme\(P_{3}>P_{\mathrm{atm}}\). Como se muestra en la figura, podemos utilizar la integral estándar para evaluar la fuerza neta debida a las presiones que actúan sobre el sistema. Dado que la fuerza neta debida a una presión atmosférica uniforme en todas las superficies es cero como se muestra en la parte (b) de la Figura\(\PageIndex{15}\) podemos restar esta fuerza cero de la integral. Una vez hecho esto, la integral para la fuerza neta se puede reorganizar como se muestra y descubrimos que la fuerza neta es el resultado de la presión medida con respecto a la presión atmosférica (esto a veces se denomina presión manométrica). Finalmente, como se muestra en la parte (c) la magnitud de la fuerza neta es justa\(\left(P_{3}-P_{\text {atm}}\right) A_{3}\). Ya que\(P_{3}>P_{\text {atm}}\), la flecha de fuerza apunta hacia la superficie 3. Cuando alguna porción del límite de un sistema está sujeta a presión no atmosférica, restar la presión atmosférica simplificará enormemente el cálculo de la fuerza de presión neta.
Para darnos un poco de práctica rápida con estas ideas, considera el ayudante de plomero utilizado para destapar los inodoros. El clásico ayudante de plomero consiste en un hemisferio hueco de goma unido a un palo de madera. El material de goma es flexible y se deformará cuando se empuja contra una superficie. Si se aplica sobre una superficie lisa, como se muestra en la figura, el aire será exprimido fuera del hemisferio. Esto disminuye la presión dentro del hemisferio deformado y hace que el ayudante del plomero se “pegue” a la superficie. ¿Cuál es exactamente la fuerza neta en dirección vertical debido a la presión sobre el ayudante del plomero?
.png)
Figura\(\PageIndex{16}\): El ayudante del plomero.
Solución
Considera el sistema que se muestra arriba por las líneas discontinuas. La copa en contacto con la superficie es de diámetro\(D\). La presión en cada superficie del sistema excepto el extremo abierto de la copa de goma (superficie superior) se somete a presión atmosférica,\(P_{\text{atm}}\). La superficie que cubre el extremo abierto de la copa ve una presión,\(P_{\text{cup}}\) la presión del aire atrapado dentro del hemisferio deformado.
El área proyectada del ayudante del plomero, cuando se ve desde arriba o abajo a lo largo de la dirección vertical, es solo un círculo con área\((\pi / 4) D^{2}\). También, como queremos encontrar la fuerza neta podemos simplemente restar la presión atmosférica.
Así
\[ \begin{align*} & \mathbf{F}_{\text {net pressure}} = -\left(P_{\text {cup}} - P_{\text {atm}}\right) A_{\text {projected}} \mathbf{n} \\ \uparrow+ & F_{\text {net pressure}} = -\left(P_{\text {cup}} - P_{\text {atm}}\right) \left(\frac{\pi}{4} D^{2}\right)(1)=\left(P_{\text {atm}} - P_{\text {cup}}\right) \left(\frac{\pi}{4} D^{2}\right) \\ & \mathbf{F}_{\text {net pressure}} = \left(P_{\text {atm}}-P_{\text {cup}}\right) \left(\frac{\pi}{4} D^{2}\right) \angle 90^{\circ} \quad \text { or } \quad \left(P_{\text {atm}}-P_{\text {cup}}\right) \left(\frac{\pi}{4} D^{2}\right) \uparrow \end{align*} \nonumber \]
Como cabría esperar si\(P_{\text {cup}}<P_{\text {atm}\), la fuerza neta estará arriba (en la\(y\) dirección positiva). Hay al menos otras dos fuerzas que actúan sobre este sistema que regirán si se “pega” o cae: el peso del sistema y la fuerza de la superficie lisa sobre el sistema donde entra en contacto con el hemisferio de goma.
Transporte lineal de momento con flujo másico
Como se mostró anteriormente, cada bulto de masa con una velocidad tiene un impulso lineal. Cuando se permite que la masa fluya a través del límite de un sistema abierto, cada bulto de masa lleva consigo un impulso lineal. Por lo tanto, el momento lineal de un sistema abierto también se puede cambiar mediante el flujo másico que transporta el momento lineal a través del límite del sistema. La velocidad a la que se transporta el momento lineal a través del límite se puede representar por el producto del caudal másico y la velocidad local en el límite, asumiendo que la velocidad es uniforme:\[\dot{\mathbf{P}}_{\text {mass}} = \dot{m} \mathbf{V} = \left\{\begin{array}{c} \text { transport rate of linear momentum } \\ \text { with mass flow } \end{array}\right\} \nonumber \] donde\(\dot{m}\) está el caudal másico en el límite de flujo donde la velocidad\(\mathbf{V}\) es uniforme. La dimensión para esta cantidad es\([\mathrm{M}][\mathrm{L}] /[\mathrm{T}]^{2}\).
Figura\(\PageIndex{17}\): Transporte masivo de momento lineal en un límite.
Para condiciones donde la velocidad no es espacialmente uniforme en el límite del flujo, la tasa de transporte de momento lineal debe calcularse a partir del uso de una integral. En cualquier límite de flujo como se muestra en la Figura\(\PageIndex{17}\), el transporte de impulso lineal fuera del sistema se puede caracterizar por la integral:\[\begin{array} \dot{\mathbf{P}}_{\text {mass, out}} &= \displaystyle \int\limits_{A_{\text {sys}}}(\mathbf{V}) \left( \rho \mathbf{V}_{\text {rel}} \cdot \mathbf{n} \right) \ dA \\ &= \displaystyle \int\limits_{A_{\text {sys}}}(\mathbf{V}) \left(\rho V_{\text {n, rel}}\right) \ dA \end{array} \nonumber \] donde\(\mathbf{V}\) está el vector de velocidad local medido con respecto a un marco de referencia inercial,\(\mathbf{V}_{\text{rel}}\) es el vector de velocidad local medido con respecto a la superficie,\(\mathbf{n}\) es el vector unitario normal a la superficie diferencial\(d A\) y señala desde el sistema, y\(V_{\text{n, rel}} = \mathbf{V}_{\text {rel}} \cdot \mathbf{n}\), la magnitud de la componente normal de la velocidad\(\mathbf{V}_{\text {rel}}\).
Si la velocidad es espacialmente uniforme en la sección transversal del flujo, el transporte de masa del momento lineal se puede escribir en términos del caudal másico en el límite y la velocidad de la siguiente manera:
\[ \begin{align} \dot{\mathbf{P}}_{\text{mass, out}} &= \int\limits_{A_{\text{sys}}} (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) \ dA = (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) \int\limits_{A_{\text{sys}}} dA \nonumber \\[4pt] &= (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) A_{\text{sys}} = \left( \rho V_{\text{n, rel}} A_{\text{sys}} \right) \mathbf{V} \\ &= \dot{m}_{\text{out}} \mathbf{V} \nonumber \end{align} \nonumber \]
Esto a menudo se conoce como flujo unidimensional. Si la velocidad no es uniforme a través del área de flujo, el área de flujo debe dividirse en un número adecuado de áreas donde la velocidad puede asumirse uniforme y la Ec. \(\PageIndex{24}\)se convertirá en una suma. Alternativamente, la distribución de velocidad no uniforme se puede manejar realizando la integral en la Ec. \(\PageIndex{23}\).
El transporte neto de impulso lineal con caudal másico se puede obtener sumando los transportes en todos los límites de flujo:\[\sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \equiv \left\{ \begin{array}{c} net \text { transport rate of linear momentum } \\ into \text { the system with mass flow } \end{array}\right\} \nonumber \] Observe que el transporte neto puede ser positivo o negativo dependiendo de los transportes relativos.
5.1.4 ¿Cómo se puede generar o destruir el impulso lineal en un sistema?
La experiencia ha demostrado que el impulso lineal de un sistema no puede crearse ni destruirse. Reconociendo que el impulso lineal es una propiedad extensa, podemos exponer esta ley de la siguiente manera:
El impulso lineal es una propiedad conservada.
Una vez más se le recuerda que el uso de la palabra “conservación” es diferente en este curso (ES201) al que conoce en física. (Vamos, eche un vistazo a su libro de física y vea qué tipo de problemas resuelven en la sección etiquetada “conservación del impulso lineal”. ¿Los problemas relacionados con la conservación de la energía difieren de los problemas que implican la conservación del impulso lineal?) En este curso, cuando decimos que algo se conserva estamos haciendo una declaración general sobre la forma en que se comporta el mundo y no una suposición modelada específica del problema. De hecho, se podría decir que es incorrecto (si no redundante) escribir en una solución de problemas “supongamos que se conserva el momento lineal (o masa o carga)”. No se pueden invocar leyes físicas básicas asumiendo su existencia. Sería correcto decir “usando (o aplicando) la conservación del impulso lineal (o masa o carga) encontramos que...” Las leyes físicas básicas se aplican lo queramos o no.
5.1.5 ¡Poniéndolo todo junto!
Usando el marco contable, ahora podemos desarrollar la siguiente declaración para la conservación del impulso lineal:\[\left[ \begin{array}{c} \text { Rate of accumulation } \\ \text { of } \\ \text { linear momentum } \\ \text { inside a system } \\ \text { at time } t \ \end{array} \right] = \left[ \begin{array}{c} \text { Net transport rate of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by external forces } \\ \text { at time } t \ \end{array}\right] + \left[\begin{array}{c} \text { Net transport rate of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by mass flow } \\ \text { at time } t \ \end{array}\right] \nonumber \] o en símbolos, la conservación del momento lineal (forma de tasa) se convierte en\[\frac{d \mathbf{P}_{\text {sys}}}{d t} = \sum \dot{\mathbf{P}}_{\text {force}} + \sum_{\text {in}} \dot{\mathbf{P}}_{\text {mass, in}} - \sum_{\text{out}} \dot{\mathbf{P}}_{\text {mass, out}} \nonumber \]
Usando los símbolos más familiares de fuerzas, caudales másicos e impulso lineal específico, la forma de tasa de conservación del momento lineal se vuelve\[\frac{d \mathbf{P}_{\mathrm{sys}}}{d t} = \sum \mathbf{F}_{\text {ext}} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \label{RateFormLN} \] En palabras podríamos decir lo siguiente:
La tasa de cambio temporal del momento lineal del sistema es igual a la tasa neta de transporte de impulso lineal al sistema por fuerzas externas más la tasa neta de transporte de impulso lineal al sistema por flujo másico.
Bajo algunas condiciones, la forma integrada o de tiempo finito es útil. En palabras, la forma de tiempo finito de la conservación del impulso lineal es\[ \left[ \begin{array}{c} \text { Linear } \\ \text { momentum } \\ \text { inside the } \\ \text { system at } \\ \text { time } t_{2} \end{array}\right] - \left[\begin{array}{c} \text { Linear } \\ \text { momentum } \\ \text { inside the } \\ \text { system at } \\ \text { time } t_{1} \end{array}\right] = \left[\begin{array}{c} \text { Net transport of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by external forces } \\ \text { during the period } \Delta t \end{array}\right]+\left[\begin{array}{c} \text { Net transport of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by mass flow } \\ \text { during the period } \Delta t \end{array}\right] \nonumber \]
o en forma de ecuación,\[\Delta \mathbf{P}_{\mathrm{sys}} = \sum_{\text {external}} \left( \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt \right) + \sum_{\text {in}} \left( \int\limits_{t_{1}}^{t_{2}} \left(\dot{m}_{i} \mathbf{V}_{i}\right) \ d t \right) - \sum_{\text {out}} \left(\int\limits_{t_{1}}^{t_{2}} \left(\dot{m}_{e} \mathbf{V}_{e}\right) \ dt \right) \nonumber \] Aunque esta última forma de la ecuación de conservación de momentum lineal parece bastante complicada, en realidad es mucho más sencillo enfocarse en la forma de tasa y luego, si es necesario, realizar la integración requerida para recuperar Ecuación\(\PageIndex{30}\).
Las leyes de Newton se escriben comúnmente de la siguiente manera:
Ley I: Si la fuerza resultante que actúa sobre una partícula es cero, la partícula permanecerá en reposo (si originalmente está en reposo) o se moverá con velocidad constante en línea recta (si originalmente está en movimiento)
Ley II: Si la fuerza resultante que actúa sobre una partícula no es cero, la partícula tendrá una aceleración proporcional a la magnitud de la fuerza resultante y en la dirección de esta fuerza resultante
Ley III: Las fuerzas de acción y reacción entre cuerpos en contacto tienen la misma magnitud, misma línea de acción, y sentido opuesto.
Demostrar que estas tres leyes son satisfechas por la aplicación de la forma tarifaria de la Conservación del Momento Lineal.
Solución
Conocido: las tres leyes de la mecánica de Newton
Encuentra: Demostrar que estas leyes están sustentadas por la conservación del impulso lineal
Dado: Proporcionado según sea necesario.
Análisis:
Primera Ley de Newton: Mira una sola partícula como se muestra en la figura. Para aplicar la conservación del momento lineal, seleccionamos la partícula como sistema y dibujamos un diagrama de interacción de momento lineal (cuerpo libre) para el cuerpo.
.png)
Figura\(\PageIndex{18}\): Un sistema que consiste en una partícula. Diagrama de cuerpo libre de este sistema, que no tiene interacciones con su entorno.
Escribiendo la forma de tasa de conservación del impulso lineal para este sistema tenemos:
\[ \begin{align*} &\frac{d \mathbf{P}_{\text{sys}}}{dt} = \underbrace{ \cancel{ \sum \mathbf{F}_{\text{ext}} } }_{ \begin{array}{c} =0 \text{ because there} \\ \text{are no external} \\ \text{forces} \end{array} } + \underbrace{ \cancel{ \sum_{\text{in}} \dot{m}_i \mathbf{V}_i - \sum_{\text{out}} \dot{m}_e \mathbf{V}_e } }_{\begin{array}{c} =0 \text{ because} \\ \text{it is a closed system} \end{array} } \\ &\frac{d \mathbf{P}_{\text{sys}}}{dt} = 0 \quad \rightarrow \quad 0 = \frac{d \mathbf{P}_{\text{sys}}}{dt} = \frac{ d (m \mathbf{V})}{dt} = m \frac{d \mathbf{V}}{dt} \end{align*} \nonumber \]
Así, ¡\(\dfrac{d \mathbf{V}}{dt} = 0\)y\(\mathbf{V}\) es una constante!
Esto demuestra que sin transportes de impulso lineal por fuerza, es decir, sin fuerzas externas que actúen sobre la partícula, la velocidad de la partícula permanece constante.
Segunda Ley de Newton: El sistema es el mismo que antes, solo que esta vez hay una fuerza que actúa sobre el sistema.
.png)
Figura\(\PageIndex{19}\): Diagrama de cuerpo libre de un sistema constituido por una partícula con una fuerza que actúa sobre ella.
\[ \begin{align*} &\frac{d \text{P}_{\mathrm{sys}}}{dt} = \mathbf{F} + \underbrace{ \cancel{ \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} } }_{\begin{array}{c} =0 \text { because } \\ \text { it is a closed system } \end{array} } \\ &\frac{d \mathbf{P}_{\text {sys}}}{d t} = \mathbf{F} \quad \rightarrow \quad \mathbf{F} = \frac{d \mathbf{P}_{\text {sys}}}{d t} = \frac{d(m \mathbf{V})}{d t} = m \underbrace{\frac{d \mathbf{V}}{d t}}_{= \mathbf{a}} = m \mathbf{a} \end{align*} \nonumber \]
Así\(\mathbf{F}=m \mathbf{a}\) y\(\mathbf{a}=\mathbf{F} / m\).
Esto demuestra que el vector de aceleración es proporcional al vector de fuerza externa, por lo que la magnitud de la aceleración es proporcional a la fuerza aplicada y la dirección es la misma que la dirección de la fuerza aplicada.
Tercera Ley de Newton: Esta vez nuestro sistema es la interfaz o superficie de contacto entre dos partículas que están en contacto. Esta interfaz, como se muestra en el dibujo a continuación\(\mathbf{F}_{\mathrm{A-B}}\), no tiene masa en su interior y es actuada por dos fuerzas: la fuerza de la partícula\(\mathrm{A}\)\(\mathrm{B}\) sobre la partícula y\(\mathbf{F}_{\mathrm{B-A}}\) la fuerza de la partícula\(\mathrm{B}\) sobre la partícula\(\mathrm{A}\).
.png)
Figura\(\PageIndex{20}\): Sistema consistente en la interfaz de contacto entre dos partículas.
Escribir la ecuación de conservación de impulso lineal para este sistema da lo siguiente:
\[ \begin{align*} \underbrace{ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{dt} } }_{\begin{array}{c} =0 \text{ because the system} \\ \text{has no mass, so } \mathbf{P} = 0 \\ \text{for all time.} \end{array} } = \mathbf{F}_{\text{A-B}} + \mathbf{F}_{\text{B-A}} + \underbrace{ \cancel{ \sum_{\text{in}} \dot{m}_i \mathbf{V}_i - \sum_{\text{out}} \dot{m}_e \mathbf{V}_e } }_{\begin{array}{c} =0 \text{ because} \\ \text{it is a closed system} \end{array}} \\ 0 = \mathbf{F}_{\text{A-B}} + \mathbf{F}_{\text{B-A}} \quad \rightarrow \quad \mathbf{F}_{\text{B-A}} = -\mathbf{F}_{\text{A-B}} \end{align*} \nonumber \]
Así, las fuerzas de acción y reacción en un punto de contacto entre dos sistemas son vectores de igual magnitud, signo opuesto, y la misma línea de acción.
Comentario: El punto importante aquí es que las tres leyes mecánicas de Newton se incorporan al principio de Conservación del Momentum Lineal tal como se formula aquí.


