5.2: Conservación de Ecuación de Momento Lineal
- Page ID
- 86366
El punto de partida recomendado para cualquier aplicación de la conservación del momento lineal es la forma de tasa de la ecuación de momento lineal (previamente dada como Ecuación (5.1.28):\[\frac{d \mathbf{P}_{\text {sys}}}{d t} = \sum \mathbf{F}_{\text {ext}} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text{out}} \dot{m}_{e} \mathbf{V}_{e} \nonumber \] donde\(\mathbf{P}_{\text {sys}}\) está el impulso lineal del sistema,\(\mathbf{F}_{\text {ext}}\) es la tasa de transporte del momento lineal por una fuerza externa, y\(\dot{m} \mathbf{V}\) es la tasa de transporte de impulso lineal por flujo másico.
Al aplicar la forma de tasa del momento lineal de conservación a un sistema, hay muchos supuestos de modelado que se utilizan frecuentemente para construir el modelo matemático del sistema físico. Estos se detallan en los siguientes párrafos. Como siempre, debes enfocarte en entender qué significan físicamente las suposiciones y cómo pueden usarse para simplificar las ecuaciones para un sistema dado. No se limite a memorizar los resultados.
Sistema de estado estacionario:
Si un sistema está operando en condiciones de estado estacionario, todas las propiedades intensivas son independientes del tiempo, es decir, los valores de las propiedades intensivas solo pueden variar con la posición. Así, el impulso lineal del sistema es una constante,\(\mathbf{P}_{\text {sys}} = \text{constant}\). Cuando esta suposición se aplica a la conservación de la ecuación de impulso lineal, tenemos
\[\begin{gathered} \cancel{ \underbrace{ \frac{d \mathbf{P}_{\text {sys}}}{d t} }_{ \mathbf{P}_{\text{sys}} = \text{constant} } }^{=0} = \sum \mathbf{F}_{\text {ext}} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \\ 0 = \sum \mathbf{F}_{\text {ext}} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \end{gathered} \nonumber \]En palabras, esto dice que la tasa neta de transporte de impulso lineal hacia el sistema por la fuerza debe igualar la tasa neta de transporte de impulso lineal fuera del sistema por flujo másico.
Sistema cerrado:
Un sistema con límites seleccionados para que el caudal másico en cualquier límite sea idéntico cero es un sistema cerrado; así la masa del sistema es constante. Cuando se aplica a la conservación del impulso lineal, esta suposición tiene el siguiente efecto:
\[ \begin{align*} \frac{d \cancel{ \mathbf{P}_{\text{sys}} }^{= m_{\text{sys}} \mathbf{V}_G} }{dt} &= \sum \mathbf{F}_{\text{ext}} + \sum_{\text{in}} \cancel{ \dot{m}_i }^{=0} \mathbf{V}_i - \sum_{\text{out}} \cancel{ \dot{m}_e }^{=0} \mathbf{V}_e \\ m_{\text{sys}} \frac{d \mathbf{V}_G}{dt} + \underbrace{ \cancel{ \frac{d m_{\text{sys}}}{dt} }^{=0} }_{\begin{array}{c} \text{Closed} \\ \text{system} \end{array} } \mathbf{V}_G &= \sum \mathbf{F}_{\text{ext}} \\ m_{\text{sys}} \frac{d \mathbf{V}_G}{dt} &= \sum \mathbf{F}_{\text{ext}} \end{align*} \nonumber \]
donde\(\mathbf{V}_{G}\) es la velocidad del centro de masa del sistema. Recordando que la aceleración es solo la derivada temporal de la velocidad, inmediatamente reconocemos que este es nuestro viejo amigo de la física:\(F=m a\).
Sistema cerrado de estado estacionario:
Usando lo que has aprendido hasta este punto, ¿cómo esperarías que la ecuación de impulso lineal se simplificara para un sistema cerrado que opera en condiciones de estado estacionario?
Al aplicar la conservación del impulso lineal para modelar un sistema, necesitaremos, como siempre, seleccionar un sistema e identificar los transportes de impulso lineal a través del límite del sistema. Las pautas para dibujar un diagrama de momento lineal (o cuerpo libre) se encuentran a continuación:
- Seleccione un sistema. Cada sistema se puede dividir en subsistemas más pequeños. Para un problema dado, puede haber varios sistemas posibles y diferentes preguntas pueden requerir un sistema diferente.
- Dibuje el objeto físico identificando claramente los límites de su sistema. Esto generalmente se hace con una línea discontinua para indicar el límite del sistema.
- Separe el sistema de su entorno y dibuje el contorno aislado del sistema, es decir, los límites del sistema.
- Identificar los transportes de impulso entre el sistema y el entorno. Al identificar fuerzas externas, sólo se consideran las fuerzas ejercidas por los alrededores sobre el sistema. Recuerde que existen dos tipos de fuerzas externas: las fuerzas de contacto (o superficiales) que actúan sobre los límites del sistema y las fuerzas corporales producidas por campos como la fuerza gravitacional comúnmente llamada peso.
- Para cada transporte de impulso, dibuje una flecha en el diagrama del sistema que muestre la dirección y ubicación del transporte. Se debe tener cuidado en dibujar cada flecha con la dirección correcta (línea de acción y sentido) y posición. Etiquetar todas las fuerzas y transportes masivos de impulso con un nombre, número o un símbolo. Dibuja el vector en el diagrama colocando la cola o la cabeza de la flecha en el punto de aplicación:
- Las fuerzas de contacto deben aplicarse en el punto apropiado en el límite del sistema donde el sistema fue “cortado” de los alrededores.
- El vector de peso se debe aplicar en el centro de gravedad del cuerpo.
- El transporte de masa del vector de momento lineal se debe aplicar en el punto donde la masa cruza el límite y en la dirección de la velocidad.
- Si no conoce la dirección correcta de una transferencia de impulso, asuma una dirección. Si su análisis da como resultado un valor numérico negativo para la transferencia, entonces la dirección real es opuesta a la dirección asumida.
- Dibuje un sistema de coordenadas e indique todas las dimensiones y ángulos pertinentes en el diagrama de cuerpo libre.
Un tenista sirve la pelota a una distancia\(L=40 \ \mathrm{ft}\) atrás de la red y una altura\(H=9 \ \mathrm{ft}\) por encima de la cancha. La pelota de tenis deja la raqueta con un ángulo\(\theta=0^{\circ}\) por debajo de la horizontal como se muestra en la figura. La red es\(3 \mathrm{ft}\) alta y el centro de la pelota de tenis despeja la red por 3 pulgadas. Determinar (a) la velocidad inicial\(V_{o}\) de la pelota cuando sale de la raqueta y (b) la distancia\(s\) detrás de la red donde la pelota golpea la cancha. Supongamos que el arrastre de aire es insignificante. La masa de la pelota de tenis es\(0.25 \ \mathrm{lbm}\).
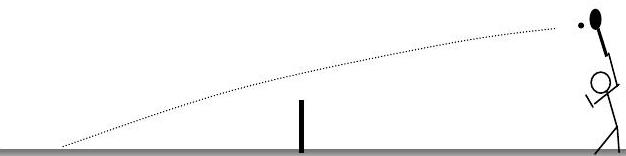
Figura\(\PageIndex{1}\): Un tenista sirve una pelota.
Solución
Conocido: La pelota de tenis se sirve con un ángulo específico desde una ubicación específica.
Encuentra: (a) La velocidad de la pelota cuando cruza la red y (b) la distancia de la red donde golpea la cancha.
Dado:
.jpg)
Figura\(\PageIndex{2}\): Diagrama que indica el camino recorrido por la pelota, asignado un sistema de coordenadas y etiquetado con todas las medidas relevantes.
Análisis:
Sistema\(\rightarrow\) Seleccione la pelota de tenis como sistema. Se trata de un sistema cerrado.
Propiedad a contar\(\rightarrow\) Dado que la trayectoria se rige por el efecto de la gravedad, cuente el momento lineal.
Período de tiempo Eventualmente\(\rightarrow\) necesitará integrarse en tiempo finito para obtener trayectoria y velocidad.
Primero debemos esbozar el diagrama de cuerpo libre (momento lineal) para el sistema. Los únicos transportes de impulso lineal ocurren debido a la fuerza del cuerpo gravitacional: el peso. El sistema de coordenadas inerciales y las demás dimensiones se muestran en la Figura\(\PageIndex{2}\) anterior.
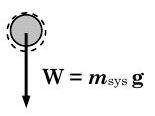.jpg)
Figura\(\PageIndex{3}\): Diagrama de cuerpo libre del sistema.
Escribir la forma de tasa de conservación del impulso lineal para el sistema da
\[ \frac{ d \mathbf{P}_{\text{sys}}}{dt} = \mathbf{W} + \underbrace{ \cancel{ \left[ \sum_{\text{in}} \dot{m}_i \mathbf{V}_i + \sum_{\text{out}} \dot{m}_e \mathbf{V}_e \right] }^{=0} }_{\text{Closed system, } \dot{m} = 0} \quad \rightarrow \quad \cancel{ \frac{d}{dt} \left( m_{\text{sys }} \mathbf{V}_G \right) }^{=m_{\text{sys}} \frac{d \mathbf{V}_G}{dt}} = m_{\text{sys }} \mathbf{g} \quad \rightarrow \quad m_{\text{sys }} \frac{d \mathbf{V}_G}{dt} = m_{\text{sys }} \mathbf{g} \nonumber \]
Ahora escribiendo la ecuación en forma escalar usando el sistema de coordenadas definido anteriormente y\(\mathbf{V}_G = V_x \mathbf{i} + V_y \mathbf{j}\), tenemos las siguientes ecuaciones:
\[ \cancel{ m_{\text{sys }} } \frac{d \mathbf{V}_G}{dt} = \cancel{ m_{\text{sys }} } \mathbf{g} \quad \rightarrow \quad \frac{d}{dt} \left( V_x \mathbf{i} + V_y \mathbf{j} \right) = -g \mathbf{j} \quad \rightarrow \quad \left\{ \begin{array}{l} x \text {- axis: } \quad \dfrac{d V_{x}}{d t}=0 \\ y \text {-axis: } \quad \dfrac{d V_{y}}{d t}=-g \end{array} \right. \nonumber \]
Integrar una vez para obtener velocidad da\[\begin{array}{llllll} x \text {-axis: } & \dfrac{d V_{x}}{d t} = 0 & \rightarrow & V_{x} = \text{constant} = V_{x, o} = V_{o}(\cos \theta) & \rightarrow & V_{x} = V_{o} (\cos \theta) \\ y \text {-axis: } & \dfrac{d V_{y}}{d t} = -g & \rightarrow & \int\limits_{V_{y, o}}^{V_{y}} d V_{y} = -\int\limits_{0}^{t} g \ dt \rightarrow V_{y} - V_{o} (\sin \theta) = -g t & \rightarrow & V_{y} = -g t+V_{o}(\sin \theta) \end{array} \nonumber \]
Ahora integrando de nuevo para obtener posición:\[\begin{array}{lllll} x \text {-axis: } & V_{x} = \dfrac{d x}{d t} = V_{o} \cos \theta & \rightarrow & \int\limits_{0}^{x} d x = \int\limits_{0}^{t} \underbrace{ \left(V_{o} \cos \theta\right) }_{\text{Constant}} \ dt & \rightarrow \quad x = \left(V_{o} \cos \theta\right) t \\ y \text {- axis: } & V_{y} = \frac{d y}{d t} = -gt - V_{o} \sin \theta & \rightarrow & \int\limits_{H}^{y} d x = -\int\limits_{0}^{t} \left(gt+V_{o} \sin \theta\right) \ d t & \rightarrow \quad y-H = -\left(\dfrac{g t^2}{2} + \left(V_{o} \sin \theta \right) t \right) \end{array} \nonumber \]
Ahora que conocemos la posición y la velocidad en función del tiempo, primero resolvamos la velocidad inicial requerida para despejar la red en\(x=L\) y\(y=h+d\).
Para\(\theta=0\) con\(x\) y\(y\) como se especificó anteriormente, tenemos dos ecuaciones para dos incógnitas\(t\) y\(V_{o}\):\[\begin{aligned} &x \text {-axis: } \quad\quad\quad\quad\quad\ L = V_{o} t & \rightarrow \quad & \ t =L / V_{o} \\ &y \text {-axis: } \quad (h+d)-H = -\left[\frac{1}{2} g t^{2}\right] & \rightarrow \quad & t^{2} =\frac{2}{g} [H-(h+d)] \end{aligned} \nonumber \]
Combinar estas ecuaciones y eliminar el tiempo\(t\) da el siguiente resultado:
\[\begin{gathered} t^{2} = \left( \frac{L}{V_{o}} \right)^{2} = \frac{2}{g}[H-(h+d)] \\ V_{o}^{2} = \frac{g L^{2}}{2[H-(h+d)]} \end{gathered} \quad \rightarrow \quad V_{o} = \sqrt{ \frac{g L^{2}}{2[H-(h+d)]} } = \sqrt{ \frac{ \left(32.2 \ \dfrac{\mathrm{ft}}{\mathrm{s}^{2}} \right)(40 \ \mathrm{ft})^{2}}{2 \left[ 9-\left( 3+\frac{3}{12} \right) \right] \mathrm{ft}}} = 66.9 \ \frac{\mathrm{ft}}{\mathrm{s}} \nonumber \]
Ahora para resolver\(s\), reconocemos que\(s = x - 40\) cuando\(y=0\) y usar las dos ecuaciones de desplazamiento:\[\begin{gathered} s = x-(40 \ \mathrm{ft}) = V_{o} t-(40 \ \mathrm{ft}) \\ 0-H = -\frac{1}{2} g t^{2} \quad \rightarrow \quad H=\frac{1}{2} g t^{2} \end{gathered} \quad \rightarrow \quad s=V_{o} \sqrt{\frac{2 H}{g}-(40 \ \mathrm{ft})} \nonumber \]
Resolviendo para la distancia\(s\):\(\quad s = \left( 66.9 \ \dfrac{\mathrm{ft}}{\mathrm{s}}\right) \sqrt{2 \dfrac{(9 \ \mathrm{ft})}{(32.3 \ \mathrm{ft} / \mathrm{s})}} - (40 \ \mathrm{ft}) = 10.0 \ \mathrm{ft}\)
Comentarios:
- Suponiendo que el diámetro de la pelota de tenis es de 3 pulgadas y los tenis aún golpean con la velocidad inicial calculada anteriormente, determinar el valor máximo de\(\theta\) antes de que la pelota golpee la red.
- Ahora determina la velocidad inicial mínima que debe tener la pelota para despejar la red si es golpeada horizontalmente, e.g\(\theta=0\).
El agua fluye constantemente a través de una boquilla horizontal unida a una tubería. La boquilla está bridada y unida a la tubería con 6 pernos como se muestra en la figura. La tubería y la entrada de la boquilla tienen un diámetro interior de\(25 \ \mathrm{cm}\) y el diámetro de salida de la boquilla es\(12 \ \mathrm{~cm}\). La presión absoluta en la entrada a la boquilla es\(500 \ \mathrm{kPa}\) y la velocidad del agua es\(5 \mathrm{~m} / \mathrm{s}\). La presión en la salida de la boquilla es la presión atmosférica\(\left(P_{\mathrm{atm}}= 100 \mathrm{kPa} \right) \). Supongamos que la densidad del agua líquida es\(1000 \mathrm{~kg} / \mathrm{m}^{3}\).
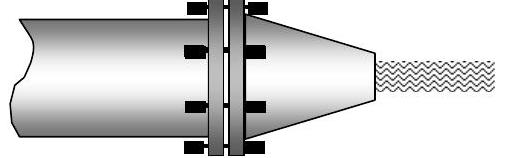
Figura\(\PageIndex{4}\): El agua se mueve a través de una tubería cilíndrica unida a una boquilla con brida.
Determinar la fuerza total, en newtons, aplicada por los pernos para mantener la boquilla en su lugar. Supongamos que los pernos solo soportan tensión.
Solución
Conocido: El agua fluye constantemente a través de una boquilla.
Encuentra: Encuentra la fuerza total ejercida por los pernos en la boquilla para sujetarla en su lugar.
Dado:
.jpg)
Figura\(\PageIndex{5}\): La tubería y la boquilla, asignadas con un sistema de coordenadas y etiquetadas con todas las cantidades dadas.
Análisis:
Estrategia: Intente el impulso lineal en la\(x\) dirección -ya que el problema pide fuerzas (un mecanismo para transferir impulso lineal) y las fuerzas están en la\(x\) dirección.
Sistema\(\rightarrow\) Elija un sistema abierto y no deformante que corte la tubería en la conexión de la boquilla de la tubería e incluya la boquilla.
Propiedad para contar\(\rightarrow\) Pruebe el impulso lineal y posiblemente la masa (si necesitamos relacionar los caudales de entrada con salida.
Período de tiempo\(\rightarrow\) Parece que puede ser un problema de tasa (intervalo de tiempo infinitesimal) o de estado estacionario.
.jpg)
Figura\(\PageIndex{6}\): Elección del sistema para este problema.
Comenzando con el sistema mostrado por la línea discontinua, identifique todas las transferencias de impulso para el sistema. Al caminar con los dedos alrededor del límite del sistema, identificaría seis fuerzas de cerrojo, fuerzas de presión y los dos transportes masivos de impulso. Ahora escribiéndolos en una ecuación vectorial para el impulso lineal en la\(x\) dirección -dirección, tenemos:\[ \frac{d \mathbf{P}_{x, \text{ sys}}}{dt} = \left[ 6 \mathbf{F}_{\text{bolt, } x} + \mathbf{F}_{\text {net pressure, } x} \right] + \left[ \dot{m} \mathbf{V}_{1, \ x} - \dot{m} \mathbf{V}_{2, \ x} \right] \nonumber \]
Ahora se requiere un diagrama de impulso más completo para obtener las direcciones correctas de las fuerzas. A continuación se muestra el diagrama completo.
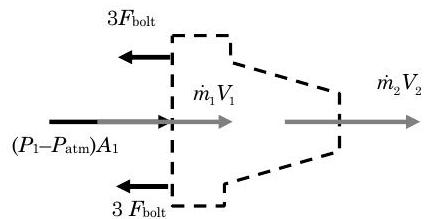.jpg)
Figura\(\PageIndex{7}\): Diagrama de cuerpo libre para el sistema de boquillas.
Antes de continuar, debemos explicar cómo obtuvimos los diversos términos.
- Los términos de transporte de masa son el producto del caudal másico y la velocidad en cualquier límite de flujo. La dirección de la flecha está en la dirección de la velocidad.
- Dos flechas muestran las fuerzas del cerrojo. Cada flecha representa tres (3) pernos. Además, solo se puede determinar la fuerza promedio del perno. Tenga en cuenta que como los pernos están en tensión, las flechas indican que los pernos están tirando del sistema.
- Las fuerzas netas de presión en la\(\mathrm{x}\) dirección deben calcularse considerando la distribución de presión en todo el límite del sistema. Como se muestra en la figura, la presión atmosférica\(P\) atm actúa sobre todas las superficies excepto el área de flujo de entrada donde está la presión\(P_{1}\). Observe que todas las flechas de presión apuntan hacia la superficie. La fuerza neta se puede determinar restando la presión atmosférica como se muestra en la figura. El resultado es una presión uniforme de\(P_{\text {net }}=P_{1}-P_{\text {atm }}\) actuar sobre el área de entrada. La magnitud de la fuerza resultante es\(F_{\text {net pressure, } x} = \left( P_1 - P_{\text {atm}} \right) A_{1}\). Esta flecha apunta hacia la superficie y se muestra en el diagrama de impulso anterior.
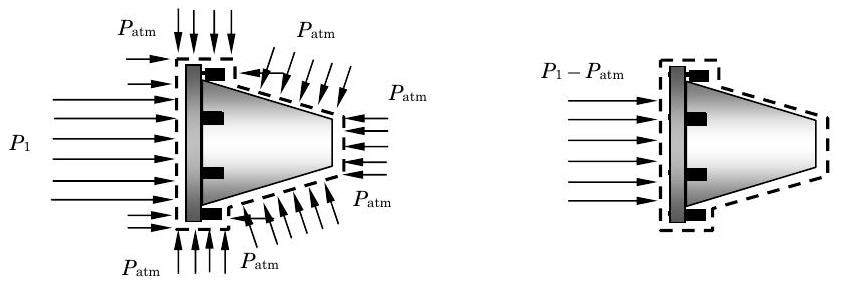
Figura\(\PageIndex{8}\): Métodos equivalentes de expresión de la presión neta experimentada por el sistema de boquillas.
Ahora todo lo que queda es resolver por las fuerzas del cerrojo. Escribiendo la ecuación de momentum como escalar para la\(\mathrm{x}-\) dirección que tenemos:
\[ \begin{align*} & \underbrace{ \cancel{ \frac{d P_{x, \text{ sys}}}{dt} }^{=0} }_{\text{Steady-state}} = \left[ -6 F_{\text{bolt, } x} + \underbrace{ F_{\text{net pressure, } x} }_{= \left( P_1 - P_{\text{atm}} \right) A_1} \right] + \underbrace{ \left[ \dot{m}_1 \left( + V_{1, \ x} \right) - \dot{m}_2 \left( + V_{2, \ x} \right) \right] }_{\begin{array}{c} + \text{ sign for each } V \text{ since a positive value} \\ \text{for } V_{1, \ x} \text{ and } V_{2, \ x} \text{ represents a positive} \\ \text{specific linear momentum} \end{array}} \\[4pt] & 0 = -6 F_{\text{bolt, } x} + \left( P_1 - P_{\text{atm}} \right) A_1 + [ \dot{m}_1 V_1 - \dot{m}_2 V_2 ] \quad \rightarrow \quad 6 F_{\text{bolt, } x} = \left( P_1 - P_{\text{atm}} \right) A_1 + [ \dot{m}_1 V_1 - \dot{m}_2 V_2 ] \end{align*} \nonumber \]
Se puede lograr una mayor simplificación aplicando la conservación de la masa al mismo sistema y luego aplicando el supuesto de estado estacionario:
\[ \cancel{ \frac{d m_{\text{sys}}}{d t} }^{=0} = \dot{m}_1 - \dot{m}_2 \quad \rightarrow \quad \dot{m}_2 = \dot{m}_1 \quad \rightarrow \quad \underbrace{ \cancel{ \rho_1 } A_1 V_1 = \cancel { \rho_2 } A_2 V_2 }_{\text {Incompressible liquid}} \nonumber \]
Usando este resultado, la ecuación para las fuerzas del perno se convierte en\[6 F_{\text {bolt}} = \left( P_{1}-P_{\text {atm}} \right) A_{1} + \dot{m}_{1} \left( V_{1}-V_{2}\right) \nonumber \]
Resolviendo para el área en la entrada:\(A_{1} = \frac{\pi}{4} D_{1}^{2} = \frac{\pi}{4} (0.25 \mathrm{~m})^{2} = 4.909 \times 10^{-2} \mathrm{~m}^{2}\)
Resolviendo para el caudal másico:\(\dot{m}_{1} = \rho A_{1} V_{1} = \left( 1000 \ \frac{\mathrm{kg}}{\mathrm{m}^{3}} \right) \left( 4.909 \times 10^{-2} \mathrm{~m}^{2} \right) \left( 5 \ \frac{\mathrm{m}}{\mathrm{s}}\right) = 245.5 \ \frac{\mathrm{kg}}{\mathrm{s}}\)
La velocidad en la salida se convierte en:\(V_{2} = \dfrac{A_1}{A_2} V_{1} = \left[ \dfrac{(\pi / 4) D_{1}^{\ 2}}{(\pi / 4) D_{2}^{\ 2}} \right] V_{1} = \left( \dfrac{D_1}{D_2} \right)^{2} V_{1} = \left( \dfrac{25 \mathrm{~cm}}{12 \mathrm{~cm}}\right)^{2} \left( 5 \dfrac{\mathrm{m}}{\mathrm{s}} \right) = 21.70 \ \dfrac{\mathrm{m}}{\mathrm{s}}\)
Sustituir estos números de nuevo en el resultado general da\[\begin{aligned} 6 F_{\text {bolt}} &= \left( P_{1} - P_{\text {atm}} \right) A_{1} + \dot{m}_{1} \left( V_{1} - V_{2} \right) \\ &=[(500-100) \ \mathrm{kPa}] \left( 4.904 \times 10^{-2} \mathrm{~m}^{2} \right) + \left( 245.5 \ \frac{\mathrm{kg}}{\mathrm{s}} \right) (5.00-21.70) \frac{\mathrm{m}}{\mathrm{s}} \\ &=\left( 19.64 \ \mathrm{kPa} \cdot \mathrm{m}^{2} \right) \left( \frac{1000 \mathrm{~N} / \mathrm{m}^{2}}{\mathrm{kPa}} \right) + \left( -4100 \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}^{2}} \right) \left( \frac{\mathrm{N}}{\left( \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}^{2}} \right)} \right) \\ &=19.64 \times 10^{3} \mathrm{~N} + \left( -4.10 \times 10^{3} \mathrm{~N} \right) \\ &=15.5 \ \mathrm{kN} \end{aligned} \nonumber \]
Así, los seis pernos deben ejercer una fuerza total de\(15.5 \ \mathrm{kN}\) actuación hacia la izquierda (o hacia la tubería) para mantener la boquilla en su lugar.
Comentarios:
- Tenga en cuenta que el incremento en el momento lineal específico, es decir\(V\), de la masa que sale del sistema realmente sirve para reducir la carga sobre los pernos. Para ver esto, considera cuál sería la fuerza del perno si la boquilla estuviera tapada.
- ¿Cómo cambiaría la solución si hubiéramos elegido la\(x\) coordenada básica a la izquierda en lugar de a la derecha como se muestra? La relación vectorial habría permanecido igual, pero la ecuación escalar se habría convertido en la siguiente
\[ 0 = 6 F_{\text {bolt, }x} - \left(P_{1} - P_{\text {atm}}\right) A_{1} + \left[ \dot{m}_{1} \left( -V_{1} \right) - \dot{m}_{2} \left(-V_{2}\right) \right] \quad \rightarrow \quad 6 F_{\text {bolt, } x} = \left( P_{1} - P_{\text {atm}} \right) A_{1} + \left[ \dot{m}_{1} \left(V_{1}\right) - \dot{m}_{2} \left(V_{2}\right) \right] \nonumber \]
Un teleférico es tirado a lo largo de un cable aéreo fijo por un cable conectado en un punto\(A\). El carro tiene una masa de\(200 \ \mathrm{kg}\), y la tensión en el cable es\(2400 \ \text{N}\). El carro está soportado por ruedas que descansan sobre el cable. El cable está inclinado en ángulo\(\theta=22.6^{\circ}\) con la horizontal como se muestra en la figura.
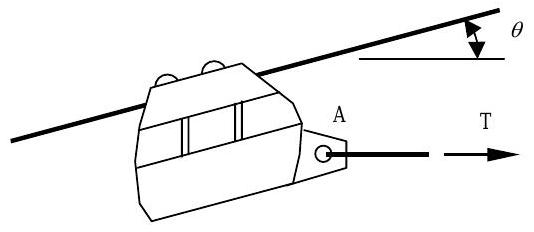
Figura\(\PageIndex{9}\): El teleférico suspendido de un cable en ángulo es tirado hacia la derecha por un cable horizontal.
Determinar:
a) La magnitud y dirección de la fuerza\(R\) ejercida por el cable aéreo sobre las ruedas del automóvil, en newtons.
b) La magnitud y dirección de la aceleración del automóvil en\(\mathrm{m} / \mathrm{s}^{2}\).
Solución
Conocido: Un pequeño vagón de inspección es arrastrado a lo largo de un cable aéreo fijo por un cable conectado en el punto\(A\)
Encuentra: a) La magnitud y dirección de la fuerza\(R\) ejercida por el cable aéreo sobre las ruedas del automóvil, en newtons. b) La magnitud y dirección de la aceleración del automóvil, en\(\mathrm{m} / \mathrm{s}^{2}\).
Dado:
\[\begin{aligned} &\mathrm{T} = 2400 \mathrm{~N} \\ & m_{\mathrm{car}}=200 \mathrm{~kg} \\ & \theta = 22.6^{\circ} \end{aligned} \nonumber \]
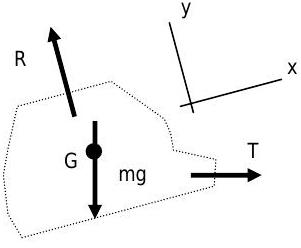.jpg)
Figura\(\PageIndex{10}\): Diagrama de cuerpo libre del teleférico aislado.
Análisis:
Estrategia\(\rightarrow\) Dado que el problema involucra fuerzas, intente conservar el impulso lineal.
Sistema Sistema\(\rightarrow\) cerrado que incluye solo el automóvil como se muestra en el diagrama del sistema de impulso a la derecha.
Propiedad\(\rightarrow\) Lineal Momento Período de
Tiempo\(\rightarrow\) Instantáneo
Sin seleccionar un sistema de coordenadas, la conservación de la ecuación de impulso lineal se convierte en\[\frac{d}{d t} \mathbf{P}_{\mathrm{sys}}=\sum_{\text {external}} \mathbf{F}_{j} + \sum_{\mathrm{in}} \cancel{ \dot{m}_{i} \mathbf{V}_{i} }^{=0} - \sum_{\text{out}} \cancel{ \dot{m}_{e} \mathbf{V}_{e} }^{=0, \text { closed system}} \quad \rightarrow \quad \frac{d}{d t} \mathbf{P}_{\mathrm{sys}} = m_{\mathrm{sys }} \mathbf{g} + \mathbf{T} + \mathbf{R} \nonumber \] donde solo hay tres fuerzas externas: la fuerza sobre las ruedas\(\mathbf{R}\), el peso del automóvil\(m_{\mathrm{sys }} \mathbf{g}\) y la fuerza del cable\(\mathbf{T}\). La fuerza de presión neta es cero ya que la presión atmosférica rodea al automóvil.
También, debido a que se trata de un sistema cerrado el momento lineal del sistema\(\mathbf{P}_{\text {sys}} = m_{\text {sys}} \mathbf{V}_{G}\) donde\(\mathbf{V}_{G}\) está la velocidad del centro de masa del sistema. Así, la conservación del momento lineal ahora se puede escribir como\[\frac{d}{dt} \left( m_{\text{sys }} \mathbf{V}_{\mathrm{G}}\right) = m_{\text{sys }} \mathbf{g} + \mathbf{T} + \mathbf{R} \quad \rightarrow \quad m_{\text{sys }} \frac{d \mathbf{V}_{\mathrm{G}}}{dt} = m_{\text{sys }} \mathbf{g} + \mathbf{T} + \mathbf{R} \nonumber \] Ahora seleccionando un sistema de coordenadas que esté alineado con el cable, la conservación del momento lineal se puede escribir en dos componentes. En la\(y\) dirección, la ecuación de impulso lineal se convierte en
\[ m_{\text{sys }} \cancel{ \frac{d V_{G, \ y}}{dt} }^{ \begin{array}{l} =0; \text{ no motion} \\ \text{in } y \text{-direction} \end{array}} = -\left( T \cdot \sin \theta \right) + R - \left( m_{\text{sys }} g \cdot \cos \theta \right) \quad \rightarrow \quad R = \left( T \cdot \sin \theta \right) + \left( m_{\text{sys }} g \cdot \cos \theta \right) \nonumber \]
después de resolver por la fuerza\(R\).
Sustituir en la información numérica da\[\begin{aligned} R &= (2400 \mathrm{~N}) \cdot \sin \left( 22.6^{\circ} \right) + (200 \mathrm{~kg}) \left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \cdot \cos \left( 22.6^{\circ} \right) \\ &= \quad\quad\quad 922.3 \mathrm{~N} \ \ \quad\quad + \quad\quad\quad 1811 \mathrm{~N} \quad\quad\quad\quad\quad\quad\quad = 2733 \mathrm{~N} \end{aligned} \nonumber \]
En la\(x\) dirección, la ecuación de impulso lineal se convierte en\[\begin{aligned} m_{\mathrm{sys}} \frac{d V_{\mathrm{G}, \ x}}{d t} &= (T \cdot \cos \theta) - \left(m_{\text{sys }} g \cdot \sin \theta\right) \\[4pt] \frac{d V_{\mathrm{G}, \ x}}{d t} &= \dfrac{(T \cdot \cos \theta) - \left(m_{\text{sys }} g \cdot \sin \theta\right)}{m_{\mathrm{sys}}}=\left(\frac{T}{m_{\mathrm{sys}}} \cos \theta\right)-(g \cdot \sin \theta) \end{aligned} \nonumber \]
Recordando la definición de aceleración, la ecuación\(\mathrm{x}\) -momentum se puede resolver para la aceleración como\[a_{\mathrm{G}, \ x} \equiv \frac{d V_{\mathrm{G}, \ x}}{dt} = \left(\frac{T}{m_{\mathrm{sys}}} \cos \theta \right) - (g \cdot \sin \theta) \nonumber \] Sustituir en la información numérica da\[\begin{aligned} a_{\mathrm{G}, \ x} &= \left(\frac{2400 \mathrm{~N}}{200 \mathrm{~kg}}\right) \cos \left(22.6^{\circ}\right) - \left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \sin \left(22.6^{\circ}\right) = \left(12.0 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)(0.9232)-\left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)(0.3843) \\[4pt] &=7.31 \ \frac{\mathrm{m}}{\mathrm{s}^{2}} \end{aligned} \nonumber \]
Comentarios:
- Como parte de un estudio de seguridad, determinar cómo cambiarían la fuerza\(R\) y la aceleración del automóvil si el cable de tracción se rompiera repentinamente.
- Después de una falla del cable de tracción, la velocidad máxima del teleférico se limita a un mecanismo\(15 \mathrm{~m} / \mathrm{s}\) de frenado de emergencia en el carro de ruedas. La fuerza de frenado se activa cuando alcanza la velocidad de un automóvil que “cae”\(5 \mathrm{~m} / \mathrm{s}\). ¿Qué fuerza de frenado se debe ejercer sobre el teleférico para limitar la velocidad del automóvil? Si el automóvil está parado cuando se rompe el cable de tracción, ¿cuánto tiempo tardará en activarse el freno de emergencia y cuándo se alcanzará la velocidad máxima?
Se utiliza una báscula para pesar el agua en un tanque. El agua fluye de manera constante a través del tanque como se muestra en la figura. Entra por la parte superior del tanque con caudal volumétrico de\(30 \mathrm{~m}^{3} / \mathrm{s}\) a través de una tubería con un diámetro de\(6 \mathrm{~cm}\). Sale al costado del tanque a través de una abertura circular con un\(6 \mathrm{-cm}\) diámetro. El volumen del agua en el tanque es\(0.6 \mathrm{~m}^{3}\), y el peso seco del tanque es\(500 \mathrm{~N}\). Determinar la lectura de la escala, en newtons.
.png)
Figura\(\PageIndex{11}\): El agua ingresa a un tanque en una báscula a través de la abertura 1 y sale del tanque por la abertura 2.
Solución
Conocido: El agua fluye de manera constante a través de un tanque que descansa sobre una balanza.
Encuentra: La lectura de la escala.
Dado:
Tubo de entrada @ 1
Caudal volumétrico\(\dot{V\kern-0.8em\raise0.3ex-}_{1}=30 \mathrm{~m}^{3} / \mathrm{h}\)
Diámetro\(D_{1}=6 \mathrm{~cm}\)
Abertura de Salida @ 2
Diametro\(D_{2}=6 \mathrm{~cm}\)
Volumen de agua en el tanque en estado estacionario:\(V\kern-1.0em\raise0.3ex-_{\text {water}}=0.6 \mathrm{~m}^{3}\)
Peso del tanque:\(W_{\text {tank}}=500 \mathrm{~N}\)
Análisis:
Estrategia\(\rightarrow\) Dado que el problema involucra fuerzas, intente conservar el impulso lineal.
Sistema Sistema\(\rightarrow\) abierto que incluye toda el agua en el tanque y el tanque como se muestra en el diagrama del sistema de impulso.
Propiedad para contar Momento\(\rightarrow\) lineal y masa Periodo de
tiempo\(\rightarrow\) Instantáneo
.jpg)
Figura\(\PageIndex{12}\): Diagrama de cuerpo libre del sistema que consiste en el tanque y el agua que contiene.
Escribir la forma de tasa de la ecuación de conservación de impulso lineal para este problema da
\[ \begin{align*} \frac{d \mathbf{P}_{\text {sys}}}{d t} &= \sum_{\text {external}} \mathbf{F}_{j} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \\ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{\mathrm{s}} }^{\begin{array}{l} =0 \\ \text {steady state} \end{array}} &= \left(\mathbf{W}_{\text {tank}} + \mathbf{W}_{\text {water}} \right) + \mathbf{F}_{\text {scale}} + \dot{m}_{1} \mathbf{V}_{1} -\dot{m}_{2} \mathbf{V}_{2} \mathrm{~A} \\ 0 &= \left( \mathbf{W}_{\text{tank}} +\mathbf{W}_{\text{water}} \right) + \mathbf{F}_{\text {scale}} +\dot{m}_{1} \mathbf{V}_{1} - \dot{m}_{2} \mathbf{V}_{2} \end{align*} \nonumber \]
Ahora escribiendo el componente de esta ecuación en la dirección y como se define en la figura anterior,\[0 = \left[ W_{\text {tank}} + W_{\text {water}} \right] -F_{\text {scale}} + \dot{m}_{1} V_{1, y} - \dot{m}_{2} \cancel{ V_{2, y} }^{\begin{array}{l} =0 \\ \text{No } y \text{-component @ 2} \end{array}} \nonumber \]
Resolviendo para\(F_{\text {scale}}\) tenemos\[F_{\text {scale}} = W_{\text {tank}} + W_{\text {water}} + \dot{m}_{1} V_{1, y} \nonumber \]
Ahora resolviendo por el peso del tanque\(W_{\text {tank}}\) tenemos\[W_{\text {water}} = m_{\text {water }} g = \left( \rho_{\text {water}} V_{\text {water}} \right) g = \left(1000 \ \frac{\mathrm{kg}}{\mathrm{m}^{3}} \right) \left( 0.600 \mathrm{~m}^{3} \right) \left( 9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) = 5886 \mathrm{~N} \nonumber \]
El\(\mathrm{y}\) -componente de la velocidad a 1 y el caudal másico en 1 son
\[\begin{align*} V_{1, y} = V_{1}=\frac{\dot{V\kern-0.8em\raise0.3ex-}_{1}}{A_{1}} = \frac{\dot{V\kern-0.8em\raise0.3ex-}_{1}}{\left( \dfrac{\pi}{4} D_{1}^{\ 2}\right)} = \frac{\left(30 \ \dfrac{\mathrm{m}^{3}}{\mathrm{h}} \times \dfrac{1 \mathrm{~h}}{3600 \mathrm{~s}} \right)}{\dfrac{\pi}{4} (0.06 \mathrm{~m})^{2}} = 2.95 \ \frac{\mathrm{m}}{\mathrm{s}} \\[4pt] \dot{m}_{1}=\rho_{1} \dot{V\kern-0.8em\raise0.3ex-}_{1} = \left(1000 \ \frac{\mathrm{kg}}{\mathrm{m}^{3}}\right) \left( 30 \ \frac{\mathrm{m}^{3}}{\mathrm{h}} \times \frac{1 \mathrm{~h}}{3600 \mathrm{~s}}\right) = 8.33 \ \frac{\mathrm{kg}}{\mathrm{s}} \end{align*} \nonumber \]
Combinando esto para resolver la fuerza de la báscula en el tanque,\(F_{\text {scale}}\):\[\begin{aligned} F_{\text {scale}} &=W_{\text {tank }} + W_{\text {water }} + \dot{m}_{1} V_{1, y} \\ &=(500 \mathrm{~N}) + (5886 \mathrm{~N}) + \left(8.33 \ \frac{\mathrm{kg}}{\mathrm{s}}\right) \left(2.95 \ \frac{\mathrm{m}}{\mathrm{s}}\right) \\ &= (6386 \mathrm{~N}) + (24.6 \mathrm{~N}) \\ &=6411 \mathrm{~N} \end{aligned} \nonumber \]
Si el operador hubiera descuidado el efecto del agua que fluye hacia el tanque en la lectura, habría sobreestimado la cantidad de agua en el tanque aproximadamente\(0.4 \%\).
Comentario:
¿Cuál es la magnitud y dirección de la fuerza horizontal que la báscula debe ejercer sobre el tanque para evitar que se deslice fuera de la plataforma? [Respuesta:\(24.6 \mathrm{~N} \leftarrow\)] ¿Cómo podría usar una medición de fuerza lateral para indicar el caudal?


