5.5: Momentum lineal revisitado

En esta sección se consideran aspectos adicionales del cálculo del impulso lineal. La primera subsección considera el uso de velocidades relativas y la segunda subsección aborda el uso de coordenadas cilíndricas para describir el movimiento plano curvilíneo.

Uso de Velocidades Relativas

El siguiente ejemplo ilustra cómo se puede utilizar la conservación del impulso lineal para resolver el movimiento de un cohete que se está acelerando. Este ejemplo hace uso de velocidades relativas.

Ejemplo: un cohete de aceleración

Un pequeño cohete completamente cargado con combustible y oxidante tiene una masa de\(500 \ \mathrm{Mg}\), y\(80 \%\) de la masa total es combustible y oxidante. El cohete apunta verticalmente hacia arriba y se coloca sobre una plataforma de lanzamiento en la superficie de la Tierra. Después del encendido, el caudal másico del escape del motor del cohete es\(2300 \mathrm{~kg} / \mathrm{s}\) con una velocidad de salida\(2100 \mathrm{~m} / \mathrm{s}\) relativa al cohete. Descuidando las fuerzas de presión y el arrastre del fluido, determine (a) ¿cuánto tiempo después de la ignición ocurre el agotamiento (es decir, el cohete se queda sin combustible y oxidante)? (b) ¿cuánto tiempo después de la ignición ocurre el despegue? y c) ¿cuál es la velocidad del cohete al quemarse?

Solución

Conocido: Un pequeño cohete despega de la superficie de la tierra.

Encontrar: (a) tiempo después de la ignición hasta el agotamiento; (b) tiempo después del encendido hasta el despegue; (c) velocidad del cohete al quemarse.

Dado:

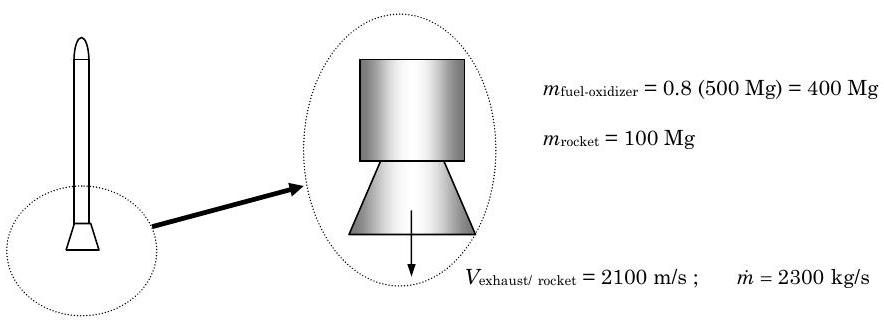
Figura\(\PageIndex{1}\): Información dada.

Análisis:

Estrategia\(\rightarrow\) Ya que nos preocupa la velocidad de un objeto acelerante y por el tiempo necesario para quedarse sin la masa de combustible y oxidante, intentemos usar masa e impulso lineal.
Sistema\(\rightarrow\) Tome un sistema abierto, no deformante que incluya el cohete con masa cruzando el límite en el escape.
Propiedad a contar\(\rightarrow\) Como se indicó anteriormente, pruebe la masa y el impulso lineal.
Intervalo de tiempo\(\rightarrow\) Comience con la forma de tasa y luego vea lo que se necesita.

Figura\(\PageIndex{2}\): Elección del sistema y dirección del flujo másico a través del límite.

Para el sistema anterior, la masa fluye fuera del fondo del cohete como lo indica la flecha. Para resolver la parte (a), escribir la conservación de la masa para el sistema; luego integrándonos con el tiempo, tenemos:\[\begin{align*} \frac{d m_{\text{sys}}}{dt} = -\dot{m}_{e} \quad & \rightarrow \quad \int\limits_{t_{1}}^{t_{2}} \left(\frac{d m_{\text{sys}}}{dt}\right) dt = \int\limits_{t_{1}}^{t_{2}} \left(-\dot{m}_{e}\right) dt \quad \rightarrow \quad m - m_{o} = -\dot{m}_{e} t \\ m = m_{o} - \dot{m}_{e} t \quad & \rightarrow \quad m=(500,000 \mathrm{~kg}) - \left( 2300 \ \frac{\mathrm{kg}}{\mathrm{s}}\right) t \end{align*} \nonumber \]

Observe que el caudal másico se calcula con respecto al escape del cohete. En el agotamiento, la masa del sistema equivale solo a la masa del cohete vacío:\[t_{\text {burnout}} = \frac{(500,000 \mathrm{~kg} - 100,000 \mathrm{~kg})}{\left(2300 \ \dfrac{\mathrm{kg}}{\mathrm{s}}\right)} = 173.9 \text { seconds } \nonumber \]

Ahora para resolver el tiempo de despegue, necesitamos aplicar la conservación del impulso lineal:\[ \begin{align*} \boxed{ \uparrow + } \quad\quad\quad\quad\quad\quad\quad\quad \frac{d P_{y, \ \text{sys}}}{dt} &= -mg - \dot{m}_e V_{y, \ e} \\[4pt] \frac{d \left( m V_G \right)}{dt} &= -mg - \dot{m}_e \underbrace{ \left( V_G - V_{\text{exhaust / rocket}} \right) }_{\begin{array}{c} \text{Absolute velocity of the exhaust} \\ \text{with respect to the ground} \end{array}} \\ m \frac{d V_G}{dt} + V_G \underbrace{ \cancel{ \frac{dm}{dt} }^{= - \dot{m}_e} }_{\begin{array}{c} \text{Using conservation} \\ \text{of mass results} \end{array}} &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) \\ m \frac{d V_G}{dt} + V_G \left( - \dot{m}_e \right) &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) \\ m \frac{d V_G}{dt} &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) + \dot{m}_e V_G \\[4pt] m \frac{d V_G}{dt} &= -mg - \cancel{ \dot{m}_e V_G } + \dot{m}_e V_{\text{exhaust / rocket}} + \cancel{ \dot{m}_e V_G } \\[8pt] m \frac{d V_G}{dt} &= -mg + \dot{m}_e V_{\text{exhaust / rocket}} \end{align*} \nonumber \]

Estudie cuidadosamente los pasos anteriores. Tenga en cuenta que debe tener cuidado de usar la velocidad absoluta del escape que sale del escape. También hay que señalar que hacemos uso de la ecuación de conservación de masa para simplificar la conservación del impulso lineal.

Para resolver para la parte (b), el tiempo de despegue, podemos usar la ecuación anterior. Al despegar la aceleración del sistema es cero, ya que el empuje apenas equilibra el peso de la gravedad:\[m \cancel{ \frac{d V_G}{d t} }^{=0} = -mg + \dot{m}_{e} V_{\text {exhaust / rocket }} \quad \rightarrow \quad \begin{gathered} mg = \dot{m}_{e} V_{\text {exhaust / rocket}} \\ \left(m_{o}-\dot{m}_{e} t \right) g = \dot{m}_{e} V_{\text {exhaust / rocket}} \\ m_{o} g = \dot{m}_{e} \left(gt + V_{\text {exhaust / rocket}}\right) \end{gathered} \quad \rightarrow \quad t_{\text {liftoff}} = \frac{m_{o}}{\dot{m}_{e}} - \frac{V_{\text {exhaust / rocket}}}{g} \nonumber \]

Luego resolviendo para el tiempo de despegue:\[t_{\text {liftoff}} = \frac{m_{o}}{\dot{m}_{e}} - \frac{V_{\text {exhaust / rocket}}}{g} = \left(\frac{500,000 \mathrm{~kg}}{2300 \mathrm{~kg} / \mathrm{s}}\right) - \left(\frac{2100 \mathrm{~m} / \mathrm{s}}{9.81 \mathrm{~m} / \mathrm{s}^{2}} \right) = 3.32 \mathrm{~seconds} \nonumber \]

Finalmente para resolver la velocidad en el burnout, debemos calcular la velocidad del cohete en función del tiempo. Esto lo hacemos integrando la ecuación de aceleración para el cohete. Primero reordenando la conservación del resultado de impulso lineal, tenemos una expresión para la aceleración del cohete:\[\frac{d V_{G}}{d t} = -g + \frac{\dot{m}_{e}}{m} V_{\text {exhaust / rocket }} \nonumber \]

Integrar esto con el tiempo desde el punto de despegue da lo siguiente:\[ \begin{align*} \int\limits_{t_{\text{liftoff}}}^{t} \left( \frac{d V_G}{dt} \right) dt &= \int\limits_{t_{\text{liftoff}}}^{t} \left[ -g + \frac{\dot{m}_e V_{\text{exhaust / rocket}}}{\left( m_o - \dot{m}_e t \right)} \right] dt \\[4pt] \left. V_G - V_G \right|_{t_{\text{liftoff}}} &= \int\limits_{t_{\text{liftoff}}}^{t} \left[ -g \right] dt + \int\limits_{t_{\text{liftoff}}}^{t} \left[ \frac{\dot{m}_e V_{\text{exhaust / rocket}}}{\left( m_o - \dot{m}_e t \right)} \right] dt \\[4pt] V_G - \cancel{ \left. V_G \right|_{t_{\text{liftoff}}} }^{=0} &= -g \left( t - t_{\text{liftoff}} \right) + \dot{m}_e V_{\text{exhaust / rocket}} \left[ \frac{1}{\dot{m}_e} \int\limits_{t_{\text{liftoff}}}^{t} \frac{\dot{m}_e \ dt}{\left( m_o - \dot{m}_e t \right) } \right] \\[4pt] V_G &= -g \left( t - t_{\text{liftoff}} \right) + \dot{m}_e V_{\text{exhaust / rocket}} \left[ - \frac{1}{\dot{m}_e} \ \ln \left( \frac{m_o - \dot{m}_e t}{m_o - \dot{m}_e t_{\text{liftoff}}} \right) \right] \\[10pt] V_G &= -g \left( t - t_{\text{liftoff}} \right) - V_{\text{exhaust / rocket}} \left[ \ln \left( \frac{m_o - \dot{m}_e t}{m_o - \dot{m}_e t_{\text{liftoff}}} \right) \right] \end{align*} \nonumber \]

Tenga en cuenta que esta ecuación sólo es válida para\(t_{\text {liftoff}} \leq t \leq t_{\text {burnout}}\). Resolviendo para la velocidad en burnout da\[\begin{aligned} V_{G} &= -g \left(t_{\text {burnout}} - t_{\text {liftoff}}\right) - V_{\text {exhaust / rocket}} \left[\ln \left(\frac{m_{o}-\dot{m}_{e} t_{\text {burnout}}}{m_{o}-\dot{m}_{e} t_{\text {liftoff}}}\right)\right] \\[4pt] &= -\left(9.81 \ \frac{\mathrm{kg}}{\mathrm{s}}\right)(173.9-3.32) \mathrm{s}-\left(2100 \ \frac{\mathrm{m}}{\mathrm{s}}\right) \left[\ln \frac{(100 \ \mathrm{Mg})}{\left(500 \ \mathrm{Mg}-2.3 \ \dfrac{\mathrm{Mg}}{\mathrm{s}}(3.32 \mathrm{~s})\right)}\right] \\[4pt] &=\left(-1673 \ \frac{\mathrm{m}}{\mathrm{s}}\right) - \left(-3348 \ \frac{\mathrm{m}}{\mathrm{s}}\right) \\[4pt] &= 1675 \mathrm{~m} / \mathrm{s} \end{aligned} \nonumber \]

Comentarios

¿Qué tan alto de la tierra estaría el cohete en el agotamiento? ¿Cómo podrías calcular esto? ¿Crees que nuestro modelo es preciso hasta el agotamiento? ¿Qué posibles problemas verías?

Si el diámetro del escape de la boquilla del cohete es\(5 \mathrm{~m}\) y la presión de escape es\(10 \ \mathrm{kPa}\), determine la fuerza de presión neta en el sistema. Supongamos que la presión atmosférica es\(100 \ \mathrm{kPa}\). ¿Descuidar la fuerza de presión era razonable?

Movimiento con coordenadas cilíndricas

La siguiente aplicación muestra cómo se pueden usar coordenadas cilíndricas para describir el movimiento curvilíneo plano.

Aplicación — Movimiento curvilíneo plano en coordenadas cilíndricas

A veces es ventajoso describir el movimiento de un punto en un plano en términos de la distancia\(r\) desde el origen y el ángulo\(\theta\) medido desde el\(x\) eje positivo, es decir, coordenadas cilíndricas. Utilizando las definiciones de velocidad y aceleración como primera y segunda derivadas de posición con respecto al tiempo y se pueden desarrollar las relaciones trigonométricas entre\(x, y, r,\) y\(\theta\) las siguientes relaciones:

Figura\(\PageIndex{3}\): Tabla de vectores unitarios y relaciones de posición, velocidad y ecuación de aceleración entre coordenadas rectangulares y cilíndricas.

(a) Comenzando con el vector de posición\(\mathbf{r}\), mostrar eso\(\mathbf{e}_{\mathrm{r}}=(\cos \theta) \mathbf{i}+(\sin \theta) \mathbf{j}\).

(b) Ahora diferencie\(\mathbf{e}_{\mathbf{r}}\) con respecto al tiempo y demuéstrate eso a ti mismo\(\dfrac{d}{d t} \mathbf{e}_{\mathbf{r}}=\omega \mathbf{e}_{\theta}\).

c) ¿Cómo se simplifican las relaciones para\(\mathbf{r}, \mathbf{V}\), y\(\mathbf{a}\) en coordenadas cilíndricas si\(r=R\), una constante?

d) ¿Cómo se simplifican las relaciones para\(\mathbf{r}, \mathbf{V}\), y\(\mathbf{a}\) en coordenadas cilíndricas si son\(\omega=\) constantes?

Ejemplo — Momento lineal de un disco circular

Un disco circular de radio\(R\) y grosor\(t\) está hecho de un material con densidad\(\rho\). Determine el momento lineal para el disco bajo las siguientes condiciones:

(a) El disco está rotando con una velocidad de rotación\(\omega\) alrededor de su eje centroidal,\(G\). A pesar de que este disco parece tocar el suelo, se está deslizando y no está rodando.

(b) El disco se desliza hacia la derecha sin girar, es decir\(\omega=0\). El disco se está trasladando con velocidad\(\mathbf{V}\).

Figura\(\PageIndex{4}\): Dada la información sobre el disco.

Solución:

Conocido: Un disco circular se mueve con un movimiento especificado.

Buscar: (a) Momento lineal cuando el disco gira alrededor de su eje centroidal.
(b) Momento lineal cuando el disco se traslada con velocidad\(\mathbf{V}\).

Dado: Ver figura anterior.

Análisis: Estrategia\(\rightarrow\) Utilizar la definición de impulso lineal.

(a) La velocidad del disco giratorio medida con respecto al centro de masa\(G\) es\(\mathbf{V} = r \omega \mathbf{e}_{\theta} = r \omega \left( -(\sin \theta) \mathbf{i}+(\cos \theta) \mathbf{j} \right)\). Usando la definición de impulso lineal de un sistema que tenemos\[\begin{aligned} \mathbf{P}_{\mathrm{sys}} &= \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = \int\limits_{0}^{2 \pi} \int\limits_{0}^{R} \underbrace{ \left(r \omega \mathbf{e}_{\theta} \right) }_{\mathbf{V}} \rho \underbrace{ (r \ d \theta \ dr) }_{d V\kern-0.5em\raise0.3ex-} \\ &= (\rho \omega) \int\limits_{0}^{2 \pi} \underbrace{ ((\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j}) }_{\mathbf{e}_{\theta}} \left( \int\limits_{0}^{R} r^{2} \ dr \right) d \theta = (\rho \omega) \int\limits_{0}^{2 \pi} \underbrace{ ((\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j}) }_{\mathbf{e}_{\theta}} \left( \frac{R^{3}}{3}\right) d \theta \\ &= \left( \frac{\rho \omega R^{3}}{3} \right) \int\limits_{0}^{2 \pi} \left( (\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j} \right) \ d \theta \\ &=\left( \frac{\rho \omega R^{3}}{3} \right) \left[ \mathbf{i} \int\limits_{0}^{2 \pi}(\sin \theta) \ d \theta - \mathbf{j} \int_{0}^{2 \pi}(\cos \theta) \ d \theta \right] = \left( \frac{\rho \omega R^{3}}{3} \right)(0)=0 \end{aligned} \nonumber \]

Así, como habrás adivinado el momento lineal de un disco que gira alrededor de su eje centroidal es idénticamente cero. En general, el momento lineal de un sistema que gira alrededor de un eje fijo es siempre cero si (1) el eje de rotación pasa por el centro de masa, es decir, su eje centroidal, y (2) el sistema tiene un plano de simetría que es perpendicular al eje de rotación. Si se viola alguna de estas dos condiciones, el impulso lineal no será cero.

Tenga en cuenta que esta integración podría haberse simplificado mucho si hubiéramos utilizado la integral para la velocidad del centro de masa, la Ec. \((5.1.16)\). El centro de masa\(G\) del disco está en el eje de rotación y el eje de rotación no se traslada; así,\[\mathbf{P}_{\mathrm{sys}} = \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}}(\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = m_{s y s} \cancel{ V_{G} }^{=0} =0 \nonumber \] y el momento lineal del sistema es cero. ¡Esto es mucho más fácil que hacer la integración completa!

(b) Comenzando con la definición de momento lineal y el hecho de que el disco se está traduciendo con velocidad\(\mathbf{V}\), tenemos\[\begin{aligned} \mathbf{P}_{\mathrm{sys}} &= \int\limits_{V\kern-0.5em\raise0.3ex-_{\text {sys}}}(\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = \int\limits_{0}^{2 \pi} \int\limits_{0}^{R}(\mathbf{V} \rho) \underbrace{ (rt \ d \theta \ d r)}_{d V\kern-0.5em\raise0.3ex-} = (\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \int\limits_{0}^{R} r \ dr \ d \theta \\ &=(\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \left(\int\limits_{0}^{R} r \ dr \right) d \theta = (\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \left(\frac{R^{2}}{2}\right) d \theta \\ &= (\mathbf{V} \rho t) \left( \frac{R^{2}}{2}\right) \int\limits_{0}^{2 \pi} d \theta =(\mathbf{V} \rho t) \left(\frac{R^{2}}{2}\right)(2 \pi) \\ &= \underbrace{ \left( \rho \left(\pi R^{2} t\right)\right) }_{\rho V\kern-0.5em\raise0.3ex- _{\text{sys}}} \mathbf{V} = m_{sys} \mathbf{V} \end{aligned} \nonumber \]

Así, el momento lineal es solo el producto de la velocidad de traslación y la masa del sistema. Nuevamente, este cálculo puede simplificarse enormemente usando la ecuación para la velocidad del centro de masa:\[\mathbf{P}_{\mathrm{sys}}=\int_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = m_{s y s} \cancel{ \mathbf{V}_{G} }^{=\mathrm{V}} = m_{sys} \mathbf{V} \nonumber \]