5.4: Impulso Lineal, Momentum Lineal y Fuerzas Impulsivas

Como ya hemos demostrado, a veces es necesario integrar la forma de tasa de la ecuación de conservación de momento lineal en un intervalo de tiempo específico. Esto da una relación entre el cambio de impulso lineal dentro del sistema y la cantidad de impulso lineal transportado al sistema. Históricamente, este tipo de cálculos se han realizado a través de la introducción de una cantidad conocida como impulso lineal. Bajo ciertas condiciones, un sistema estará sometido a una fuerza relativamente grande en un intervalo de tiempo muy corto, como el contacto entre dos bolas de billar o el impacto entre dos autos a medida que chocan. Estas fuerzas grandes y de corta duración se conocen como fuerzas impulsivas y la interacción se conoce como un impacto. En esta sección demostraremos que los cálculos de impacto para las fuerzas impulsivas e impulsivas se derivan naturalmente de nuestra comprensión de la conservación básica de la ecuación de impulso lineal.

5.4.1 Impulso Lineal

Cuando una fuerza actúa sobre el límite de un sistema, el impulso lineal fluye a través del límite a una velocidad especificada: cuanto mayor sea la magnitud de la fuerza, mayor será la tasa de transporte del impulso lineal. Si consideramos una partícula simple con una sola fuerza que\(\mathbf{F}\) actúa sobre ella, sabemos que la tasa de cambio del momento lineal del sistema es\[\frac{d \mathbf{P}_{\mathrm{sys}}}{d t}=\mathbf{F} \nonumber \]

Por definición, el impulso lineal de la fuerza\(\mathbf{F}\) es la integral de la fuerza con respecto al tiempo:\[\mathbf{Impulse }_{t_{1} \rightarrow t_{2}} = \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt \nonumber \]

Como puede verse en la Figura\(\PageIndex{1}\), ésta representa el área bajo una\(\mathbf{F}\) -\(t\) curva.

Figura\(\PageIndex{1}\):\(\mathbf{F}\) -\(t\) curva.

Para la partícula, vemos que el impulso de fuerza\(\mathbf{F}\) solo equivale al cambio en el momento lineal de la partícula:\[\mathbf{Impulse} \left. \right|_{\mathbf{F}, \ t_{1} \rightarrow t_{2}} = \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt = \int\limits_{t_{1}}^{t_{2}} \left( \frac{d \mathbf{P}_{\mathrm{sys}}}{d t} \right) dt = \mathbf{P}_{\mathrm{sys}, 2}-\mathbf{P}_{\mathrm{sys}, 1} \nonumber \]

Para cualquier sistema, el impulso de una fuerza dada es igual a la cantidad de impulso lineal transferido a través del límite del sistema en el intervalo de tiempo especificado. No siempre equivale al cambio en el impulso lineal del sistema. Frecuentemente, es imposible medir directamente la magnitud de la fuerza en función del tiempo. En este caso, es una práctica común hablar del impulso de la fuerza y, si es posible, determinar el impulso midiendo el cambio en el momento lineal del sistema.

5.4.2 Fuerzas Impulsivas

La incapacidad de medir los detalles de una fuerza dada en función del tiempo es especialmente cierta durante los impactos. Una fuerza impulsiva es una fuerza relativamente grande que actúa a lo largo de un período de tiempo muy corto, por ejemplo, cuando una bola de boliche golpea una bolera. Cuando esto ocurre, la bola de boliche transfiere el impulso lineal al pasador mediante una fuerza de contacto de corta duración. Lo mismo sería cierto del impulso lineal impartido a un lanzamiento de jonrón ya que el beisbol impacta el bate del bateador por un periodo muy corto de tiempo. Por un intervalo de tiempo muy pequeño, es posible estimar la magnitud de la fuerza impulsiva promedio asumiendo que la fuerza es constante en el intervalo de tiempo pequeño:\[\mathbf{F}_{\text {avg }} \Delta t = \int\limits_{t}^{t+\Delta t} \mathbf{F} \ dt = \left. \mathbf{Impulse} \right|_{\mathbf{F}, \ t_{1} \rightarrow t_{2}} \quad \rightarrow \quad \mathbf{F}_{\text {avg}} = \frac{1}{\Delta t} \int\limits_{t}^{t+\Delta t} \mathbf{F} \ dt \nonumber \] Como se muestra en la Figura\(\PageIndex{2}\), la fuerza impulsiva promedio es igual a la fuerza constante que actúa en el mismo intervalo de tiempo y transfiere la misma cantidad de impulso lineal que la fuerza original variable en el tiempo.

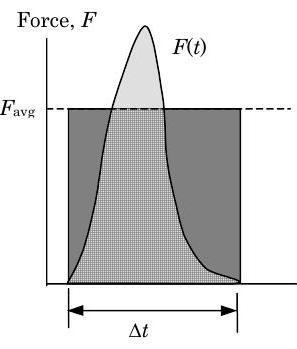
Figura\(\PageIndex{2}\): Fuerza impulsiva.

Pruebe su comprensión: estimación de la fuerza máxima durante la carga por impulso

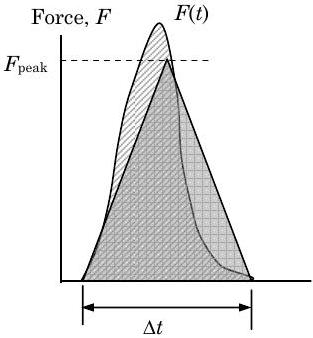
Al calcular la fuerza impulsiva promedio anterior hemos asumido que la forma y el área de la\(t\) curva\(\mathbf{F}\) - se pueden aproximar mejor mediante una caja rectangular de altura\(F_{\text {avg}}\) y anchura\(\Delta t\). Hay otras formas posibles que podríamos usar para aproximar la\(t\) curva\(\mathbf{F}\) -. Supongamos que aproximamos el área bajo la\(t\) curva\(\mathbf{F}\) - usando un triángulo isósceles de altura\(F_{\text {peak}}\) y base\(\Delta t\).

¿Cuál es la relación entre\(F_{\text {avg}}\) y\(F_{\text {peak}}\) para una situación de carga impulsiva de duración\(\Delta t\)? ¿Qué valor da una mejor estimación de la fuerza máxima experimentada por el sistema durante el impacto y por qué es mejor?

Figura\(\PageIndex{3}\): Aproximación de fuerza impulsiva usando triángulo isósceles.

Ejemplo — Boxcars colisionando

Dos vagones se van a acoplar entre sí en un patio de distribución de ferrocarriles. El vagón A se mueve hacia la derecha con una velocidad de\(3 \mathrm{~km} / \mathrm{h}\) y se va a acoplar al vagón B, que inicialmente está estacionario. El vagón A tiene una masa de\(45,000 \mathrm{~kg}\) y el vagón B tiene una masa de\(25,000 \mathrm{~kg}\).

Determinar (a) la velocidad final de los carros acoplados, y (b) la fuerza impulsiva promedio que actúa sobre cada carro durante el acoplamiento si el proceso de acoplamiento toma\(0.3 \ \text{s}\).

Solución

Conocido: Dos vagones chocan y se acoplan entre sí.

Encuentra: (a) velocidad final de los autos acoplados

(b) fuerza impulsiva promedio sobre los automóviles si el proceso de acoplamiento toma\(0.3 \ \text{s}\).

Dado:

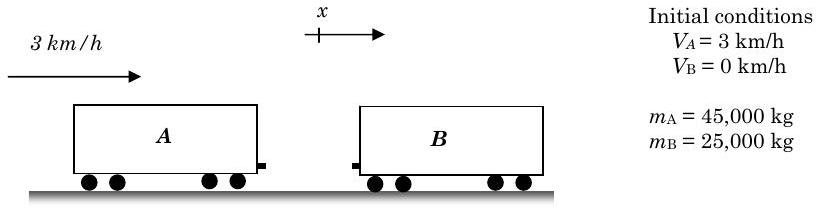
Figura\(\PageIndex{4}\): Condiciones iniciales y posiciones relativas de dos vagones.

Análisis:

Estrategia\(\rightarrow\) Dado que este problema involucra dos objetos colisionando con un impacto, intente observar la conservación del impulso lineal.

Sistema Aún no\(\rightarrow\) estoy seguro, voy a decidir esto en un minuto.

Propiedad para contar Momento\(\rightarrow\) lineal en la\(x\) dirección -.

Intervalo de tiempo Tiempo\(\rightarrow\) finito desde interesado en el comportamiento antes y después.

Ahora considera qué sistema elegir. Intentemos usar un sistema cerrado de mudanzas que incluya solo los vagones.

Figura\(\PageIndex{5}\): Elección del sistema, antes y después de la colisión.

Observe que si solo consideramos\(x\) -momentum, no hay fuerzas que actúen sobre el sistema con un componente en la\(x\) dirección -dirección. Así que la conservación de la ecuación de impulso lineal se convierte\[\frac{d P_{x, \ \text{sys}}}{dt} = \sum \underbrace{F_{x \ \text {external}}}_{\text {No } x \text{-forces}} + \underbrace{ \sum_{i} \cancel{ \dot{m} V_{x, i} }^{=0} - \sum_{e} \cancel{ \dot{m} V_{x, e} }^{=0} }_{\text {Closed System}} \rightarrow P_{x, \ \text{sys}} = \text {constant} \nonumber \]

El uso de este resultado para relacionar el momento lineal del sistema antes y después del impacto da lo siguiente:\[\begin{gathered} &P_{x, \ 1} = m_{A} V_{A, \ 1} + m_{B} \cancel{V_{B, \ 1}}^{=0} \\ &P_{x, 2} = m_{A} \cancel{ V_{A, \ 2} }^{=V_{2}} +m_{B} \cancel{ V_{B, 2} }^{=V_{2}} \end{gathered} \rightarrow \quad \rightarrow \quad \begin{gathered} P_{x, \ 1} = P_{x, \ 2} \\ m_A V_{A, \ 1} = \left( m_{A}+m_{B} \right) V_{2} \end{gathered} \quad \rightarrow \quad V_{2} = \frac{m_{A}}{\left(m_{A} + m_{B}\right)} V_{A, \ 1} \nonumber \]

Resolviendo para la velocidad final que tenemos\(V_{2} = \dfrac{m_{A}}{\left(m_{A}+m_{B}\right)} V_{A, \ 1} = \dfrac{45}{(45+25)}\left(3 \ \dfrac{\mathrm{km}}{\mathrm{h}}\right) = 1.93 \mathrm{~km} / \mathrm{h}\).

Y como se trata de un número positivo, los trenes acoplados continuarán moviéndose hacia la derecha (\(x\)dirección positiva). Esta es la respuesta a la Parte (a).

Ahora para determinar la fuerza impulsiva promedio, debemos colocar un límite donde se produzca la fuerza. Considerar un sistema cerrado que incluya únicamente vagón B. Comenzando con la conservación del impulso lineal para este sistema cerrado da\( \dfrac{d P_{x, \ \text{sys}}}{d t} = F_{\text {coupling}} \).

Figura\(\PageIndex{6}\): Sistema cerrado compuesto por el Boxcar B.

Pero para encontrar la fuerza de acoplamiento promedio en el auto B, debemos integrar esta expresión en el intervalo de tiempo:\[\int\limits_{t_{1}}^{t_{2}} \left( \frac{d P_{x, \ \text{sys}}}{d t} \right) dt = \int\limits_{t_{1}}^{t_{2}} F_{\text {coupling }} dt \quad \rightarrow \quad P_{x, \ 2} - P_{x, \ 1} = F_{\text {coupling, avg }} \Delta t \nonumber \] Resolviendo por la fuerza que tenemos\[\begin{aligned} F_{\text {coupling, avg}} &= \frac{P_{x, \ 2}-P_{x, \ 1}}{\Delta t} = m_{B} \frac{V_{B, \ 2}-V_{B, \ 1}}{\Delta t} \\[4pt] &=(25,000 \mathrm{~kg}) \left[ \frac{(1.93-0) \ \dfrac{\mathrm{m}}{\mathrm{h}}}{(0.3 \mathrm{~s})} \right] \left( \frac{\mathrm{h}}{3600 \mathrm{~s}} \right) \left( \frac{\mathrm{N} \cdot \mathrm{s}^{2}}{\mathrm{kg} \cdot \mathrm{m}} \right) = 44.7 \times 10^{3} \mathrm{~N} = 44.7 \ \mathrm{kN} \end{aligned} \nonumber \]

Dado que el valor es positivo, la dirección de la fuerza de acoplamiento en el carro B es como se muestra en la figura. La fuerza de acoplamiento que actúa sobre el carro A es de la misma magnitud y dirección opuesta.

Comentar

(1) Considerar un sistema alternativo para resolver la Parte (a). Esta vez se asume un sistema abierto que inicialmente incluye el automóvil B y finalmente incluye ambos autos.

Comenzando con la ecuación de impulso lineal:\[ \frac{d P_{x, \ \text{sys}}}{dt} = \underbrace{ \sum \cancel{ F_x }^{=0} }_{\text{No forces in } x \text{-direction} } + \,\,\,\, \dot{m}_i V_{x, \ i} \,\,\,\, - \underbrace{ \cancel{ \dot{m}_e V_e }^{=0} }_{\text{No flow out of system}} \quad\quad \rightarrow \quad\quad \frac{ d P_{x, \ \text{sys}} }{dt} = \underbrace{ \dot{m}_i V_{x, \ i} }_{\begin{array}{c} x \text{-momentum carried} \\ \text{in with boxcar A} \end{array} } \nonumber \]

Para encontrar la velocidad (o momento lineal) del sistema después del acoplamiento debemos integrar esta ecuación a lo largo del intervalo de tiempo:\[ \int\limits_{t_1}^{t_2} \left( \frac{d P_{x, \ \text{sys}}}{dt} \right) dt = \underbrace{ \int\limits_{t_1}^{t_2} \left( \dot{m}_i V_i \right) dt }_{\begin{array}{c} = \text{ all of the momentum} \\ \text{carried into the system} \\ \text{by boxcar A} \end{array}} \quad \rightarrow \quad \underbrace{ P_{x, \ 2} }_{\begin{array}{c} \text{Includes} \\ \text{both cars} \end{array}} - \underbrace{ P_{x, \ 1} }_{\begin{array}{c} \text{Only} \\ \text{car B} \end{array}} = m_A V_A \quad\quad \rightarrow \quad\quad \left( m_A + m_B \right) V_2 = m_A V_A \nonumber \]

La solución continúa a partir de este punto como antes. Observe cómo a partir de un sistema diferente, incluso un sistema abierto, podemos recuperar la misma ecuación usando suposiciones consistentes. Esto ilustra que a menudo es posible resolver el mismo problema usando varios sistemas diferentes.

(2) Seleccione un sistema abierto que tenga masa entrando y saliendo durante el impacto y resuelva la velocidad final de los autos acoplados. [Sugerencia: Este sistema no tendría impulso lineal ni en el estado inicial ni en el final.]

(3) ¿Cuánto tiempo tardarían los autos acoplados en detenerse por completo si los frenos del carro B estuvieran bloqueados en el momento del impacto y el coeficiente de fricción cinética entre las ruedas y el riel es\(0.10\)? ¿Cuál sería la velocidad de los autos acoplados inmediatamente después del impacto? ¿Sería razonable descuidar la fuerza de fricción durante el impacto? [Respuesta:\(1.53\) segundos].