6.4: Problemas
- Page ID
- 86299
El soporte\(BCD\) está abisagrado\(C\) y unido a un cable de control en\(B\). Para la carga mostrada, determinar (a) la tensión en el cable, (b) la reacción a\(C\). [Recuerde seleccionar explícitamente un sistema, aplicar las ecuaciones básicas y establecer sus suposiciones simplificadoras.]
.png)
Figura\(\PageIndex{1}\): Un soporte se carga con dos fuerzas puntuales.
(Adaptado de Beer & Johnston, Dynamics, 6a ed., McGraw-Hill)
El grano cae de una tolva a una tolva\(C B\) a razón de\(240 \ \mathrm{lbm} / \mathrm{s}\). Golpea la tolva a\(A\) una velocidad de\(20 \ \mathrm{ft} / \mathrm{s}\) y sale a\(B\) con una velocidad de\(15 \ \mathrm{ft} / \mathrm{s}\), formando un ángulo de\(10^{\circ}\) con la horizontal. Sabiendo que el peso combinado de la tolva y del grano que soporta es\(600 \ \mathrm{lbf}\) y actúa\(G\), determinar la reacción del soporte del rodillo\(B\) y los componentes de la reacción en la bisagra\(C\).
.jpg)
Figura\(\PageIndex{2}\): Vista lateral del grano que cae sobre un conducto curvo y sale en una corriente en ángulo.
[Asegúrese de esbozar su sistema cuidadosamente para que pueda ver lo que está sucediendo. No asuma que conoce ninguna dimensión que no sean las que se le dan en la declaración del problema y la figura. También tenga en cuenta que puede calcular el momento angular alrededor de cualquier punto dentro o en el límite del sistema. Por lo general, lo mejor es escoger el punto que minimice los cálculos o donde los transportes de momento angular sean más fáciles de ver.]
(Adaptado de Pestel & Thomson, Statics, McGraw-Hill)
Para el dispositivo de sujeción que se muestra en la figura, determinar las fuerzas\(\mathbf{F}_{1}\) y\(\mathbf{F}_{2}\).
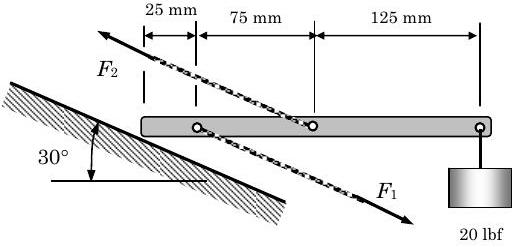
Figura\(\PageIndex{3}\): Un dispositivo de sujeción experimenta dos fuerzas de tensión desconocidas.
(Adaptado de Pestel & Thomson, Statics, McGraw-Hill)
Un carro monorraíl con las dimensiones que se muestran en la figura es conducido solo por la rueda delantera. Si el coeficiente de fricción estática entre la rueda y el riel es\(0.60\), determine la aceleración máxima posible para el automóvil.
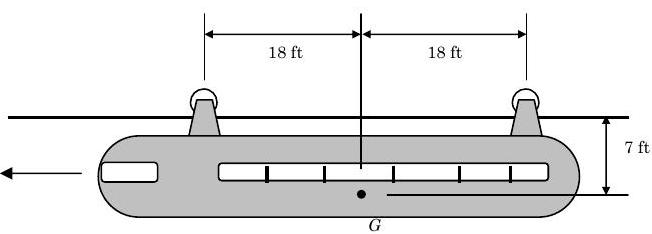.jpg)
Figura\(\PageIndex{4}\): Un monorraíl cuelga debajo de una pista, soportado por sus ruedas.
- Contestar
-
\(0.340 \mathrm{~g}\)
El remolque cargado que se muestra en la figura tiene una masa de\(900 \mathrm{~kg}\) con un centro de masa en\(G\) y está unido\(A\) a un enganche de parachoques trasero. Las dimensiones pertinentes se dan en el diagrama.
(a) Determinar el componente vertical de la fuerza del enganche que actúa sobre el remolque\(A\) cuando el remolque está estacionario. Da tanto la magnitud, en newtons, como la dirección de la fuerza.
(b) Si el carro acelera hacia la derecha a la velocidad de\(4.5 \mathrm{~m} / \mathrm{s}^{2}\), determinar la componente vertical de la fuerza de enganche que actúa sobre el remolque en\(A\). Olvidar la pequeña fuerza de fricción ejercida sobre las ruedas relativamente ligeras. Da tanto la magnitud, en newtons, como la dirección de la fuerza.
.jpg)
Figura\(\PageIndex{5}\): Vista lateral de un tráiler cargado.
Tus amigos te han desafiado a equilibrar un palo de escoba en tu mano. Para que no te avergüences, has decidido hacer algunos análisis antes de montar un programa.
Como primera aproximación, se asume que la escoba sólo puede moverse en el plano del papel. La escoba tiene una masa\(m = 2.0 \mathrm{~lbm}\) y una longitud total\(L = 5 \mathrm{~ft}\). El centro de masa de la escoba, incluidas las cerdas, se encuentra a una\(0.6 L\) distancia del extremo del mango de la escoba
Si comienzas a equilibrar la escoba cuando ésta se inclina un ángulo\(\theta=30^{\circ}\) desde la vertical, tu reto es mover tu mano horizontalmente para que la escoba mantenga esta orientación, es decir, se someta a traslación lineal. Ya que no puedes agarrar la escoba, asume que tu mano sólo puede resistir fuerzas en las direcciones\(x\) - y\(y\) -direcciones.
Para estas condiciones, determina (a) la magnitud y dirección de la reacción de tu mano sobre la escoba, y (b) la dirección y magnitud de la aceleración horizontal de la escoba.
.png)
Figura\(\PageIndex{6}\): Una escoba se equilibra en una mano a través del extremo de su escoba.
Una turbina de rueda Pelton se utiliza para extraer energía de una corriente de agua que fluye. Cuando está operando en condiciones de estado estacionario, la corriente de agua ingresa a la rueda de turbina giratoria como se muestra con velocidad\(V_{1}\) y sale de la turbina con velocidad\(V_{2}\) en ángulo\(\theta\). Bajo estas condiciones, la rueda de turbina gira alrededor del eje a través del punto\(O\). El punto negro en\(O\) representa el eje de la turbina. Para la operación en estado estacionario, se\(M_O\) deben aplicar dos fuerzas de reacción\(R_{\mathrm{x}}\)\(R_{\mathrm{y}}\) y un par (o momento) al eje en el punto\(O\).
Si el caudal másico es\(50 \mathrm{~kg} / \mathrm{s}\) y\(V_{1}=V_{2}=30 \mathrm{~m} / \mathrm{s}\), determine las dos fuerzas de reacción y el par a\(O\) if\(\theta=\) (a)\(0^{\circ}\), (b)\(30^{\circ}\), (c)\(60^{\circ}\), (d)\(90^{\circ}\), (d)\(120^{\circ}\), (e)\(150^{\circ}\) y (f)\(180^{\circ}\).
.jpg)
Figura\(\PageIndex{8}\): El agua corre a lo largo de una sección de una turbina de rueda, girándola en sentido horario.
(Adaptado de Bedford & Wallace, Dynamics, 2a ed., Addison-Wesley)
La barra esbelta pesa\(10 \ \mathrm{lbf}\) y el disco pesa\(20 \ \mathrm{lbf}\). El coeficiente de fricción cinética entre el disco y la superficie horizontal es\(0.1\). Si el disco tiene una velocidad angular inicial en sentido antihorario de\(10 \ \mathrm{rad} / \mathrm{s}\), cuánto tiempo tarda el disco en dejar de girar.
.jpg)
Figura\(\PageIndex{9}\): Una barra en ángulo tiene un extremo anclado a una pared y el otro anclado a un disco que descansa sobre el suelo.
El agua fluye fuera de una boca de incendios con una velocidad de\(50 \ \mathrm{ft} / \mathrm{s}\) y un caudal volumétrico de\(1000 \ \mathrm{gpm}\). La presión del agua en la entrada a la boca de riego es\(200 \ \mathrm{psia}\) y la presión atmosférica es\(14.7 \ \mathrm{psia}\). En la base de la boca de riego, los pernos deben resistir una fuerza normal que sostiene la boca de riego hacia abajo, una fuerza de cizallamiento paralela al suelo y una pareja tratando de rotar la boca de riego fuera de su base. Calcular estas reacciones asumiendo condiciones de estado estacionario. Supongamos que la densidad del agua es\(62.4 \ \mathrm{lbm} / \mathrm{ft} ^{3}\).
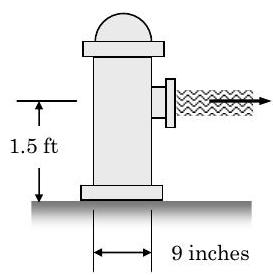
Figura\(\PageIndex{9}\): Vista lateral de una boca de incendios con agua que sale de su boquilla en una corriente horizontal.
El marco mostrado soporta parte de un pequeño edificio. Sabiendo que la tensión en el cable es\(150 \ \mathrm{kN}\), determinar la reacción en el extremo fijo\(E\) (fuerzas y momento).
.jpg)
Figura\(\PageIndex{10}\): Un marco que consta de dos vigas y dos cables de soporte se carga con varias cargas puntuales.
Un chorro de aire de alta velocidad sale de la boquilla\(A\), que tiene un diámetro de\(40 \mathrm{~mm}\), con una velocidad\(240 \mathrm{~m} / \mathrm{s}\) y un caudal másico de\(0.36 \mathrm{~kg} / \mathrm{s}\) e incide sobre la paleta\(OB\), que se muestra en su vista de borde. La paleta y su extensión en ángulo recto tienen una masa insignificante en comparación con el\(6 \mathrm{-kg}\) cilindro adjunto, y se pivotan libremente alrededor de un eje horizontal a través de\(O\). La densidad del aire bajo la condición imperante es\(1.206 \mathrm{~kg} / \mathrm{m}^3\).
Determinar:
(a) el ángulo de estado estacionario\(\theta\) asumido por la paleta con la horizontal, y
(b) las fuerzas de reacción en\(O\).
.jpg)
Figura\(\PageIndex{11}\): Un chorro de aire viaja horizontalmente hasta que impacta sobre una superficie inclinada, moviéndose a velocidad constante en todo momento.
Una bola con masa\(m=5 \ \mathrm{lbm}\) se monta sobre una varilla horizontal que es libre de girar alrededor de un eje vertical como se muestra en la figura. En la posición mostrada (posición\(A\)), la varilla gira y la bola es sujetada por un cordón unido al eje. En este estado, la velocidad de la pelota es\(V_1=24 \ \mathrm{in} / \mathrm{s}\). El cordón se corta repentinamente y la bola se mueve a la posición a\(B\) medida que la varilla continúa girando. Descuidando la masa de la varilla, determinar la velocidad de la pelota después de que haya llegado al tope\(B\). Ten cuidado de mostrar todo tu trabajo.
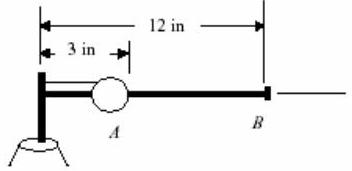
Figura\(\PageIndex{12}\): Dos posiciones instantáneas de una bola en relación con una varilla giratoria en un eje.
(De Dynamics by Beer and Johnson)
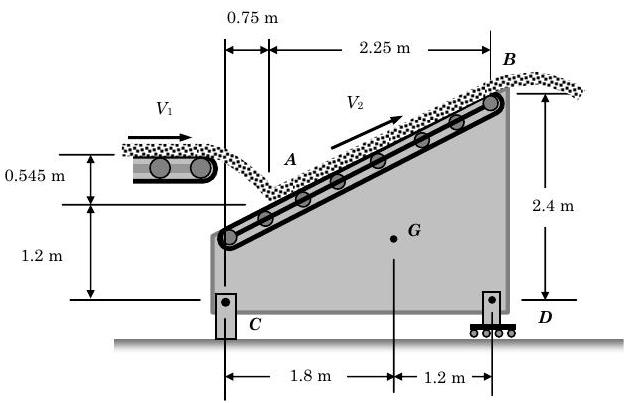
El carbón se está descargando de una cinta transportadora horizontal a razón de\(120 \mathrm{~kg} / \mathrm{s}\). Se recibe en\(A\) por una segunda cinta que la descarga de nuevo en\(B\). Sabiendo eso\(v_{1}= 3 \mathrm{~m} / \mathrm{s}\) y\(\mathrm{v}_{2}=4.25 \mathrm{~m} / \mathrm{s}\), y que el segundo conjunto de cinta y el carbón que soporta tienen una masa total de\(472 \mathrm{~kg}\), determinar componentes horizontales y verticales de las reacciones en\(C\) y\(D\).
.jpg)
Figura\(\PageIndex{13}\): El carbón cae de una cinta transportadora horizontal sobre una diagonal donde se descarga nuevamente.
Un sistema transportador está equipado con paneles verticales, y una\(300 \mathrm{~mm}\) varilla\(AB\) de masa\(2.5 \mathrm{~kg}\) se aloja entre el panel como se muestra. Supongamos que todas las superficies son lisas. Conociendo la aceleración del panel y la varilla está\(1.5 \mathrm{~m} / \mathrm{s}^{2}\) a la izquierda, determinar las reacciones del portador en la varilla en\(C\) y\(B\).
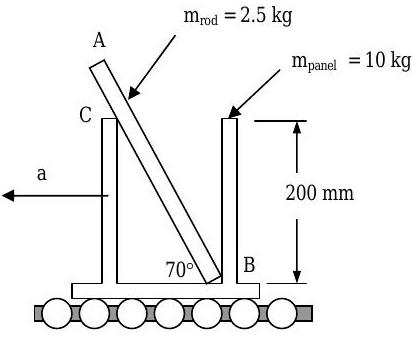
Figura\(\PageIndex{14}\): Una varilla descansa contra dos paneles verticales que viajan a lo largo de una cinta transportadora.
(Modificado de Dynamics por Beer and Johnson)
El montacargas que se muestra pesa\(2250 \ \mathrm{lbf}\) y se utiliza para levantar una caja de peso\(\mathrm{W}=2500 \ \mathrm{lbf}\). El coeficiente de fricción estática entre la caja y la carretilla elevadora es\(0.3\).
Determinar:
(a) la desaceleración máxima que puede tener la carretilla elevadora para que la caja no se deslice, y
(b) la desaceleración máxima que puede tener la carretilla elevadora para que la carretilla elevadora no se incline.
(c) Si el camión se mueve hacia la izquierda a una velocidad de\(10 \ \mathrm{ft} / \mathrm{s}\) cuando se aplican los frenos, determinar la distancia más pequeña en la que el camión puede detenerse si la caja no va a deslizarse y si el camión no va a inclinarse hacia adelante.
.jpg)
Figura\(\PageIndex{15}\): Vista lateral de una carretilla elevadora de dos ejes que levanta una caja.
Parte (a) Se aplican tres fuerzas a la placa en forma de L que se muestra en la figura. Todas las fuerzas se aplican en el plano del papel.
(i) Determinar el momento de cada fuerza sobre Punto\(O\) y la suma de los momentos sobre Punto\(O\), en\(\text{lbf-ft}\).
(ii) Determinar el momento de cada fuerza sobre Punto\(P\) y la suma de los momentos sobre Punto\(P\), en\(\text{lbf-ft}\).
(iii) ¿Alguna de las fuerzas aplicadas a la placa forma pareja? Si la respuesta es sí, ¿cuáles?
[Nota: Recuerde indicar tanto la dirección (etiqueta CW o CCW, o usar flechas) como la magnitud de todas las cantidades vectoriales.]
.png)
Figura\(\PageIndex{16 \text{a}}\): Las fuerzas puntuales se aplican en diferentes ubicaciones sobre una placa en forma de L.
Parte (b) Dos fuerzas actúan sobre el cuerpo plano y rígido que se muestra en la figura.
Determinar el momento individual de cada fuerza sobre el punto\(O\) y la suma de los momentos sobre el punto\(O\) en\(\mathrm{N}-\mathrm{m}\). Recuerde indicar la dirección y magnitud de todas las cantidades vectoriales.
Figura\(\PageIndex{16 \text{b}}\): Las fuerzas puntuales se aplican en diferentes ubicaciones sobre una placa de forma irregular.
Considera el sistema polea-masa que se muestra en la figura. Los diámetros de la polea grande y pequeña son\(D = 0.5 \mathrm{~m}\) y\(d = 0.25 \mathrm{~m}\), respectivamente. Ambas poleas giran juntas alrededor del mismo eje, punto\(P\).
(a) Si las poleas están bloqueadas por un freno y no pueden girar, el peso de cada bloque produce un momento alrededor del punto\(P\). Determinar el momento neto sobre el punto\(P\) debido a los bloques estacionarios, en\(\text{N-m}\).
(b) Si las poleas giran juntas a la velocidad de\(2.0\) radianes por segundo en la dirección mostrada, es decir,\(\omega=2.0 \mathrm{rad} / \mathrm{s}\) en la dirección mostrada, cada uno de los bloques tiene momento angular e impulso lineal. Determine lo siguiente para cada bloque:
- la velocidad, en\(\mathrm{m} / \mathrm{s}\),
- el momento lineal, en\(\mathrm{kg-m} / \mathrm{s}\), y
- el momento angular de cada masa con respecto al punto del eje\(\mathrm{P}\), pulg\(\mathrm{kg-m}^{2} / \mathrm{s}\).
Recuerde indicar tanto la magnitud como la dirección de todas las cantidades vectoriales.
.jpg)
Figura\(\PageIndex{17}\): Dos pesos están suspendidos de dos poleas a través de las cuales pasa un solo eje.
Una fuerza horizontal\(\mathbf{P}\) actúa sobre un gabinete que descansa sobre un piso como se muestra. El gabinete pesa\(120 \ \mathrm{lbf}\). Se sabe que el coeficiente de fricción estática es\(\mu_{\mathrm{s}}=0.30\) y el coeficiente de fricción cinética es\(\mu_{\mathrm{k}}=0.24\).
a) Si el deslizamiento se empende, ¿cuál es la magnitud de\(\mathbf{P}\)?
b) Si el vuelco se empende,
(i) cuál es la magnitud de\(\mathbf{P}\), y
ii) ¿en qué momento actuará la reacción de piso resultante?
c) ¿Cuál es la magnitud más pequeña que provocará\(\mathbf{P}\) que el gabinete se mueva, es decir, ya sea de punta o deslizamiento?
.jpg)
Figura\(\PageIndex{18}\): Se aplica una fuerza horizontal a un gabinete alto que descansa sobre el piso.
El agua fluye constantemente a través del conjunto codo-boquilla que se muestra en la figura. El ensamblaje se encuentra en el plano vertical (el plano del papel) y la gravedad actúa como se indica. El conjunto está soportado completamente por los pernos de brida que deben resistir las fuerzas en las\(y\) direcciones\(x\) -y -así como un momento. Para fines de análisis, puede suponer que todas las reacciones de brida se concentran en el “punto” oscuro en la línea central de la brida. La información disponible sobre la geometría y las condiciones de funcionamiento del conjunto se muestran en la figura.
Determine las fuerzas y el momento (las reacciones) en la brida para soportar el conjunto codo-boquilla.
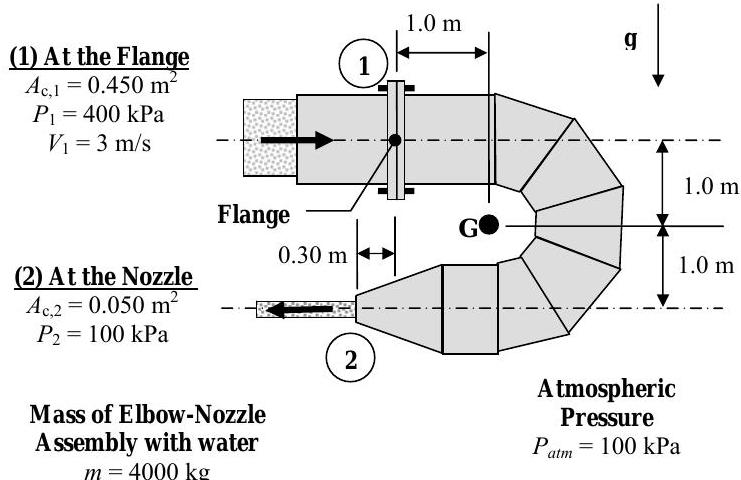
Figura\(\PageIndex{19}\): El agua fluye desde una tubería horizontal hacia un conjunto codo-boquilla, conectada a la tubería por una brida.
Un ciclista viaja en una carretera nivelada a una velocidad\(V=15 \mathrm{~m} / \mathrm{s}\). La masa combinada de la persona y la bicicleta que se muestra en la figura es\(m=77 \mathrm{~kg}\). También se muestra la ubicación del centro de masa combinado con relación a las ruedas.
De pronto el ciclista usa los frenos del manillar para detener la bicicleta. Si solo aplica los frenos delanteros, determine
(a) la fuerza horizontal máxima del suelo (la fuerza de frenado) sobre la bicicleta en el punto\(A\) que se puede aplicar sin que la bicicleta se mueva (descuidar cualquier fuerza horizontal ejercida por el suelo sobre la rueda trasera), y
(b) la desaceleración correspondiente del ciclista y la bicicleta medida en\(g\)'s, por ejemplo\(8.3g\), y
(c) el valor máximo permitido del coeficiente de fricción cinética entre la rueda delantera y el suelo si la rueda delantera se bloquea en estas condiciones y se desliza sobre el suelo.
.jpg)
Figura\(\PageIndex{20}\): Sistema compuesto por un ciclista y una bicicleta, viajando a velocidad constante.
Como parte de un programa de pruebas de seguridad de autobuses escolares, los autobuses escolares están siendo probados para detectar posibles peligros de vuelco. Para probar el autobús, se coloca sobre una almohadilla de concreto\(1000\text{-pound}\) móvil que rueda libremente sin fricción. El movimiento horizontal de la almohadilla es producido por un ariete hidráulico que tira de la almohadilla hacia la izquierda. Se coloca un autobús\(5000 \text{-pound}\) escolar en la plataforma como se muestra en la figura
(a) Suponiendo que el autobús no se deslice sobre la almohadilla, determinar el valor mínimo de la aceleración horizontal\((d V / d t)\) de la almohadilla en la dirección indicada que hará que el autobús se incline, en\(\mathrm{ft} / \mathrm{s}^{2}\).
(b) Determinar la fuerza, en\(\mathrm{lbf}\), que el ariete debe aplicar a la plataforma para producir la aceleración encontrada en la parte (a).
(c) Determinar el coeficiente estático mínimo de fricción entre las llantas y la plataforma de concreto que se requiere para evitar que el autobús se deslice sobre la plataforma móvil.
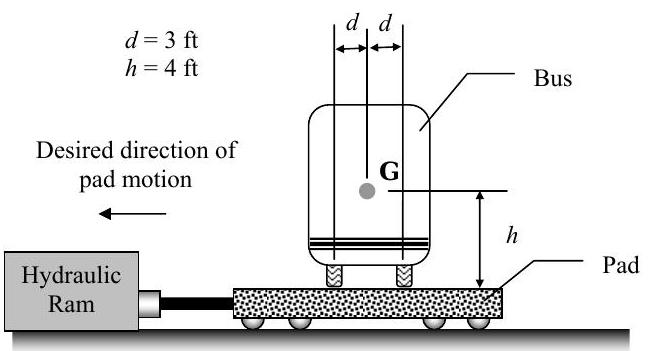
Figura\(\PageIndex{21}\): Vista final de un autobús escolar, colocado sobre una almohadilla rodante que se tira hacia la izquierda.
Un fabricante de cabezales de ducha de mano utiliza la configuración que se muestra en la figura para probar las características de “manejo” de sus cabezales de ducha. Para las pruebas, el cabezal de ducha se cuelga de una tubería vertical de suministro de agua mediante una conexión de unión fija que solo puede resistir fuerzas horizontales y verticales.
El agua ingresa al cabezal de la ducha\(B\) con una velocidad puramente vertical de\(1.00 \ \mathrm{ft} / \mathrm{s}\) y un caudal volumétrico de\(0.0050 \ \mathrm{ft}^{3} / \mathrm{s}\). La presión del agua en la línea de suministro de agua es\(35 \ \mathrm{psia}\).
En la salida de pulverización, la velocidad del agua es\(25 \ \mathrm{ft} / \mathrm{s}\) y la presión es atmosférica (\(P_{\mathrm{atm}}=14.7 \ \mathrm{psia}\)).
El cabezal de ducha de prueba pesa\(1.3 \ \mathrm{lbf}\). Se puede suponer que la densidad del agua es\(62.4 \ \mathrm{lbm} / \mathrm{ft}^{3}\)
Para estas condiciones de prueba de estado estacionario, determinar
(a) el ángulo que hace\(\theta\) el cabezal de ducha con la vertical, y
b) la fuerza de reacción horizontal en la articulación clavada.
.jpg)
Figura\(\PageIndex{22}\): El agua se mueve a través de un sistema que consiste en un cabezal de ducha anclado a una tubería vertical.
Una tubería de acero\(B C\), de longitud\(L_{p}\) con una masa\(m_{p}\), se une al parachoques trasero de una camioneta usando una cuerda ligera\(A B\) de longitud\(L_{r}\). El coeficiente de fricción cinética en el punto\(C\) es\(\mu_{\mathrm{k}}\). Los ángulos que hacen la cuerda y la tubería de acero con la horizontal son constantes y se muestran en la figura.
Determinar la aceleración constante del camión\(a_{\text {truck}}\) y la tensión en la cuerda\(T\) requerida para mantener estas condiciones.
CONFIGURAR PERO NO RESOLVER. Identifique claramente sus incógnitas y el conjunto de ecuaciones que usaría para resolver las incógnitas.
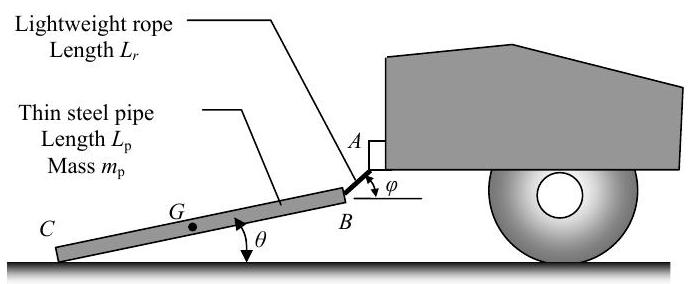
Figura\(\PageIndex{23}\): Una tubería con un extremo apoyada en el suelo está conectada al parachoques de un camión mediante una cuerda tensa.
La unidad de manejo de aire (AHU) mostrada en la figura está unida a un soporte fijo que finalmente descansa sobre el techo. El soporte fijo corresponde con el centro de masa\(G\) de la AHU. El AHU pesa\(500 \ \mathrm{lbf}\).
En la figura se muestran las condiciones de operación esperadas en estado estacionario. Tenga en cuenta que la presión alrededor de la AHU está en todas partes atmosféricas\(P_{\text {atm}}=14.7 \ \mathrm{psia}\), excepto en la entrada de aire (estado 1) donde\(P_{1}=14.6 \ \mathrm{psia}\). Se puede suponer que la densidad del aire es constante y uniforme en\(\rho_{\text {air}}=0.075 \ \mathrm{lbm} / \mathrm{ft}^{3}\).
Determinar las reacciones en el punto\(G\) requerido para apoyar a la AHU.
.jpg)
Figura\(\PageIndex{24}\): Una unidad de manejo de aire con una entrada y una salida se suspende a través de un soporte fijo a través de su centro de masa.
El dragster tiene una masa de\(1200 \mathrm{~kg}\) y un centro de masa en\(G\). Un paracaídas de frenado se fija en\(C\) y, cuando se libera, proporciona una fuerza de frenado horizontal de\(F=k_{\mathrm{O}} V^{2}\) dónde\(k_{\mathrm{O}}=1.6 \mathrm{~N} \cdot \mathrm{s}^{2} / \mathrm{m}^{2}\) y\(V\) es la velocidad del dragster. Si el paracaídas se despliega cuando el dragster viaja demasiado rápido, existe el peligro de que el dragster voltee.
Se puede descuidar la masa de las ruedas y asumir que el motor está desenganchado para que las ruedas estén rodando libremente (así que no hay fuerza horizontal entre las ruedas y el suelo) cuando se suelta el paracaídas.
a) Determinar la velocidad crítica (la velocidad máxima segura) que el dragster puede tener de tal manera que las ruedas a\(B\) estén a punto de abandonar el suelo cuando se libera el paracaídas
b) Si el dragster viaja a la velocidad crítica cuando se despliega el paracaídas, determine la distancia que recorrerá antes de que se detenga. ¿Tiene sentido tu respuesta? Si no, ¿cuál crees que es el problema?
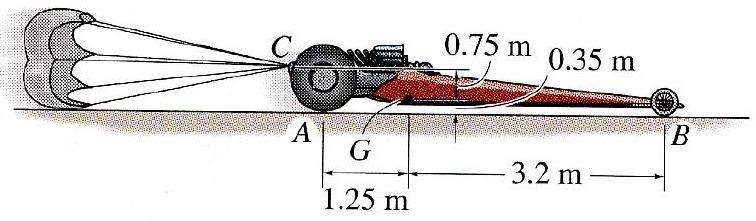
Figura\(\PageIndex{25}\): Un dragster que viaja a la derecha despliega un paracaídas desde su parte trasera.
La viga que se muestra en la figura pesa\(4000 \mathrm{~N}\) y el motor pesa\(1200 \mathrm{~N}\). El motor está levantando una carga que pesa\(8000 \mathrm{~N}\). (Supongamos que el momento de inercia de masa del motor\(I_{\text {motor}}\) es despreciable.)
Determinar las reacciones en\(A\) y\(B\) si el motor está elevando la carga y la carga tiene una aceleración de\(1.5 \mathrm{~m} / \mathrm{s}\) hacia arriba.
.jpg)
Figura\(\PageIndex{26}\): Un motor que descansa sobre una viga gira para elevar una carga.
Un chorro de agua con densidad\(\rho\) golpea un colgajo abisagrado con una masa\(m\) como se muestra en la figura. La velocidad del agua tanto del chorro entrante como de salida es\(V_{\text {jet}}\). El chorro de agua entrante es circular con un diámetro\(d\). Las dimensiones conocidas se dan en la figura.
a) Encontrar el ángulo\(\theta\) que hace el flap estacionario con la horizontal. Exprese su respuesta en términos de las cantidades conocidas.
b) Encontrar las fuerzas de reacción horizontal y vertical en la conexión pin\(A\). Se puede suponer que\(\theta\) se conoce de la parte (a).
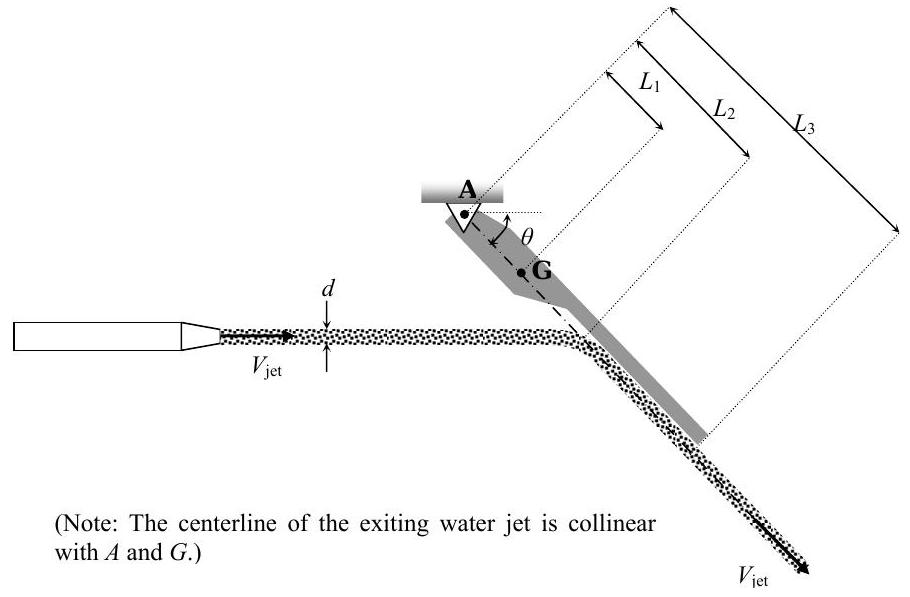
Figura\(\PageIndex{27}\): El agua golpea un colgajo abisagrado en ángulo y corre hacia abajo.
Moo's Dairy ha ingresado a la Dairy Drag Race anual en la Feria Estatal. Su drag racer es un camión de leche completamente cargado que se muestra en la figura. Cuando está completamente cargado, el camión de leche pesa\(5000 \ \mathrm{lbf}\). El camión es un vehículo con tracción trasera, y las llantas delanteras proporcionan un arrastre por fricción insignificante al rodar.
La máxima tracción entre las llantas y la carretera se produce cuando no hay deslizamiento entre las llantas y la carretera, es decir, la fuerza entre la carretera y las llantas se debe a la fricción estática. El coeficiente estático de fricción entre las llantas de goma y el pavimento de concreto es\(\mu_{\mathrm{s}}=0.80\).
a) Determinar las reacciones entre las llantas y la carretera en puntos\(A\) y\(B\), en\(\mathrm{lbf}\), cuando el camión está parado.
(b) Determinar la aceleración máxima posible para el camión lechero totalmente cargado, con tracción trasera, en\(\mathrm{ft} / \mathrm{s}^{2}\) o en\(g\)'s También determinar las reacciones correspondientes en los puntos\(A\) y\(B\), en\(\mathrm{lbf}\). ¿Existe algún peligro de que la camioneta se vuelque en estas condiciones?
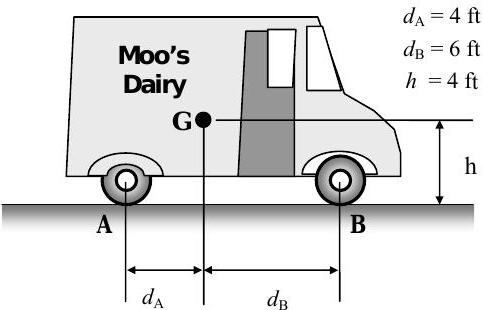
Figura\(\PageIndex{28}\): Vista lateral de un camión lechero en terreno llano.


