6.3: Conservación de la Ecuación de Momentum

El punto de partida recomendado para la aplicación del principio de conservación del momento angular es la forma de tasa de la ecuación:\[\frac{d \mathbf{L}_{O, \text { sys }}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left(\mathbf{r}_{i} \times \mathbf{V}_{i}\right) \dot{m}_{i} - \sum_{out} \left(\mathbf{r}_{e} \times \mathbf{V}_{e}\right) \dot{m}_{e} \nonumber \] donde\(\mathbf{L}_{O, \text { sys}}\) está el momento angular del sistema alrededor del punto\(O\),\(\mathbf{M}_{O}\) es la tasa de transporte del momento angular alrededor del punto\(O\) con momentos, y\(\dot{m}(\mathbf{r} \times \mathbf{V})\) es la velocidad de transporte del momento angular alrededor del punto\(O\) con flujo másico a través del límite.

Al aplicar la forma de tasa de la ecuación de conservación de momento angular, hay muchos supuestos de modelado que se utilizarán para simplificar la ecuación básica para sistemas específicos. Como siempre, debes enfocarte en entender el significado físico de las suposiciones y cómo simplifican las ecuaciones para un sistema dado. No se limite a memorizar los resultados.

Sistema de estado estacionario: Si un sistema está operando en condiciones de estado estacionario, todas las propiedades e interacciones intensivas son independientes del tiempo. Cuando esta suposición se aplica a la conservación de la ecuación de momento angular, tenemos

\[ \begin{align*} \underbrace{ \cancel{ \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} }^{=0} }_{\begin{array}{c} \mathbf{L}_{O, \text{ sys}} \text{ is} \\ \text{constant} \end{array} } &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \dot{m}_i - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \dot{m}_e \\ 0 &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \dot{m}_i - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \dot{m}_e \end{align*} \nonumber \]

Sistema cerrado: Un sistema cerrado no tiene flujo en el límite por lo que la conservación de la ecuación de momento angular se reduce a lo siguiente:\[ \begin{align*} \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \cancel{ \dot{m}_i }^{=0} - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \cancel{ \dot{m}_e }^{=0} \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} &= \sum_{j} \mathbf{M}_{O, \ j} \end{align*} \nonumber \]

Para realizar más simplicaciones, es necesario contar con información adicional o hacer suposiciones sobre la cinemática del sistema de movimiento. Si podemos suponer que un sistema plano se está traduciendo entonces\[\left. \begin{array}{c} \mathbf{L}_{O, \text{ sys}} = m_{\text{sys}} \left( \mathbf{r}_{G} \times \mathbf{V}_{G}\right) \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \end{array} \right\} \quad \rightarrow \quad m_{\text{sys}} \frac{d \left(\mathbf{r}_{G} \times \mathbf{V}_{G} \right)}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \nonumber \]

Si podemos suponer que un plano, sistema rígido está girando alrededor de un eje (el\(z\) -eje) que pasa a través del centro de masa del sistema entonces\[\left. \begin{array}{c} \mathbf{L}_{O, \text{ sys}} = \omega_{z} I_{G} \mathbf{k} \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \end{array}\right\} \quad \rightarrow \quad \frac{d\left(\omega_{z} I_{G} \mathbf{k}\right)}{d t}=\sum_{j} \mathbf{M}_{O, \ j} \nonumber \] donde\(\mathbf{k}\) está el vector unitario los puntos en la dirección positiva del\(z\) eje -eje.

Modelado de reacciones en soportes y conexiones:

Uno de los problemas importantes en la selección de un sistema para la transferencia de impulso es la identificación de las interacciones entre el sistema y su entorno. ¿Cuáles son exactamente las limitaciones sobre cómo se transmite el impulso a través de la frontera en una interacción específica? Las fuerzas de contacto en el límite de un sistema a veces se denominan reacciones, especialmente en lugares donde el límite corta un soporte o conexión. Según Beer y Johnston\(^{1}\), las reacciones pueden clasificarse en tres amplias categorías:

a) Fuerza con una línea de acción conocida. Muchas conexiones satisfacen esta condición entre estas son rodillos, balancines, superficies sin fricción, enlaces y cables cortos, collares en varillas sin fricción y pasadores sin fricción en ranuras. Cada una de estas reacciones se caracteriza por la capacidad de transportar únicamente el momento lineal por una fuerza en una sola dirección claramente identificable. (Ver Figura\(\PageIndex{1}\)).

b) Fuerza de dirección y magnitud desconocidas. El hardware o las conexiones que proporcionan este tipo de reacción incluyen pasadores sin fricción en orificios ajustados, juntas de rótula sin fricción, bisagras y superficies rugosas (Aunque las superficies sin fricción solo transmiten una fuerza normal a la superficie, la fricción introduce fuerzas de cizallamiento en la superficie).

c) Fuerza de dirección y magnitud desconocidas y una pareja. Este último tipo de reacción se suele denominar soporte fijo. La reacción del suelo sobre un poste telefónico pegado verticalmente en el suelo es un excelente ejemplo. Cuando empuja el poste telefónico en cualquier dirección, el suelo ejerce tres fuerzas sobre el poste: una fuerza de corte horizontal, una fuerza normal vertical y una fuerza distribuida que es un par de fuerzas. El par, como se mostró anteriormente, sólo transmite momento angular.

Figura\(\PageIndex{1}\): Reacciones de fuerza superficial.

Como cabría esperar, estas reacciones se pueden ver en la vida cotidiana si uno es observador. Mire a su alrededor ahora mismo y vea si puede encontrar una conexión física que caiga en cada una de estas categorías. Por ejemplo, mire la rueda o rueda de su silla de escritorio o la bisagra de la puerta. La próxima vez que conduzca bajo un paso elevado en la autopista, observe cómo se apoya el lecho de la calzada del puente sobre las columnas. Es muy probable que veas un rodillo.

\(^{1}\)F. P. Beer y E. R. Johnston, Jr., Mecánica vectorial para ingenieros: estática, 6a ed., McGraw-Hill, Nueva York, 1996.

Ejemplo — ¡Qué reacción!

Determinar las reacciones en\(A\) y\(C\). Supongamos que el peso del mecanismo es despreciable y que todas las juntas son sin fricción.

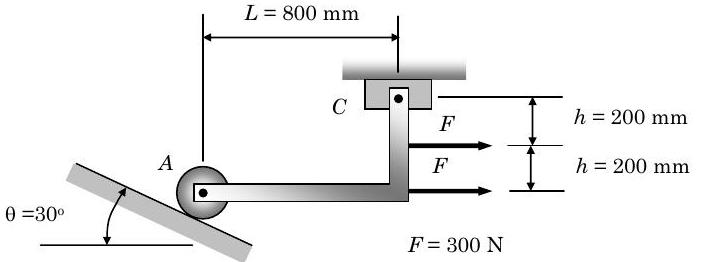
Figura\(\PageIndex{2}\): Una barra en forma de L se soporta en dos extremos y tiene cargas puntuales aplicadas en dos puntos.

Solución

Conocido: Un dispositivo específico con cargas dadas.

Encontrar: Las reacciones (magnitud y dirección) en puntos\(A\) y\(C\).

Dado: Ver figura dibujada anteriormente. (Observe cómo se han dado símbolos a todas las cantidades físicas).

Análisis:

Estrategia\(\rightarrow\) Dado que este problema concierne a las fuerzas, como mínimo requerirá impulso lineal y posiblemente momento angular. (La última parte es un sorteo ya que este problema está en el capítulo del momento angular. Desafortunadamente, los problemas en la vida real nunca vienen con el número de capítulo.)

Sistema\(\rightarrow\) Cerrado, sistema no deformante que incluye la junta con pasadores\(C\), el rodillo en\(A\) y la barra de conexión.
Propiedad para contar Momento\(\rightarrow\) lineal y angular Intervalo de
tiempo\(\rightarrow\) Intentar tasa de forma. (El impulso fluye a través de este sistema).

El sistema dibujado a continuación muestra las reacciones en\(A\)\(C\) y todas las dimensiones pertinentes de la figura. Suponiendo que se trata de un sistema cerrado y de estado estacionario, las ecuaciones de momento lineal y angular se convierten en las siguientes:\[0=\sum_{j} \mathbf{F}_{j} \quad \text { and } \quad 0=\sum_{j} \mathbf{M}_{0, \ j} \nonumber \] (¿Podría mostrar explícitamente cómo se obtuvieron estas dos ecuaciones dadas las suposiciones anteriores?)

Figura\(\PageIndex{3}\): Diagrama de cuerpo libre.

Antes de escribir las ecuaciones de componentes en forma escalar debemos indicar claramente un sistema de coordenadas y lo que estamos asumiendo como direcciones positivas. Esto se hace con el pequeño sistema de coordenadas en la figura. Tenga en cuenta que estamos asumiendo en sentido antihorario (CCW) como la dirección positiva para el momento angular.

Ahora mirando el\(x\) -momentum:

\[ \boxed{ \rightarrow + } \quad\quad 0 = R_{A}(\sin \theta) + 2 F + R_{C x} \quad \rightarrow \quad -2 F = R_{A}(\sin \theta)+R_{C x} \quad \rightarrow \quad -(600 \mathrm{~N}) = R_{A}\left(\sin 30^{\circ}\right)+R_{C x} \nonumber \]

Para el\(y\) -momentum:

\[ \boxed{ \uparrow +} \quad\quad 0 = R_A (\cos \theta) + R_{C y} \quad \rightarrow \quad R_{C y} = - R_A \left( \cos 30 ^{\circ} \right) \nonumber \]

Esto da dos ecuaciones para tres incógnitas —\(R_{A}\),\(R_{C x}\), y\(R_{C y}\). Para obtener la ecuación restante debemos aplicar la conservación del momento angular.

Aplicando la conservación del momento angular sobre el Punto\(A\) eliminamos cualquier momento debido a una de las fuerzas aplicadas\(F\) y la reacción\(R_{A}\):\[ \boxed{ \text {CCW }+ } \quad\quad 0=\left[ +L R_{C y} \right] + \left[-2 h R_{C x}\right] + [-h F] \quad \rightarrow \quad F=\left(\frac{L}{h}\right) R_{C y}-2 R_{C x} \quad \rightarrow \quad (300 \mathrm{~N}) = (4) R_{C y} - 2 R_{C x} \nonumber \]

Resolviendo estas tres ecuaciones simultáneamente, obtenemos lo siguiente:\[\left. \begin{array}{rlrl} -(600 \mathrm{~N}) & =R_{A} \sin 30^{\circ}-2 R_{C x} \\ R_{C y} &= -R_{A} \cos 30^{\circ} \\ (300 \mathrm{~N}) &= R_{A} \sin 30^{\circ}+R_{C x} \end{array} \right\} \quad \rightarrow \quad \begin{aligned} R_{A} &= 365.2 \mathrm{~N} \\ R_{C x} &= -782.6 \mathrm{~N} \\ R_{C y} &= -316.3 \mathrm{~N} \end{aligned} \nonumber \]

Observe que la reacción en\(C\) ocurre en una dirección opuesta a la asumida en el dibujo.

Ejemplo — Ir a la pared para una reacción

Un chorro de agua impacta constantemente una pala que está unida a una viga en voladizo como se muestra en la figura. La viga en voladizo se fija a la pared\(A\) y mantiene la cuchilla estacionaria. El agua golpea la cuchilla\(B\) y la deja en\(C\).

La masa de la combinación hoja/viga es\(100 \ \text{lbm}\) con un centro de masa conocido en un punto\(G\) ubicado a una\(L/2\) distancia de la pared. El agua tiene un caudal másico de\(150 \text{lbm} / \text{s}\), y la velocidad del agua es la misma entrando y saliendo de la pala,\(V_1 = V_2 = 20 \ \text{ft} / \text{s}\). El agua sale de la cuchilla en un ángulo\(30^{\circ}\) por debajo de la horizontal.

Otra información es la siguiente:\(L=5 \ \mathrm{ft}\),\(d=7 \ \mathrm{ft}\), y\(h=2 \ \mathrm{ft}\).

Determinar las reacciones en la viga en voladizo en la pared\((A)\).

Figura\(\PageIndex{4}\): El agua cae sobre una hoja curva unida a una viga en voladizo y sale del extremo inferior de la hoja.

Solución

Conocido: El agua es desviada por una pala soportada por una viga en voladizo.

Encuentra: Las reacciones en la viga voladiza en la pared.

Dado: Ver la figura anterior. Nuevamente, observe cómo todas las cantidades físicas tienen símbolos.

Análisis:

Estrategia\(\rightarrow\) Dado que se nos piden reacciones (fuerzas y momentos) debemos intentar utilizar la conservación del momento lineal y angular.

Sistema Sistema\(\rightarrow\) abierto, no deformante que incluye el agua de la hoja-viga con agua que fluye hacia dentro y hacia afuera como se muestra a continuación.
Propiedad para contar Momento\(\rightarrow\) angular y lineal (y posiblemente masa).
Intervalo de tiempo\(\rightarrow\) Probablemente un intervalo de tiempo infinitesimal, es decir, la forma de tasa.

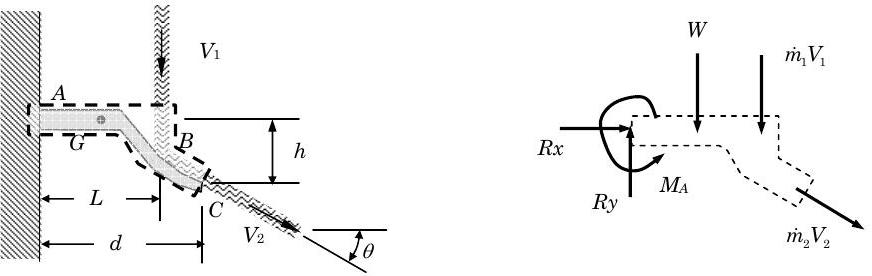
Figura\(\PageIndex{5}\): Diagrama de cuerpo libre de la viga, la pala y el sistema de agua.

La figura anterior muestra el diagrama de cuerpo libre (o interacción del sistema). Observe que la conexión en la pared es reemplazada por dos fuerzas y un momento porque la conexión de viga de pared es un soporte fijo. También tenga en cuenta que los transportes masivos de momento lineal se muestran en la figura junto con el peso que actúa en el punto\(G\).

Como punto de partida, escribamos la conservación de la masa y veamos qué nos dice:\[\underbrace{ \cancel{ \frac{d m_{\text{sys}}}{d t} }^{=0} }_{\text {steady state}} = \dot{m}_{1} - \dot{m}_{2} \quad \rightarrow \quad \dot{m}_{1} = \dot{m}_{2}=\dot{m} \nonumber \] Esto puede parecer un resultado trivial, pero si no lo viste de inmediato no es trivial. Además, esto solo confirma tu intuición.

Ahora escribamos la conservación del impulso lineal:\[ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{d t} }^{=0} = \mathbf{Rx} + \mathbf{Ry} + \mathbf{W} \ + \ \dot{m}_{1} \mathbf{V}_{1} - \dot{m} \mathbf{V}_{2} \quad \rightarrow \quad 0=\mathbf{Rx} + \mathbf{Ry} + \mathbf{W} \ + \ \dot{m}_{1} \mathbf{V}_{1} - \dot{m} \mathbf{V}_{2} \nonumber \]

Ahora escribiendo la forma escalar de esta ecuación, asumir positivo\(x\) está a la derecha y positivo\(y\) está arriba.

\[\begin{aligned} \boxed{\rightarrow +} \quad\quad 0 &= Rx - \dot{m}\left( V_{2} \cos \theta \right) \\ Rx &= \dot{m}\left( V_{2} \cos \theta \right) \quad \rightarrow \quad Rx = \left( 150 \ \dfrac{\mathrm{lbm}}{\mathrm{s}}\right) \left(20 \ \frac{\mathrm{ft}}{\mathrm{s}} \right) \left( \cos 30^{\circ} \right) \left(\frac{1 \ \mathrm{lbf}}{32.174 \ \dfrac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^{2}}} \right) = 80.8 \ \mathrm{lbf} \\ \\ \boxed{\uparrow +} \quad\quad 0 &= Ry - W + \dot{m}\left(-V_{1}\right) - \dot{m}\left(-V_{2} \sin 30^{\circ}\right) \\[4pt] Ry &= W + \dot{m}\left(V_{1}-V_{2} \sin 30^{\circ}\right) \\[4pt] &= W + \dot{m} V \left(1-\sin 30^{\circ}\right) \\[4pt] Ry &= \left[(100 \ \mathrm{lbm}) \left(\frac{1 \ \mathrm{slug}}{32.174 \ \mathrm{lbm}}\right) \left(32.174 \ \dfrac{\mathrm{ft}}{\mathrm{s}^{2}}\right) \right] \\[4pt] &=[100+46.6] \ \mathrm{lbf} \\[4pt] &=146.6 \ \mathrm{lbf} \end{aligned} \nonumber \]

Tenga mucho cuidado con las señales en los términos, especialmente los términos del caudal másico. Tenga\(+ \ / \ -\) en cuenta que el frente de los caudales másicos depende de si el flujo entra o sale del sistema; los signos dentro del paréntesis en los términos de velocidad (momento lineal específico) son el resultado de traducir el vector de velocidad a este sistema de coordenadas específico.

Con uno restante desconocido\(M_A\), necesitamos aplicar la conservación del momento angular. Aunque podemos sumar momentos sobre cualquier punto, usemos punto\(C\). Esto tiene el beneficio de eliminar el momento angular llevado a cabo en el chorro de agua en\(C\).

\[\begin{aligned} \frac{d \mathbf{L}_{C, \text{ sys}}}{d t} &= M_{A} + \left(\mathbf{r}_{A} \times \mathbf{Rx} \right) + \left( \mathbf{r}_{A} \times \mathbf{R y}\right) + \left(\mathbf{r}_{G} \times \mathbf{W}\right) + \dot{m} \left(\mathbf{r}_{B} \times \mathbf{V}_{1}\right) \\ \boxed{\mathrm{CW} +} \quad\quad 0 &= \left(-M_{A}\right) + (+h \cdot Rx) + (d \cdot Ry) + \left[ -\left(d-\dfrac{L}{2}\right) W \right] + \dot{m} \left[-(d-L) V_{1}\right] \\ M_{A} &= (h \cdot Rx) + (d \cdot Ry) + \left( -\left(d-\frac{L}{2}\right) W \right) + \dot{m}\left[-(d-L) V_{1}\right] \\ M_{A} &= [(2 \ \mathrm{ft})(80.8 \ \mathrm{lbf})] + [(7 \ \mathrm{ft})(146.6 \ \mathrm{lbf})] + \left[ -\left(7-\frac{5}{2}\right)(\mathrm{ft})(100 \ \mathrm{lbf}) \right] + \left(150 \ \frac{\mathrm{lbm}}{\mathrm{s}}\right) \left[-(2 \ \mathrm{ft})\left(20 \ \frac{\mathrm{ft}}{\mathrm{s}}\right) \right] \\ &=(161.6 \ \mathrm{ft} \cdot \mathrm{lbf}) + (1026.2 \ \mathrm{ft} \cdot \mathrm{lbf}) + (-450 \ \mathrm{ft} \cdot \mathrm{lbf}) + \underbrace{ \left(-6000 \ \frac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^2} \right) \left( \frac{1 \ \mathrm{lbf}}{32.174 \ \dfrac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^2}} \right) }_{= -186.5 \ \mathrm{ft} \cdot \mathrm{lbm}} \\ &=[161.6+1026.2-450-186.5] \ \mathrm{ft} \cdot \mathrm{lbf} \\ \\ M_{A} &= 551.3 \ \mathrm{ft} \cdot \mathrm{lbf} \end{aligned} \nonumber \]

Comentarios similares sobre los signos se aplican al momento angular dado para el momento lineal.

Así, las reacciones en\(A\) son\(Rx = 80.8 \ \mathrm{lbf}\)\(Ry =146.6 \ \mathrm{lbf}\), y\(M_{A} = 551.3 \ \mathrm{ft} \cdot \mathrm{lbf}\) en las direcciones como se indica en el diagrama.

Ejemplo — Volcar una caja

Se le ha pedido que ayude a mover un archivador empujándolo en el piso. Por suerte para ti el piso tiene coeficientes de fricción muy bajos (\(\mu_{\text {static}} = 0.3\)y\(\mu_{\text {kinetic}}=0.1\)). El archivador es\(0.3 \mathrm{~m}\) ancho y\(1.6 \mathrm{~m}\) alto y tiene una masa de\(100 \mathrm{~kg}\). Lo empujarás en una posición por encima del piso igual a\(3 / 4\) su altura.

(a) Determinar la fuerza\(F\) requerida para que el gabinete se mueva. ¿Empezará a dar propina antes de que se resbale?

b) Si se inclina antes de que resbale, ¿qué fuerza\(F\) se requiere para comenzar a volcar el gabinete estacionario?

(c) Si se desliza antes de que se incline, ¿cuál es la fuerza máxima\(F\) que se puede aplicar antes de que se deslice el gabinete?

Solución

Conocido: Un archivador está siendo empujado a lo largo del piso.

Encuentra:

(a) La fuerza requerida para deslizar el gabinete

(b) Si se inclina antes de resbalar, la fuerza requerida para comenzar a volcar

(c) Si se desliza antes de que se incline, la fuerza máxima que se puede aplicar antes de que se deslice el gabinete se inclina

Dado:\[\begin{aligned} &h=1.6 \mathrm{~m} \quad m=100 \mathrm{~kg} \\ &L=0.3 \mathrm{~m} \\ &d=1.2 \mathrm{~m} \\ &G \text { in center of rectangle } \\ \\ &\text {Positive directions on coordinate system } \end{aligned} \nonumber \]

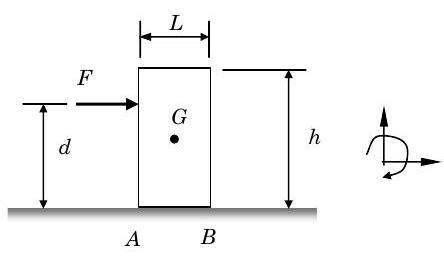
Figura\(\PageIndex{6}\): Diagrama etiquetado que muestra toda la información dada.

Análisis

Estrategia\(\rightarrow\) Intente conservar el momento lineal y angular ya que estamos considerando las fuerzas de fricción y el movimiento y vuelco.

Sistema Sistema\(\rightarrow\) cerrado, no deformante que incluye solo el gabinete.
Propiedad para contar Momento\(\rightarrow\) lineal e impulso angular.
Intervalo de tiempo\(\rightarrow\) Probablemente la forma de tasa ya que nos interesan las fuerzas.

Primero tenemos que dibujar el diagrama de cuerpo libre. Observe que la dirección de la fuerza de fricción a lo largo de la parte inferior del gabinete se opone al movimiento del gabinete. También debes notar que la fuerza normal\(F_{\mathrm{N}}\) en la parte inferior del gabinete puede actuar en cualquier lugar entre\(A\) y\(B\) dependiendo del valor de la fuerza aplicada\(F\). Claramente cuando\(F\) es cero la fuerza normal se aplica inmediatamente debajo del centro de masa.

Primero, determinemos qué fuerza hará que el gabinete se deslice. Para ello aplicamos la conservación del momento lineal a un sistema estacionario cerrado.

\[\underbrace{ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{dt} }^{=0} }_{ \begin{array}{c} \mathbf{P}=0 \\ \text{a constant} \end{array} } = \sum_{j} \mathbf{F}_{j} + \underbrace{ \cancel{ \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} }^{=0} }_{\text {closed system, no mass flow}} \quad \rightarrow \quad 0 = \mathbf{F} + \mathbf{F}_{f} + \mathbf{F}_{\mathrm{N}} +m \mathbf{g} \nonumber \]

Donde la fuerza de fricción debe ser igual a la fuerza máxima de fricción estática posible\[\begin{array}{lll} & \boxed{\rightarrow +} \quad & 0 =-F_{f}+F & \rightarrow \quad F=F_{f} \leq \mu_{\text {static}} F_{N} \\ & \boxed{\uparrow +} & 0=-m g+F_{N} & \rightarrow \quad F{N}=mg \\ & F=F_{f} \leq \mu_{\text {static}} m g = (0.3)\left[(100 \mathrm{~kg})\left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)\right] = 294.3 \mathrm{~N} \end{array} \nonumber \]

Por lo que la fuerza mínima que se debe aplicar para que el gabinete se deslice es\(294.3 \mathrm{~N}\).

Ahora para determinar si se inclina, aplique la conservación del momento angular al mismo sistema. Para ello hay que reconocer que justo en ella empieza a inclinarse (vuelco inminente) la fuerza normal está actuando en el punto\(B\) (el lado derecho del gabinete). Entonces calculemos el momento angular sobre el punto\(B\) y resolvamos para la fuerza que se debe aplicar para inclinar el gabinete asumiendo que es estacionario,\(F_{\text {tip}}\).

\[ \begin{array}{lll} & \underbrace{ \cancel{ \dfrac{d \mathbf{L}_{B, \text{ sys}}}{dt} }^{=0} }_{\begin{array}{c} \mathbf{L}=0 \text{ since} \\ \text{stationary} \end{array}} = \sum_j \mathbf{M}_{B, \ j} \ + \underbrace{ \cancel{ \sum - \sum}^{=0} }_{\begin{array}{c} \text{Closed system} \\ \text{No mass flow terms} \end{array}} \quad & \rightarrow \quad & 0 = \left( \mathbf{r}_F \times \mathbf{F}_{\text{tip}} \right) + \left( \mathbf{r}_G \times m \mathbf{g} \right) \\ \\ & \begin{align*} \boxed{\text{CW } +} \quad\quad 0 &= \left( d \ F_{\text{tip}} \right) + \left( \frac{L}{2} mg \right) \\ F_{\text{tip}} &= \frac{1}{2} \frac{L}{d} mg \end{align*} & \rightarrow & F_{\text{tip}} = \dfrac{1}{2} \left( \dfrac{0.3 \mathrm{~m}}{1.2 \mathrm{~m}} \right) (981.0 \mathrm{~N}) = 122.6 \mathrm{~N} \end{array} \nonumber \]

Comparando la fuerza para deslizarse contra la fuerza para inclinar, encontramos que la fuerza para inclinar es menor que la fuerza para deslizar el gabinete, el gabinete se inclina antes de que se deslice. La fuerza máxima que se puede aplicar al gabinete antes de que se incline es\(122.6 \mathrm{~N}\) y el gabinete nunca se deslizará.

La respuesta a la Parte c) es académica ya que el gabinete nunca resbala bajo estas condiciones.

Comentario:

Pero espera, ¡tenemos que mover el gabinete! Supongamos que colocamos el gabinete sobre algunos rodamientos de rodillos muy pequeños para que esencialmente se deslice sobre el piso sin fricción estática o cinética. ¿Cuánta fuerza puedo aplicar ahora antes de que se propine?

Los resultados\(y\) -momentum serán idénticos\(\rightarrow \ F_{\mathrm{N}} = mg = 981 \mathrm{~N}\).

Los resultados\(x\) -momentum deben considerar el movimiento en la\(x\) dirección así que tenemos\(\rightarrow m \frac{d V_{G}}{d t}=F\).

La ecuación de momento angular es más problemática. Primero debemos reconocer que el gabinete se está traduciendo, y que cuando el vuelco es inminente la fuerza normal\(F_{\mathrm{N}}\) actuará en la esquina derecha:

\[ \dfrac{d \mathbf{L}_{B}}{dt} = \left(\mathbf{r}_{F} \times \mathbf{F}\right) + \left(\mathbf{r}_{G} \times m \mathbf{g}\right) \quad \text { and } \quad \mathbf{L}_{B} = m \left(\mathbf{r}_{G} \times \mathbf{V}_{G}\right) \quad\quad\quad\quad\quad\quad\quad \nonumber \]

\[ \begin{align*} \boxed{ \text{CW }+ } \quad\quad \dfrac{d}{dt} \underbrace{ \left[ m \left( \dfrac{h}{2} V_G \right) \right] }_{\begin{array}{c} \text{Angular momentum} \\ \text{of system about} \\ \text{point }B \end{array}} &= \underbrace{ \left( d \ F \right) }_{\begin{array}{c} \text{Moment of} \\ \text{force } F \text{ about} \\ \text{point }B \end{array}} + \underbrace{ \left( - \dfrac{L}{2} mg \right) }_{\begin{array}{c} \text{Moment of} \\ \text{the weight about} \\ \text{point }B \end{array}} \\[4pt] m \dfrac{d}{dt} \left( \dfrac{h}{2} V_G \right) &= dF - \dfrac{L}{2} mg \\[4pt] m \dfrac{h}{2} \dfrac{d V_G}{dt} &= dF - \dfrac{L}{2} mg \quad\quad\quad \rightarrow \quad\quad\quad \begin{array}{l} \\{ } \\ F = \dfrac{m}{2} \dfrac{h}{d} \dfrac{d V_G}{dt} + \dfrac{m}{2} \dfrac{L}{2} g \\[4pt] F = \dfrac{m}{2} \left( \dfrac{h}{d} \right) \left[ \dfrac{d V_G}{dt} + g \left( \dfrac{L}{h} \right) \right] \end{array} \end{align*} \nonumber \]

Ahora necesitamos usar nuestros resultados del\(x\) -momentum para eliminar el término de aceleración\[\begin{aligned} F = \frac{m}{2} \left(\frac{h}{d}\right) \left[\frac{dV_{G}}{dt} + g \left(\frac{L}{h}\right) \right] &= \frac{m}{2}\left(\frac{h}{d}\right) \underbrace{\left[\left(\frac{F}{m}\right)+g\left(\frac{L}{h}\right)\right]}_{\begin{array}{c} \text { Here's where we } \\ \text { made the substitution } \end{array}} \\[4pt] \begin{array}{c} F - \dfrac{m}{2} \left(\dfrac{h}{d}\right) \left(\dfrac{F}{m}\right) = \dfrac{m}{2} \left(\dfrac{h}{d}\right) \left(\dfrac{L}{h}\right) g \\[4pt] F \left[1-\dfrac{1}{2}\left(\dfrac{h}{d}\right)\right] = \dfrac{m}{2} \left(\dfrac{L}{d}\right) g \\ { } \\ { } \end{array} \quad\quad\quad &\rightarrow \quad\quad\quad F = \dfrac{\dfrac{m}{2} \left(\dfrac{L}{d}\right) g}{\left[1-\dfrac{1}{2}\left(\dfrac{h}{d}\right)\right]} = (m g) \dfrac{\dfrac{1}{2} \left(\dfrac{L}{d}\right)}{\left[1-\dfrac{1}{2} \left(\dfrac{h}{d}\right)\right]} \end{aligned} \nonumber \]

Ahora sustituyendo los valores numéricos que tenemos\[F = (mg) \frac{\dfrac{1}{2}\left(\dfrac{L}{d}\right)}{\left[1 - \dfrac{1}{2} \left(\dfrac{h}{d}\right)\right]} =(981 \mathrm{~N}) \frac{\dfrac{1}{2}\left(\dfrac{0.3}{1.2}\right)}{\left[1 - \dfrac{1}{2} \left(\dfrac{1.6}{1.2}\right)\right]} = 367.9 \mathrm{~N} \nonumber \] Observe que el valor de\(F\) depende del peso del objeto, la relación\(h / d\), y la relación\(L / d\). ¿Qué pasa cuando\(d=h / 2\)? ¿Qué significa esto físicamente? ¿Y cuándo\(L=0\)? ¿Qué significa esto?

Ejemplo — ¡Está girando!

Dos cilindros metálicos\(A\) y\(B\) están suspendidos de una polea sin fricción. \(A\)El cilindro tiene una masa de\(30 \mathrm{~kg}\) y el cilindro\(B\) tiene una masa de\(60 \mathrm{~kg}\). La polea es esencialmente un disco plano con un diámetro de\(0.5 \mathrm{~m}\) y una masa de\(10 \mathrm{~kg}\). Los cables tienen una masa insignificante.

Figura\(\PageIndex{7}\): Dos cilindros suspendidos de una polea sin fricción.

Inicialmente los cilindros son estacionarios. Si se liberan repentinamente, calcule la aceleración de los cilindros.

Solución

Conocido: Dos masas suspendidas de una polea empiezan a moverse repentinamente.

Find: La aceleración de los cilindros después de que son liberados.

Dado: Ver la figura anterior.

\[ \begin{align*} & \text{Diameter of the pulley} = D = 0.5 \mathrm{~m}\\ & \text{Mass of the pulley} = m_{\text {Pulley}} = 10 \mathrm{~kg} \\ & \text{Mass of cylinder } A = m_{\mathrm{A}} = 30 \mathrm{~kg} \\ & \text{Mass of cylinder } B = m_{\mathrm{B}} = 60 \mathrm{~kg} \end{align*} \nonumber \]

Análisis:

Estrategia\(\rightarrow\) Prueba el momento angular ya que la polea está girando y no nos han dicho que ignoremos la masa de la polea.
Sistema Sistema\(\rightarrow\) cerrado que contiene los cilindros, el cable y la polea.
Propiedad para contar Momento\(\rightarrow\) angular Intervalo de
tiempo\(\rightarrow\) Inicio con ecuación de tasa

A continuación se muestra el diagrama de cuerpo libre, indicando las fuerzas conocidas en el sistema. Al tratarse de un sistema cerrado no hay transferencias masivas de impulso. Consulte las flechas en el diagrama para indicar las direcciones positivas para\(x_{A}, x_{B}\), y\(\omega\).

Figura\(\PageIndex{8}\): Diagrama de cuerpo libre del sistema que consiste en la polea y sus bloques unidos.

Escribiendo el momento angular alrededor del eje de rotación de la polea para el sistema y asumiendo que la rotación en sentido horario es positiva, tenemos el siguiente resultado:

\[\begin{aligned} \frac{d \mathbf{L}_{0, \text{ sys}}}{d t} &= \left(\mathbf{r}_{A} \times \mathbf{W}_{A}\right) + \left(\mathbf{r}_{B} \times \mathbf{W}_{B}\right) \\ \text{where} \quad\quad\quad \mathbf{L}_{0, \text{ sys}} &= m_{A} \left(\mathbf{r}_{A} \times \mathbf{V}_{A}\right) + m_{B} \left(\mathbf{r}_{B} \times \mathbf{V}_{B}\right) + \mathbf{\omega} I_{G} \\[4pt] \\ \boxed{\text{CW } +} \quad\quad \frac{d L_{0, \ \mathrm{sys}}}{d t} &= \left(\dfrac{D}{2} W_{B}\right) + \left(-\dfrac{D}{2} W_{A}\right) \\[4pt] \text{where} \quad\quad\quad L_{0, \mathrm{sys}} &= \underbrace{ \left(\dfrac{D}{2} m_{A} V_{A}\right) }_{\begin{array}{c} \text{Angular momentum of} \\ \text{Cylinder A about axle with} \\ \text{positive velocity } V_A \text{ upward} \end{array}} + \underbrace{ \left(\dfrac{D}{2} m_{A} V_{A}\right) }_{\begin{array}{c} \text{Angular momentum of} \\ \text{Cylinder B about axle with} \\ \text{positive velocity } V_B \text{ downward} \end{array}} + \underbrace{ \omega I_{G} }_{\begin{array}{c} \text{Angular momentum of} \\ \text{the pulley assuming positive} \\ \omega \text{ is in clockwise direction} \end{array}} \end{aligned} \nonumber \]

Ahora sustituyendo el momento angular del sistema en el balance de momento que tenemos

\[ \boxed{\mathrm{CW} \ +} \quad\quad \frac{d}{dt} \left[ \left(\frac{D}{2} m_{A} V_{A}\right) + \left(\frac{D}{2} m_{A} V_{A}\right) + \omega I_{G}\right] = \left(\frac{D}{2} W_{B}\right) + \left(-\frac{D}{2} W_{A}\right) \nonumber \]

Esta ecuación puede simplificarse aún más reconociendo que solo las velocidades son constantes, por lo que llevar las constantes fuera de la derivada y dividirlas por\(D / 2\) da lo siguiente\[\boxed{\mathrm{CW} \ +} \quad\quad m_{A} \frac{d V_{A}}{d t} + m_{B} \frac{d V_{B}}{d t} + \left(\frac{2}{D}\right) I_{G} \frac{d \omega}{d t} = -W_{A}+W_{B} \nonumber \]

Para ir más allá, debemos relacionar las velocidades traslacional y rotacional. Suponiendo que una dirección rotacional positiva es en sentido horario que corresponde con las flechas de velocidad en el diagrama, tenemos lo siguiente:\[V_{A} = V_{B} = \omega (D / 2) \nonumber \] Usando este resultado para reemplazar\(V_{\text {В }}\) y\(\omega\) en el balance de momento angular da lo siguiente:

\[\begin{aligned} \boxed{\mathrm{CW} \ +} \quad\quad m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{B}}{dt} + \left(\frac{2}{D}\right) I_{G} \frac{d}{dt} \left(\frac{2}{D} V_{A}\right) &= W_{B}-W_{A} \\[4pt] m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{A}}{dt} + \left(\frac{2}{D}\right)^{2} I_{G} \frac{d V_{A}}{d t} &= W_{B}-W_{A} \end{aligned} \nonumber \]

Para terminar, debemos escribir los pesos y el momento de inercia de masa de la polea en términos de su masa de la siguiente manera:

\[\begin{aligned} m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{A}}{dt} + \left(\frac{2}{D}\right)^{2} I_{G} \frac{d V_{A}}{dt} &= W_{B}-W_{A} \\[4pt] m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{B}}{dt} + \left(\frac{2}{D}\right)^2 \underbrace{ \left[\frac{1}{2} m_{\text {Pulley }} \left(\frac{D}{2}\right)^{2}\right] }_{\begin{array}{c} I_G \text{ for the pulley treated} \\ \text{as a disk} \end{array}} \frac{d V_A}{dt} &= m_B \ g - m_A \ g \\ m_A \frac{d V_A}{dt} + m_B \frac{d V_A}{dt} + \left( \frac{m_{\text{Pulley}}}{2} \right) \left[\frac{d V_A}{dt}\right] &= \left(m_B - m_A\right) g \\[4pt] \frac{d V_A}{dt} &= \frac{ \left(m_B - m_A\right) }{\left(m_A + m_B + \dfrac{m_{\text{Pulley}}}{2}\right)} g \end{aligned} \nonumber \]

Sustituir en los números da\[\frac{d V_{A}}{dt} = \frac{\left(m_{B}-m_{A}\right)}{\left(m_{A} + m_{B} + \frac{m_{\text {Pulley}}}{2}\right)} g = \frac{(60-30)}{\left(30+60+\dfrac{10}{2}\right)} g = \left(\frac{30}{95}\right) g = 3.098 \ \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber \]

Así\(A\) el cilindro acelera hacia arriba y\(B\) el cilindro acelera hacia abajo a la velocidad de\(3.098 \mathrm{~m} / \mathrm{s}^{2}\).

Comentario:

Determinar el error si hubiéramos descuidado la masa de la polea: es decir, ¿cuál sería la aceleración si hubiéramos descuidado la masa de la polea?