7.1: Mecánica y Balance Energético Mecánico

Históricamente, el principio de conservación general de la energía fue uno de los últimos principios identificados por la comunidad científica. Sin embargo, las formas restringidas del principio se derivaron anteriormente de otros principios fundamentales. Uno de los más útiles es el balance energético mecánico. En esta sección, demostraremos cómo se puede desarrollar este equilibrio a partir de la conservación del impulso lineal. En el camino, presentaremos varios conceptos nuevos —como el trabajo mecánico, la potencia mecánica y la energía mecánica— que están enraizados en el estudio de la mecánica.

7.1.1 Trabajo Mecánico y Potencia Mecánica

Al principio de nuestro estudio de conservación del impulso lineal examinamos diferentes formas de escribir la tasa de cambio de tiempo del momento lineal para una partícula:\[\frac{d}{d t}(m V) = m \frac{d V}{d t} = m \left(\frac{d V}{d x}\right) \left(\frac{d x}{d t}\right) = m\left[V \frac{d V}{d x}\right] \nonumber \] La motivación para este ejercicio fue la necesidad de integrar la ecuación de impulso lineal cuando la información solo se dio en función de la posición única \(x\). Esta misma preocupación nos lleva a considerar la integral de una fuerza con posición.

Trabajo Mecánico

Figura\(\PageIndex{1}\): Fuerza superficial que actúa sobre el límite de un sistema.

El trabajo mecánico realizado por una fuerza superficial\(\mathbf{F}\) que actúa sobre el límite de un sistema (ver Figura\(\PageIndex{1}\)) es la integral\[W_{\text {mech}} \equiv \int\limits_{\mathbf{s}_{1}}^{\mathbf{s}_{2}} \mathbf{F} \cdot d \mathbf{s} = \int\limits_{1}^{2} \delta W_{\text {mech}} \quad \text { where } \delta W_{\text {mech}} \equiv \mathbf{F} \cdot d \mathbf{s} \nonumber \] donde\(d \mathbf{s}\) se encuentra el vector de desplazamiento diferencial del punto de aplicación de la fuerza sobre el límite y\(\mathbf{s}_{1}\) y\(\mathbf{s}_{2}\), respectivamente, son los posiciones inicial y final del límite.

Figura\(\PageIndex{2}\): Evaluación del trabajo mecánico diferencial,\(\delta W_{\text {mech}}\).

Para comprender mejor esta integral, es útil examinar la cantidad diferencial de trabajo\(\delta W_{\text {mech}}\). Para ayudar, la Figura\(\PageIndex{2}\) muestra tanto la fuerza\(\mathbf{F}\) como el desplazamiento\(d \mathbf{s}\). Tenga en cuenta que la fuerza se\(\mathbf{F}\) puede descomponer en dos componentes:\(\mathbf{F}_{\perp}\) normal a\(d \mathbf{s}\) y\(\mathbf{F}_{\text {tan}}\) tangente a\(d \mathbf{s}\). Usando la definición de un producto punto entre dos vectores, tenemos el siguiente resultado para\(\delta W_{\text {mech}}\):

\[ \begin{align} \delta W_{\text{mech}} &= \mathbf{F} \cdot d \mathbf{s} = |\mathbf{F}| |d \mathbf{s}| \cos \theta = F \cdot ds \cdot \cos \theta \nonumber \\[4pt] &= F \cdot \underbrace{ \left[ ds \cdot \cos \theta \right] }_{\begin{array}{c} \text{Component of displacement} \\ \text{that is parallel to the } \\ \text{force's line of action} \end{array}} = \underbrace{ \left[ F \cdot \cos \theta \right] }_{\begin{array}{c} \mathbf{F}_{\text{tan }} = \text{ Component of the force} \\ \text{that is parallel to the} \\ \text{displacement's line of action} \end{array}} \end{align} \nonumber \]

De la Eq. \(\PageIndex{2}\)arriba, vemos que existen dos interpretaciones distintas para la cantidad diferencial de trabajo. \(\delta W_{\text {mech}}\)puede interpretarse como (1) el producto de la fuerza y el componente del desplazamiento que es paralelo a la fuerza o (2) el producto del desplazamiento y el componente de la fuerza que es paralelo al desplazamiento.

Se pueden descubrir varios puntos adicionales sobre el trabajo mecánico mediante un examen minucioso de la integral, la Ec. \(\PageIndex{1}\):

• El trabajo mecánico es una cantidad escalar; sin embargo, es una cantidad firmada porque el producto punto\(\mathbf{F} \cdot d \mathbf{s}\) puede ser positivo o negativo dependiendo del ángulo\(\theta\) entre los vectores (Ver Figura\(\PageIndex{2}\))
• Las dimensiones del trabajo mecánico son\([\text{Force}] [\text{L}]\) o\([\text{M}] [\text{L}]^{2} [\text{T}]^{-2}\)
• Las unidades para el trabajo están\(\text{N} \cdot \text{m}\) en SI y\(\text{ft} \cdot \text{lbf}\) en el sistema USCS. El hecho de que un conjunto de unidades sea fuerza-longitud y el otro sea longitud-fuerza es arbitrario y probablemente el resultado de lo que sonó bien al oído.
• El trabajo integral y por lo tanto mecánico solo puede evaluarse si se conocen los estados finales y la trayectoria del proceso que conecta estos estados. Matemáticamente, se debe conocer\(\mathbf{F}\) en función de la posición\(\mathbf{s}\) para evaluar la integral.
• El trabajo mecánico de un sistema no se puede evaluar en un estado específico o en un momento específico. Sólo se puede evaluar para un proceso —un cambio de estado. El trabajo mecánico es un ejemplo de una función de trayectoria porque su integral definitoria, la Ec. \(\PageIndex{1}\), sólo se puede evaluar cuando se conoce el camino del proceso. Esto contrasta, digamos, con el problema de encontrar el cambio de volumen para un proceso. Para encontrar el cambio en el volumen de un sistema, solo necesitamos conocer el volumen del sistema en cada estado final sin tener en cuenta la trayectoria del proceso. Así, el volumen, como todas las propiedades de un sistema, es una función de estado (o punto).

Pon a prueba tu comprensión — ¿Cuál es el trabajo?

(a)\(\mathbf{F}=F \mathbf{i} \quad\) y de\(\quad \mathbf{s}=x \mathbf{i} + y \mathbf{j}\) dónde\(x=a t\) y\(y=b t\) de\(t_{1}\) a\(t_{2}\)\[\begin{aligned} W_{\text {mech}} &= \int\limits_{\mathbf{s}_{1}}^{\mathbf{s}_{2}} \mathbf{F} \cdot d \mathbf{s} = \int\limits_{1}^{2}(F \mathbf{i}) \cdot (d x \mathbf{i}+d y \mathbf{j}) = \int\limits_{1}^{2} \left[ \underbrace{ (F \mathbf{i}) \cdot(d x \mathbf{i}) }_{\mathbf{i} \cdot \mathbf{i}=1} + \underbrace{ (F \mathbf{i}) \cdot(d y \mathbf{j}) }_{\mathbf{i} \cdot \mathbf{j}=0} \right] \\ &= \int\limits_{x_{1}}^{x_{2}} F \ dx \quad \text { but } \quad dx =adt \\ &= \int\limits_{t_{1}}^{t_{2}}(F a) \ dt = F a\left(t_{2}-t_{1}\right) \end{aligned} \nonumber \] Obsérvese que aunque el punto de aplicación se mueva en la\(\mathbf{j}\) dirección, no hay componente de la fuerza\(\mathbf{F}\) en esa dirección y el único trabajo lo realiza el componente de la fuerza en la\(\mathbf{i}\) dirección.

b)\(\mathbf{F}=F_{x} \mathbf{i}+F_{y} \mathbf{j} \quad\) y\(\quad \mathbf{s}=x \mathbf{i}+y \mathbf{j} \quad\) de\(\mathbf{s}_{1}\) a\(\mathbf{s}_{2} \quad\) si\(y=x^{2}\)\[\begin{aligned} W_{\text {mech}} &= \int\limits_{\mathbf{s}_{1}}^{\mathbf{s}_{2}} \mathbf{F} \cdot d \mathbf{s} = \int\limits_{1}^{2} \left(F_{x} \mathbf{i}+F_{y} \mathbf{j}\right) \cdot \left[ (dx)\mathbf{i} + (dy)\mathbf{j} \right] = \int\limits_{x_{1}}^{x_{2}} \underbrace{ \left[ \left(F_{x} \cdot d x\right) + \left(F_{y} \cdot d y\right)\right] }_{\mathrm{i} \cdot \mathbf{j} = \mathbf{j} \cdot \mathbf{i} =0 \text { and } \mathbf{i} \cdot \mathbf{i} = \mathbf{j} \cdot \mathbf{j} = 1} \\ &= \int\limits_{1}^{2} \left[\left(F_{x} \cdot d x\right) + \left(F_{y} \cdot \underbrace{d y}_{d y=2x \ dx}\right) \right] \\ &= \int\limits_{x_{1}}^{x_{2}} \left[F_{x} + \left(2x \cdot F_{y}\right)\right] \ dx = F_{x}\left(x_{2}-x_{1}\right) + F_{y} \underbrace{ \left(x_{2}^{\ 2} - x_{1}^{\ 2}\right) }_{=\left(y_{2}-y_{1}\right)} \end{aligned} \nonumber \]

Poder Mecánico

La tasa de tiempo a la que la fuerza superficial\(\mathbf{F}\) funciona en el sistema se denomina potencia mecánica y se define por la ecuación\[\dot{W}_{\text {mech}} \equiv \mathbf{F} \cdot \mathbf{V} \nonumber \] donde\(\mathbf{V}\) está la velocidad del punto de aplicación de la fuerza\(\mathbf{F}\) en el límite del sistema.

Al integrar la potencia mecánica con respecto al tiempo en un intervalo de tiempo finito, podemos demostrar la relación entre la potencia mecánica y el trabajo mecánico:\[\int\limits_{t_{1}}^{t_{2}} \dot{W}_{\text {mech}} \ dt = \left\{ \begin{array}{l} \int\limits_{t_{1}}^{t_{2}} (\mathbf{F} \cdot \mathbf{V}) \ dt = \int\limits_{t_{1}}^{t_{2}} \left(\mathbf{F} \cdot \frac{d \mathbf{s}}{d t}\right) \ dt = \int\limits_{t_{1}}^{t_{2}} \underbrace{\mathbf{F} \cdot d \mathbf{s}}_{\delta W_{\text{mech}}} = W_{\text {mech}} \\ \int\limits_{1}^{2} \delta W_{\text {mech}} = W_{\text {mech}} \quad \text { where } \quad \delta W_{\text {mech}}=\dot{W}_{\text {mech}} dt \end{array}\right. \nonumber \] Tenga en cuenta que la integral de\(\delta W_{\text {mech}}\) no es igual\(\Delta W_{\text {mech}}\).

Se deben hacer varios puntos adicionales sobre la potencia mecánica y su relación con el trabajo mecánico:

• La potencia mecánica, a diferencia del trabajo mecánico, se puede evaluar en un momento específico porque es la velocidad instantánea a la que se realiza el trabajo.
• Las dimensiones para la potencia mecánica son\([\mathrm{Force}][\mathrm{L}] /[\mathrm{T}]\) o\([\mathrm{M}][\mathrm{L}]^{2}[\mathrm{T}]^{-3}\).
• Las unidades de potencia mecánica están\(\mathrm{N} \cdot \mathrm{m} / \mathrm{s}\) en SI\(\mathrm{ft} \cdot \mathrm{lbf} / \mathrm{s}\) y/o\(\mathrm{hp}\) (caballos de fuerza) en USCS. (\(1 \mathrm{hp}=550 \mathrm{ft} \cdot \mathrm{lbf} / \mathrm{s}\), aproximadamente).

Antes de salir de la discusión sobre el trabajo mecánico y la potencia mecánica, tenga en cuenta que tienen definiciones muy precisas y pueden, dada la suficiente información, ser evaluadas a partir de sus ecuaciones definitorias. Ahora investigamos cómo nuestro conocimiento de la potencia mecánica y el trabajo pueden ayudarnos a resolver algunos problemas de la mecánica usando escalares en lugar de vectores.

7.1.2 El principio trabajo-energía

El principio trabajo-energía es el vínculo directo entre la conservación del impulso lineal y el equilibrio energético mecánico. Se desarrolla aquí primero para una partícula y luego se expande para incluir un sistema de partículas.

Principio de trabajo-energía para una partícula

Considerar el movimiento de una partícula de masa\(m\) en un campo gravitacional. (Recordemos que una partícula es un sistema con su masa concentrada en un punto que sólo puede traducirse a medida que se mueve a través del espacio, es decir, su momento de inercia de masa es cero.) Como se muestra en la Figura\(\PageIndex{3}\), el vector de posición\(\mathbf{s}\) describe la posición de la partícula. Las únicas fuerzas externas que actúan sobre la partícula son el peso\(\mathbf{W}\) y las fuerzas de superficie neta (o contacto)\(\mathbf{R}\). Tenga en cuenta que el vector de gravedad actúa en la dirección del\(z\) eje negativo.

Figura\(\PageIndex{3}\): Movimiento de una partícula en un campo gravitacional.

Si aplicamos la conservación del impulso lineal a la partícula que tenemos\[\frac{d \mathbf{P}_{\mathrm{sys}}}{dt} = \mathbf{R}+\mathbf{W} \quad \rightarrow \quad m \frac{d \mathbf{V}_{G}}{dt} = \mathbf{R}+m \mathbf{g} \nonumber \] donde hemos reconocido que una partícula es un sistema cerrado, su momento lineal es\(\mathbf{P}_{\text {sys}} = m \mathbf{V}_{G}\), y su peso lo es\(m \mathbf{g}\).

Ahora evaluemos la potencia mecánica suministrada a la partícula por la fuerza de contacto\(\mathbf{R}\). Dado que la partícula es un punto, la fuerza\(\mathbf{R}\) se mueve con la velocidad\(\mathbf{V}_{G}\) y el trabajo mecánico es\[\dot{W}_{\text {mech}} = \mathbf{R} \cdot \mathbf{V}_{G} \nonumber \] Para eliminar la fuerza superficial\(\mathbf{R}\), utilizamos los resultados de la conservación del momento lineal, Eq. \(\PageIndex{5}\), de la siguiente manera:\[\begin{array}{l} \dot{W}_{\text {mech}} &= \mathbf{R} \cdot \mathbf{V}_{G} = \left[m \dfrac{d \mathbf{V}_{G}}{dt} - m \mathbf{g}\right] \cdot \mathbf{V}_{G} \\ &= \underbrace{m \dfrac{d \mathbf{V}_{G}}{d t} \cdot \mathbf{V}_{G} }_{\text {Inertia term}} - \underbrace{m \mathbf{g} \cdot \mathbf{V}_{G}}_{\text {Gravitation Term}} \end{array} \nonumber \] Hemos identificado un “término de inercia” y un “término de Gravitación” en el lado derecho de la Eq. \(\PageIndex{7}\). Antes de continuar, necesitamos investigar estos dos términos.

El término de inercia en la Ec. \(\PageIndex{7}\)es el producto puntual de la velocidad de la partícula con la velocidad de cambio del momento lineal de la partícula. Comenzando con el término de inercia y realizando el producto punto, tenemos

\[\begin{array}{l} \left[ \begin{array}{c} \text {Inertia} \\ \text {term} \end{array}\right] &= m \dfrac{d \mathbf{V}_{G}}{d t} \cdot \mathbf{V}_{G}=\dfrac{m}{2} \dfrac{d}{dt} \left(\mathbf{V}_{G} \cdot \mathbf{V}_{G}\right) \\ &= \dfrac{m}{2} \dfrac{d}{dt} \left(V_{G}{ }^{2}\right) = \dfrac{d}{dt} \left(m \dfrac{V_{G}{ }^{2}}{2}\right) = \dfrac{d E_{K}}{dt} \\ \text { where } E_{K} & \equiv m \dfrac{V_{G}{ }^{2}}{2}=\text { the kinetic energy of a particle } \end{array} \nonumber \]

Así, el término de inercia es solo la derivada ordinaria de una cantidad escalar a la que normalmente nos referimos como la energía cinética de la partícula. Debido a que la energía cinética solo depende de las propiedades del sistema y también depende de la masa del sistema, la energía cinética es una propiedad extensa.

De igual manera, podemos masajear el término de gravitación. Para ello, nos referimos de nuevo a Figura\(\PageIndex{3}\) y primero escribimos la velocidad y el término peso usando los vectores unitarios\(\mathbf{i}\),\(\mathbf{j}\), y\(\mathbf{k}\). Luego realizamos el producto punto de la siguiente manera:\[\begin{array}{l} \left[\begin{array}{c} \text {Gravitation} \\ \text { term } \end{array}\right] &= m \mathbf{g} \cdot \mathbf{V}_{G} = m(-g \mathbf{k}) \cdot \left(V_{G, \ x} \mathbf{i} + V_{G, \ y} \mathbf{j} + V_{G, \ z} \mathbf{k}\right) \\ &= -mg \left[ V_{G, \ x} \underbrace{ \left(\mathbf{k} \cdot \mathbf{i} \right) }_{=0} + V_{G, \ y} \underbrace{ \left(\mathbf{k} \cdot \mathbf{j}\right) }_{=0} + V_{G, \ z} \underbrace{ \left(\mathbf{k} \cdot \mathbf{k}\right)}_{=1} \right] \\ &= -mg V_{G, \ z} = -mg\left(\dfrac{dz}{dt}\right) \quad \text { because } V_{G, \ z}=\dfrac{dz}{dt} \\ &= -\dfrac{d}{dt}(m g z) = -\dfrac{d E_{GP}}{dt} \\ \text{where } E_{G P} & \equiv m g z= \text{the gravitational potential energy of a particle.} \end{array} \nonumber \]

Así, el término de inercia es proporcional a la derivada ordinaria de otro escalar típicamente denominado energía potencial gravitacional de la partícula. Con frecuencia esto se abrevia como “energía potencial”. Basada en un argumento análogo al de la energía cinética, la energía potencial gravitacional es una propiedad extensa.

Usando estos nuevos términos de energía, podemos reescribir la ecuación para la potencia mecánica suministrada a la partícula por la fuerza de contacto\(\mathbf{R}\), la Ec. \(\PageIndex{7}\), según se indica:

\[\begin{align} \dot{W}_{\text {mech}} = \mathbf{R} \cdot \mathbf{V}_{G} &= \underbrace{ m \frac{d \mathbf{V}_{G}}{d t} \cdot \mathbf{V}_{G} }_{\text{Inertia term}} - \underbrace{ m \mathbf{g} \cdot \mathbf{V}_{G} }_{\text{Gravitational term}} \nonumber \\ &=\left[\dfrac{d}{dt} \left(m \dfrac{V_{G}^{2}}{2}\right)\right] - \left[-\dfrac{d}{dt}(m g z)\right] \\[4pt] \dot{W}_{\text {mech}} &= \dfrac{d E_{K}}{dt} + \dfrac{d E_{G P}}{dt} \nonumber \end{align} \nonumber \]

Esta es la forma de velocidad del principio trabajo-energía para una partícula. Es una ecuación muy potente y útil cuando se aplica correctamente. En palabras esta ecuación dice:

La potencia mecánica suministrada por las fuerzas superficiales netas a una partícula que se mueve en un campo gravitacional es igual a la tasa de cambio temporal de la energía cinética y la energía potencial gravitacional de la partícula.

Frecuentemente, la forma de tiempo finito es útil. Para obtener esta forma, integramos ambos lados de la Eq. \(\PageIndex{10}\)durante un intervalo de tiempo finito de la siguiente manera:\[\begin{align} \int\limits_{t_{1}}^{t_{2}} \dot{\mathbf{W}}_{\text {mech}} \ dt &= \int\limits_{t_{1}}^{t_{2}} \left[\frac{d E_{K}}{dt} + \frac{d E_{G P}}{dt}\right] \ dt \nonumber \\ \int_{t_{1}}^{t_{2}} \delta W_{\text {mech}} &= \int\limits_{1}^{2} d E_{K} + \int\limits_{t_{1}}^{t_{2}} d E_{G P} \\ W_{\text {mech}} &= \underbrace{ \left(E_{K, \ 2}-E_{K, \ 1}\right) }_{=\Delta E_{K}} +\underbrace{ \left(E_{GP, \ 2}-E_{GP, \ 1}\right)}_{=\Delta E_{GP}} \nonumber \end{align} \nonumber \]

Esta ecuación es la forma de tiempo finito del principio de trabajo-energía para una partícula. En palabras, esta ecuación dice

El trabajo mecánico realizado por las fuerzas superficiales netas sobre una partícula que se mueve en un campo gravitacional equivale al cambio de la energía cinética y la energía potencial gravitacional de la partícula.

Observe cómo ambas ecuaciones involucran solo términos escalares, en comparación con la conservación de la ecuación de impulso lineal con la que comenzamos. Antes de continuar, recapitulemos los pasos que usamos para derivar el principio trabajo-energía:

• Escribimos la forma de tasa de conservación del momento lineal para una partícula que se mueve en un campo gravitacional y separamos las fuerzas externas en dos grupos: la fuerza de gravedad (una fuerza corporal) y las fuerzas superficiales.
• Escribimos la potencia mecánica suministrada por las fuerzas superficiales a la partícula.
• Se utilizaron los resultados de la conservación del momento lineal para reemplazar el término de fuerza superficial en la expresión de potencia mecánica.
• Evaluamos los términos de inercia y gravitación (los términos de producto punto) por separado e identificamos dos nuevas propiedades extensas: energía cinética y energía potencial gravitacional.
• Finalmente, reescribimos la ecuación para el poder mecánico en términos de la tasa de cambio temporal de la energía cinética y potencial gravitacional de la partícula.

Tenga en cuenta que esto fue de hecho una derivación que comienza con la conservación del impulso lineal. Debido a esto, el principio de trabajo-energía no aporta nada nuevo a nuestro análisis sobre lo que aprendemos aplicando la conservación del impulso lineal. Sin embargo, su naturaleza escalar a menudo la convierte en una alternativa útil a la conservación del impulso lineal, que por su propia naturaleza es una relación vectorial.

Principio de trabajo-energía para un sistema de partículas

Debido a que nuestra derivación del principio trabajo-energía fue solo para una sola partícula, uno podría preguntarse si es aplicable a sistemas compuestos por varias partículas. Para investigar esta pregunta, considere el siguiente ejemplo de dos bloques que se deslizan sobre un plano.

Ejemplo — Aplicación del principio trabajo-energía a un sistema de dos partículas

Considera un sistema que consta de dos bloques, Bloques\(A\) y\(B\), apilados inicialmente como se muestra en la figura. El bloque\(A\) descansa sobre el bloque\(B\). La superficie de contacto entre\(A\) y\(B\) es rugosa, con coeficiente de fricción cinética\(\mu_{\mathrm{k}}\) y coeficiente de fricción estática\(\mu_{\mathrm{s}}\). El bloque\(B\) descansa sobre una superficie horizontal lisa y se desliza libremente sobre la superficie sin fricción. De repente\(\mathbf{F}\) se aplica una fuerza al bloqueo\(A\) y ambos bloques comienzan a moverse.

Figura\(\PageIndex{4}\): Un sistema que consta de dos bloques unidos por fricción.

Para estudiar las limitaciones del principio trabajo-energía, determinar la tasa de cambio de la energía cinética de los bloques después de aplicar\(\mathbf{F}\) la fuerza. Compare sus resultados usando dos sistemas de partículas únicas y usando un sistema combinado que incluya ambas partículas.

Para hacer uso del principio trabajo-energía, primero debemos identificar claramente todas las fuerzas externas que actúan sobre el sistema. Esto se hace a continuación para el Sistema\(A B\)\(A\), Sistema y Sistema\(B\).

Sistema\(AB\)

Sistema\(A\)

Sistema\(B\)

Figura\(\PageIndex{5}\): Diagramas de cuerpo libre para sistemas que constan de bloques\(AB\), de\(A\) solo bloque y de\(B\) solo bloque.

Para el sistema\(A\), el principio trabajo-energía se puede escribir como\[\begin{aligned} \frac{d}{dt} \left(E_{K}+E_{G P}\right)_{A} &= \dot{W}_{\text {mech}} \\ \frac{d E_{K, \ A}}{dt} + \underbrace{ \cancel{ \frac{d E_{GP, \ A}}{dt} }^{=0} }_{\text {No change in elevation}} &= \left(\mathbf{F} \cdot \mathbf{V}_A\right) + \underbrace{ \cancel{ \left(\mathbf{F}_{NA} \cdot \mathbf{V}_A\right) }^{=0} }_{\begin{array}{c} \text{Force and velocity} \\ \text{are perpendicular} \end{array}} + \underbrace{ \left(\mathbf{F}_f \cdot \mathbf{V}_A\right) }_{\text{Friction}} \\ \frac{dE_{K, \ A}}{dt} &= \left(F \cdot V_A\right) + \underbrace{ \left(-F_f \cdot V_A\right) }_{\begin{array}{c} \text{Friction force opposes} \\ \text{motion with velocity } V_A \end{array}} \quad \rightarrow \quad \boxed{ \frac{d}{dt} \left(m_A \frac{V_A ^{\ 2}}{2} \right) = \left( F - F_f \right) \cdot V_A } * \end{aligned} \nonumber \]

Observe cómo para el sistema\(B\), el principio de trabajo-energía se puede escribir como\[\begin{aligned} \frac{d}{dt} \left(E_K + E_{GP}\right)_B &= \dot{W}_{\text{mech}} \\ \frac{d E_{K, \ B}}{dt} + \underbrace{ \cancel{\frac{d E_{GP, \ B}}{dt}}^{=0} }_{\text{No change in elevation}} &= \underbrace{ \cancel{ \left(\mathbf{F}_N \cdot \mathbf{V}_B\right) }^{=0} }_{\begin{array}{c} \text{Force and velocity} \\ \text{are perpendicular} \end{array}} + \underbrace{ \cancel{ \left(\mathbf{F}_{NA} \cdot \mathbf{V}_B\right) }^{=0} }_{\begin{array}{c} \text{Force and velocity} \\ \text{are perpendicular} \end{array}} + \underbrace{ \left(\mathbf{F}_f \cdot \mathbf{V}_B\right) }_{\text{Friction}} \\ \frac{d E_{K, \ B}}{dt} &= \left(F_f \cdot V_B\right) \quad \rightarrow \quad \boxed{ \frac{d}{dt} \left( m_B \frac{V_B ^{\ 2}}{2} \right) = \left(F_f \cdot V_B\right) } ** \end{aligned} \nonumber \]

donde la velocidad utilizada en el cálculo de la potencia mecánica debe ser la velocidad del bloque\(B\) basada en nuestra derivación del principio trabajo-energía para una partícula.

Ahora sumando estas dos ecuaciones, tenemos\[ \begin{aligned} \left. \begin{array}{c} \dfrac{d}{dt} \left(m_{A} \dfrac{V_{A}{ }^{2}}{2}\right) = \left(F-F_{f}\right) \cdot V_{A} \\ + \\ \dfrac{d}{dt} \left(m_B \dfrac{V_{B}{ }^{2}}{2} \right) = F_f \cdot V_B \end{array} \right\} \quad \rightarrow \quad & \frac{d}{dt} \left(m_A \frac{V_{A}{ }^{2}}{2}\right) + \frac{d}{dt} \left(m_B \frac{V_{B}{ }^{2}}{2} \right) = \left(F-F_f\right) \cdot V_A + F_f \cdot V_B \\ & \boxed{ \ \underbrace{ \frac{d}{dt} \left(m_A \frac{V_{A}{ }^{2}}{2}\right) + \frac{d}{dt} \left(m_B \frac{V_{B}{ }^{2}}{2}\right) }_{\begin{array}{c} \text{Rate of change of the kinetic energy} \\ \text{of blocks } A \text{ and } B \end{array}} = F \cdot V_A - \left(F_f\right) \cdot \left(V_A - V_B\right) \ }*** \end{aligned} \nonumber \]

Para System\(A B\), las únicas fuerzas de contacto son\(\mathbf{F}_{N}\), la fuerza normal ejercida por el suelo sobre el bloque\(B\), y\(\mathbf{F}\), la fuerza horizontal aplicada al bloque\(A\). Suponiendo que es válido escribir el principio de energía de trabajo para dos partículas como un solo sistema, escribimos

\[\begin{aligned} \frac{d \left(E_{K}+E_{G P}\right)_{sys}}{dt} &= \dot{W}_{\text {mech}} \\ \frac{d}{dt} \left[ \left(E_{K}+E_{GP}\right)_{A} + \left(E_{K}+E_{GP}\right)_{B} \right] &= \left(\mathbf{F} \cdot \mathbf{V}_{A}\right) + \underbrace{ \cancel{ \left(\mathbf{F}_{B} \cdot V_{B}\right) }^{=0} }_{\begin{array}{c} \text{Force normal} \\ \text{to velocity} \end{array}} \\ \frac{d E_{K, \ A}}{dt} + \cancel{ \frac{d E_{GP, \ A}}{dt} }^{=0} + \frac{d E_{K, \ B}}{dt} + \cancel{ \frac{d E_{GP, \ B}}{dt} }^{=0} &= F \cdot V_{A} \quad \rightarrow \quad \boxed{ \frac{d}{dt} \left(m_{A} \frac{V_{A}{ }^{2}}{2}\right) + \frac{d}{dt}\left(m_{B} \frac{V_{B}{ }^{2}}{2}\right) = F \cdot V_{A} } * * * * \end{aligned} \nonumber \]

Si el principio trabajo-energía se aplica a sistemas con dos partículas, entonces la Ec. \({***}\)y Eq. \(^{* * * *}\)debería darnos la misma información. ¿En qué condiciones son idénticas estas dos ecuaciones?

Condición 1: La fuerza de fricción es cero.

Condición 2: No hay velocidad relativa entre las partículas, es decir\(V_{A}=V_{B}\). Así parecería que el principio trabajo-energía describe con precisión el comportamiento de un sistema con múltiples partículas solo bajo un conjunto limitado de condiciones.

Así parecería que el principio trabajo-energía describe con precisión el comportamiento de un sistema con múltiples partículas solo bajo un conjunto limitado de condiciones.

Afortunadamente, experiencias como la anterior nos permiten establecer lineamientos generales para el uso del principio trabajo-energía:

El principio trabajo-energía se puede aplicar a cualquier sistema cerrado si (1) el sistema puede modelarse como una colección de partículas, es decir, el momento de inercia de cada subsistema es insignificante, y (2) no hay fricción dentro del sistema.

Como veremos en breve, estas limitaciones están relacionadas con el hecho de que el principio trabajo-energía es una aplicación restringida del principio de conservación general de la energía. Ahora pasaremos a una aplicación del principio trabajo-energía:

Ejemplo — Movin' boxes

Dos cajas descansan sobre planos inclinados individuales y están conectadas por una polea como se muestra en la figura. La masa de cada caja es\(12 \mathrm{~kg}\) y las cajas descansan sobre superficies sin fricción. Si el sistema se libera del reposo, determine la magnitud de la velocidad de los pesos cuando se hayan movido una distancia\(L=1 \mathrm{~m}\) a lo largo de los planos.

Figura\(\PageIndex{6}\): Una polea en la intersección de dos planos inclinados soporta una cuerda conectada a cajas en cada plano.

Solución

Conocido: Dos cajas conectadas por polea y cable deslizan sobre superficies inclinadas.

Encuentra: La velocidad de las cajas cuando han recorrido una distancia de a\(1 \mathrm{~m}\) lo largo de los aviones.

Dado: Ver la figura anterior.

Estrategia\(\rightarrow\) Existen al menos tres formas posibles de intentar este problema. Una es aplicar la conservación del impulso lineal. Un segundo es aplicar la conservación del momento angular. Un tercero es probar el principio trabajo-energía. (Esto es, en realidad, solo una forma alternativa de aplicar la conservación del impulso lineal).

Sistema\(\rightarrow\) Ambos bloques, la polea, el cable y el soporte de la polea.
Propiedad a contar\(\rightarrow\) Probemos energía mecánica, es decir, principio de trabajo-energía.
Intervalo de tiempo\(\rightarrow\) Comienza con la forma de tiempo finito ya que tenemos un desplazamiento finito.

Primero debemos esbozar el diagrama de cuerpo libre e identificar todas las fuerzas externas que actúan sobre nuestro sistema. Si miras con atención verás los pesos de las dos cajas, las fuerzas normales sobre las dos cajas, dos fuerzas donde cortamos el soporte de la polea, y el peso de la polea y su soporte. (Mira la figura y encuentra cada una de estas.) También verás la\(z\) coordenada positiva que apunta opuesta a la dirección de la gravedad.

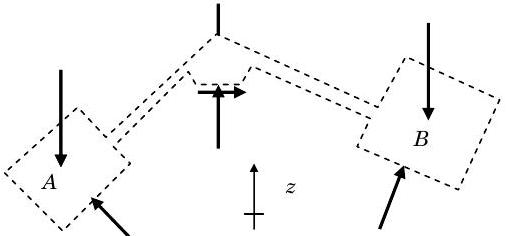
Figura\(\PageIndex{7}\): Diagrama de cuerpo libre del sistema que consiste en las cajas, su cable de conexión y la polea alrededor de la cual envuelve el cable.

Ahora para aplicar el principio de trabajo-energía a este sistema, debemos modelar el sistema cerrado como una colección de partículas sin fricción interna.

\[ \begin{align*} \Delta \left(E_K + E_{GP}\right)_{sys} &= W_{\text{mech}} \\ \Delta E_K + \Delta E_{GP} &= \underbrace{ \cancel{ W_{\text{mech}} }^{=0} }_{\begin{array}{c} \mathbf{F} \cdot d\mathbf{s}=0 \text{ for all} \\ \text{contact forces} \end{array}} \\ \Delta \left(m_A \dfrac{V_{A}{ }^{2}}{2} + m_B \frac{V_{B}{ }^{2}}{2}\right) + \Delta \left(m_A gz_A + m_B gz_B\right) &= 0 \\ \underbrace{ \left(m_A \frac{V_{A}{ }^{2}}{2} + m_B \frac{V_{B}{ }^{2}}{2}\right)_2 }_{\begin{array}{c} V_A=V_B=V \text{ since connected} \\ \text{by inextensible cable} \end{array}} + \left(m_A gz_A + m_B gz_B\right)_2 &= \underbrace{ \cancel{ \left(m_A \frac{V_{A}{ }^{2}}{2} + m_B \frac{V_{B}{ }^{2}}{2}\right) }^{=0} }_{\text{Initially stationary, no velocity}} + \left(m_A gz_A + m_B gz_B\right)_1 \\[4pt] \left(m_A + m_B\right) \frac{V_{2}{ }^{2}}{2} &= m_A g \left(z_1 - z_2\right)_A + m_B g \left(z_1 - z_2\right)_B \end{align*} \nonumber \]

Al desarrollar esta ecuación también hemos asumido que no hay fricción dentro del sistema y la rotación de la polea es insignificante, es decir, tiene un momento de inercia de masa despreciablemente pequeño alrededor de su eje de rotación.

Observe cuidadosamente que la fuerza de gravedad, o el peso de las masas, no hace ningún trabajo en el sistema. Incluir el peso como fuerza en el término de trabajo es un error común y resulta en un doble conteo del efecto de la gravedad. Ignorar el efecto de la gravedad en el término de trabajo es una consecuencia directa de nuestra definición de trabajo mecánico en términos de fuerzas superficiales (de contacto). Podemos manejar el efecto de la gravedad de dos maneras diferentes. Si incluimos la fuerza de la gravedad en el término de trabajo, no hay energía potencial gravitacional. Si manejamos el efecto de la gravedad a través del término de energía potencial gravitacional, entonces solo las fuerzas superficiales funcionan. Para ser congruentes con el principio general de conservación de la energía, hemos optado por utilizar este último enfoque.

Para ir más allá, debemos indicar cómo se relaciona el cambio de elevación con el desplazamiento de las cajas a lo largo de los planos. Supongamos que la caja\(A\) sube por el avión y la caja\(B\) se mueve hacia abajo del avión.

Por lo tanto\[\left(z_{2}-z_{1}\right)_{A} = L \sin \theta \quad \text { and } \quad \left(z_{2}-z_{1}\right)_{B}=-L \sin \alpha \nonumber \]

Sustituyendo esto de nuevo en el resultado del principio trabajo-energía, tenemos\[\begin{aligned} \left(m_{A}+m_{B}\right) \frac{V_{2}{ }^{2}}{2} &= m_{A} g\left(z_{1}-z_{2}\right)_{A} + m_{B} g\left(z_{1}-z_{2}\right)_{B} \\ &= -m_{A} g\left(z_{2}-z_{1}\right)_{A} - m_{B} g\left(z_{2}-z_{1}\right)_{B} \\ &=-m_{A} g(L \sin \theta) - m_{B} g(-L \sin \alpha) \quad \text { but } \quad m_{A}=m_{B}=m_{Box} \\ \left(2 m_{box} \right) \frac{V_{2}{ }^{2}}{2} &= m_{box} g L(\sin \alpha-\sin \theta) \\[4pt] V^{2} &= g L(\sin \alpha-\sin \theta) = \left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) (1 \mathrm{~m}) \left(\sin 30^{\circ}-\sin 45^{\circ}\right) = -2.032 \ \frac{\mathrm{m}^{2}}{\mathrm{~s}^{2}} \end{aligned} \nonumber \]

¿Qué pasó? ¿Cómo podemos tomar la raíz cuadrada de un número negativo? ¿Significa esto que tenemos una velocidad compleja? Ten mucho cuidado cuando te encuentres ante tomar la raíz cuadrada de un número negativo. Casi siempre significa que algo está en error, ya que una velocidad compleja no tiene ningún significado físico en este problema.

¡Lo que pasó es que adivinamos mal sobre la dirección original del movimiento! Si hubiéramos asumido que la caja\(A\) se movió por el avión y la caja\(B\) se movió hacia arriba por la colina nuestras ecuaciones para\(\Delta z\) en términos de\(L\) habrían tenido signos opuestos y\[\begin{aligned} \left(m_{A}+m_{B}\right) \frac{V_{2}{ }^{2}}{2} &= -m_{A} g\left(z_{2}-z_{1}\right)_{A} - m_{B} g\left(z_{2}-z_{1}\right)_{B} \\ &= -m_{A} g(-L \sin \theta)-m_{B} g(L \sin \alpha) \quad \text { but } \quad m_{A}=m_{B}=m_{Box} \\ \left(2 m_{box}\right) \frac{V_{2}{ }^{2}}{2} &= m_{box} g L(-\sin \alpha+\sin \theta) \\ V^{2} &= g L(\sin \theta-\sin \alpha) = \left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) (1 \mathrm{~m}) \left(\sin 45^{\circ}-\sin 30^{\circ}\right) = 2.032 \ \frac{\mathrm{m}^{2}}{\mathrm{s}^{2}} \\ V &=1.43 \ \frac{\mathrm{m}}{\mathrm{s}} \text { where the elevation of } B \text{ increases and the elevation of } A \text{ decreases.} \end{aligned} \nonumber \]

Formar un punto de vista energético lo que esto significa es que el aumento de la energía cinética proviene de una disminución en la energía potencial gravitacional total del sistema. La disminución en la energía potencial gravitacional de la caja\(A\) equivale al aumento de la energía potencial gravitacional de la caja\(B\) más el aumento de la energía cinética de todo el sistema.

Comentario:

(a) Para verificar esta respuesta, intente usar uno de los otros métodos.

(b) ¿Cómo cambiaría su respuesta si el coeficiente de fricción cinética para la superficie\(B\) fuera\(0.1\)? [Ans:\(V=1.09 \mathrm{~m} / \mathrm{s}\)]

7.1.3 El balance energético mecánico

Es útil en este punto aplicar lo que sabemos sobre el concepto contable para entender mejor el principio trabajo-energía. Si empezamos con la forma de tasa, la Ec. \(\PageIndex{10}\)y reorganizarlo para que las derivadas estén en el lado izquierdo, tenemos la siguiente ecuación:\[\frac{d}{dt} \left(E_{K}+E_{G}\right) = \dot{W}_{\text {mech}} \nonumber \] Debido a que la energía cinética y la energía gravitacional son ambas propiedades extensas, podemos aumentar nuestra comprensión de la Eq. \(\PageIndex{12}\)examinándolo a la luz del marco contable.

Para esta ecuación, la propiedad extensa es la energía mecánica del sistema. Debido a sus raíces en la mecánica, la energía cinética y la energía potencial gravitacional se denominan colectivamente energía mecánica. Si el lado izquierdo de la Ec. \(\PageIndex{12}\)representa la tasa de cambio de una propiedad extensa del sistema, entonces el lado derecho debe representar ya sea una tasa de transporte o tasa de generación. Debido a que la potencia mecánica se define en términos de una fuerza y velocidad en el límite, nos referiremos a la potencia mecánica como una tasa de transporte de energía mecánica.

En términos de energía mecánica, la forma de tasa del principio trabajo-energía, Ec. \(\PageIndex{12}\), puede interpretarse de la siguiente manera:

La tasa de tiempo de cambio (o acumulación) de energía mecánica de un sistema es igual a la tasa neta de transporte de energía mecánica al sistema por trabajo mecánico.

Desafortunadamente, no existe un principio físico general que siempre satisfaga esta afirmación. Sin embargo, si nos limitamos a la energía mecánica y solo consideramos aquellos casos en los que no hay destrucción o generación de energía mecánica, entonces la Eq. \(\PageIndex{12}\)es el balance energético mecánico sin generación ni destrucción de energía mecánica.

Un análisis más general demostraría que en la mayoría de las condiciones, la energía mecánica solo puede ser destruida dentro de un sistema. Piensa en lo que sucede cuando dejas caer una pelota de golf al suelo y la dejas rebotar hasta que deje de moverse. Ahora suponga que hizo este experimento en un vacío para eliminar la fricción del aire. Inicialmente, la pelota de golf tiene energía potencial gravitacional y no tiene energía cinética. Cuando termina de rebotar y descansa sobre el suelo, tiene menos energía potencial gravitacional y no tiene energía cinética. ¿A dónde fue la energía mecánica inicial? Veremos más adelante que se convierte irreversiblemente en energía interna —la energía del movimiento de los átomos y moléculas del sistema.

A veces Eq. \(\PageIndex{12}\)se llama la “conservación de energía mecánica” para un sistema cerrado. Por favor, ten cuidado si quieres pensar en estos términos. En este curso, normalmente reservamos la palabra “conservación” para un uso general, describiendo cómo funciona siempre el mundo. Como demostraremos posteriormente utilizando el principio de conservación general de la energía, la Ec. \(\PageIndex{12}\)se restringe a un sistema adiabático cerrado donde el trabajo mecánico es el único mecanismo de trabajo para transportar energía, y la energía solo se puede almacenar como energía mecánica. Vea cuántos calificadores hay que agregar solo para llegar a “conservación de energía mecánica” desde el principio general de conservación de energía.

7.1.4 Una Energía Mecánica Adicional — Energía de Primavera

Si piensas en tu clase de física, estudiaste manantiales ideales. Para nuestros propósitos, un resorte ideal es aquel que sigue la misma curva de fuerza-desplazamiento independientemente de la dirección de desplazamiento del extremo del resorte, es decir, un resorte sin histéresis. Una de las primeras cosas que aprendiste es que la fuerza requerida para comprimir o extender un resorte se describe por la ecuación:\[F_{\text {spring}}=k x \nonumber \] donde\(k\) esta la constante del resorte con unidades\(\mathrm{N} / \mathrm{m}\)\(\mathrm{lbf} / \mathrm{in}\) o o\(\mathrm{lbf} / \mathrm{ft}\) y\(x\) es el desplazamiento del extremo del resorte desde su descargado o posición de longitud libre.

Figura\(\PageIndex{8}\): Un resorte ideal.

Ahora considere un bloque de masa\(m\) sobre una superficie horizontal, sin fricción, como se muestra en la Figura\(\PageIndex{9}\). Inicialmente el bloque se sujeta contra el resorte, y el resorte se comprime a una longitud\(L\). La longitud libre del resorte es\(L_{o}\). De pronto se suelta el bloque y el bloque se mueve hacia la derecha. ¿Cómo podríamos usar el balance de energía mecánica para resolver la velocidad del bloque?

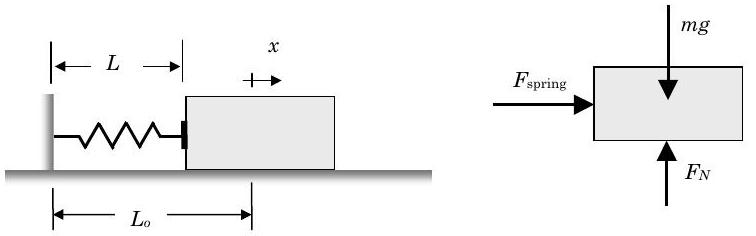
Figura\(\PageIndex{9}\): Fuerzas que actúan sobre un bloque debido a un resorte en expansión.

Primero seleccionamos el bloque como nuestro sistema y dibujamos un diagrama de cuerpo libre que muestra todas las fuerzas externas que actúan sobre nuestro sistema (ver Figura\(\PageIndex{9}\)). Preste especial atención a la ubicación del sistema\(x\) de coordenadas. A continuación asumiremos que el bloque se puede modelar como una partícula y podemos aplicar la forma de tiempo finito del balance energético mecánico:

\[\begin{array}{ll} \Delta E_{K} & +\underbrace{ \cancel{ \Delta E_{G P} }^{=0} }_{\text{No change in elevation}} &= W_{\text {mech}} = \int\limits_{\mathbf{s}_{1}}^{\mathbf{s}_{2}} \mathbf{F} \cdot d \mathbf{s} = \int\limits_{x_{1}}^{x_{2}} F_{\text {spring}} \cdot dx \\ & \frac{m}{2}\left(V_{2}{ }^{2}-V_{1}{ }^{2}\right) &= \int\limits_{x_{1}}^{x_{2}} \left[k\left(L_{o}-L\right)\right] \cdot dx \quad \text { where } \quad L=L_{o}+x \\ & &= \int\limits_{x_{1}}^{x_{2}} \left[k\left(L_{o}-\left(L_{o}+x\right)\right)\right] \cdot dx \\ & &= \int_{x_{1}}^{x_{2}}[-k x] \cdot dx = -\frac{k}{2}\left(x_{2}{ }^{2}-x_{1}{ }^{2}\right) \end{array} \nonumber \]

Con la longitud comprimida inicial del resorte\(L_{1}\), la velocidad en cualquier ubicación se\(x_{2}\) puede desarrollar a partir del resultado anterior de la siguiente manera:\[\begin{gathered} \frac{m}{2} \left(V_{2}{ }^{2}-\underbrace{V_{1}{ }^{2}}_{=0}\right) = -\frac{k}{2}\left[x_{2}{ }^{2}-x_{1}{ }^{2}\right] = -\frac{k}{2}\left[x_{2}{ }^{2}-\left(L_{1}-L_{o}\right)^{2}\right] \\ m \frac{V_{2}{ }^{2}}{2} = \frac{k}{2}\left[\left(L_{1}-L_{o}\right)^{2}-x_{2}{ }^{2}\right] \\[4pt] V_{2} = \sqrt{\frac{k}{m} \left[\left(L_{1}-L_{o}\right)^{2} - x_{2}{ }^{2}\right]} \end{gathered} \nonumber \]

Pon a prueba tu comprensión

Como comprobación del resultado, considere lo que sucede con la velocidad del bloque si\(L_{1}=L_{o}\).

¿Cuál es la velocidad máxima del bloque y dónde ocurre?

¿Cuál es la posición del bloque cuando la velocidad va a cero?

Ahora volvamos a la Eq. \(\PageIndex{14}\)y reorganizar ese resultado:

\[\begin{array}{l} &\frac{m}{2} \left(V_{2}{ }^{2}-V_{1}{ }^{2}\right) = -\frac{k}{2}\left(x_{2}{ }^{2}-x_{1}{ }^{2}\right) \\ &\underbrace{\frac{m}{2}\left(V_{2}{ }^{2}-V_{1}{ }^{2}\right)}_{=\Delta E_{K}} + \underbrace{\frac{k}{2}\left(x_{2}{ }^{2}-x_{1}{ }^{2}\right)}_{=\Delta E_{\text {spring}}}=0 \end{array} \nonumber \]

Observe que el término en el lado izquierdo sólo depende de los estados finales del sistema. Esto es característico de una propiedad y de hecho ambas cantidades en el lado izquierdo son cambios en propiedades extensas del sistema. El primero es nuestro viejo amigo el cambio en la energía cinética. El segundo término es nuevo y se llama el cambio en la energía primaveral (elástica) del sistema. Definimos la energía de resorte (elástica) del sistema como:\[E_{\text {spring}} \equiv \frac{1}{2} k x^{2} \nonumber \]

El resorte ideal almacena energía en la deformación elástica del resorte con la cantidad de energía directamente relacionada con la compresión o expansión del resorte desde su longitud descargada o libre.

Figura\(\PageIndex{10}\): Analizando un sistema con el resorte dentro del sistema.

Si tratáramos la energía del resorte como una forma de energía mecánica y hubiéramos colocado el resorte dentro de nuestro sistema (ver Figura\(\PageIndex{10}\)), el balance de energía mecánica sin pérdidas se vería como el siguiente para el sistema de bloque de resorte:\[\Delta E_{K} + \Delta E_{G P} + \Delta E_{\text {spring}}=W_{\text {mech}} \nonumber \] Para resolver el problema, nuevamente calcularíamos el\(W_{\text {mech}}\) para el sistema; sin embargo, ninguna de las fuerzas externas contribuye al trabajo mecánico. La fuerza normal no contribuye porque es perpendicular al movimiento; el peso no contribuye porque es una fuerza corporal y no una fuerza superficial; y la fuerza de soporte que sujeta el resorte a la pared no se mueve. Así, la ecuación energética se reduciría de la siguiente manera:

\[\begin{array}{c} \underbrace{\Delta E_{K}}_{V_{1}=0} + \underbrace{ \cancel{\Delta E_{G P}}^{=0} }_{\text {No change in elevation}} + \Delta E_{\text {spring}} = \cancel{ W_{\text {mech}} }^{=0} \\ \Delta E_{K}+\Delta E_{\text {spring}} = 0 \\ m \frac{V_{2}^{2}}{2}+\frac{k}{2}\left(x_{2}{ }^{2}-x_{1}{ }^{2}\right)=0 \end{array} \nonumber \]

Este resultado es idéntico a la Ec. \(\PageIndex{14}\), el resultado obtenido cuando el resorte estaba fuera del sistema; sin embargo, el enfoque actual es más sencillo porque no se realizó ningún trabajo en el sistema. Desde una perspectiva de energía mecánica, lo que está sucediendo aquí es que la energía inicial almacenada en el resorte se convierte en la energía cinética del bloque repetidamente a medida que el bloque oscila de un lado a otro. Esta oscilación continuará para siempre a menos que haya fricción interna al sistema o fricción entre el bloque y la superficie horizontal.

En la sección actual, hemos ampliado nuestra definición de energía mecánica para incluir la energía cinética, la energía potencial gravitacional y ahora la energía de resorte (o elástica). Esto por sí solo sería de poca consecuencia, excepto que también hemos afirmado que esta nueva energía puede incluirse dentro de nuestro balance energético mecánico existente. Esta experiencia de etiquetar o identificar una nueva forma de energía y luego encajarla en un marco existente es característica del desarrollo histórico del principio de conservación de la energía. Ahora vamos a pasar a este principio más general, la conservación de la energía —uno de los principios más poderosos y generalizados de la física y la ciencia de la ingeniería.