7.8: Almacenamiento y transferencia de energía eléctrica

Por su importancia y su singularidad, necesitamos echar un vistazo más de cerca a la transferencia y almacenamiento de energía eléctrica. Como inicio, ¿a qué nos referimos exactamente con energía eléctrica? Para nuestros propósitos, definiremos la energía eléctrica como la energía que se almacena en un campo eléctrico o magnético. Nuestro énfasis aquí será considerar cómo se aplica el principio de conservación de energía a los dispositivos y sistemas que se encuentran comúnmente en los dispositivos eléctricos y electrónicos. Nos limitaremos a sistemas que puedan modelarse utilizando elementos de circuito agrupados (como se discute en la Sección 4.3 del Capítulo 4).

7.8.1 Potencia instantánea y media

Anteriormente en este capítulo, desarrollamos una ecuación para la energía eléctrica en términos del flujo de una corriente eléctrica a través del sistema y la diferencia de potencial eléctrico en los terminales donde la corriente entra y sale del sistema. En nuestro desarrollo anterior, asumimos tácitamente que la corriente y los voltajes eran independientes del tiempo. En realidad, sabemos que casi toda nuestra energía eléctrica se suministra en forma de una corriente alterna variable en el tiempo. El comportamiento transitorio de los circuitos eléctricos también es de interés en el diseño de todo, desde sistemas de energía hasta sistemas de control y computadoras. En esta sección, abordaremos el problema de calcular la alimentación de CA.

Figura\(\PageIndex{1}\): Sistema de dos terminales para trabajo eléctrico y potencia.

Energía Eléctrica Instantanea

Para propósitos de nuestra discusión, nos limitaremos a un sistema de dos terminales como se muestra en la Figura\(\PageIndex{1}\). La corriente eléctrica\(i\) fluye al sistema en un terminal con voltaje\(V_{\text {in-o}}\) y sale del sistema en un terminal con voltaje\(V_{\text {out-o}}\). Ambos voltajes se miden con respecto al mismo punto de tierra (punto\(O\)). Además, asumiremos que los voltajes y la corriente pueden cambiar con el tiempo. Bajo estas condiciones, nuestra expresión anterior de energía eléctrica sigue siendo válida; pero representa la energía eléctrica instantánea para un sistema:\[\begin{array}{ll} \dot{W}_{\text {electric, in}} & =i \cdot\left(V_{\text {in-o}}-V_{\text {out-o}}\right) \quad & \\ &= i \cdot \Delta V & \text { Instantaneous Electric Power } \end{array} \nonumber \] Por convención, la energía eléctrica instantánea es positiva cuando la corriente ingresa al sistema en el terminal con el voltaje más alto y negativo cuando sale del sistema en el terminal con el voltaje más alto.

En un sistema de CC (corriente continua), la potencia instantánea es una constante e independiente del tiempo; así, la energía eléctrica instantánea también es constante e independiente del tiempo.

En un sistema de CA (corriente alterna), la corriente\(i\) y la diferencia de voltaje\(\Delta V\) para los terminales se pueden describir como funciones sinusoidales del tiempo:\[\Delta V=V_{\max } \cos (\omega t) \quad \text { and } \quad i = i_{\max } \cos (\omega t+\theta) \nonumber \] donde\(\omega\) esta la frecuencia\((\mathrm{rad} / \mathrm{s})\),\(t\) es el tiempo\((\mathrm{s})\) y\(\theta\) es el angulo de fase (radianes) que describe cómo la corriente conduce o retarda el voltaje\([-\pi / 2 \leq \theta \leq \pi / 2]\). El periodo de un ciclo depende de la frecuencia de la siguiente manera:\[2 \pi=\omega \cdot t_{\text {period}} \quad \rightarrow \quad t_{\text {period}}=\frac{2 \pi}{\omega} \nonumber \]

Bajo estas condiciones, la potencia instantánea se calcula de la siguiente manera:\[\begin{array}{l} \dot{W}_{\text {electric, in}} &= i \cdot \Delta V = \left[i_{\max } \cos (\omega t)\right] \cdot\left[V_{\max } \cos (\omega t+\theta)\right] \\ &=i_{\max } \cdot V_{\max } \cdot \cos (\omega t) \cdot \cos (\omega t+\theta) \\ &=i_{\max } \cdot V_{\max } \cdot \dfrac{1}{2} \cdot[\cos (2 \omega t+\theta)+\cos (\theta)] \end{array} \nonumber \] donde se obtiene la última línea aplicando una relación trigonométrica estándar para multiplicar cosenos. Antes de dejar esta expresión es útil separar la potencia instantánea, la Ec. \(\PageIndex{4}\), en dos partes:\[\begin{array}{l} \dot{W}_{\text {electric, in}} &= i_{\max } \cdot V_{\max } \cdot \dfrac{1}{2} \cdot [\cos (2 \omega t+\theta)+\cos (\theta)] \\ &=\underbrace{\dfrac{i_{\max } \cdot V_{\max }}{2} \cos (\theta)}_{\begin{array}{c} \text {Time-independent} \\ \text{component} \end{array}} + \underbrace{\dfrac{i_{\max } \cdot V_{\max }}{2} \cos (2 \omega t+\theta)}_{\begin{array}{c} \text{Time-varying periodic} \\ \text{component} \end{array}} \end{array} \nonumber \] La primera parte es independiente del tiempo y sólo depende del ángulo de fase\(\theta\), mientras que el segundo componente varía periódicamente con el tiempo. Un examen cuidadoso de la Ec. \(\PageIndex{5}\)muestra que la potencia de CA instantánea es una función sinusoidal que oscila entre cero y un valor máximo (o pico) de\(i_{\max} \cdot V_{\max} \cdot \cos(\theta)\).

Energía Eléctrica Promedio

La potencia eléctrica promedio se define como la cantidad de energía eléctrica transferida a través de un límite dividida por el intervalo de tiempo durante el cual se produce la transferencia. Matemáticamente, la potencia eléctrica promedio para un intervalo de tiempo se\(t_{\mathrm{obs}}\) puede calcular a partir de la ecuación\[\dot{W}_{\text {avg, in}} = \frac{1}{t_{\text {obs}}} \int\limits_{0}^{t_{\text {obs}}} \dot{W}_{\text {electric, in}} \ dt \nonumber \] Si el voltaje y la corriente son constantes como serían en un sistema de CC, la potencia promedio y la potencia instantánea son idénticas. En un sistema de CA, la potencia promedio se calcularía a lo largo del período de tiempo para un ciclo de la potencia instantánea (o dos ciclos de la tensión y la corriente) de la siguiente manera:\[\begin{aligned} \dot{W}_{\text {avg, in}} &= \frac{1}{t_{\text {obs}}} \int\limits_{0}^{t_{\text {obs}}} \dot{W}_{\text {electric, in}} \ dt \quad \text { where } \quad\quad\quad t_{\text {obs}}=t_{\text {period}}=\frac{2 \pi}{2 \omega}=\frac{\pi}{\omega} \\ &=\frac{1}{t_{\text {period}}} \int\limits_{0}^{t_{\text {period}}}\left[\frac{i_{\max } \cdot V_{\max }}{2} \cos (\theta)\right] dt \quad\quad\quad \left| \begin{array}{l} \text { What happened to the } \\ \text { time-varying component? } \end{array} \right. \\ &=\frac{1}{t_{\text {period}}}\left[\frac{i_{\max } \cdot V_{\max }}{2} \cos (\theta)\right] t_{\text {period}} = \frac{i_{\max } \cdot V_{\max }}{2} \cos (\theta) \end{aligned} \nonumber \]

Esto finalmente da\[\dot{W}_{\text {avg, in}} = \frac{1}{2} i_{\max } \cdot V_{\max } \cdot \cos (\theta) \quad\quad\quad \begin{array}{c} \text {Average} \\ \text{AC electric power} \end{array} \nonumber \] Así se puede calcular la potencia promedio conociendo los valores máximos (o picos) para la tensión de corriente y el ángulo\(\theta\). Tenga en cuenta, que la constante numérica de\(1 / 2\) depende de la forma de las señales de voltaje y corriente y no de la frecuencia específica. Si las señales de voltaje y corriente tuvieran una forma diferente, como una onda en diente de sierra o una onda cuadrada, la constante numérica cambiaría.

7.8.2 Alimentación CA y Voltaje y Corriente Efectiva

¿A qué nos referimos exactamente cuando decimos 110 voltios ac? ¿Es este el voltaje máximo (o pico)? ¿Es el promedio? Pero el promedio no tendría ningún sentido porque el promedio de una sinusoide que oscila alrededor de cero es cero. Puede parecerle extraño, pero alguna vez hubo una época en la que la energía eléctrica se distribuía utilizando voltajes y corrientes de CC. Desafortunadamente para Thomas Edison, quien promovió la distribución de CC, los sistemas de CA ganaron la victoria. No obstante, el fantasma de la CC aún vive en la forma en que hablamos de voltajes y corrientes de CA. Resulta que el voltaje y la corriente de CA se reportan en términos de sus valores efectivos que están relacionados con un equivalente de CC que entregaría la misma potencia promedio a una resistencia.

El valor efectivo de una corriente de CA\(i_{\text {eff}}\) es igual al valor de una corriente de CC que entregaría la misma potencia promedio a una resistencia de carga. La relación entre la corriente AC máxima y el valor efectivo de la corriente AC se desarrolla a continuación.

\[ \begin{aligned} \left. \dot{W}_{\text{electric, in}} \right|_{average, \ DC} \ &= \ \left. \dot{W}_{\text{electric, in}} \right|_{average, \ AC} \\ i_{\text{eff}}{ }^{2} \cancel{ R_{\text{load}} } &= \frac{1}{t_{\text{period}}} \int\limits_{0}^{t_{\text{period}}} i^2 \cancel{ R_{\text{load}} } \ dt = \frac{1}{t_{\text{period}}} \int\limits_{0}^{t_{\text{period}}} \left[i_{\max} \cos (\omega t + \theta) \right]^{2} \cancel{ R_{\text{load}} } \ dt \end{aligned} \nonumber \]

\[\begin{aligned} i_{\text {eff}}{ }^{2} &= i_{\max }{ }^{2} \left\{\frac{1}{t_{\text {period}}} \int\limits_{0}^{t_{\text {period}}} [\cos (\omega t+\theta)]^{2} \ dt\right\} \\ &=i_{\max }{ }^{2} \left\{\frac{1}{t_{\text {period}}} \int\limits_{0}^{t_{\text {period}}} \left[\frac{1}{2}+\frac{1}{2} \cos (2 \omega t+2 \theta)\right] \ dt \right\} \\ &=\left\{\frac{1}{t_{\text {period}}} \left[\frac{1}{2}\left(t_{\text {period}}-0\right)+0\right]\right\}^{2} = \frac{i_{\max }{ }^{2}}{2} \end{aligned} \nonumber \]Así tenemos el resultado final:\[i_{\text {eff}} = \frac{i_{\max }}{\sqrt{2}} \quad \text { Effective AC current } \nonumber \]

Si la corriente variable en el tiempo tuviera una forma de onda diferente a una sinusoide, digamos una onda cuadrada o una onda en diente de sierra, la constante en el numerador tomaría un valor diferente.

De manera similar, el valor efectivo de una tensión de CA\(V_{\text {eff}}\) es igual al valor de una tensión de CC que entregaría la misma potencia promedio a una resistencia de carga. Usando un desarrollo similar al de la corriente efectiva, descubrimos que:\[V_{\text {eff}} = \frac{V_{\max }}{\sqrt{2}} \quad \text { Effective AC voltage } \nonumber \] Y esta es la respuesta a la pregunta con la que empezamos — ¿qué es un\(110 \mathrm{AC}\) voltaje? Los 110 voltios son el valor efectivo de la\(\mathrm{AC}\) tensión. Entonces en un osciloscopio, una señal de 110-Ca-Volt sería una sinusoide con un valor máximo\(V_{\max }=110 \cdot \sqrt{2}=155.6\) voltios. Una señal de 220-Ca-Volt tendría un valor máximo de\(311.1\) voltios.

Ahora bien, si revisamos la ecuación para la potencia de CA promedio, podemos reescribirla en términos de los valores efectivos:\[\begin{array}{l} \dot{W}_{\text {avg, in}} &=\dfrac{i_{\max } \cdot V_{\max }}{2} \cos (\theta) = \left(\dfrac{i_{\max }}{\sqrt{2}}\right)\left(\dfrac{V_{\max }}{\sqrt{2}}\right) \cos (\theta) \\ { } \\ &=\underbrace{i_{\text {eff}} \cdot V_{\text {eff}}}_{\begin{array}{c} \text{Apparent} \\ \text{Power} \end{array}} \cdot \underbrace{\cos (\theta)}_{\begin{array}{c} \text{Power} \\ \text{Factor} \end{array}} \quad\quad\quad\quad {\text {Average AC Power }} \end{array} \nonumber \] Así, la potencia de CA promedio transferida en un límite del sistema es el producto de la corriente efectiva, el voltaje efectivo, y\(\cos (\theta)\).

Un examen más detallado de la relación de potencia de CA promedio, Ec. \(\PageIndex{10}\), muestra que es producto de la potencia aparente y del factor de potencia. Debido a que la potencia aparente no es realmente una potencia, frecuentemente se le dan las unidades de voltios-amperios. (Si observa la placa de identificación en equipos eléctricos de servicio pesado, con frecuencia verá los valores reportados en\(\mathrm{kV} \cdot \mathrm{A}\), kilovoltios-amperios). El factor de potencia puede tener un valor entre\(0\)\(1\) y y depende del comportamiento de la carga, específicamente la impedancia de carga. Determinar el ángulo de fase y el factor de potencia para un sistema eléctrico específico es el tema de cursos en análisis de circuitos, por ejemplo ES203 — Sistemas eléctricos, que la mayoría de ustedes tomarán más adelante. Para sistemas con una carga puramente resistiva el factor de potencia es uno\([\theta=0\) y\(\cos (\theta)=1]\). En este texto, a menos que se le diga otra cosa, puede asumir que el factor de poder es la unidad. (Tenga en cuenta que esta suposición siempre le da la máxima potencia eléctrica posible para una situación determinada).

7.8.3 Almacenamiento de Energía Eléctrica

Cuando la energía es transferida hacia o desde un sistema por el flujo de corriente eléctrica, ¿qué sucede con esta energía dentro del sistema? La respuesta a esta pregunta depende de lo que hay dentro del sistema. En esta sección, nos limitaremos a los dispositivos que se encuentran comúnmente en los circuitos eléctricos: resistencias, capacitores, inductores y baterías.

Para nuestra discusión, asumiremos que nuestro sistema puede almacenar energía en seis formas diferentes:\[E_{\text {system}} = U + \underbrace{E_{MF}+E_{EF}}_{\text {Electrical Energy}} + \underbrace{E_{K, \text { trans}} + E_{K, \text { rot}} + E_{GP}}_{\text {Mechanical Energy}} \nonumber \]\[\begin{aligned} \text{where} \quad\quad\quad & \\ U &=\text { internal energy } \\ E_{EF} &=\text { energy stored in an electric field } \\ E_{MF} &=\text { energy stored in a magnetic field } \\ E_{K, \text { trans}} &=\text { translational kinetic energy } \\ E_{K, \text { rot}} &=\text { rotational kinetic energy } \\ E_{GP} &=\text { gravitational potential energy } \end{aligned} \nonumber \]

Los nuevos actores en esta discusión son la energía almacenada en un campo eléctrico y la energía almacenada en un campo magnético. Por escrito Eq. \(\PageIndex{11}\)con seis términos discretos de energía, hemos asumido que los términos energéticos son independientes entre sí. Esto será suficiente para nuestra discusión aquí; sin embargo, una presentación más detallada de la termodinámica revelaría que hay muchas situaciones en las que los términos eléctricos y energéticos internos no son independientes y deben ser tratados como un solo término (J. Kestin, A Course in Thermodinamia, Blaisdell Publishing Co, Waltham, Massachusetts, 1966, capítulo 8.).

Si nos limitamos a un sistema cerrado, entonces el balance energético se convierte\[\frac{d}{dt}\left[U + E_{K, \text { trans}} + E_{K, \text { rot}} + E_{GP} + E_{EF}+E_{MF}\right] = \dot{Q}_{\text {net}, \text { in }} + \dot{W}_{\text {net}, \text { in}} \nonumber \] Ahora consideremos varios componentes diferentes que a menudo se encuentran en un sistema eléctrico.

Resistor

Uno de los componentes más básicos de un circuito eléctrico es una resistencia. Para nuestros propósitos, asumiremos que una resistencia ideal es aquella que satisface la ley de Ohm\(V_{R}=i R\) como se ilustra en la Figura\(\PageIndex{2}\) y no puede almacenar energía en campos eléctricos y magnéticos.

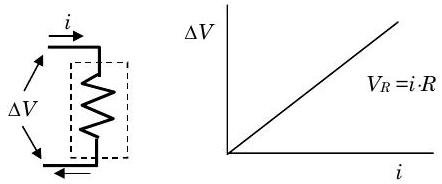
Figura\(\PageIndex{2}\): Relación voltaje-corriente para una resistencia ideal.

Si aplicamos la conservación de energía a una resistencia adiabática, ideal encontramos lo siguiente:\[\begin{aligned} \frac{d}{dt} E_{\text {resistor}} &= \dot{W}_{\text {net, in}} + \cancel{\dot{Q}_{\text {net, in}}}^{=0} \\ \frac{d}{dt} \left[U + \cancel{E_{K, \text { trans}}} + \cancel{E_{K, \text { rot}}} + \cancel{E_{\text {GP}}} + \cancel{E_{\text {MF}}} + \cancel{E_{EF}} \right] &= i \cdot \Delta V \quad \text { where } \Delta V=V_{R} \\ \frac{dU}{dt} &= i \cdot V_{R} = i \cdot(iR) \end{aligned} \nonumber \] Finalmente tenemos\[\frac{d E_{\text {resistor}}}{dt} = \frac{dU}{d }=i^{2} \cdot R \nonumber \] Así que la energía eléctrica suministrada a una resistencia adiabática, ideal resulta en un incremento en la energía interna del sistema. Por un periodo de tiempo finito, el cambio en la energía de la resistencia es\[\Delta E_{\text {resistor}}=\Delta U=\int\limits_{t_{1}}^{t_{2}}\left(i^{2} \cdot R\right) dt \quad \geq 0 \nonumber \] Tenga en cuenta que esta es una transferencia irreversible de energía porque cambiar la dirección de la corriente no disminuirá la energía interna del sistema.

Capacitor

El segundo componente básico del circuito que examinaremos es el condensador. Un condensador consta de dos superficies cargadas separadas por un dieléctrico. Para nuestros propósitos, un condensador ideal será aquel que solo pueda almacenar energía en un campo eléctrico dentro del condensador y que satisfaga la relación voltaje-corriente plasmada en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Relación voltaje-corriente para un condensador ideal.

El análisis de esta figura muestra que el voltaje a través del condensador y la corriente están relacionados por la expresión:\[i=C \frac{dV_{C}}{d t} \nonumber \] donde\(C\) está la capacitancia y se mide en faradios\((\mathrm{F})\) y\(1 \mathrm{~F} = (1 \mathrm{~A})(1 \mathrm{~s}) /(1 \mathrm{~V})\).

Aplicar la conservación de energía a un condensador adiabático ideal da lo siguiente:\[\begin{aligned} \frac{d}{dt} E_{\text {capacitor}} &= \dot{W}_{\text {net, in}} + \cancel{\dot{Q}_{\text {net, in}}}^{= 0} \\ \frac{d}{dt}\left[\cancel{U} + \cancel{E_{K, \text { trans}}} + \cancel{E_{K, \text { rot}}} + \cancel{E_{GP}} + E_{EF} + \cancel{E_{MF}} \right] &= i \cdot \Delta V \quad \text { where } \Delta V=V_{C} \\ \frac{d E_{EF}}{dt} &= i \cdot V_{C} = \left(C \frac{d V_{C}}{dt}\right) \cdot V_{C} \end{aligned} \nonumber \]

Por último tenemos\[\frac{d E_{\text {capacitor}}}{dt}=\frac{d E_{E F}}{d t}=\frac{d}{d t}\left(C \frac{V_{C}{ }^{2}}{2}\right) \quad \text { where } E_{\text {capacitor }} \equiv C \frac{V_{C}{ }^{2}}{2} \nonumber \] Así que la energía eléctrica instantánea suministrada a un condensador adiabático, ideal da como resultado un cambio en la energía almacenada en el campo eléctrico dentro del condensador. Si el condensador está sometido a una tensión de CA, la energía promediada en el tiempo almacenada en el condensador se calcula sustituyendo la tensión efectiva de la siguiente manera. \[\left.E_{\text {capacitor}}\right|_{\text {average AC }} = C \frac{V_{C, \text { eff}}{ }^{2}}{2} \quad\quad \begin{gathered} \text { Average energy stored } \\ \text { in a capacitor driven by } \\ \text { an AC voltage. } \end{gathered} \nonumber \]Por un periodo de tiempo finito, el cambio en la energía del condensador es solo el cambio en la energía del condensador:\[\Delta E_{\text {capacitor}} = \Delta E_{EF} = \frac{C}{2}\left(V_{C, 2}{ }^{2}-V_{C, 1}{ }^{2}\right) \nonumber \] Observe que a diferencia del almacenamiento de energía en la resistencia, la energía almacenada en un condensador adiabático puede aumentar y disminuir.

Inductor

El tercer componente básico del circuito que examinaremos es el inductor. Un inductor consiste en bobina cilíndrica de alambre. Para nuestros propósitos, un inductor ideal será aquel que solo pueda almacenar energía en un campo magnético dentro del inductor y que satisfaga la relación voltaje-corriente plasmada en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Relación voltaje-corriente para un inductor ideal.

El análisis de esta figura muestra que el voltaje a través del inductor y la corriente están relacionados por la expresión:\[V_{L}=L \frac{di}{dt} \nonumber \] donde\(L\) está la inductancia y se mide en henrys\((\mathrm{H})\) y\(1 \mathrm{H} = (1 \mathrm{~V})(1 \mathrm{~s}) / (1 \mathrm{~A})\).

Aplicar la conservación de energía a un inductor adiabático ideal da los siguientes resultados:\[\begin{aligned} \frac{d}{dt} E_{\text {inductor}} &= \dot{W}_{\text {net, in}} + \cancel{\dot{Q}_{\text {net, in}}}^{= 0} \\ \frac{d}{dt}\left[\cancel{U} + \cancel{E_{\text {K, trans}}} + \cancel{E_{K, \text { rot}}} + \cancel{E_{GP}} + \cancel{E_{EF}} + E_{MF}\right] &= i \cdot \Delta V \quad \text { where } \Delta V=V_{L} \\ \frac{d E_{MF}}{dt} &= i \cdot V_{L} = i \cdot\left(L \frac{di}{dt}\right) \end{aligned} \nonumber \]

Por último tenemos\[\frac{d E_{\text {Inductor}}}{dt} = \frac{d E_{MF}}{dt} = \frac{d}{dt}\left(L \frac{i^{2}}{2}\right) \quad \text { where } \quad E_{\text {Inductor}} \equiv L \frac{i^{2}}{2} \nonumber \] Así que la energía eléctrica suministrada a un inductor adiabático, ideal da como resultado un cambio en la energía almacenada en el campo magnético dentro del inductor. Si el inductor se somete a una corriente de CA, la energía promediada en el tiempo almacenada en la energía se calcula sustituyendo la corriente efectiva de la siguiente manera:\[\left.E_{\text {inductor}}\right|_{AC} = L \frac{i_{\text {eff}}{ }^{2}}{2} \quad\quad \begin{gathered} \text { Average energy stored } \\ \text { in an inductor driven } \\ \text { by an AC current } \end{gathered} \nonumber \] Por un período de tiempo finito, el cambio en la energía del inductor es solo el cambio en la energía del inductor:\[\Delta E_{\text {inductor}} = \Delta E_{MF} = \frac{L}{2}\left(i_{2}{ }^{2} - i_{1}{ }^{2}\right) \nonumber \] Observe que a diferencia de la energía almacenada en la resistencia, la energía almacenada en el inductor adiabático puede aumentar y disminuir.

Batería

El último componente que consideraremos es la batería. Una batería ideal satisfará la relación voltaje-corriente que se muestra en la Figura\(\PageIndex{5}\) y no puede almacenar energía en campos eléctricos y magnéticos.

Figura\(\PageIndex{5}\): Relación voltaje-corriente para una batería ideal.

Si aplicamos conservación de energía a la batería adiabática, ideal tenemos el resultado de que\[\begin{aligned} \frac{d E_{\text {battery}}}{dt} &=\dot{W}_{\text {net, in}} + \cancel{ \dot{Q}_{\text {net, in}} }^{=0} \\ \frac{d}{dt}\left[U + \cancel{E_{K, \text { trans}}} + \cancel{E_{K, \text { rot}}} + \cancel{E_{GP}} + \cancel{E_{UF}} + \cancel{E_{EF}}\right] &= i \cdot \Delta V \quad\quad \text { where } \Delta V=\Delta V_{\text {cell}} \\ \frac{dU}{dt} &= i \cdot \Delta V_{\text {cell}} \end{aligned} \nonumber \] así finalmente, tenemos para la batería adiabática, ideal,\[\frac{d E_{\text {battery}}}{dt} = \frac{dU}{dt} = i \cdot \Delta V_{\text {cell}} \nonumber \] así la energía eléctrica suministrada a una batería entra en un cambio en la energía interna de la batería.

Para un intervalo de tiempo finito, el cambio en la energía de la batería se escribe de la siguiente manera:\[\Delta E_{\text {battery}} = \Delta U = \int\limits_{t_{1}}^{t_{2}} \left(i \cdot \Delta V_{\text {cell}}\right) d t \nonumber \]

Tenga en cuenta que al igual que tanto el condensador como el inductor y a diferencia de la resistencia, la energía interna de una batería adiabática ideal puede aumentar y disminuir.

7.8.4 Alimentación de CA y sistemas de estado estacionario

Cuando un sistema recibe alimentación de CA, la potencia instantánea y, por lo tanto, la tasa de transferencia de energía en el límite cambia con el tiempo de manera periódica. Nuestra suposición de estado estacionario requiere que nada dentro o en los límites del sistema cambie con el tiempo. Esto parecería impedirnos asumir un comportamiento de estado estacionario cuando se suministra energía de CA a un sistema. Sin embargo, nuestro mundo está lleno de sistemas impulsados por energía de CA que, a pesar de todo, parecerían estar operando en condiciones de “estado estacionario”.

Para manejar este aparente conflicto, podemos aprovechar nuestra experiencia con la energía eléctrica promedio que desarrollamos anteriormente en la Sección 7.8.1. Si promediamos el tiempo-forma de la ecuación de conservación de energía como lo hicimos al encontrar la potencia eléctrica promedio, terminamos con una ecuación que se parece exactamente a la forma de tasa original de la ecuación de conservación de energía. La única diferencia es que cada término ha sido promediado en el tiempo. Si solo nos interesa el comportamiento del sistema en escalas de tiempo mucho mayores que 1 periodo de una señal AC (\(1 / 60 \mathrm{~s}\)) la ecuación promediada en el tiempo funcionará igual que la ecuación original.

Ahora cuando decimos que un sistema con alimentación de CA está operando en condiciones de estado estacionario, lo que realmente estamos diciendo es que en promedio el sistema no está cambiando con el tiempo. Esto significa que la potencia de CA promedio no cambia con el tiempo. También significa que cualquier otra cosa sobre el sistema que variaba periódicamente con el tiempo, por ejemplo, el almacenamiento de energía en condensadores e inductores, no cambia en promedio con el tiempo.

Este fenómeno no es realmente exclusivo de la energía eléctrica. Si monitorea el par del eje de transmisión que sale del motor de su automóvil, probablemente descubrirá que aunque la velocidad de rotación del eje es constante, el par variará con el ángulo del eje a medida que gira el eje. Esto da un par de eje que varía periódicamente con el tiempo. Por lo tanto, la potencia del eje puede realmente fluctuar, pero solo reportamos un valor promedio. Entonces, sin siquiera saberlo, a veces estamos invocando los supuestos de estado estacionario “promediados en el tiempo”. Claramente, si necesitábamos analizar el comportamiento del sistema en una escala de tiempo igual al período de una rotación del eje, sería incorrecto promediar las fluctuaciones