7.8: Resolver programación dinámica en una computadora

Última actualización
Guardar como PDF

Page ID: 84129

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ciertamente, el algoritmo anterior puede implementarse como escrito, moviéndose hacia atrás desde el final hasta el principio, manteniendo un seguimiento en cada etapa solo de las trayectorias óptimas de esa etapa en adelante. Esta decisión implicará una cuidadosa grabación e indexación. Un algoritmo muy simple llamado iteración de valor puede ser más accesible en su primer intento. Como mostraremos en un ejemplo a continuación, la iteración de valores también nos permite considerar problemas donde distintas etapas no están claras.

Va de esta manera:

Indizar todas las configuraciones posibles, o nodos, del sistema (ciudades).
Con cada configuración, crear una lista de donde podemos ir desde ese nodo - probablemente esta es una lista de índices (ciudades que son plausiblemente parte de una ruta óptima). El nodo inicial (Los Ángeles) no es apuntado por ningún otro nodo, mientras que el nodo final (Boston) apunta a ninguno.
Para cada una de estas rutas simples definidas de nodo a nodo, asigne un costo de transición (simples millas de conducción entre las ciudades).
Ahora asigne a cada una de estas configuraciones una suposición inicial para el costo desde este nodo hasta el estado final (óptimo total de millas desde cada ciudad hasta Boston). Claramente los costos por llevar para los nodos que apuntan al nodo terminal son bien conocidos, pero ninguno de los otros lo es.
Recorre todas las configuraciones (excepto la terminal), escogiendo la mejor ruta de salida, en función de la ruta local y el costo estimado en el siguiente nodo. En cada nodo, solo tenemos que hacer un seguimiento del mejor índice de nodo siguiente, y el nuevo costo estimado para llevar.
¡Repite a la convergencia!

Se puede demostrar que este algoritmo siempre converge, y tiene una serie de variantes y mejoras. Un ejemplo aclara las cosas:

Nodo	Puntos a Nodos	Con Costos	Estimación Inicial del Costo a Ir
\(A\)(inicial)	\(B, C, D\)	\(4, 2, 6\)	\(10\)
\(B\)	\(C, D, E\)	\(3, 2, 5\)	\(10\)
\(C\)	\(D, E\)	\(6, 5\)	\(10\)
\(D\)	\(E\)	\(2\)	\(2\)(conocido)
\(E\)	(terminal)	N/A	N/A

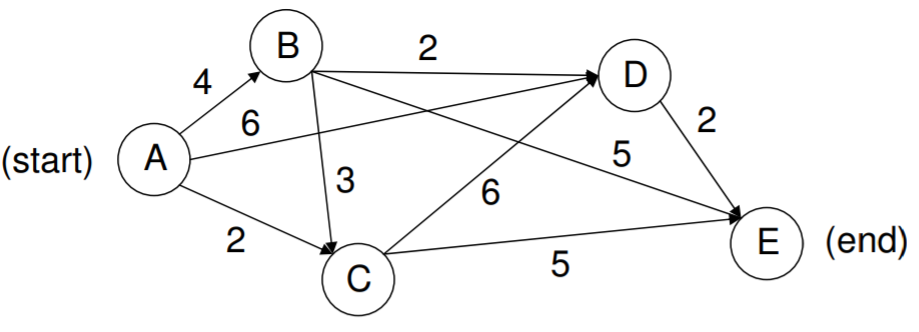Visualización de un problema de ruta más corta con 3 nodos ubicados a distancias variables entre un punto inicial y un punto final. Los costos de desplazamiento entre dos nodos cualesquiera (las millas cubiertas) están marcados en las flechas correspondientes. — Figura\(\PageIndex{1}\): se muestran las ubicaciones de las cinco ciudades (nodos), junto con el costo de viajar de cualquiera de las ciudades a cualquier otra en la dirección que se aproxime al destino\(E\).

Y aquí está la evolución de la iteración del valor:

Iteración	\(A\)costo-a-go	\(B\)costo-a-go	\(C\)costo-a-go	\(D\)costo-a-go
\(0\)	\ (A\) Costo-a-Go">N/A	\ (B\) costo de salir">\(10\)	\ (C\) costo de salir">\(10\)	\ (D\) costo-para-salir">\(2(E)\)
\(1\)	\ (A\) costo para ir">\(\min (14, 12, 8) = 8(D, E)\)	\ (B\) costo de salir">\(\min (13, 4, 5) = 4(D, E)\)	\ (C\) costo de salir">\(\min (8, 5) = 5(E)\)	\ (D\) costo-para-salir">\(2(E)\)
\(2\)	\ (A\) costo para ir">\(\min (8, 7, 8) = 7(C, E)\)	\ (B\) costo de salir">\(4(D, E)\)	\ (C\) costo de salir">\(5(E)\)	\ (D\) costo-para-salir">\(2(E)\)

Podemos terminar de manera segura después de la segunda iteración porque la ruta de\(A\) implica\(C\), que no puede cambiar de su valor después de la primera iteración, porque se conecta todo el camino a través de\(E\).