7.5: Desviación por Método Momento-Área

El método momento-área utiliza el área de momento dividida por el diagrama de rigidez a la flexión (\(M / E D\)) de una viga para determinar la deflexión y pendiente a lo largo de la viga. Hay dos teoremas utilizados en este método, los cuales se derivan a continuación.

Teorema del Primer Momente-Área

Para derivar el teorema del primer momente-área, considere una porción\(AB\) de una curva elástica de la viga desviada que se muestra en la Figura 7.8b. La viga tiene un radio de curvatura\(R\). La Figura 7.8c representa el momento de flexión de esta porción. De acuerdo con la geometría, la longitud del arco\(ds\), del radio\(R\), subtendiendo un ángulo\(d \theta\), es igual al producto del radio de curvatura y el ángulo subtiende. Por lo tanto,

\[d s=R d \theta\]

Reorganizar la ecuación 1 sugiere lo siguiente:

\[\frac{d \theta}{d s}=\frac{1}{R}\]

\(Fig. 7.8\). Viga desviada.

Sustituir la ecuación 7.14 por la ecuación 7.8 sugiere lo siguiente:

\[d \theta=\frac{M}{E I} d s\]

Dado que\(ds\) es infinitesimal por la pequeña desviación lateral de la viga que se permite en la ingeniería, puede ser reemplazada por su proyección horizontal\(dx\). Por lo tanto,

\[d \theta=\frac{M}{E I} d x\]

El ángulo\(\theta\) entre las tangentes en\(A\) y se\(B\) puede obtener así resumiendo los ángulos subtendidos por la longitud infinitesimal que se encuentra entre estos puntos. Por lo tanto,

\ [\ begin {array} {l}
\ int_ {A} ^ {B} d\ theta=\ int_ {A} ^ {B}\ frac {M} {E I} d x\\
\ nombredeoperador {O}\ theta_ {B/A} =\ theta_ {B} -\ theta_ {A} =\ int_ {A} ^ B}\ frac {M} {E I} d x
\ end {array}\]

La ecuación 7.17 es referida como el primer teorema de momente-área. El teorema del primer momente-área establece que el cambio total de pendiente entre\(A\) y\(B\) es igual al área del diagrama de momento de flexión entre estos dos puntos dividido por la rigidez a la flexión\(EI\).

Teorema del Segundo Momente-Área

Refiriéndose nuevamente a la Figura 7.8, se requiere determinar la desviación tangencial del punto\(B\) con respecto al punto\(A\), que es la distancia vertical del punto\(B\) desde la tangente dibujada a la curva elástica en el punto\(A\). Para ello, primero calcule la contribución\(\delta \Delta\) del elemento de longitud\(dL\) a la distancia vertical. Según la geometría,

\[\delta y=x d \theta\]

Sustituir\(d \theta\) de la ecuación 7.15 a la ecuación 7.18 sugiere lo siguiente:

\[\delta y=\frac{M x}{E I} d x\]

Por lo tanto,

\[y=\int_{A}^{B} \frac{M x}{E I} d x\]

La ecuación 7.20 se conoce como el teorema del área del segundo momento. El segundo teorema momento-área establece que la distancia vertical del punto\(B\) en una curva elástica desde la tangente a la curva en el punto\(A\) es igual al momento con respecto al paso vertical\(B\) del área del diagrama de momento de flexión entre\(A\) y\(B\), dividido por la rigidez a la flexión,\(EI\).

Convenciones de Firmar

Las convenciones de signos para teoremas de área de momento son las siguientes:

(1) La desviación tangencial de un punto\(B\), con respecto a una tangente dibujada en la curva elástica en un punto\(A\), es positiva si se\(B\) encuentra por encima de la tangente dibujada en\(A\) y negativa si se encuentra por debajo de la tangente (ver Figura 7.9).

(2) La pendiente en un punto\(B\), con respecto a una tangente dibujada\(A\) en un punto de una curva elástica, es positiva si la tangente dibujada en\(B\) gira en sentido contrario a las agujas del reloj con respecto a la tangente en\(A\) y negativa si gira en sentido horario (ver Figura 7.9).

\(Fig. 7.9\). Firmar representación convención.

Procedimiento de Análisis por Método Momento-Área

•Dibuje el diagrama de cuerpo libre de la viga.

•Dibuja el\(M/EI\) diagrama de la viga. Esto se verá como el diagrama de momento de flexión convencional de la viga si la viga es prismática (es decir, de la misma sección transversal para toda su longitud).

•Para determinar la pendiente en cualquier punto, busque el ángulo entre una tangente que pasa por el punto y una tangente que pasa por otro punto de la curva desviada, divida el\(M/EI\) diagrama en formas geométricas simples y luego aplique el primer teorema de momente-área. Para determinar la deflexión o desviación tangencial de cualquier punto a lo largo de la viga, aplique el segundo teorema momente-área.

•En los casos en que la configuración del\(M/EI\) diagrama sea tal que no pueda dividirse en formas simples con áreas y centroides conocidos, es preferible dibujar el\(M/EI\) diagrama por partes. Esto implica introducir un soporte fijo en cualquier punto conveniente a lo largo de la viga y dibujar el\(M/EI\) diagrama para cada una de las cargas aplicadas, incluyendo las reacciones de soporte, previo a la aplicación de cualquiera de los teoremas para determinar lo que se requiere.

Cuadro 7.1. Áreas y centroides de formas geométricas.

Forma Geométrica		Área	Centroide
			C 1	C 2
Rectángulo		\(bh\)	\(\frac{b}{2}\)	\(\frac{b}{2}\)
Triángulo		\(\frac{bh}{2}\)	\(\frac{b}{3}\)	\(\frac{2b}{3}\)
Spandrel parabólico		\(\frac{bh}{3}\)	\(\frac{b}{4}\)	\(\frac{3b}{4}\)
		\(\frac{2bh}{3}\)	\(\frac{3b}{8}\)	\(\frac{5b}{8}\)
Spandrel cúbico		\(\frac{bh}{4}\)	\(\frac{b}{5}\)	\(\frac{4b}{5}\)
		\(\frac{3bh}{4}\)	\(\frac{2b}{5}\)	\(\frac{3b}{5}\)
General Spandrel		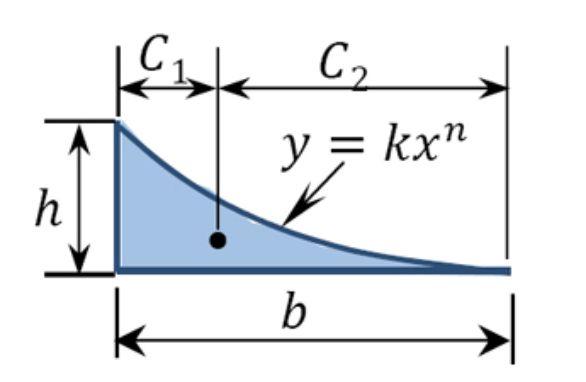\(\frac{bh}{n+1}\)	\(\frac{b}{n+2}\)	\(\frac{b(n+1)}{n+2}\)

Ejemplo 7.7

Una viga en voladizo mostrada en la Figura 7.10a se somete a un momento concentrado en su extremo libre. Mediante el método de área temporal, determine la pendiente en el extremo libre de la viga y la deflexión en el extremo libre de la viga. \(EI\)= constante.

\(Fig. 7.10\). Viga en voladizo.

Solución

(\(M/EI\)) diagram.Primero, dibuje el diagrama del momento de flexión para la viga y divídalo por la rigidez a la flexión\(EI\),, para obtener el\(\frac{M}{E I}\) diagrama mostrado en la Figura 7.10b.

Pendiente en\(A\). La pendiente en el extremo libre es igual al área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(B\), según el teorema del primer momente-área. Usando este teorema y haciendo referencia al\(\frac{M}{E I}\) diagrama sugiere lo siguiente:

\(\theta_{A}=-\left(\frac{1}{E I}\right)(6)(20)=-\frac{120}{E I}\)

Deflexión en\(A\). La deflexión en el extremo libre de la viga es igual al momento con respecto al paso vertical\(A\) del área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(B\), de acuerdo con el teorema del segundo momente-área. Usando este teorema y haciendo referencia a la Figura 7.10b y Figura 7.10c sugiere lo siguiente:

\(\Delta_{A}=-\left(\frac{1}{E I}\right)(6)(20)(3)=-\frac{360}{E I} \quad \Delta_{A}=\frac{360}{E I} \downarrow\)

Ejemplo 7.8

Una viga en voladizo apoyada lleva una carga uniformemente distribuida de 4 kips/ft en toda su longitud, como se muestra en la Figura 7.11a. Usando el método de momente-área, determinar la pendiente en\(A\) y la deflexión en\(A\).

\(Fig. 7.11\). Viga en voladizo apoyada.

Solución

(\(M/EI\)) diagram.Primero, dibuje el diagrama del momento de flexión para la viga y divídalo por la rigidez a la flexión\(EI\),, para obtener el\(\frac{M}{E I}\) diagrama mostrado en la Figura 7.11b.

Pendiente en\(A\). La pendiente en el extremo libre es igual al área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(B\). El área entre estos dos puntos se indica como\(A_{1}\) y\(A_{2}\) en la Figura 7.11b. Utilice la Tabla 7.1 para encontrar el cálculo de\(A_{2}\), cuyo arco es parabólico, y la ubicación de su centroide. Observando de la tabla que\(A=\frac{1}{3} b h\) y aplicando el teorema del primer momente-área sugiere lo siguiente:

\(\theta_{A}=A_{1}-A_{2}=\left(\frac{1}{E I}\right)\left(\frac{1}{2}\right)(10)(120)-\left(\frac{1}{E I}\right)\left(\frac{10 \times 200}{3}\right)=-\frac{66.67}{E I}\)

Deflexión en\(A\). La deflexión en\(A\) es igual al momento del área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(B\) aproximadamente\(A\). Así, utilizando el teorema del segundo momente-área y haciendo referencia a la Figura 7.11b y Figura 7.11c sugiere lo siguiente:

\(\Delta_{A}=A_{1}\left(\frac{L}{3}\right)-A_{2}\left(\frac{3 L}{4}\right)=\left(\frac{1}{E I}\right)\left(\frac{1}{2}\right)(10)(120)\left(\frac{2 \times 10}{3}\right)-\left(\frac{1}{E I}\right)\left(\frac{10 \times 200}{3}\right)\left(\frac{3 \times 10}{4}\right)=-\frac{1000}{E I} \quad \Delta_{A}=\frac{1000}{E I} \downarrow\)

Ejemplo 7.9

Una viga de madera simplemente soportada con una longitud de 8 pies llevará una carga de piso distribuida de 500 lb/ft en toda su longitud, como se muestra en la Figura 7.12a. Utilizando el teorema del área del momento, determinar la pendiente al final\(B\) y la deflexión máxima.

\(Fig. 7.12\). Viga de madera simplemente soportada.

Solución

(\(M/EI\)) diagram.Primero, dibuje el diagrama del momento de flexión para la viga, y divídalo por la rigidez a la flexión,\(EI\), para obtener el\(\frac{M}{E I}\) diagrama que se muestra en la Figura 7.12b.

Pendiente en\(B\). La pendiente en\(B\) es igual al área del\(\frac{M}{E I}\) diagrama entre\(B\) y\(C\). El área entre estos dos puntos se indica como\(A_{2}\) en la Figura 7.12b. La aplicación del teorema del primer momente-área sugiere lo siguiente:

\(\theta_{B}=A_{2}=\left(\frac{1}{E I}\right)\left(\frac{2 b h}{3}\right)=\left(\frac{1}{E I}\right)\left(\frac{2(4)(4000)}{3}\right)=\frac{10666.67}{E I}\)

Deflexión máxima. La desviación máxima se produce en el centro de la viga (punto C). Es igual al momento del área del\(\frac{M}{E I}\) diagrama entre\(B\) y\(C\) aproximadamente\(B\). Por lo tanto,

\(\Delta_{c}=A_{2}\left(\frac{5 b}{8}\right)=\left(\frac{1}{E I}\right)\left(\frac{2(4)(4000)}{3}\right)\left(\frac{5(4)}{8}\right)=\frac{26666.67}{E I}\)

Ejemplo 7.10

Una viga prismática de madera se somete a dos cargas concentradas de igual magnitud, como se muestra en la Figura 7.13a. Usando el método de área temporal, determine la pendiente en\(A\) y la deflexión en el punto\(C\).

\(Fig. 7.13\). Viga prismática de madera.

Solución

(\(M/EI\)) diagram.Primero, dibuje el diagrama del momento de flexión para la viga y divídalo por la rigidez a la flexión\(EI\),, para obtener el\(\frac{M}{E I}\) diagrama mostrado en la Figura 7.13b.

Pendiente en\(A\). La deflexión y la rotación de la viga son pequeñas ya que ocurren dentro del límite elástico. Así, la pendiente en soporte se\(A\) puede calcular utilizando el teorema de ángulo pequeño, de la siguiente manera:

\(\theta_{A}=\frac{\Delta_{B / A}}{L}=\frac{\Delta_{B / A}}{6}\)

Para determinar la desviación tangencial de\(B\) de\(A\), aplicar el segundo teorema momente-área. Según el teorema, es igual al momento del área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(B\) aproximadamente\(B\). Por lo tanto,

\ (\ begin {array} {l}
\ Delta_ {B/A} =A_ {1}\ left (1.5+3+\ frac {1} {3}\ times 1.5\ right) +A_ {2} (1.5+1.5) +A_ {3}\ left (\ frac {2} {3}\ times 1.5\ right)\\
\ Delta_ {B/A} = frac {1} {E I}\ left [\ frac {1} {2} (1.5) (6)\ left (\ frac {2} {3}\ times 1.5\ right) + (3) (6) (1.5+1.5) +\ frac {1} {2} (1.5) (6)\ left (1.5+3+\ frac {1} {3}\ veces 1.5\ derecha)\ derecha]\\
\ Delta_ {B/A} =\ frac {81} {E I}
\ end {array}\)

Así, la pendiente en\(A\) es

\(\theta_{A}=\frac{\Delta_{B / A}}{L}=\frac{81}{6 E I}=\frac{13.5}{E I} \quad \theta_{A}=\frac{13.5}{E I}\)

Deflexión en\(C\). La deflexión en se\(C\) puede obtener por proporción.

\ (\ begin {array} {l}
\ frac {\ Delta_ {B/A}} {6} =\ frac {\ Delta_ {c} +\ Delta_ {C/A}} {1.5}\
\ Delta_ {c} =\ frac {(1.5)\ left (\ Delta_ {B/A}\ derecha)} {6} -\ Delta_ {C/A}
\ final {matriz}\)

De igual manera, la desviación tangencial de\(C\) desde se\(A\) puede determinar como el momento del área del\(\frac{M}{E I}\) diagrama entre\(A\) y\(C\) aproximadamente\(C\).

\(\Delta_{C / A}=\frac{1}{E I}\left[\frac{1}{2}(1.5)(6)\left(\frac{2}{3} \times 1.5\right)\right]=\frac{9}{2 E I}\)

Por lo tanto, la deflexión en\(C\) es

\(\Delta_{c}=\frac{(1.5)(81)}{6 E I}-\frac{9}{2 E I}=\frac{15.75}{E I} \quad \Delta_{c}=\frac{15.75}{E I}\)