7.6: Desviación por el Método de Haz Conjugado

El método de haz conjugado, desarrollado por Heinrich Muller-Breslau en 1865, es uno de los métodos utilizados para determinar la pendiente y deflexión de una viga. El método se basa en el principio de la estática.

Una viga conjugada se define como una viga ficticia cuya longitud es la misma que la de la viga real, pero con una carga igual al momento de flexión de la viga real dividida por su rigidez a la flexión,\(EI\).

El método de viga conjugada aprovecha la similitud de la relación entre carga, fuerza cortante y momento de flexión, así como entre curvatura, pendiente y deflexión derivada en capítulos anteriores y presentada en la Tabla 7.2.

\(Table 7.2\). Relación entre carga-cizalla-momento de flexión y curvatura-pendiente-deflexión.

Soportes para Vigas Conjugadas

Los soportes para haces conjugados se muestran en la Tabla 7.3 y los ejemplos de haces reales y conjugados se muestran en la Figura 7.4.

\(Table 7.3\). Soportes para haces conjugados.

\(Table 7.4\)Vigas reales y su conjugado.

Convención de Firmar

Para un diagrama de curvatura positiva, donde hay una ordenada positiva del\(\frac{M}{E I}\) diagrama, la carga en el conjugado debe apuntar en la\(y\) dirección positiva (hacia arriba) y viceversa (ver Figura 7.14).

\(Fig. 7.14\). Diagrama de curvatura positiva.

Si se sigue la convención establecida para los diagramas de curvatura positiva, entonces una fuerza de cizallamiento positiva en el haz conjugado es igual a la pendiente positiva en el haz real, y un momento positivo en el haz conjugado equivale a una deflexión positiva (movimiento hacia arriba) del haz real. Esto se muestra en la Figura 7.15.

\(Fig. 7.15\). Cizalla y pendiente en viga.

Procedimiento de Análisis por Método de Haz Conjugado

•Dibuja el diagrama de curvatura para el haz real.

•Dibuja el haz conjugado para el haz real. El haz conjugado tiene la misma longitud que el haz real. Una rotación en cualquier punto del haz real corresponde a una fuerza de cizallamiento en el mismo punto en el haz conjugado, y un desplazamiento en cualquier punto del haz real corresponde a un momento en el haz conjugado.

•Aplicar el diagrama de curvatura de la viga real como carga distribuida sobre la viga conjugada.

•Usando las ecuaciones de equilibrio estático, determinar las reacciones en los soportes del haz conjugado.

•Determinar la fuerza cortante y el momento en las secciones de interés en la viga conjugada. Estas fuerzas cortantes y momentos son iguales a la pendiente y deflexión, respectivamente, en la viga real. El cizallamiento positivo en el haz conjugado implica una pendiente en sentido contrario a las agujas del reloj en el haz real, mientras que un momento positivo denota una desviación hacia arriba en el haz real.

Ejemplo 7.11

Utilizando el método de viga conjugada, determinar la pendiente y la deflexión en el punto\(A\) de la viga en voladizo que se muestra en la Figura 7.16a. \(E = 29,000 \mathrm{ksi}\)y\(I = 280 \mathrm{in.}^{4}\)

\(Fig. 7.16\). Haz conjugado.

Solución

(\(M/EI\)) diagram.Primero, dibuje el diagrama del momento de flexión para la viga y divídalo por la rigidez a la flexión\(EI\),, para obtener el\(\frac{M}{E I}\) diagrama mostrado en la Figura 7.16b.

Haz conjugado. El haz conjugado cargado con el\(\frac{M}{E I}\) diagrama se muestra en la Figura 7.16c. Observe que el extremo libre en el haz real se fija en el haz conjugado, mientras que el extremo fijo en el haz real se vuelve libre en el haz conjugado. El\(\frac{M}{E I}\) diagrama se aplica como una carga descendente en el haz conjugado porque es negativo en la Figura 7.16b.

Pendiente en\(A\). La pendiente\(A\) en la viga real es la cizalla\(A\) en la viga conjugada. El cizallamiento\(A\) en el conjugado es como sigue:

\(V_{A}=\left(\frac{1}{2}\right)(12)\left(\frac{36}{E I}\right)=\frac{216 \mathrm{k}-\mathrm{ft}^{2}}{E I}\)

Aquí se utiliza la misma convención de signos para la fuerza de corte utilizada en el Capítulo 4.

Así, la pendiente en la viga real en el punto\(A\) es la siguiente:

\(\theta_{\mathrm{A}}=\frac{216 \mathrm{k}-\mathrm{ft}^{2}}{E I}=\frac{216(12)^{2}}{(29,000)(280)}=0.0038 \mathrm{rad}\)

Deflexión en\(A\). La deflexión\(A\) en el haz real es igual al momento en\(A\) del haz conjugado. El momento en\(A\) el haz conjugado es el siguiente:

\(M_{A}=-\left(\frac{1}{2}\right)(12)\left(\frac{36}{E I}\right)\left(\frac{2}{3} \times 12\right)=-\frac{1728 \mathrm{k}-\mathrm{ft}^{3}}{E I}\)

Aquí se utiliza la misma convención de signos para el momento de flexión utilizada en el Capítulo 4.

Así, la deflexión en el haz real en el punto\(A\) es la siguiente:

\(\Delta_{\mathrm{A}}=-\frac{1728(12)^{3}}{(29,000)(280)}=-0.37 \mathrm{in} \quad \Delta_{A}-0.37 \mathrm{in} \downarrow\)

Ejemplo 7.12

Utilizando el método de haz conjugado, determinar la pendiente en el soporte\(A\) y la deflexión bajo la carga concentrada de la viga simplemente soportada en la figura 7.17a.\(B\)

\(E = 29,000 \mathrm{ksi}\)y\(I = 800 \mathrm{in.}^{4}\)

\(Fig. 7.17\). Viga simplemente soportada.

Solución

(\(M/EI\)) diagram. Primero, dibuje el diagrama de momento de flexión para la viga y divídalo por la rigidez a la flexión\(EI\),, para obtener el diagrama de curvatura de momento (\(\frac{M}{E I}\)) mostrado en la Figura 7.17b.

Haz conjugado. El haz conjugado cargado con el\(\frac{M}{E I}\) diagrama se muestra en la Figura 7.17c. Observe que\(A\) y\(C\), que son soportes simples en el haz real, siguen siendo los mismos en el haz conjugado. El\(\frac{M}{E I}\) diagrama se aplica como una carga ascendente en el haz conjugado porque es positivo en la Figura 7.17b.

Reacciones para haz conjugado. La reacción en los soportes del haz conjugado se puede determinar de la siguiente manera:

\(A_{y}=B_{y}=-\frac{1}{E I}\left(\frac{1}{2}\right)(30)(180)(0.5)=-\frac{1350 \mathrm{k} . \mathrm{ft}^{2}}{E I} \text { due to symmetry in loading }\)

Pendiente en\(A\). La pendiente\(A\) en la viga real es la fuerza de cizallamiento\(A\) en la viga conjugada. El cizallamiento\(A\) en el haz conjugado es como sigue:

\(V_{A}=-\frac{1350 \mathrm{k} \cdot \mathrm{ft}^{2}}{E I}\)

Así, la pendiente en soporte\(A\) de la viga real es la siguiente:

\(\theta_{A}=-\frac{1350 \mathrm{k} \cdot \mathrm{ft}^{2}}{E I}=-\frac{1350(12)^{2}}{(29,000)(800)}=-0.0084 \mathrm{rad}\)

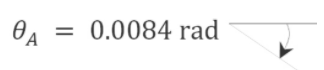
Deflexión en\(B\). La deflexión\(B\) en el haz real es igual al momento en\(B\) del haz conjugado. El momento en\(B\) el haz conjugado es el siguiente:

\(M_{B}=\frac{1}{E I}\left[-(1350)(15)+\left(\frac{1}{2}\right)(15)(180)\left(\frac{15}{3}\right)\right]=-\frac{13500 \mathrm{k} \cdot \mathrm{ft}^{3}}{E I}\)

La desviación en\(B\) de la viga real es la siguiente:

\(\Delta_{B}=-\frac{33750 \mathrm{k} \cdot \mathrm{ft}^{3}}{E I}=-\frac{13500(12)^{3}}{(29,000)(800)}=-1.01 \text { in. } \quad \Delta_{B}=1.01 \text { in. } \downarrow\)

Resumen del Capítulo

Desviación de vigas a través de métodos geométricos: Los métodos geométricos considerados en este capítulo incluyen el método de integración doble, el método de función de singularidad, el método de área de momento y el método de haz conjugado. Previo a la discusión de estos métodos, se derivó la siguiente ecuación de la curva elástica de una viga:

Método de doble integración: Este método implica integrar la ecuación de curva elástica dos veces. La primera integración produce la pendiente, y la segunda integración da la deflexión. Las constantes de integración se determinan considerando las condiciones de contorno.

Método de función de singularidad: Este método implica el uso de una función de singularidad o de medio rango para describir la ecuación de la curva elástica para toda la viga. Una función de rango medio se puede escribir en la forma general de la siguiente manera:

\ (\ langle x-a\ rangle^ {n} =\ left\ {\ begin {array} {c}
0\ text {for} (x-a) <0\ text {o} x<a\\
(x-a) ^ {n}\ text {for} x-a\ geq 0\ text {o} x\ geq a
\ end {array}\ right.\)

El método de singularidad es el más adecuado para vigas con muchas discontinuidades debido a cargas y momentos concentrados. El método reduce significativamente el número de constantes de integración que deben determinarse y, por lo tanto, facilita el cálculo en comparación con el método de doble integración.

Método Moment-area: Este método utiliza dos teoremas para determinar la pendiente y la deflexión en puntos especificados en la curva elástica de una viga. Los dos teoremas son los siguientes:

Teorema del primer momente-área: El cambio de pendiente entre dos puntos cualesquiera en la curva elástica de una viga es igual al área del\(\frac{M}{E I}\) diagrama entre estos dos puntos.

Teorema del segundo momento-área: La deflexión vertical del punto\(A\) desde la tangente dibujada a la curva elástica en el punto\(B\) es igual al momento del área debajo del\(\frac{M}{E I}\) diagrama entre estos dos puntos alrededor del punto\(A\).

Método de haz conjugado: Un haz conjugado se ha definido como un haz imaginario con la misma longitud que la del haz real pero con una carga igual al\(\frac{M}{E I}\) diagrama del haz real. Los soportes en las vigas reales son reemplazados por soportes ficticios con condiciones límite que darán como resultado el momento de flexión y la fuerza de corte en un punto específico en una viga conjugada igualando la deflexión y pendiente, respectivamente, en los mismos puntos de la viga real.

Problemas de práctica

7.1 Mediante el método de doble integración, se determinan las pendientes y deflexiones en los extremos libres de las vigas en voladizo mostradas en la Figura P7.1 a la Figura P7.4. \(EI\)= constante.

\(Fig. P7.1\). Viga en voladizo.

\(Fig. P7.2\). Viga en voladizo.

\(Fig. P7.3\). Viga en voladizo.

\(Fig. P7.4\). Viga en voladizo.

7.2 Mediante el método de doble integración, se determinan las pendientes en el punto\(A\) y las deflexiones en el punto medio\(C\) de las vigas mostradas en la Figura P7.5 y la Figura P7.6. \(EI\)= constante.

\(Fig. P7.5\). Viga.

\(Fig. P7.6\). Viga.

7.3 Utilizando el método de haz conjugado, determinar la pendiente en el punto\(A\) y la deflexión en el punto\(B\) de la viga mostrada en la Figura P7.7 a la Figura P7.10.

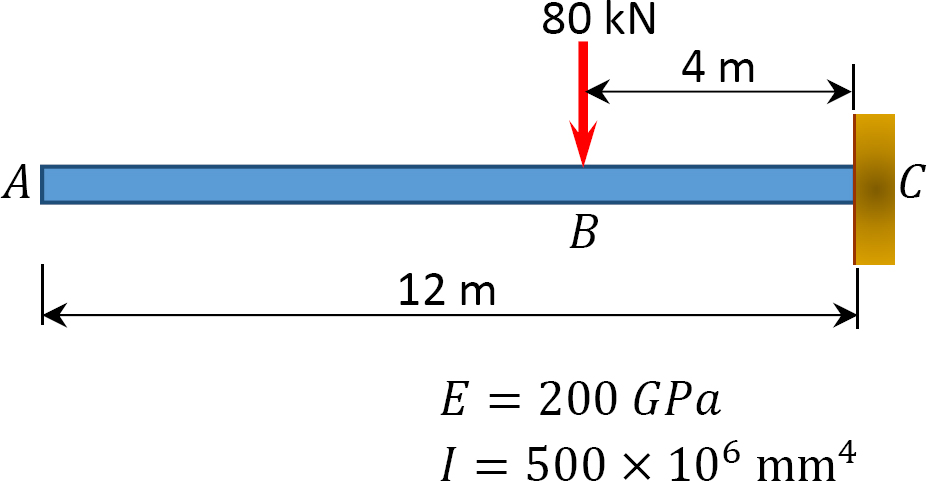
\(Fig. P7.7\). Viga.

\(Fig. P7.8\). Viga.

\(Fig. P7.9\). Viga.

\(Fig. P7.10\). Viga.

7.4 Utilizando el método momente-área, determinar la deflexión en el punto\(A\) de la viga en voladizo que se muestra en la Figura P7.11 a la Figura P7.12.

\(Fig. P7.11\). Viga en voladizo.

\(Fig. P7.12\). Viga en voladizo.

7.5 Mediante el método momente-área, se determina la pendiente en el punto\(A\) y la pendiente en el punto medio\(C\) de las vigas que se muestran en la Figura P7.13 y la Figura P7.14.

\(Fig. P7.13\). Viga.

\(Fig. P7.14\). Viga.

7.6 Utilizando el método de función de singularidad, determinar la pendiente y la deflexión en el punto\(A\) de la viga en voladizo que se muestra en la Figura P7.15.

\(Fig. P7.15\). Viga en voladizo.

7.7 Utilizando el método de función de singularidad, se determina la pendiente en el punto\(B\) y la pendiente en el punto\(C\) de la viga con el voladizo que se muestra en la Figura P7.16. \(EI\)= constante. \(E=200 \mathrm{GPa}, \mathrm{I}=500 \times 106 \mathrm{~mm}^{4}\).

\(Fig. P7.16\). Viga.

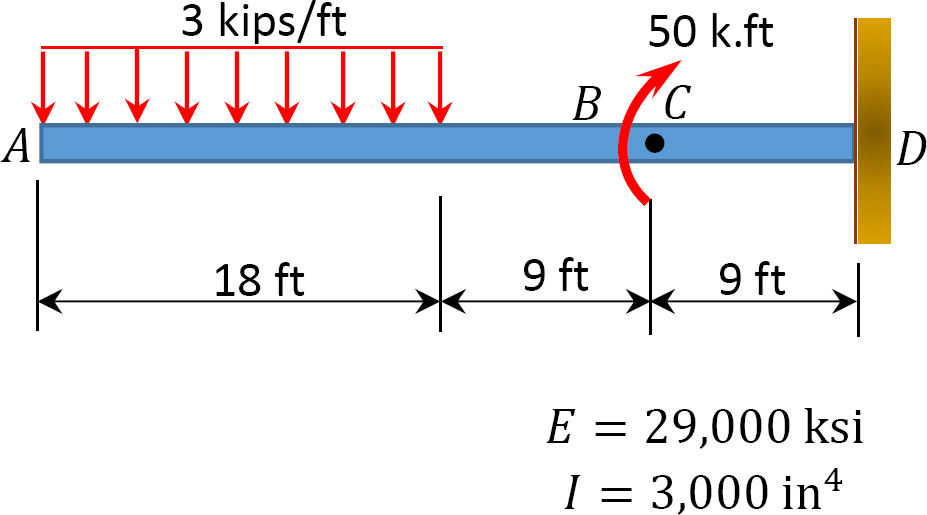
7.8 Utilizando el método de función de singularidad, se determina la pendiente en el punto\(C\) y la deflexión en el punto\(D\) de la viga con extremos sobresalientes, como se muestra en la Figura P7.17. \(EI\)= constante.

\(Fig. P7.17\). Viga.

7.9 Utilizando el método de función de singularidad, se determina la pendiente en el punto\(A\) y la deflexión en el punto\(B\) de la viga que se muestra en la Figura P7.18. \(EI\)= constante.

\(Fig. P7.18\). Viga.