9.4: El filtro de Kalman

La ubicación de un robot está sujeta a incertidumbre debido al deslizamiento de las ruedas y al ruido del codificador. Aprendimos en el pasado cómo la varianza en la posición se puede derivar de la varianza de la transmisión del robot usando la ley de propagación de errores y la cinemática hacia adelante del robot. Se puede ver que este error aumenta continuamente a menos que el robot tenga observaciones adicionales, por ejemplo, de un objeto estático con ubicación conocida. Esta actualización se puede hacer formalmente usando la regla de Bayes, que relaciona la probabilidad de estar en una determinada posición dado que el robot ve una cierta característica con la probabilidad de ver esta característica en la ubicación hipotética. Por ejemplo, un robot que conduce hacia una pared se volverá cada vez menos seguro de su posición (actualización de acción) hasta que encuentre la pared (actualización de percepción). Luego puede usar su modelo de sensor que relaciona su observación con posibles posiciones. Por lo tanto, su ubicación real debe estar en algún lugar entre su creencia original y donde el sensor le dice que esté. La regla de Bayes nos permite realizar esta ubicación para ubicaciones discretas y distribuciones de errores de sensores discretos. Esto es inconveniente ya que estamos acostumbrados a representar la posición de nuestro robot con una distribución gaussiana 2D. Además, parece mucho más fácil simplemente cambiar la media y varianzas de este gaussiano en lugar de actualizar cientos de variables. Los objetivos de esta sección son

• introducir una técnica conocida como filtro de Kalman para realizar actualizaciones de acción y percepción exclusivamente utilizando distribuciones gaussianas.
• para introducir formalmente la noción de un mapa de entidades.
• para desarrollar un ejemplo que ponga todo lo aprendido hasta ahora juntos: cinemática hacia adelante, propagación de errores y estimación de características.

Figura\(\PageIndex{1}\): Ejemplo de filtro de partículas. Las posibles posiciones y orientaciones del robot se distribuyen inicialmente de manera uniforme. Las partículas se mueven según el modelo de movimiento del robot. Las partículas que requerirían que el robot se mueva a través de una pared en ausencia de un evento de percepción de pared se eliminan (estrellas). Después de un evento de percepción, las partículas demasiado alejadas de una pared se vuelven improbables y sus posiciones son remutadas en las proximidades de una pared. Finalmente, el filtro de partículas converge.

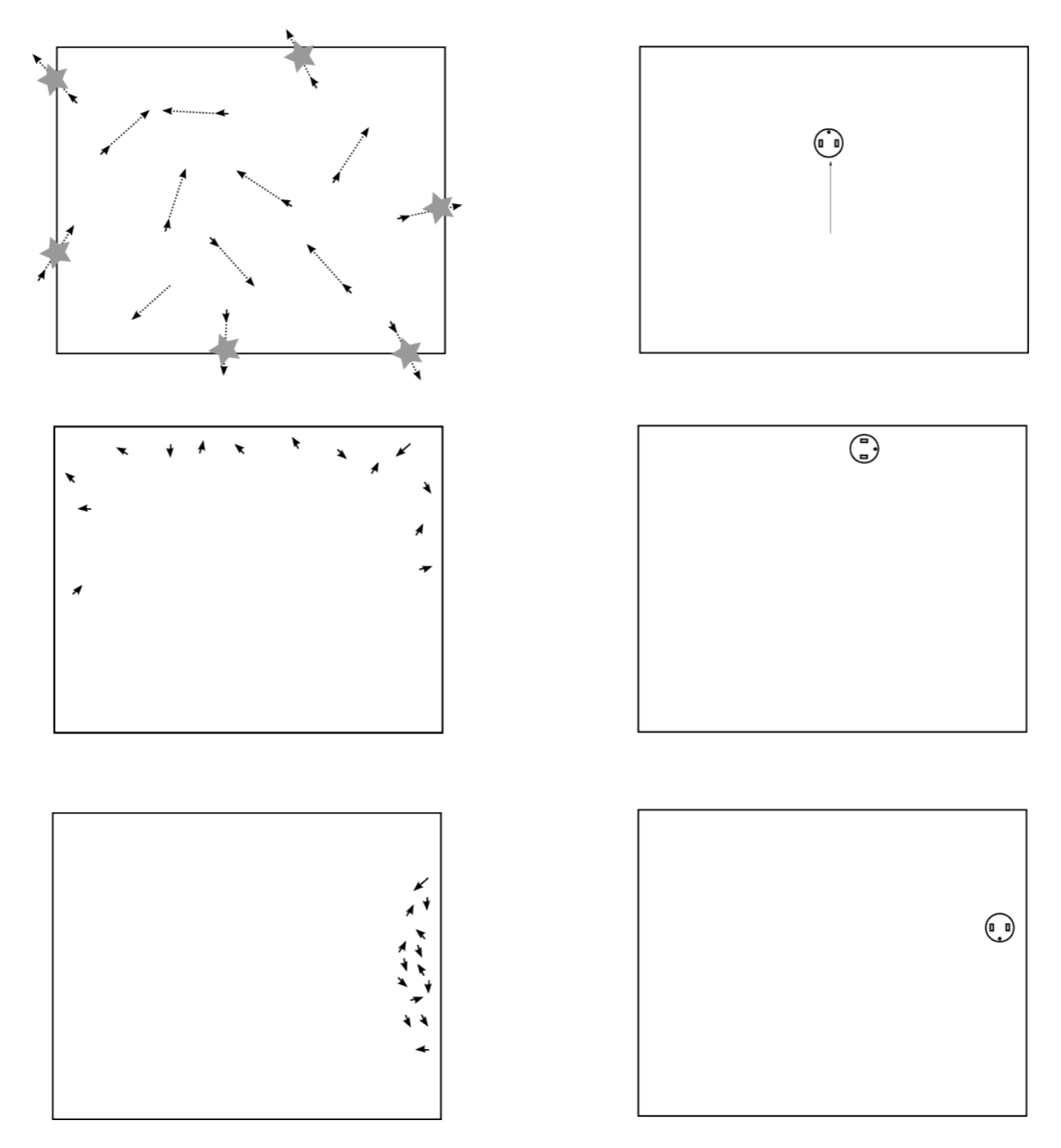
9.4.1. Localización probabilística basada en mapas

Para localizar un robot usando un mapa, necesitamos realizar los siguientes pasos

1. Calcular una estimación de nuestra nueva posición utilizando la cinemática hacia adelante y el conocimiento de las velocidades de las ruedas que enviamos al robot hasta que el robot encuentre alguna característica de identificación única.
2. Calcular la posición relativa de la entidad (una pared, un punto de referencia o baliza) con respecto al robot.
3. Utilice el conocimiento de dónde se encuentra la característica en coordenadas globales para predecir lo que el robot debe ver.
4. Calcula la diferencia entre lo que realmente ve el robot y lo que cree que debería ver.
5. Utilizar el resultado de (4) para actualizar su creencia ponderando cada observación con su varianza.

Los pasos 1-2 se basan en las secciones “Cinemática hacia adelante” y “Detección de líneas”. El paso 3 vuelve a utilizar una cinemática de avance simple para calcular la posición de una entidad almacenada en coordenadas globales en un mapa en coordenadas de robot. El paso 4 es una simple resta de lo que ve el sensor y lo que dice el mapa. El paso 5 introduce el filtro Kalman. Su derivación está involucrada, pero su intuición es simple: ¿por qué solo promediar entre donde creo que estoy y lo que me dicen mis sensores, si mis sensores son mucho más confiables y deberían llevar mucho más peso?

9.4.2. Fusión óptima de sensores

El filtro Kalman es una forma óptima de fusionar observaciones que siguen una distribución gaussiana. El filtro Kalman tiene una actualización y un paso de predicción. El paso de actualización utiliza un modelo dinámico del sistema (como la cinemática hacia adelante de su robot) y el paso de predicción utiliza un modelo de sensor (como la distribución de errores calibrada a partir de sus sensores). El filtro Kalman no sólo actualiza el estado del sistema (la posición del robot) sino también su varianza. Para ello, requiere el conocimiento de todas las varianzas involucradas en el sistema (por ejemplo, deslizamiento de rueda y error del sensor) y las utiliza para pesar cada medición en consecuencia. Antes de proporcionar las ecuaciones para el filtro de Kalman, haremos uso de un ejemplo sencillo que explica lo que significa “óptimo” en este contexto.

Sea q ₁ y q ₂ dos estimaciones diferentes de una variable aleatoria y σ ² ₁ y σ ^₂ sus varianzas, respectivamente. Que q sea el verdadero valor. Esta podría ser la posición del robot, e.g. Las observaciones tienen diferentes varianzas cuando se obtienen por diferentes medios, digamos usando la odometría para q ₁ y usando la ubicación de una característica conocida para q ₂. Ahora podemos definir el error cuadrático medio ponderado

\[S=\sum_{i=1}^{n}\frac{1 }{\sigma_{i}}(q-q̂_{i})^{2}\]

es decir, S es la suma de los errores de cada observación _qi ponderada por su desviación estándar σ _i. Cada error se pondera con su desviación estándar para poner más énfasis en las observaciones cuya desviación estándar es baja. Minimizar S para n = 2 produce la siguiente expresión óptima para q:

\[q=\frac{q̂_{1}\sigma _{2}^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}+\frac{q̂_{2}\sigma _{1}^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}\]

o, equivalentemente,

\[q=q̂_{1}+\frac{\sigma _{1}^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}(q̂_{2}-q̂_{1})\]

Ahora hemos derivado una expresión para fusionar dos observaciones con diferentes errores que de manera demostrable minimiza el error entre nuestra estimación y el valor real. Como q es una combinación lineal de dos variables aleatorias (Sección C.4, la nueva varianza viene dada por

\[\sigma ^{2}=\frac{1}{\frac{1}{\sigma _{1}^{2}}+\frac{1}{\sigma _{2}^{2}}}\]

Curiosamente, la varianza resultante es menor que ambos σ ₁ y σ ₂, es decir, agregar observación adicional siempre ayuda a reducir la precisión en lugar de introducir más incertidumbre.

9.4.3. Integración de predicción y actualización: El filtro de Kalman

Si bien hemos introducido el problema anterior como fusionar dos observaciones de la misma cantidad y ponderarlas por su varianza, también podemos interpretar la ecuación anterior como un paso de actualización que calcula una nueva estimación de una observación basada en su estimación anterior y una medición. Recuerda el paso (4) desde arriba: q2 − q1 no es otra cosa que la diferencia entre lo que el robot realmente ve y lo que piensa que debería ver. Este término se conoce como innovación en la lingo de Kalman. Ahora podemos reescribir (9.4.3) desde arriba en

\[x̂_{k+1}=x̂_{k}+K_{k+1}y_{k+1}\]

Aquí, _xk es el estado que nos interesa en el tiempo k, K _k+1 = σ ² ₁/(σ ² ₁ +σ ² ₂) la ganancia de Kalman, y _{k +1} = _q2 − _q1 la innovación. Desafortunadamente, son pocos los sistemas que nos permitan medir directamente la información que nos interesa. Más bien, obtenemos una medición de sensor z _k que necesitamos convertir a nuestro estado de alguna manera. También puedes pensar en esto al revés y predecir tu medida z _k a partir de tu estado x _k. Esto se hace usando el modelo de observación H _k, de manera que

\[y_{k}=z_{k}-H_{k}x_{k}\]

En nuestro ejemplo H _k era solo la matriz de identidad; en un problema de estimación de posición de robot H _k es una función que predeciría cómo vería un robot una determinada característica. Como puedes ver, toda la ponderación basada en varianzas se realiza en la ganancia Kalman K. El paso de actualización de percepción que se muestra arriba, también conocido como paso de predicción es solo la mitad de lo que hace el filtro de Kalman. El primer paso es el paso de actualización, que corresponde a la actualización de acción que ya conocemos. De hecho, la actualización de varianza en el filtro de Kalman es exactamente la misma que aprendimos durante la propagación de errores. Antes de entrar en más detalles sobre el filtro Kalman, es hora de un breve descargo de responsabilidad: el filtro Kalman solo funciona para sistemas lineales. La cinemática directa de incluso los robots más simples es en su mayoría no lineal, y también lo son los modelos de observación que relacionan las observaciones de los sensores y la posición del robot. Los sistemas no lineales se pueden tratar con el Filtro Kalman Extendido.