6.4: Tornillos Eléctricos

Última actualización
Guardar como PDF

Page ID: 83797

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un tornillo de potencia (también llamado a veces tornillo de avance) es otra máquina simple que se puede utilizar para crear fuerzas muy grandes. El tornillo puede pensarse como una cuña o una rampa que se ha enrollado alrededor de un eje. Al sostener una tuerca estacionaria y girar el eje, podemos hacer que la tuerca se deslice hacia arriba o hacia abajo de la cuña en el eje. De esta manera, un momento relativamente pequeño en el eje puede provocar fuerzas muy grandes en la tuerca.

Una sidra que consiste en un cubo de madera y un marco conectados por un tornillo metálico grande, girado girando un mango grande en forma de rueda. — Figura\(\PageIndex{1}\): El tornillo en esta sidra se gira con el mango en la parte superior. La tuerca estacionaria en el marco de la prensa fuerza el eje hacia abajo a medida que se gira. Imagen de Dominio Público por Daderot.

Un gato de tijera que se utiliza para subir o bajar un automóvil. — Figura\(\PageIndex{2}\): Al girar el tornillo en este gato de tijera, el usuario puede mover la tuerca (en el extremo izquierdo) más cerca o más lejos del anclaje en el extremo derecho, que elevará o bajará el automóvil. Imagen de Dominio Público por nrjfalcon1.

Análisis estático de tornillos de potencia:

La forma más fácil de analizar un sistema de tornillo de potencia es convertir el problema en un problema 2D “desenvolviendo” la rampa alrededor del eje. Para ello necesitaremos dos números. Primero necesitaremos el diámetro del eje, y segundo necesitaremos ya sea los hilos por pulgada/centímetro o el paso del tornillo. Los hilos por pulgada te indican cuántos hilos tienes por pulgada/centímetro de tornillo. Con un diseño de una sola rosca (la mayoría de los tornillos), esta también será la cantidad de veces que la rosca se enrolla alrededor del tornillo en una pulgada/centímetro. El paso, por otro lado, te da la distancia entre dos roscas adyacentes. Cualquiera de estos números se puede utilizar para encontrar el otro.

Una vez que tenemos estos números, podemos imaginarnos desenvolviendo la rampa alrededor del tornillo y terminando con una rampa en una de las dos situaciones siguientes. En cualquier caso, podemos usar la función tangente inversa para encontrar el ángulo de avance, que se puede considerar como el ángulo de la rosca que la tuerca está subiendo. Encontrar el ángulo de avance es el primer paso para analizar un sistema de tornillo de potencia.

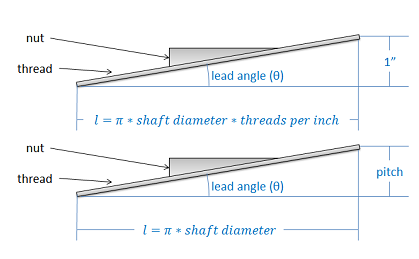
Dos copias de una representación 2D de un tornillo de potencia, con la rosca representada como una línea recta inclinada hacia arriba de izquierda a derecha, la tuerca representada como un triángulo rectángulo cuya hipotenusa está en contacto con el lado superior de la rosca, y el ángulo de avance (theta) como el ángulo que hace la rosca por encima del horizontal. En una versión del diagrama, la distancia vertical que cubre la rosca se da como 1 pulgada, y la distancia horizontal que cubre (l) es el producto de pi, el diámetro del eje y las roscas por pulgada. En la otra versión, la distancia vertical que cubre la rosca viene dada por el paso, y l es el producto de pi y el diámetro del eje. — Figura\(\PageIndex{3}\): El ángulo de avance de un tornillo es el ángulo de la rosca que la tuerca va a subir a medida que gira el eje.

Una vez que encontremos el ángulo de avance, podemos dibujar un diagrama de cuerpo libre de la “tuerca” en nuestro sistema sin envolver. Aquí incluimos la fuerza de empuje que está empujando nuestra tuerca hacia arriba por la pendiente, la fuerza de carga que es la fuerza que la tuerca ejerce sobre algún cuerpo externo, la fuerza normal entre la tuerca y el tornillo, y la fuerza de fricción entre la tuerca y el tornillo.

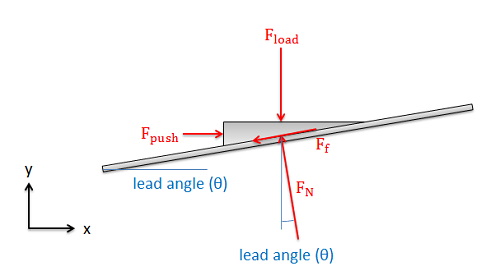
Diagrama de cuerpo libre de la tuerca del diagrama de tornillo de potencia en la Figura 3 anterior. La tuerca, que apunta hacia la derecha, experimenta una fuerza de empuje en su base, una fuerza de carga hacia abajo en su lado plano (que mira hacia arriba y no está en contacto con la rosca), una fuerza de fricción hacia abajo y hacia la izquierda a lo largo de su lado en contacto con la rosca, y una fuerza normal apuntando hacia arriba y hacia la izquierda que hace un ángulo con la vertical que es igual al ángulo de avance (theta). — Figura\(\PageIndex{4}\): El diagrama de cuerpo libre de la “tuerca” en nuestro sistema de tornillo de potencia, con un sistema de\(xy\) coordenadas de orientación estándar.

Si nuestro tornillo está empujando una carga a cierta velocidad constante, entonces podemos asumir dos cosas: Primero, la tuerca está en equilibrio, así podemos escribir las ecuaciones de equilibrio para la tuerca. Segundo, la tuerca se desliza, lo que indica que la fuerza de fricción será igual a la fuerza normal multiplicada por el coeficiente cinético de fricción.

\[ F_f = \mu_k * F_N \]

\[ \sum F_x = F_{push} - F_N * \sin (\theta) - \mu_k * F_N * \cos (\theta) = 0 \]\[ \sum F_y = F_{push} - F_N * \cos (\theta) - \mu_k * F_N * \sin (\theta) = 0 \]

Entonces podemos simplificar las ecuaciones anteriores en una sola ecuación que relaciona la fuerza de carga y la fuerza de empuje.

\[ F_{push} = \frac{\sin (\theta) + \mu_k * \cos (\theta)}{\cos (\theta) - \mu_k * \sin (\theta)} * F_{load} \]

En realidad, la fuerza de empuje no es una sola fuerza en absoluto. Son las fuerzas que impiden que la tuerca gire con el tornillo. La fuerza de empuje acumulativa realmente provocará un momento igual y opuesto al momento de entrada que está girando el eje.

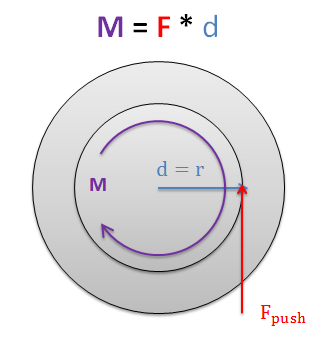
Diagrama que muestra la tuerca como un círculo más pequeño concéntrico con el eje. La fuerza de empuje se aplica hacia arriba en el borde derecho de la tuerca, creando un momento en el sentido de las agujas del reloj alrededor del centro del círculo cuya magnitud es igual al producto del radio de la tuerca y la magnitud de la fuerza de empuje. — Figura\(\PageIndex{5}\): La fuerza de empuje es realmente solo una representación de las fuerzas que impiden que la tuerca gire. Si la tuerca no está girando, entonces estas fuerzas deben causar un momento igual y opuesto al par que está impulsando el tornillo.

Por último, si reemplazamos la fuerza de empuje con el momento que está impulsando el tornillo en nuestro sistema (en este caso el par\(T\)), podemos relacionar el par de entrada que está impulsando nuestro tornillo con la fuerza con la que la tuerca en el tornillo está presionando hacia adelante. Los sistemas de tornillo generalmente están diseñados para permitir momentos de entrada bastante pequeños para empujar fuerzas de carga muy grandes.

\[ T = \frac{\sin (\theta) + \mu_k \cos (\theta)}{\cos (\theta) - \mu_k \sin (\theta)} * F_{load} * r_{shaft} \]

Tornillos Autoblocantes

Imagina que aplicamos un torque a un tornillo de potencia para levantar un cuerpo; luego cuando llevamos la carga a la altura deseada dejamos de aplicar ese par para dejar que el cuerpo se asiente donde está. Si tuviéramos que volver a dibujar nuestro diagrama de cuerpo libre desde antes para la nueva situación, encontraríamos dos cosas.

Falta la fuerza de empuje (ya que ya no se aplica un par al eje).
La fricción ahora está luchando contra la tuerca que se desliza de nuevo por la rampa.

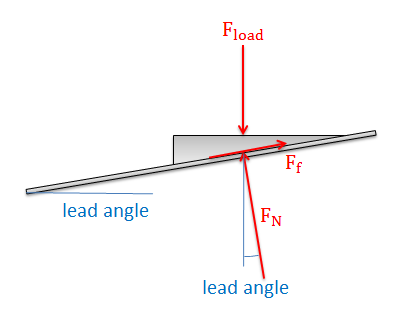
El diagrama de cuerpo libre de la Figura 4 anterior, pero con la fuerza de empuje eliminada y con la fuerza de fricción apuntando ahora hacia arriba a lo largo de la pendiente de la rosca. — Figura\(\PageIndex{6}\): Sin la fuerza de empuje de un par aplicado, la fuerza de fricción actúa para evitar que la tuerca se deslice por la rampa.

Con este nuevo diagrama de cuerpo libre, existen dos posibles escenarios que podrían ocurrir:

La fuerza de fricción es lo suficientemente grande como para evitar que la tuerca se deslice por la rampa, lo que significa que todo permanecerá en equilibrio estático si se libera.
La fuerza de fricción no será suficiente para evitar que la tuerca se deslice por la rampa, lo que significa que la carga comenzaría a caer tan pronto como se retire el par del eje.

Con aplicaciones de tornillo de potencia como un gato para automóvil, la segunda opción podría ser muy peligrosa. Por lo tanto, es importante saber si un sistema de tornillo de potencia es autobloqueante (escenario 1 anterior) o no autobloqueante (escenario 2 anterior).

Para definir el límite entre los sistemas de autobloqueo y los sistemas no autoblocantes, utilizamos algo llamado ángulo de autobloqueo. Como nos diría la intuición, el deslizamiento no ocurre en pendientes muy suaves (pequeños ángulos de avance) mientras que sí ocurre en pendientes muy pronunciadas (grandes ángulos de avance). El ángulo en el que la tuerca comenzaría a deslizarse se conoce como el ángulo de autobloqueo.

Para encontrar el ángulo de autobloqueo, asumiremos un movimiento inminente (relacionando la fuerza de fricción con la fuerza normal) y dejaremos el ángulo de avance como desconocido. Esto nos permite crear el diagrama de cuerpo libre como se muestra a continuación y nos da las ecuaciones de equilibrio a continuación.

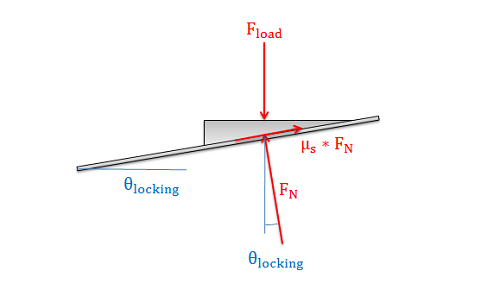
El diagrama de cuerpo libre de la Figura 6 anterior, con la fuerza de fricción expresada como el coeficiente de fricción estática multiplicado por la fuerza normal y el ángulo de avance, así como el ángulo que hace el vector de fuerza normal con la vertical, siendo etiquetado como el ángulo de bloqueo (theta_locking). — Figura\(\PageIndex{7}\): Para encontrar el ángulo de autobloqueo asumiremos un movimiento inminente. Luego dibujamos nuestro diagrama de cuerpo libre (arriba) y escribimos nuestras ecuaciones de equilibrio (abajo) en consecuencia.

\[ \sum F_x = - F_N * \sin (\theta) + \mu_s * F_N * \cos (\theta) = 0 \]\[ \sum F_y = -F_{load} + F_N * \cos (\theta) + \mu_s * F_N * \sin (\theta) = 0 \]

Usando la ecuación de\(x\) equilibrio como punto de partida, podemos resolver para el ángulo\(\theta\) (eliminando la fuerza normal todos juntos en el proceso). Esta nueva ecuación que se muestra a continuación nos da el ángulo de autobloqueo. \[ \theta_{locking} = \tan ^{-1} (\mu_s) \]

Los sistemas con ángulos de derivación más pequeños que este serán autobloqueantes, mientras que los sistemas con ángulos de avance mayores que este no serán autobloqueantes.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/mci-kH14JGw.

Ejemplo\(\PageIndex{1}\)

El tornillo de potencia de abajo se está utilizando para levantar una plataforma con un peso de 12 libras. Con base en la siguiente información...

¿Cuál es el par requerido en el eje para levantar la carga?
¿Caería la carga si se quitara el toque del eje?

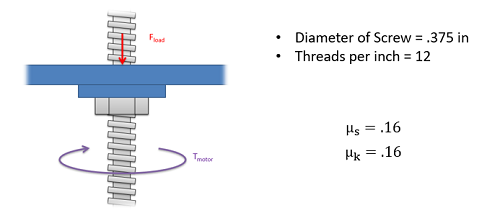
Un tornillo de potencia que se utiliza para levantar una plataforma. El diámetro del tornillo es de 0.375 pulgadas, los hilos por pulgada es de 12 y el coeficiente de fricción estática y cinética es de 0.16. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un tornillo de potencia con un diámetro de tornillo de 0.375 pulgadas, 12 roscas por pulgada, se utiliza para levantar una plataforma, con un coeficiente de fricción estática y cinética de 0.16.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/uB2r3AtxCRs.