Saltar al contenido principal
LibreTexts Español

7.1: Movimiento continuo unidimensional

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    83939

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Imagina que tenemos una partícula que se mueve a lo largo de un solo eje. En cualquier momento dado, esta partícula tendrá una posición, que podremos cuantificar con un solo número al que llamaremos\(x\). Este valor medirá la distancia desde algún punto de origen establecido hasta la posición de la partícula. Si la partícula se mueve con el tiempo, necesitaremos una función para describir la posición a lo largo del tiempo\(x(t)\). Esta es una ecuación donde si tapamos un valor para\(t\), nos dará la posición en ese momento.

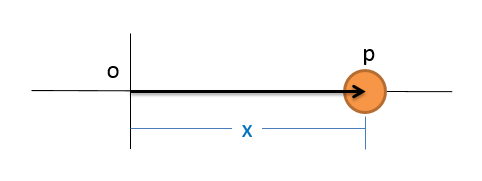
    Una partícula en el lado positivo de un eje x, con su posición dada como la distancia x desde el origen.
    Figura\(\PageIndex{1}\): La posición de una partícula en una dimensión se puede describir con un solo número. Si la posición cambia con el tiempo, utilizaremos la función\(x(t)\) para describir la posición en cualquier momento dado.

    La velocidad de la partícula es entonces la velocidad de cambio de la posición a lo largo del tiempo. Si la partícula no se mueve, entonces la posición no cambia con el tiempo y la velocidad es cero. Si la partícula se mueve, primero necesitaremos encontrar la ecuación para la posición\(x(t)\), y luego tomar la derivada de la ecuación de posición para encontrar la ecuación de velocidad\(v(t)\). La velocidad difiere de la velocidad en que la velocidad tiene una dirección (ya sea positiva o negativa por ahora) mientras que la velocidad es simplemente la magnitud de la velocidad (siempre un número positivo).

    Lo siguiente es la aceleración, que es la tasa de cambio de la velocidad a lo largo del tiempo. Si la velocidad no está cambiando, la aceleración será cero. Si la velocidad cambia con el tiempo, entonces tendremos que tomar la derivada de la ecuación de velocidad\(v(t)\) para encontrar la ecuación de aceleración\(a(t)\). La aceleración es entonces también la doble derivada de la ecuación de posición a lo largo del tiempo. Al igual que la velocidad, la aceleración tiene tanto una magnitud como una dirección.

    Para simplificar la notación, a menudo usamos un punto en la parte superior de la variable para indicar una derivada de tiempo. Esto hace que la velocidad (la derivada de\(x\))\(\dot{x}\) y la aceleración (la derivada de la derivada de\(x\))\(\ddot{x}\). Estas relaciones y sus anotaciones de taquigrafía se muestran a continuación.

    \ begin {align}\ text {Posición:}\ quad &\, x (t)\\\ text {Velocidad:}\ quad &\, v (t) =\ frac {dx} {dt} =\ punto {x}\\ texto {Aceleración:}\ quad &\, a (t) =\ frac {dv} {dt} =\ frac {d^2 x} {dt^2} =\ ddot {x}\ end {align}

    Si en cambio comenzamos con la ecuación para la aceleración, podemos tomar la integral de esa ecuación\(a(t)\) para encontrar la ecuación para la velocidad,\(v(t)\). Pero a diferencia de los derivados, tendremos un paso extra en este proceso porque cada vez que nos integramos terminamos con una constante de integración (a la que normalmente llamaremos\(C\)). Cuando integramos la ecuación de aceleración para encontrar la ecuación de velocidad, esta constante será la velocidad inicial (la velocidad en el tiempo = 0).

    A continuación podemos tomar la integral de la ecuación de velocidad\(v(t)\) para encontrar la ecuación de posición\(x(t)\). Con esta integración volveremos a terminar con una constante de integración, que en este caso será la posición inicial (la posición en el tiempo = 0). Estas relaciones se muestran a continuación.

    \ begin {align}\ text {Aceleración:}\ quad &\, a (t)\\\ text {Velocidad:}\ quad &\, v (t) =\ int a (t)\\\ text {Posición:}\ quad &\, x (t) =\ int v (t) =\ iint a (t)\ end {align}

    Sistemas de aceleración constante:

    En los casos en los que tenemos una aceleración constante (muchas veces debido a una fuerza constante), podemos comenzar con un valor constante para\(a(t) = a\), y calcular las integrales a partir de ahí. En el camino agregaremos la velocidad inicial y la posición inicial como las constantes de integración para terminar con las fórmulas a continuación.

    \ begin {align}\ text {Aceleración:}\ quad &\, a (t) = a\\\ text {Velocidad:}\ quad &\, v (t) = en + v_0\\ text {Posición:}\ quad &\, x (t) =\ frac {1} {2} a t^2 + v_0 t + x_0\ end {align}

    Si tomamos las ecuaciones para la posición y la velocidad desde arriba, luego resolvemos ambas\(t\) y establecemos esas ecuaciones iguales entre sí, en realidad podemos terminar con otra ecuación que relaciona directamente la posición, la velocidad y la aceleración sin necesidad de saber el tiempo.

    \[ v^2 - v_0^2 = 2a(x - x_0) \]

    Es importante recordar que estas ecuaciones sólo son válidas cuando la aceleración es constante. Cuando ese no es el caso, necesitará usar cálculo para encontrar las derivadas o integrales basadas en las ecuaciones de posición, velocidad y aceleración que sí conoce.

    Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/uemxYyLN3-U.
    Ejemplo\(\PageIndex{1}\)

    Estás en una camioneta que acelera de manera constante de 20 m/s a 35 m/s en el transcurso de 10 segundos. ¿Cuál es su tasa de aceleración?

    Una camioneta negra que se mueve rápidamente por una carretera de la ciudad, con un fondo borroso.
    Figura\(\PageIndex{2}\): Una camioneta negra acelerando a un ritmo constante.
    Solución
    Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/19qGXfNkWcQ.
    Ejemplo\(\PageIndex{2}\)

    Estás en una camioneta que acelera de manera constante de 20 m/s a 35 m/s en el transcurso de 10 segundos. ¿Cuántos metros viajaste en esos diez segundos?

    Una camioneta negra que se mueve rápidamente por una carretera de la ciudad, con un fondo borroso.
    Figura\(\PageIndex{3}\): Una camioneta negra acelerando a un ritmo constante.
    Solución
    Video\(\PageIndex{3}\): Solución trabajada a Ejemplo\(\PageIndex{2}\), proporcionada por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/hjyUHnw8FSI.
    Ejemplo\(\PageIndex{3}\)

    En un experimento de desaceleración de trineo con cohetes, un trineo tripulado se desacelera de una velocidad de 200 mph (89.4 m/s) a una parada a una velocidad constante de 18 G's (176.6 m/s 2). ¿Cuánto tiempo tarda en detenerse el trineo? ¿Qué tan lejos viaja el trineo mientras desacelera?

    Un trineo cohete que viajaba a lo largo de una pista, emitiendo humo negro desde la parte trasera.
    Figura\(\PageIndex{4}\): Un trineo cohete desacelerando a una velocidad constante.
    Solución
    Video\(\PageIndex{4}\): Solución trabajada a Ejemplo\(\PageIndex{3}\), proporcionada por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/bXzcdpaxB_c.
    Ejemplo\(\PageIndex{4}\)

    Una partícula metálica se acelera en un campo magnético de tal manera que su velocidad a lo largo del tiempo es definida por la función\(v(t) = 4t^2 - 12\), donde el tiempo es en segundos y la velocidad es en metros por segundo. Si asumimos que la partícula tiene una posición inicial de cero\((x_0 = 0)\), ¿cuáles son las ecuaciones que describen la aceleración y la posición a lo largo del tiempo?

    Un acelerador de partículas que utiliza campos magnéticos para aumentar la velocidad de las partículas.
    Figura\(\PageIndex{5}\): Un acelerador de partículas.
    Solución
    Video\(\PageIndex{5}\): Solución trabajada a Ejemplo\(\PageIndex{4}\), proporcionada por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/AWhLmMhKygg.

    This page titled 7.1: Movimiento continuo unidimensional is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.