7.2: Movimiento no continuo unidimensional

Última actualización
Guardar como PDF

Page ID: 83940

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En movimiento continuo, utilizamos una sola función matemática cada una para describir la posición, velocidad o aceleración a lo largo del tiempo. Si no podemos describir el movimiento con una sola función matemática durante todo el período de tiempo, ese movimiento se considera movimiento no continuo. En casos como este, utilizaremos diferentes ecuaciones para diferentes secciones del periodo de tiempo general.

Para un ejemplo de movimiento no continuo, imagina un automóvil que acelera por unos segundos, luego mantiene una velocidad constante durante unos segundos, luego frena y se detiene en los últimos segundos. No hay una función matemática que podamos usar para describir el movimiento para el período de tiempo completo, pero si dividimos el movimiento en tres partes, entonces podemos llegar a una ecuación para cada sección del movimiento.

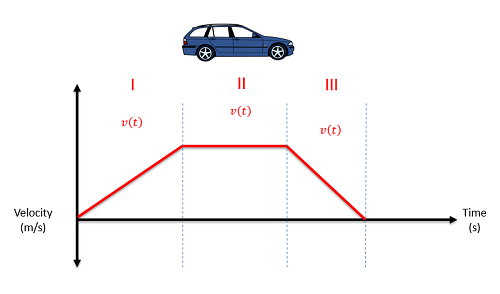
Gráfico de la velocidad de un automóvil en metros por segundo contra el tiempo en segundos: comenzando desde el origen, primero aumenta a una tasa consistente durante el Periodo 1, luego se mantiene en un valor constante para el Período 2, y finalmente disminuye hasta cero a una tasa consistente diferente durante el Período 3. — Figura\(\PageIndex{1}\): A medida que este auto acelera, su velocidad sube constantemente por unos segundos, luego se mantiene constante durante unos segundos, luego baja de manera constante por unos segundos. Dado que necesitaríamos una ecuación separada para cada sección de este movimiento, esto se considera movimiento no continuo.

Analizar el primer periodo de tiempo será exactamente lo mismo que analizar una función continua. Inicialmente necesitaremos identificar la función matemática para describir la posición, o velocidad, o aceleración para ese primer período de tiempo. A continuación tomamos derivadas para movernos de la posición a la velocidad a la aceleración o tomamos integrales para pasar de la aceleración a la velocidad a la posición. Siempre que tomamos una integral, debemos recordar incluir la constante de integración que representará la velocidad inicial o la posición inicial (en las ecuaciones de velocidad y posición, respectivamente).

Para la segunda, tercera, y cualquier otra sección siguiente, haremos mucho el mismo proceso. Comenzaremos identificando una ecuación para la posición, o velocidad, o aceleración para ese período de tiempo. A partir de ahí nuevamente tomamos derivados o integrales según corresponda, pero ahora las constantes de integración serán un poco más complicadas. Esas constantes siguen representando velocidades y posiciones iniciales en cierto sentido, pero serán la velocidad y posición cuando\(t=0\), no la velocidad y posición al inicio de esa sección.

Para encontrar las constantes de integración, vamos a tener que usar el punto de transición, que es el punto en el tiempo en el que estamos pasando de un conjunto de ecuaciones al siguiente. A pesar de que las ecuaciones están cambiando, no podemos tener un salto instantáneo ni en la posición ni en la velocidad. Un salto instantáneo en cualquier posición o velocidad requeriría una aceleración infinita, lo cual es físicamente imposible.

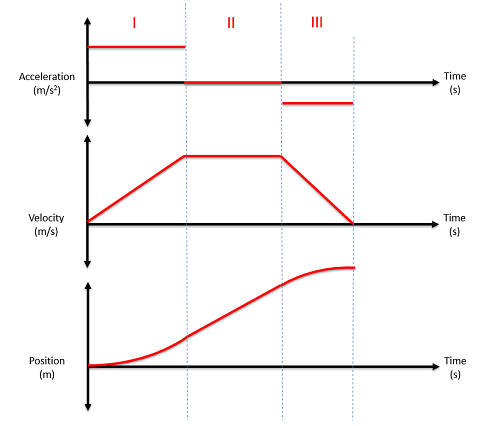
Gráficas que muestran la aceleración, velocidad y posición del carro de la Figura 1 anterior como funciones de tiempo en segundos. La posición inicial se representa como 0 metros. — Figura\(\PageIndex{1}\). Aunque hay saltos notables en la aceleración moviéndose de una sección a la siguiente, no hay saltos en la velocidad o posición a medida que avanzamos de una sección a la siguiente. Esto se debe a que los saltos en esas parcelas requerirían infinitas aceleraciones.

Para encontrar las ecuaciones de velocidad para el segundo marco de tiempo (o tercero, cuarto, etc.), comenzamos integrando la ecuación de aceleración para ese mismo periodo de tiempo. Esto conducirá a una ecuación con una constante desconocida de integración. Para resolver esa constante, miramos hacia atrás a la ecuación de velocidad para el marco de tiempo anterior y resolvemos para la velocidad al final de este período de tiempo anterior. Como no puede saltar instantáneamente, esta es también la velocidad al inicio del periodo de tiempo actual. Usando esta velocidad, junto con el tiempo\(t\) en el punto de transición, podemos resolver para lo último desconocido en la ecuación de velocidad actual (la constante de integración).

Para encontrar la ecuación de posición para el segundo marco de tiempo (o tercero, cuarto, etc.), comenzamos integrando la ecuación de velocidad para el mismo período de tiempo (primero deberá resolver las incógnitas en la ecuación de velocidad, como se discutió anteriormente). Después de la integración, debemos tener una nueva constante de integración en la ecuación de posición. Al igual que hicimos con las ecuaciones de velocidad, usaremos la ecuación de posición del marco de tiempo anterior para resolver la posición en el punto de transición, luego usaremos ese valor junto con el tiempo conocido\(t\) para resolver la constante desconocida en la ecuación de posición actual.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/yNBenQRalhU.

Ejemplo\(\PageIndex{1}\)

Un automóvil acelera desde el reposo a una velocidad de 10 m/s ² durante 10 segundos. El automóvil entonces inmediatamente comienza a desacelerar a una velocidad de 4 m/s ² durante otros 25 segundos antes de llegar a un alto. Encuentre las ecuaciones para las funciones de aceleración, velocidad y posición durante el período de tiempo completo de 35 segundos y grafique estas funciones.

Un coche de carreras rojo en una pista. — Figura\(\PageIndex{3}\): Un coche de carreras rojo que se mueve a lo largo de una pista.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/tPBlDQsiX_c.

Ejemplo\(\PageIndex{2}\)

Un avión con una velocidad inicial de 95 m/s aterriza en una pista. Para el primer segundo el avión rueda sin desacelerar. Para los siguientes 5 segundos se aplica empuje inverso, desacelerando el plano a una velocidad de 4 m/s ². Finalmente, los frenos se aplican con empuje inverso aumentando la tasa de desaceleración a 8 m/s ². ¿Cuánto tiempo tarda el avión en detenerse por completo? ¿A qué distancia recorre el avión antes de llegar a una parada completa?

Un avión que se mueve a lo largo de una pista. — Figura\(\PageIndex{4}\): Un avión se mueve por una pista de aeropuerto.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/Of-ipYWblrQ.

Ejemplo\(\PageIndex{3}\)

El movimiento de un satélite se describe mediante la función de velocidad que se muestra a continuación durante un período de tiempo de sesenta segundos. Para ese mismo periodo de tiempo, determine las funciones de aceleración y posición del satélite y dibuje estas funciones en una parcela.

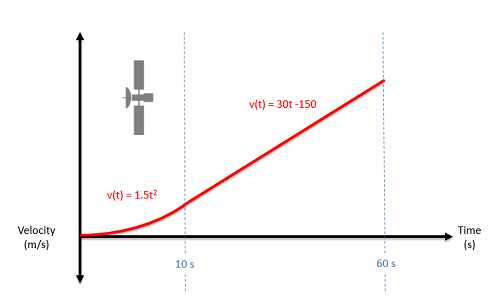
Gráfico de la velocidad del satélite (en metros por segundo) vs tiempo (en segundos) durante 60 segundos. La velocidad comienza en el origen y es descrita por la función 1.5*t^2 durante los primeros 10 segundos, y por la función 30*t-150 durante los 50 segundos restantes. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Gráfico de la velocidad de un satélite en m/s por un periodo de 60 segundos, con las funciones que describen la velocidad dada.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/ngI6_I8VFPs.