10.3: Colisiones unidimensionales de partículas

Última actualización
Guardar como PDF

Page ID: 83950

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El Método Impulso-Momentum es particularmente útil cuando se examinan colisiones entre cuerpos. Al examinar los cuerpos que colisionan como un sistema de partículas, como los dos cuerpos que chocan por debajo, los impulsos ejercidos por las fuerzas internas, o las fuerzas ejercidas entre dos cuerpos dentro del sistema, serán iguales y opuestos y de ahí se cancelarán en nuestra ecuación impulso-impulso.

Dos bolas de billar que acaban de chocar entre sí. La fuerza ejercida sobre la primera bola por la segunda es idéntica en magnitud pero opuesta en dirección a la fuerza ejercida sobre la segunda bola por la primera. — Figura\(\PageIndex{1}\): Cuando dos cuerpos chocan, la Tercera Ley de Newton asegura que las fuerzas normales de la colisión siempre serán iguales y opuestas. Esto significa que los impulsos serán iguales y opuestos y se cancelarán en nuestra ecuación impulso-impulso al examinar el sistema de ecuaciones.

Debido a que las fuerzas impulsivas de la colisión son tan grandes durante el muy corto período de la colisión, otras fuerzas externas suelen considerarse insignificantes. Esto quiere decir que para nuestra colisión, no hay impulso externo y por lo tanto no hay cambio en la suma de los momentos de los cuerpos. Esto se conoce como la conservación del impulso, y se mantendrá cierto para todo tipo de colisiones.

\[ \sum \vec{J} = 0 = \sum m \vec{v}_f - \sum m \vec{v}_i \]

\[ \sum m \vec{v}_f - \sum m \vec{v}_i \]

En el caso de la colisión de dos cuerpos, cuerpo A y cuerpo B en este caso, podemos descomponer las sumas de la siguiente manera. Los subíndices en este caso se están utilizando para denotar tanto el cuerpo (A o B) como los estados inicial versus final (antes o después de la colisión).

\[ m_A \ \vec{v}_{A,f} + m_B \ \vec{v}_{B,f} = m_A \ \vec{v}_{A,i} + m_B \ \vec{v}_{B,i} \]

Además de la ecuación de conservación del impulso, también generaremos normalmente una segunda ecuación que podamos usar junto con la conservación del impulso. Sin embargo, esta segunda ecuación dependerá del tipo de colisión, siendo los tres posibles tipos de colisión elásticos, inelásticos y semielásticos.

Colisiones Elásticas

Una colisión elástica es una colisión en la que se supone que toda la energía se conserva como energía cinética. En realidad, las verdaderas colisiones elásticas no existen ya que alguna energía siempre se convertirá en calor o sonido, pero en la práctica dos cuerpos muy rígidos que chocan sin mucha deformación pueden acercarse mucho al ideal de una colisión elástica. Un ejemplo de una colisión que está cerca de elástico es un conjunto de bolas de billar colisionando, como en la Figura\(\PageIndex{1}\).

Una colisión elástica conserva energía además del impulso, por lo que la ecuación de conservación de energía será nuestra segunda ecuación que usemos para complementar la conservación del impulso.

\[ \frac{1}{2} m_A \ \vec{v}_{A,f}^2 + \frac{1}{2} m_B \ \vec{v}_{B,f}^2 = \frac{1}{2} m_A \ \vec{v}_{A,i}^2 + \frac{1}{2} m_B \ \vec{v}_{B,i}^2 \]

Colisiones inelásticas

Una colisión inelástica es lo opuesto a una colisión elástica, en que gran parte de la energía del sistema se pierde en la deformación de los cuerpos. De hecho, en una colisión inelástica los cuerpos deben deformarse de tal manera que se peguen juntos después de la colisión. Con los dos cuerpos pegados entre sí, tendrán velocidades finales coincidentes.

\[ \vec{v}_{A,f} = \vec{v}_{B,f} \]

Colisión Semielástica

Finalmente, cualquier cosa entre una colisión elástica y una colisión inelástica se considera una colisión semielástica. Se trata de una colisión donde se conserva menos del cien por ciento de la energía cinética, pero los objetos no se pegan juntos después de la colisión. En casos de colisiones semielásticas, utilizaremos algo llamado el coeficiente de restitución (generalmente denotado por la letra griega épsilon,\(\epsilon\)), para complementar nuestra ecuación de conservación del impulso.

El coeficiente de restitución es un número entre 0 y 1 que mide la “rebote” de los dos cuerpos en la colisión. Específicamente, para un solo cuerpo que rebota en una superficie rígida, el coeficiente de restitución se define como el negativo de la velocidad después de rebotar en la superficie dividido por la velocidad antes de rebotar en la superficie. \[ \epsilon = - \frac{v_f}{v_i} \]

Una colisión perfectamente elástica tendría un coeficiente de restitución de uno (no se perdería velocidad), mientras que una colisión totalmente inelástica tendría un coeficiente de restitución de cero. Todas las demás colisiones tendrán un coeficiente de restitución que se encuentra en algún punto intermedio.

Para los casos en que dos cuerpos rebotan uno del otro, simplemente usaríamos velocidades relativas en lugar de la velocidad de un solo cuerpo. Usando la velocidad del cuerpo A relativa a la velocidad del cuerpo B, se nos ocurre la siguiente ecuación.

\[ \epsilon = - \frac{\vec{v}_{f, A/B}}{\vec{v}_{i, A/B}} = - \frac{\vec{v}_{f,A} - \vec{v}_{f,B}}{\vec{v}_{i,A} - \vec{v}_{i,B}} \]

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/lFZ8Mr4Vcow.

Ejemplo\(\PageIndex{1}\)

Una bola blanca que pesa 0.17 kg, que viaja a 1 m/s, impacta una bola de billar estacionaria con una masa de 0.15kg como se muestra a continuación. Si las bolas chocan directamente y la colisión es elástica, ¿cuáles serán las velocidades después de la colisión (ignorar las energías rotacionales)?

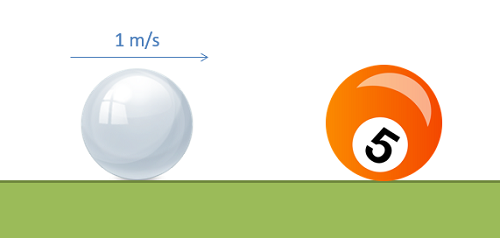
Una bola blanca a la izquierda y una bola de billar a la derecha, ambas sobre una superficie plana. La bola blanca viaja directamente hacia la bola de billar estacionaria, a la velocidad de 1 m/s. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una bola blanca que viaja a 1 m/s impacta directamente con una bola de billar estacionaria.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/n1g5RwuFYJI.

Ejemplo\(\PageIndex{2}\)

Una bala de 4.2 g que viaja a 965 m/s se aloja en un tronco estacionario con una masa de 1.5 kg.

¿Cuál es la velocidad del tronco y la bala inmediatamente después de la colisión?
¿Qué porcentaje de la energía cinética se perdió en la colisión?

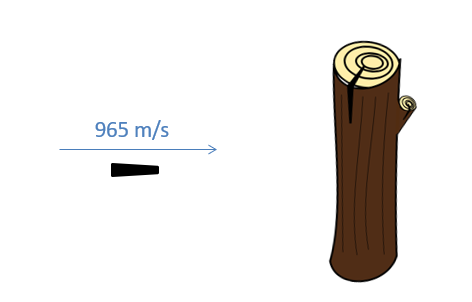
Una bala en el lado izquierdo de la imagen, con una velocidad de 965 m/s, se desplaza directamente hacia un tronco de árbol en el lado derecho de la imagen. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Una bala que viaja a 965 m/s está volando directamente hacia un tronco grande, donde quedará alojada.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/FyyziesH9LI.

Ejemplo\(\PageIndex{3}\)

Dos masas en una varilla sin fricción, como se muestra a continuación, se establecen para impactar entre sí. Si el coeficiente de restitución entre los objetos es 0.6, ¿cuál es la velocidad de cada cuerpo después de la colisión?

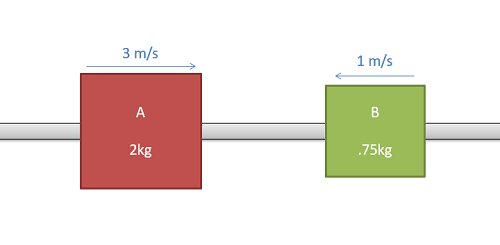
Una masa de 2 kg etiquetada A, en el lado izquierdo de la imagen, se enrosca a través de una varilla y se mueve hacia la derecha a 3 m/s. Una masa de 0.75 kg etiquetada B, en el lado derecho de la imagen, se enrosca a través de la misma varilla y se mueve hacia la izquierda a 1 m/s. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Dos masas diferentes ensartadas en una varilla sin fricción viajan una hacia la otra a diferentes velocidades.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/MOUG_7BqcLY.