11.1: Rotación de Eje Fijo en Cuerpos Rígidos

Al pasar de la cinemática de partículas a la cinemática de cuerpo rígido, agregamos la rotación de un cuerpo al proceso de análisis de movimiento. Algunos cuerpos se trasladarán y girarán al mismo tiempo, pero muchos sistemas diseñados tienen componentes que simplemente giran alrededor de algún eje fijo. Comenzaremos nuestro examen de la cinemática del cuerpo rígido examinando estos problemas de rotación de eje fijo, donde la rotación es el único movimiento del que debemos preocuparnos.

Figura\(\PageIndex{1}\): El volante de inercia de este motor antiguo es un buen ejemplo de rotación de eje fijo.

Figura\(\PageIndex{2}\): El tubo de rayos X giratorio dentro del pórtico de esta máquina de TC es otro ejemplo de rotación de eje fijo. Imagen de Trece de Clubes, CC-BY-SA 2.0.

Posición angular, velocidad y aceleración:

Al igual que con el movimiento traslacional, tendremos posiciones angulares de las cuales podremos tomar la derivada para encontrar velocidades angulares, de las cuales podremos tomar nuevamente la derivada de para encontrar aceleraciones angulares. Dado que solo podemos tener un solo eje de rotación en problemas bidimensionales (girando alrededor del\(z\) eje, siendo las rotaciones en sentido contrario a las agujas del reloj positivas y las rotaciones en sentido horario negativas) las ecuaciones reflejarán las ecuaciones unidimensionales utilizadas en la cinemática de partículas.

\ begin {align}\ text {Posición angular:}\ quad &\,\ theta (t)\\\ text {Velocidad angular:}\ quad &\,\ omega (t) =\ frac {d\ theta} {dt} =\ punto {\ theta}\\ texto {Aceleración angular:}\ quad &\,\ alpha (t) =\ frac {d\ omega} {dt} =\ frac {d^2\ theta} {dt^2} =\ ddot {\ theta}\ end {align}

También como con el movimiento traslacional unidimensional, podemos usar la integración para movernos en la dirección opuesta (solo recuerda tus constantes de integración).

\ begin {align}\ text {Aceleración:}\ quad &\,\ alpha (t)\\\ text {Velocidad:}\ quad &\,\ omega (t) =\ int\ alpha (t)\, dt\\ text {Posición:}\ quad &\,\ theta (t) =\ int\ omega (t)\, dt =\ int\ int\ alpha (t)\, dt\, dt\ end {align}

Si tenemos aceleraciones angulares constantes, también podemos usar las siguientes fórmulas adaptadas a partir del movimiento unidimensional.

\ begin {align}\ text {Aceleración:}\ quad &\,\ alpha (t) =\ alfa\\ [5pt]\ text {Velocidad:}\ quad &\,\ omega (t) =\ alfa t +\ omega_0\\ [5pt]\ text {Posición:}\ quad &\,\ theta (t) =\ frac {1} {2}\ alpha t^2 +\ omega_0 t +\ theta_0\\ [5pt]\ texto {Sin tiempo:}\ quad &\,\ omega^2 -\ omega_0^2 = 2\ alfa (\ theta -\ theta_0)\ end {align}

Velocidad y aceleración de un punto en un cuerpo giratorio:

Con rotación de eje fijo, hay un solo punto en un cuerpo que no se mueve; sin embargo, todos los demás puntos de este cuerpo tendrán cierta velocidad y cierta aceleración debido a la rotación del propio cuerpo.

Figura\(\PageIndex{3}\): El diagrama anterior muestra un punto P en un cuerpo que gira alrededor del eje fijo O. El punto P está a una\(r\) distancia constante del punto fijo O. Adaptaremos las ecuaciones de cinemática polar para encontrar la velocidad y aceleración del punto P en cualquier instante dado.

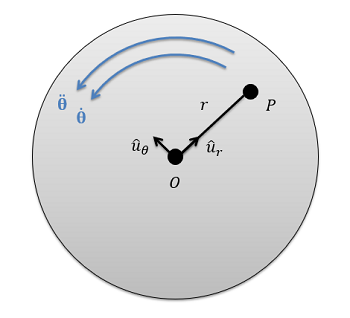
Para determinar las velocidades y aceleraciones de estos puntos, adaptaremos las ecuaciones que utilizamos para las coordenadas polares. Como recordatorio, estas ecuaciones fueron las siguientes:

\ begin {align}\ text {Velocidad:}\ quad &\, v =\ punto {r}\ hat {u} _r + r\ punto {\ theta}\ hat {u} _\ theta\\ text {Aceleración:}\ quad &\, a = (\ ddot {r} - r\ punto {\ theta} ^2)\ hat {u} _r + (2\ punto {r}\ punto {\ theta} + r\ ddot {\ theta})\ sombrero {u} _ {\ theta}\ end {align}

Para simplificar las ecuaciones anteriores, podemos señalar que para un cuerpo rígido, el punto P nunca se acerca ni se aleja más del punto central fijo O. Esto significa que la distancia\(r\) nunca cambia, y los\(\ddot{r}\) términos\(\dot{r}\) y en las ecuaciones anteriores son cero. Poniendo esto a trabajar, podemos simplificar las ecuaciones anteriores en las siguientes ecuaciones.

\ begin {align}\ text {Velocidad:}\ quad &\, v = r\ punto {\ theta}\ hat {u} _ {\ theta}\\ texto {Aceleración:}\ quad &\, a = (-r\ punto {\ theta} ^2)\ hat {u} _r + (r\ ddot {\ theta})\ hat {u} _ {theta}\ end {align}

Estas ecuaciones nos permiten encontrar la velocidad y aceleración de cualquier punto en un cuerpo que gira alrededor de un eje fijo, dado que conocemos la velocidad angular del cuerpo\((\dot{\theta)\), la aceleración angular del cuerpo\((\ddot{\theta})\), y la distancia del punto al eje de rotación\((r)\).

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/X02-jN5cwF4.

Ejemplo\(\PageIndex{1}\)

Un volante gira sobre un eje fijo en una máquina de vapor. El volante gira a una velocidad de 600 rpm antes de que un freno comience a desacelerar el volante a una velocidad constante de 30 rad/s ². ¿Cuál es el tiempo necesario para detener por completo el volante? ¿Cuántas rotaciones atraviesa el volante mientras desacelera?

Figura\(\PageIndex{4}\): El volante de una máquina de vapor gira sobre un eje fijo.

Solución

Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/z1S9O0XFkDE.

Ejemplo\(\PageIndex{2}\)

Un plato de disco duro de 8 cm de diámetro gira a una velocidad constante de 3600 rpm. ¿Cuál es la velocidad de un punto en el borde exterior del plato? ¿Cuál es la aceleración que experimenta un punto en el borde del plato?

Figura\(\PageIndex{5}\): Un plato de disco duro gira con su centro fijo en su lugar.

Solución

Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/n4OixdyqqoU.