13.1: Conservación de Energía para Cuerpos Rígidos

Última actualización
Guardar como PDF

Page ID: 84022

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los conceptos de Trabajo y Energía proporcionan la base para resolver una variedad de problemas cinéticos. Generalmente, este método se llama Método Energético o Conservación de Energía, y puede reducirse a la idea de que el trabajo realizado a un cuerpo será igual al cambio de energía de ese cuerpo. Dividiendo la energía en piezas de energía cinética y potencial como lo hacemos a menudo en problemas de dinámica, llegamos a la siguiente ecuación base para la conservación de energía.

\[ W = \Delta KE + \Delta PE \]

Es importante notar que a diferencia de la Segunda Ley de Newton, la ecuación anterior no es una ecuación vectorial. No necesita ser desglosado en componentes que puedan simplificar el proceso. Sin embargo, solo tenemos una sola ecuación y por lo tanto solo podemos resolver para un solo desconocido, lo que puede limitar este método.

Trabajo en Problemas de Cuerpo Rígido:

Para el trabajo realizado a un cuerpo rígido, debemos considerar cualquier fuerza aplicada sobre una distancia como lo hicimos para las partículas, así como cualquier momento ejercido sobre algún ángulo de rotación. Si se trata de fuerzas constantes y momentos constantes, simplemente multiplicamos la fuerza por la distancia y el momento por el ángulo de rotación para encontrar el trabajo general realizado en el problema. Al igual que con las partículas, estos son los componentes de las fuerzas en la dirección de desplazamiento, con fuerzas que se oponen al movimiento contando como trabajo negativo. De igual manera, se trata de momentos en el sentido de rotación, con momentos opuestos a la rotación contando como trabajo negativo. Ambos tipos de trabajo son aditivos, y todo el trabajo se agrupa para su análisis.

\[ W = F * d + M * \Delta \theta \]

En instancias de fuerzas no constantes y momentos no constantes, necesitaremos integrar las fuerzas y momentos sobre la distancia recorrida y el ángulo de rotación, respectivamente.

\[ W = \int \limits_{x_1}^{x_2} F(x) \, dx + \int \limits_{\theta_1}^{\theta_2} M(\theta) \, d \theta \]

Energía:

En cuerpos rígidos, al igual que con las partículas, vamos a romper la energía en energía cinética y energía potencial. La energía cinética es la masa de energía en movimiento, mientras que la energía potencial representa la energía que se almacena debido a la posición o tensiones en un cuerpo.

En su forma de ecuación, la energía cinética de un cuerpo rígido está representada por la mitad de la masa del cuerpo por su velocidad al cuadrado, más la mitad del momento másico de inercia por la velocidad angular al cuadrado. Si queremos determinar el cambio en la energía cinética, simplemente tomaríamos la energía cinética final menos la energía cinética inicial.

\[ KE = \frac{1}{2} m v^2 + \frac{1}{2} I \omega^2 \]

\[ \Delta KE = \left( \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2 \right) + \left( \frac{1}{2} I \omega_f^2 - \frac{1}{2} I \omega_i^2 \right) \]

La energía potencial, a diferencia de la energía cinética, no es realmente energía en absoluto. En cambio, representa el trabajo que una fuerza dada potencialmente hará entre dos instantes en el tiempo. La energía potencial puede venir de muchas formas, pero las dos que discutiremos aquí son la energía potencial gravitacional y la energía potencial elástica. Estos representan el trabajo que harán la fuerza gravitacional y una fuerza de resorte, respectivamente. A menudo usamos estos términos de energía potencial en lugar del trabajo realizado por gravedad o resortes respectivamente. Al incluir estos términos de energía potencial, es importante no incluir también el trabajo realizado por la gravedad o las fuerzas de resorte.

El cambio en la energía potencial gravitacional para cualquier sistema está representado por la masa del cuerpo, multiplicado por el valor\(g\) (9.81 m/s ² o 32.2 pies/s ² en la superficie terrestre), multiplicado por el cambio vertical de altura entre la posición inicial y la posición final. En forma de ecuación, esto es como sigue. \[ \Delta PE = m * g * \Delta h \]

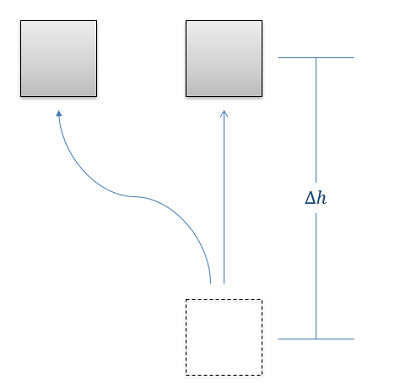
Un contorno punteado de una caja en la parte inferior de la imagen, que representa la posición original de la caja. En la parte superior de la imagen, dos cajas idénticas se alinean horizontalmente. Uno se movió recto hacia arriba desde su posición original, mientras que el otro tomó un camino curvo para llegar a la parte superior de la página, pero la distancia vertical recorrida (Delta h) es la misma para ambas casillas. — Figura\(\PageIndex{1}\): Al encontrar el cambio en la energía potencial gravitacional, multiplicamos la masa del objeto por\(g\) (dándonos el peso del objeto) y luego multiplicamos eso por el cambio en la altura del objeto, independientemente del camino tomado.

A diferencia del trabajo y la energía cinética, no existe una versión rotacional de la energía potencial gravitacional, así que esto es exactamente lo mismo que teníamos para las partículas.

Para determinar el cambio en la energía potencial elástica, tendremos que identificar cualquier resorte lineal (como lo tuvimos para las partículas), así como cualquier resorte torsional y las constantes de resorte para cada uno de estos resortes.

Una trampa para ratones con una base de madera y una mandíbula que se cierra de golpe debido a la acción de un resorte cuando se toca el gatillo. — Figura\(\PageIndex{2}\): El resorte torsional en esta trampa para ratones libera su energía potencial elástica para cerrar la trampa. Imagen de dominio público por Evan-Amos.

Para encontrar el cambio en la energía potencial elástica, necesitaremos conocer la rigidez de cualquier resorte en el problema (representado por\(k\), en unidades de fuerza por distancia para resortes lineales o momento por ángulo de torsión para resortes torsionales) así como la distancia o ángulo sobre el que se ha estirado el resorte o por debajo de su posición natural de descanso. Esta diferencia con respecto a la posición de reposo se representa por la distancia\(x\) para los resortes lineales o el ángulo\(\theta\) para los resortes de torsión. Una vez que tenemos esos valores, la energía potencial elástica se puede calcular multiplicando la mitad de la rigidez por la distancia al\(x\) cuadrado o el ángulo al\(\theta\) cuadrado. Para encontrar el cambio en la energía potencial elástica, simplemente tomamos la energía potencial elástica final menos la energía potencial elástica inicial.

\[ \Delta PE_{linear \ spring} = \frac{1}{2} k \ x_f^2 - \frac{1}{2} k \ x_i^2 \]

\[ \Delta PE_{torsional \ spring} = \frac{1}{2} k \ \theta_f^2 - \frac{1}{2} k \ \theta_i^2 \]

Volviendo a nuestra ecuación original de conservación de energía, simplemente tapamos los términos apropiados en cada lado (trabajo a la izquierda y energías a la derecha) y equilibramos los dos lados para resolver cualquier incógnitas. Los términos que no existen o no cambian (como la energía potencial elástica en un problema sin resortes, o\(\Delta KE\) en un problema donde no hay cambio en la velocidad del cuerpo) se pueden poner a cero. Nuevamente, solo hay una ecuación, por lo que solo podemos resolver por un solo desconocido a menos que complementemos la ecuación de conservación de energía con otras ecuaciones de relación.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/YVkzjzHSW-g.

Ejemplo\(\PageIndex{1}\)

El tocadiscos de un tocadiscos consiste en un disco de 12 pulgadas de diámetro con un peso de 5 lbs. El motor acelera el tocadiscos desde el reposo hasta su velocidad de operación de 33.33 rpm en una rotación. ¿Cuál es el trabajo realizado por el motor? ¿Cuál es el par promedio que ejerció el motor?

Un tocadiscos de maleta. — Figura\(\PageIndex{3}\): Un tocadiscos en un tocadiscos. Imagen de Ron Clausen, CC-BY-SA 4.0.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/UPHgU-o80Q0.

Ejemplo\(\PageIndex{2}\)

Un sistema como se muestra a continuación se utiliza para ralentizar pasivamente el descenso de una puerta. El portón se puede aproximar como una placa plana en su borde con una masa de 25 kilogramos y una altura de 2 metros. Supongamos que el resorte no está estirado como se muestra en el diagrama.

¿Cuál sería la velocidad angular de la puerta sin el resorte?
Si queremos reducir la velocidad angular en la parte inferior al 25% de su valor original, ¿cuál debería ser la constante elástica?

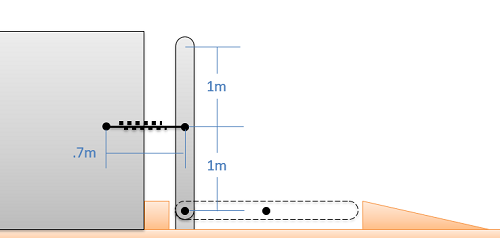
Una puerta se representa como una barra delgada de 2 metros de largo, actualmente en posición vertical con su borde inferior fijado a una bisagra. La puerta puede cerrarse cayendo a la derecha hasta que esté completamente horizontal. En su posición vertical actual, su punto medio está directamente alineado y unido a un resorte horizontal que sobresalga de una pared vertical ubicada a la izquierda de la puerta. El manantial, en su estado sin estirar, tiene 0.7 metros de largo. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Vista de arriba hacia abajo de una puerta con bisagras en una posición actualmente abierta, unida por un resorte a una pared que corre paralela a ella que ralentizará el movimiento de la puerta a medida que se cierra.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/HCAC0tNR18w.

Ejemplo\(\PageIndex{3}\)

Una bola esférica de 5 kilogramos con un radio de 0.05 metros se coloca en una rampa como se muestra a continuación. Si la bola rueda sin deslizarse, ¿cuál es la velocidad de la bola en la parte inferior de la rampa?

Una bola se encuentra en la parte superior de una rampa con una inclinación de ángulo desconocido, a 0.1 metros sobre el suelo. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una bola esférica se coloca en la parte superior de una rampa, a 0.1 metros sobre el suelo, y rueda sin resbalar.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/p2pvQ0kCWIU.

Ejemplo\(\PageIndex{4}\)

Se coloca un medio cilindro de 16 kilogramos sobre una superficie dura y plana como se muestra a continuación y se libera del reposo. ¿Cuál será la velocidad angular máxima, ya que oscila de un lado a otro?

Un cilindro de 50 cm de diámetro se corta por la mitad longitudinalmente y se orienta para que solo una base sea visible. Luego se coloca sobre borde, de manera que el borde plano de la base quede orientado hacia la izquierda y quede completamente vertical. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Un cilindro de 50 cm de diámetro se corta por la mitad longitudinalmente, luego se equilibra sobre una superficie plana y dura para que solo uno de sus bordes largos y rectos esté en contacto con dicha superficie.

Solución: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/HpRtDQjoEBA.

Ejemplo\(\PageIndex{5}\)

Un mecanismo consiste en dos ruedas de 3 kilogramos conectadas a una barra de 2 kilogramos como se muestra a continuación. Con base en las dimensiones del diagrama, ¿cuál es la velocidad inicial mínima requerida para las ruedas para asegurar que el mecanismo lo haga todo el camino a través de una rotación sin balancearse hacia atrás?

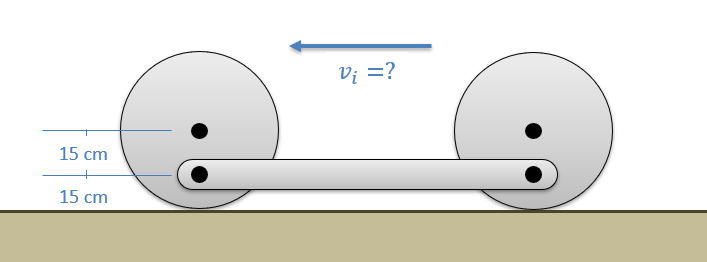
Dos ruedas idénticas, cada una con un radio de 30 cm, están conectadas con una barra que se fija a cada rueda en un punto a 15 cm del centro. Actualmente, las ruedas están ambas orientadas por lo que se minimiza la distancia entre la superficie plana en la que descansan las ruedas y los puntos de fijación para la barra. Al mecanismo se le da cierta velocidad inicial hacia la izquierda. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{5}\). Un par de ruedas están conectadas por una barra de longitud fija, lo que las obliga a rodar juntas.

Solución: Video\(\PageIndex{6}\): Solución trabajada a problema de ejemplo\(\PageIndex{5}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/8cjQ1S6yOTc.