15.1: Vibraciones libres sin amortiguar

Última actualización
Guardar como PDF

Page ID: 84046

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las vibraciones ocurren en sistemas que intentan regresar a su estado de reposo o equilibrio cuando se perturban, o se alejan de su estado de equilibrio. Las vibraciones más simples para analizar son las vibraciones sin amortiguar, libres con un grado de libertad.

“Sin amortiguar” significa que no hay pérdidas de energía con el movimiento (ya sea que las pérdidas sean intencionales, por agregar amortiguadores, o no intencionales, a través de arrastre o fricción). Un sistema sin amortiguar vibrará para siempre sin ninguna fuerza aplicada adicional. Un péndulo simple tiene una amortiguación muy baja, y oscilará durante mucho tiempo antes de detenerse. “Amortiguado” significa que hay fuerzas resistivas y pérdidas de energía con el movimiento que hacen que el sistema deje de moverse eventualmente.

“Libre” significa que, después de la perturbación inicial, las únicas fuerzas que actúan sobre el sistema son internas al sistema (resortes, amortiguadores) y/o gravedad. Un diapasón continúa vibrando después de la perturbación inicial de ser golpeado. En contraste, “forzado” significa que hay una fuerza externa, típicamente periódica, que actúa sobre el sistema. Un martillo neumático vibra debido a tener un suministro de aire comprimido que fuerza continuamente la broca hacia arriba y hacia abajo, y deja de vibrar muy rápidamente sin ese forzamiento periódico externo.

“Un grado de libertad” significa que solo consideraremos sistemas con una masa que vibra a lo largo de una dirección (por ejemplo, use variable\(x\)) o alrededor de un eje (por ejemplo, use variable\(\theta\)). Los sistemas que tienen más de una masa o que vibran a lo largo o alrededor de dos o más ejes tienen más de un grado de libertad.

Podemos derivar la ecuación del sistema configurando un diagrama de cuerpo libre. Considera una masa sentada sobre una superficie sin fricción, unida a una pared a través de un resorte.

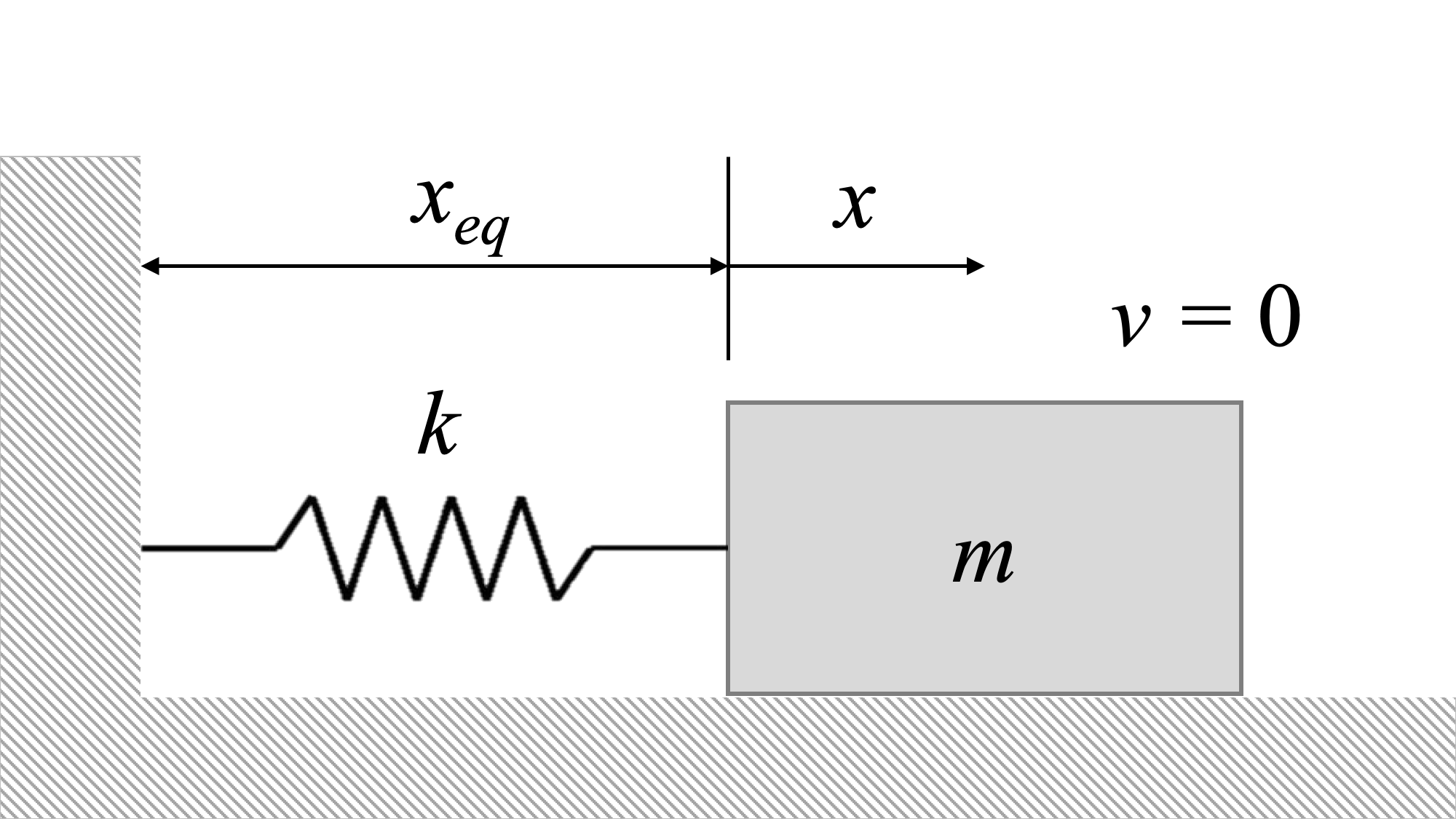
Un bloque de masa m está en reposo sobre una superficie plana. Un resorte de constante de resorte k está unido al lado izquierdo del bloque, y el extremo izquierdo de ese resorte está unido a una pared. La longitud actual del resorte, que está en equilibrio, es x_eq, y la dirección de aumentar x es hacia la derecha. — Figura\(\PageIndex{1}\): Se trata de un sistema que consiste en una masa unida a la pared a través de un resorte, que se asienta sobre una superficie sin fricción. El sistema se encuentra actualmente en equilibrio, y el resorte no se estira ni comprime.

El sistema anterior está en equilibrio. Está en reposo, y permanecerá en reposo a menos que alguna otra fuerza actúe sobre ella.

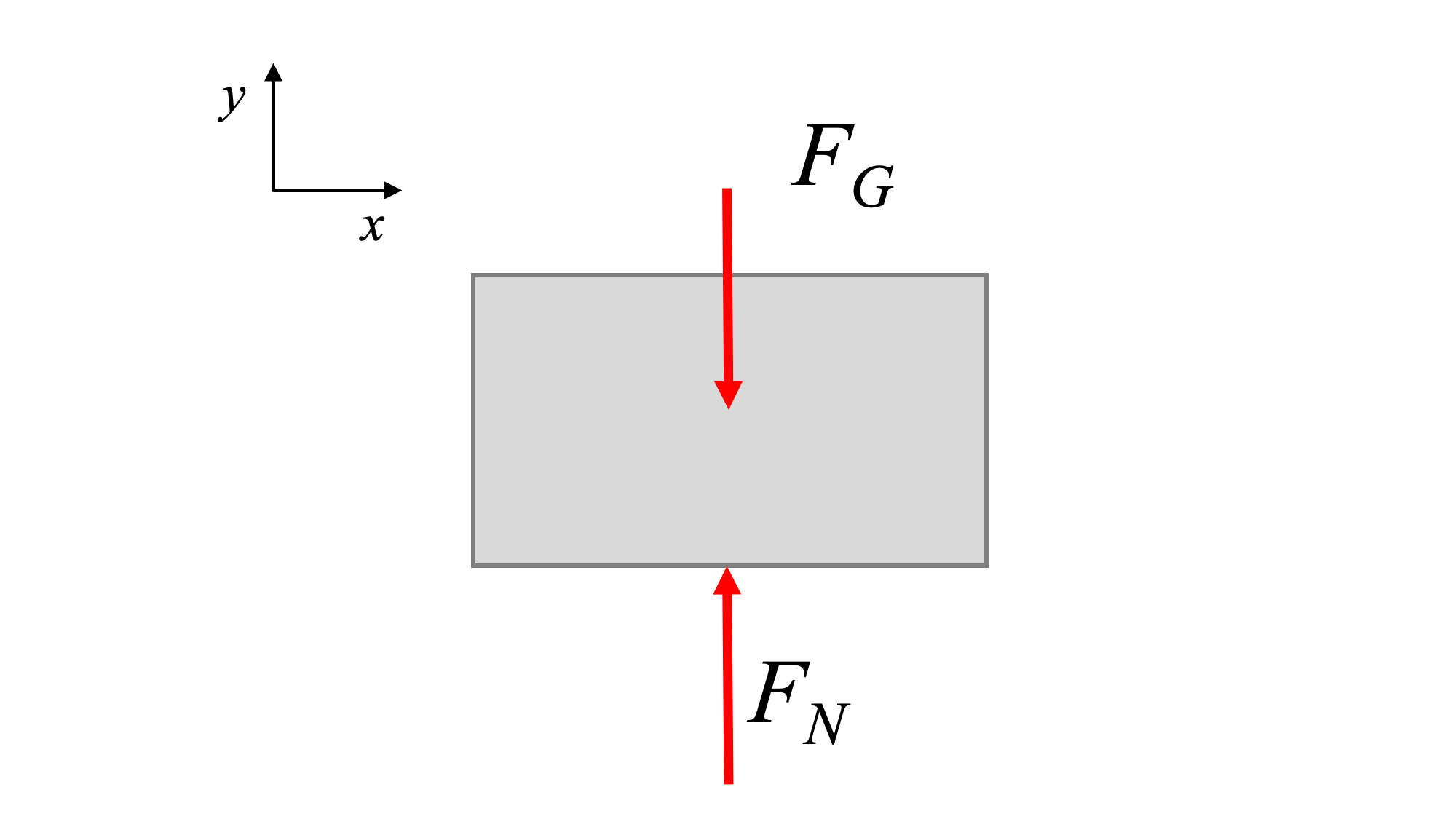
Diagrama de cuerpo libre de la masa rectangular de la Figura 1 anterior. Se experimenta una fuerza gravitacional hacia abajo de la Tierra, y una fuerza normal ascendente, de la misma magnitud, desde la superficie en la que está sentada. — Figura\(\PageIndex{2}\): Diagrama de cuerpo libre del sistema en posición de equilibrio. Dado que el resorte está en su longitud sin estirar, no produce fuerza.

Para iniciar el sistema vibrando, necesitamos perturbarlo. La perturbación está alejando el sistema del equilibrio en una pequeña cantidad.

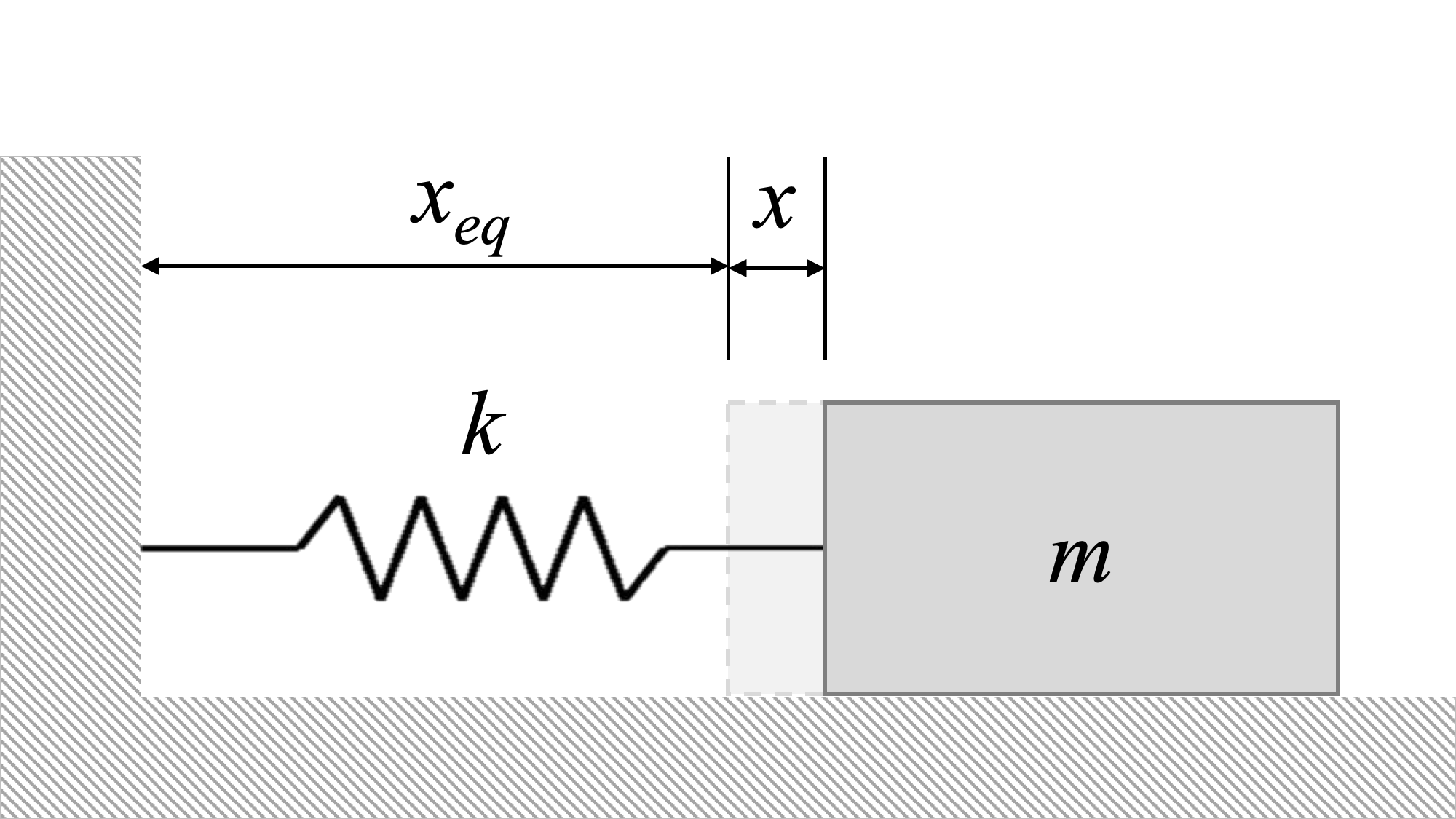
El sistema de la Figura 1 anterior tiene la masa movida una pequeña distancia x hacia la derecha desde su posición de equilibrio. — Figura\(\PageIndex{3}\): Sistema masa-resorte perturbado por una cantidad\(+x\) del equilibrio. Esto estira el resorte, provocando una fuerza de resorte que tiende a tirar de la masa hacia el equilibrio.

Cuando perturbimos este sistema, estiramos o comprimimos el resorte. Esto genera una fuerza de resorte, y la fuerza del resorte siempre está en una dirección que tiende a tirar del sistema hacia el equilibrio.

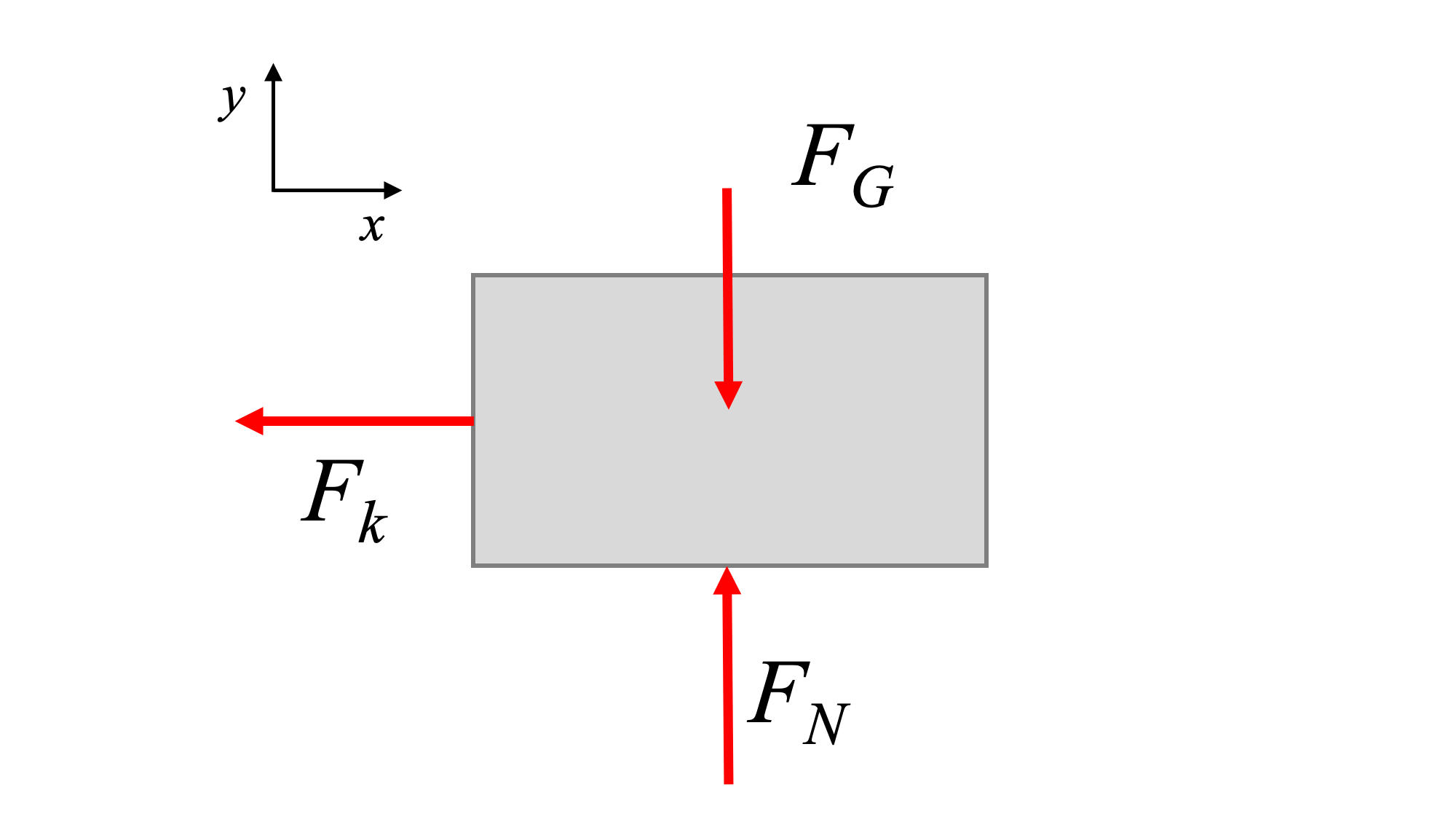
Diagrama de cuerpo libre de la masa de la Figura 3 anterior. Se experimenta una fuerza hacia abajo de la gravedad equilibrada por una fuerza normal ascendente desde la superficie en la que se asienta, así como una fuerza que apunta hacia la izquierda cuando el resorte estirado intenta regresar a su longitud de equilibrio. — Figura\(\PageIndex{4}\): Diagrama de cuerpo libre del sistema masa-resorte perturbado por una cantidad\(+x\) del equilibrio. Esto estira el resorte, provocando una fuerza de resorte que tiende a tirar de la masa hacia el equilibrio.

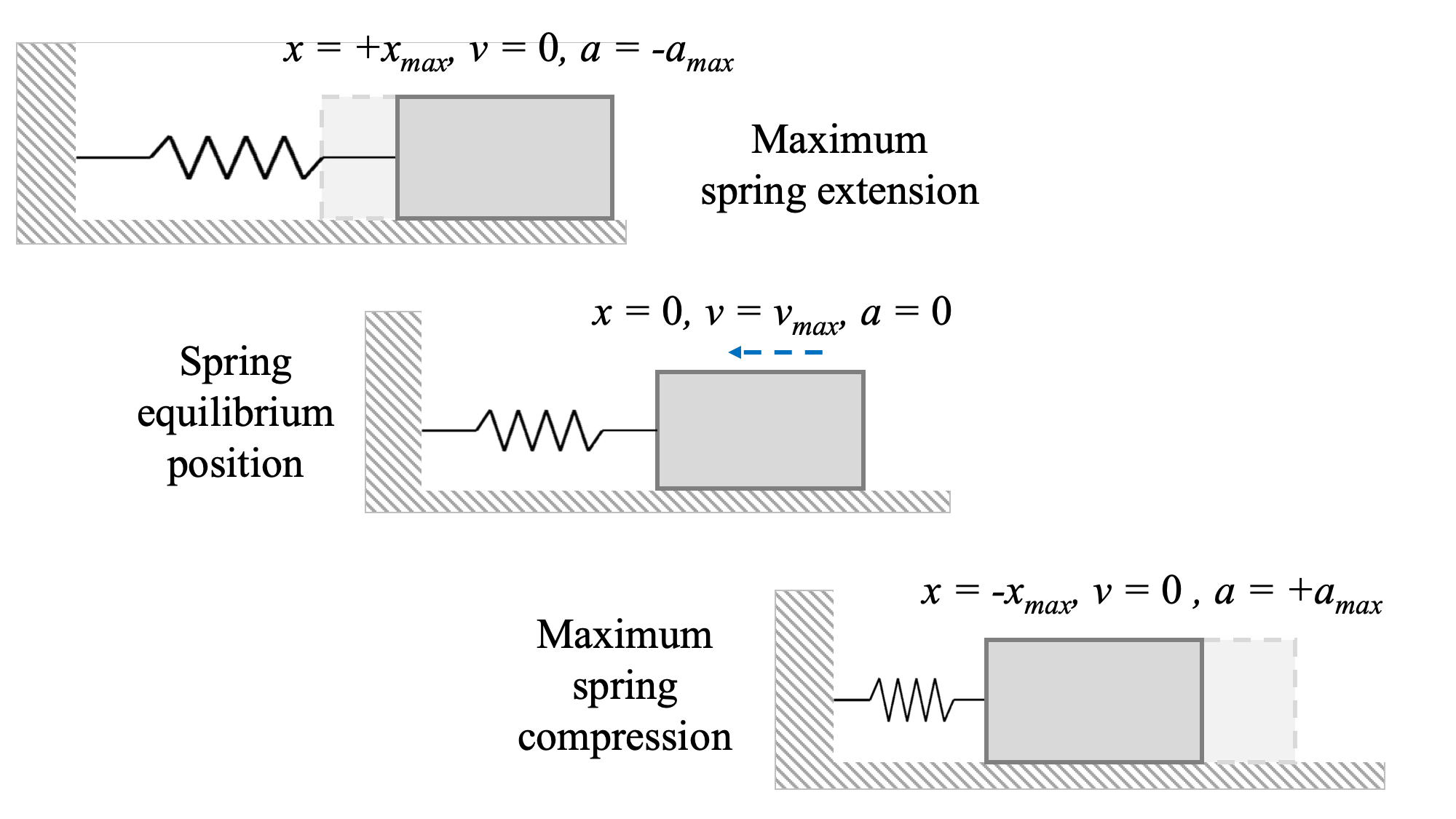
El sistema masa-resorte en tres posiciones diferentes, con sus respectivos valores de posición x, velocidad y aceleración, con valores positivos apuntando a la derecha y negativos a la izquierda. Una posición es la extensión máxima del resorte, donde x = x_max, v = 0 y a = -a_max. El segundo es la posición de equilibrio del resorte, donde x = 0, v = - v_max, y a = 0. La tercera posición es la compresión máxima del resorte, donde x = -x_max, v = 0, y a = a_max. — Figura\(\PageIndex{5}\): Vibración del sistema masa-resorte. Después de una perturbación inicial, el sistema oscila entre dos posiciones extremas (\(-x_{max}\)y\(x_{max}\)). Las posiciones extremas son puntos de respuesta donde la velocidad es cero, pero la fuerza del resorte está en un máximo (máximo estiramiento/compresión) y por lo tanto la aceleración es máxima. A medida que el sistema pasa por la posición de equilibrio, el resorte ya no se estira (fuerza cero, aceleración cero), sino que la velocidad está en su máxima (esto se puede determinar utilizando la conservación de energía) y la inercia del sistema lleva la masa más allá de la posición de equilibrio. En ausencia de amortiguación o de aplicación de otra fuerza, el sistema oscilará para siempre.

Podemos generar la ecuación de movimiento del sistema, y determinar los detalles de cómo vibrará, analizando este estado perturbado. Recordemos que la fuerza o momento del resorte es:

\[ \vec{F}_k = k \vec{x} \]

\[ \vec{M}_k = k \vec{\omega} \]

Tenga en cuenta que las constantes de resorte en las ecuaciones anteriores tienen diferentes unidades, dependiendo de si el resorte es lineal (Newton/metro) o torsional (Newton-metros/radianes), y que se\(\theta\) debe dar en radianes. La magnitud de la fuerza del resorte depende de\(x\), la distancia perturbada desde la longitud no estirada del resorte (no necesariamente la posición de equilibrio del sistema), y lo mismo es cierto para el momento de un resorte torsional. La fuerza o momento del resorte está en la dirección/orientación opuesta a la del desplazamiento. Es decir, si se tira de la masa hacia la derecha, la fuerza del resorte apunta hacia la izquierda.

El proceso para encontrar la ecuación de movimiento del sistema es el siguiente:

Esboce el sistema con una pequeña perturbación positiva (\(x\)o\(\theta\)).
Dibuja el diagrama de cuerpo libre del sistema perturbado. Asegúrese de que la fuerza del resorte tenga una dirección opuesta a la perturbación.
Encuentra la única ecuación de movimiento para el sistema en la coordenada perturbada usando la Segunda Ley de Newton. Mantenga la misma dirección positiva para la posición y asigne aceleración positiva en la misma dirección.
Mueva todos los términos de la ecuación a un lado y verifique que todos los términos sean positivos. Si todos los términos no son positivos, hay un error en la dirección de desplazamiento, aceleración y/o fuerza del resorte.

Para el sistema de ejemplo anterior, con constante de masa\(m\) y resorte\(k\), derivamos lo siguiente:

\[ \sum F_x = m a_x = m \ddot{x} \]

\[ -F_k = m \ddot{x} \]

\[ -kx = m \ddot{x} \]

\[ m \ddot{x} + kx = 0 \]

Esto nos da una ecuación diferencial que describe el movimiento del sistema. Podemos reescribirlo en forma normal:

\[ m \ddot{x} + kx = 0 \]

\[ \Rightarrow \ddot{x} + \frac{k}{m} x = 0 \]

\[ \Rightarrow \ddot{x} + \omega_n^2 x = 0 \]

El término\(\omega_n\) se denomina frecuencia natural angular del sistema, y tiene unidades de radianes/segundo.

\[ \omega_n^2 = \frac{k}{m} \]

\[ \omega_n = \sqrt{\frac{k}{m}} \]

Suponiendo que la perturbación inicial del sistema puede ser descrita por la posición y velocidad de la masa en\(t=0\), entonces:

\[ x(0) = x_0 \]

\[ v(0) = \dot{x}(0) = v_0. \]

La solución a la ecuación diferencial, que proporciona la posición\(x(t)\) del sistema en el momento\(t\), es:

\[ x(t) = C \sin \left( \omega_n t + \phi \right), \]

\[ \text{where:} \quad \omega_n = \sqrt{\frac{k}{m}}, \,\, C = \sqrt{ \left( \frac{v_0}{\omega_n} \right)^2 + x_0^2 }, \,\, \phi = \tan ^{-1} \left( \frac{x_0 \omega_n}{v_0} \right). \]

La amplitud\(C\) describe el desplazamiento máximo durante las oscilaciones (i.e.\(x_{max}\)), y la fase\(\phi\) describe cómo se desplaza la función sinusoidal en el tiempo.

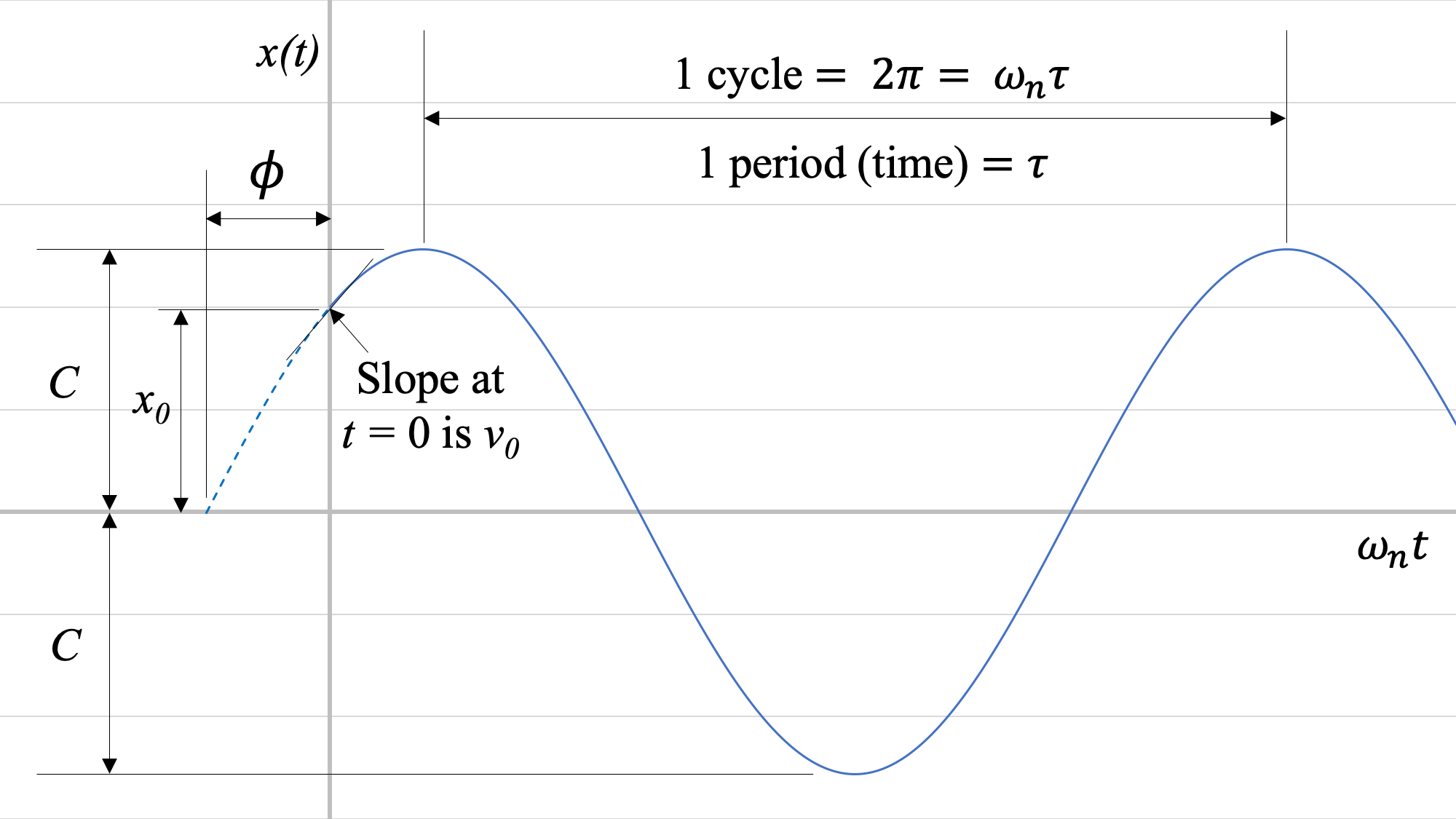
Gráfica de una función sinusoidal sobre un eje horizontal de omega_n t y un eje vertical de x (t), comenzando en t=0. La gráfica sinusoidal se ha desplazado ligeramente hacia la izquierda, por lo que existe una distancia de phi entre el eje vertical y la intersección más cercana del eje horizontal con la gráfica proyectada a la izquierda de t=0. C es la amplitud, o la distancia entre el eje horizontal y los puntos más altos o más bajos de la función sinusoidal; la pendiente de la gráfica en t=0 es v_0; y hay un ciclo de 2 unidades pi, o omega_n * tau donde tau es el periodo, entre dos máximos o mínimos adyacentes de la gráfica. — Figura\(\PageIndex{6}\): Respuesta de desplazamiento del sistema de resorte de masa (solución a la ecuación diferencial).

Para un sistema donde hay vibración torsional (es decir, la oscilación implica una rotación), las ecuaciones son de manera similar:

\[ I \ddot{\theta} + k \theta = 0 \]

\[ \Rightarrow \ddot{\theta} + \frac{k}{I} \theta = 0 \]

\[ \Rightarrow \ddot{\theta} + \omega_n^2 \theta = 0, \]

\[ \text{where} \,\, \omega_n = \sqrt{\frac{k}{I}}. \]

Suponiendo que la perturbación inicial del sistema puede describirse por la posición y velocidad de la masa en\(t=0\),

\[x(0) = x_0 \]

\[ v(0) = \dot{x}(0) = v_0. \]

La solución a la ecuación diferencial, que proporciona la posición\(x(t)\) del sistema en el momento\(t\), es:

\[ x(t) = C \sin (\omega_n t + \phi) \]

\[ \text{where:} \quad \omega_n = \sqrt{\frac{k}{I}}, \,\, C = \sqrt{ \left( \frac{\omega_0}{\omega_n} \right) ^2 + \theta_0^2 }, \,\, \phi = \tan ^{-1} \left( \frac{\theta_0 \omega_n}{\omega_0} \right). \]

Ejemplo\(\PageIndex{1}\)

Encuentra una expresión para la frecuencia natural angular del siguiente sistema, y encuentra la amplitud máxima de vibración del sistema con masa\(m\) = 10 kg y constante de resorte\(k\) = 200 N/m cuando se le da un desplazamiento inicial de\(x_0\) = 0.1 m y una velocidad inicial de\(v_0\) = 0.3 m/ s.

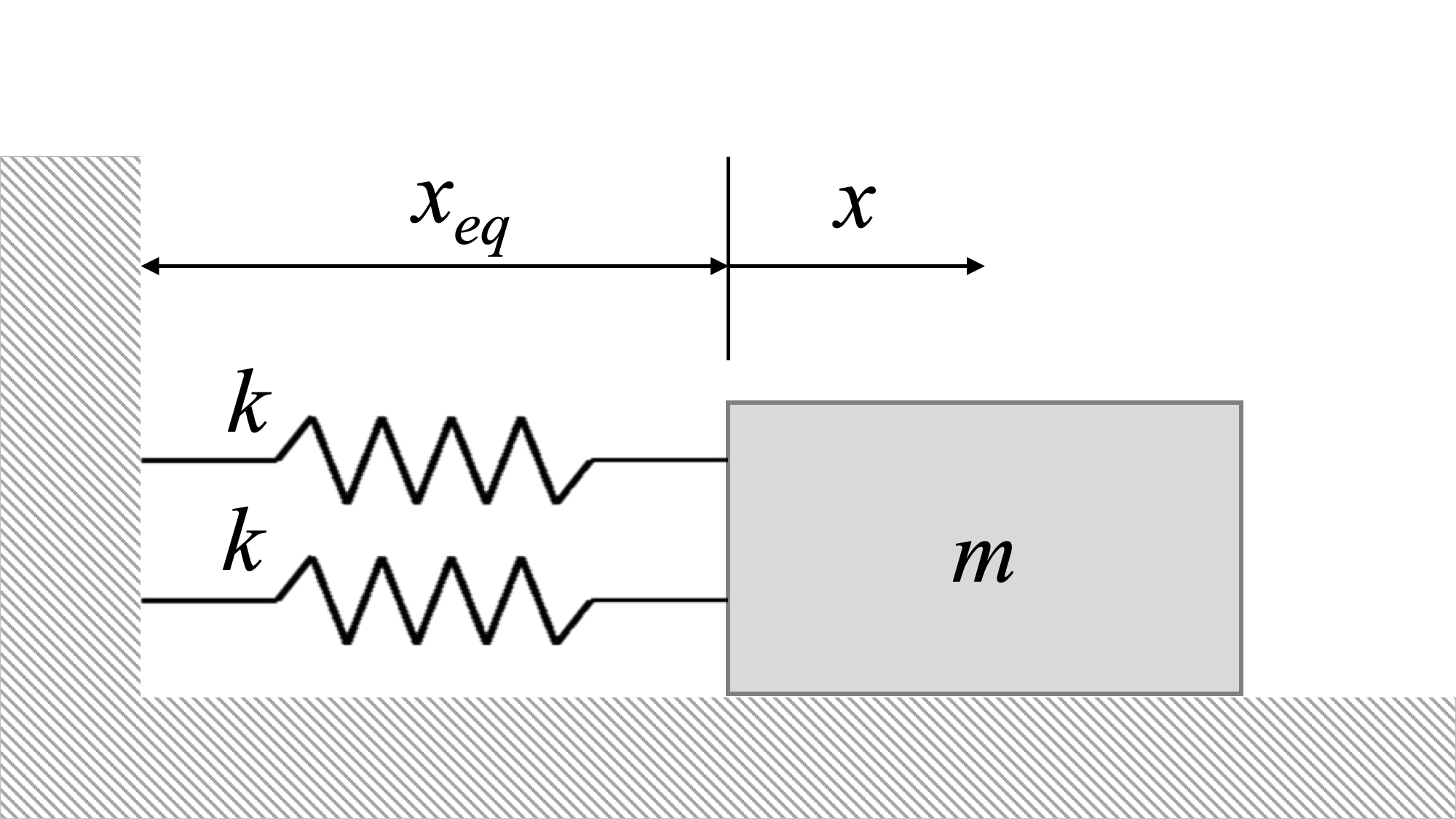
Una masa rectangular m se asienta sobre una superficie plana. El borde izquierdo de la masa está unido a los extremos derechos de dos muelles horizontales idénticos, uno encima del otro. El extremo izquierdo de cada resorte está unido a una pared. Los resortes están actualmente en su longitud de equilibrio x_eq, y la masa está en la posición x = 0 con la dirección x positiva a la derecha. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una masa rectangular sobre una superficie plana tiene su borde izquierdo unido a dos muelles idénticos, cuyos otros extremos están unidos a una pared.

Solución: Video\(\PageIndex{1}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\). Fuente de YouTube: https://youtu.be/J1TVxxVjV_c.

Ejemplo\(\PageIndex{2}\)

Determinar la ecuación de movimiento del sistema a partir de la Segunda Ley de Newton. Supongamos masa\(m\) = 5 kg y constante de resorte\(k\) = 500 N/m. Encuentre el desplazamiento inicial\(x_0\), de tal manera que la masa oscile en un rango total de 4 metros. Supongamos que la velocidad de perturbación inicial\(v_0\),, es de 10 m/s.

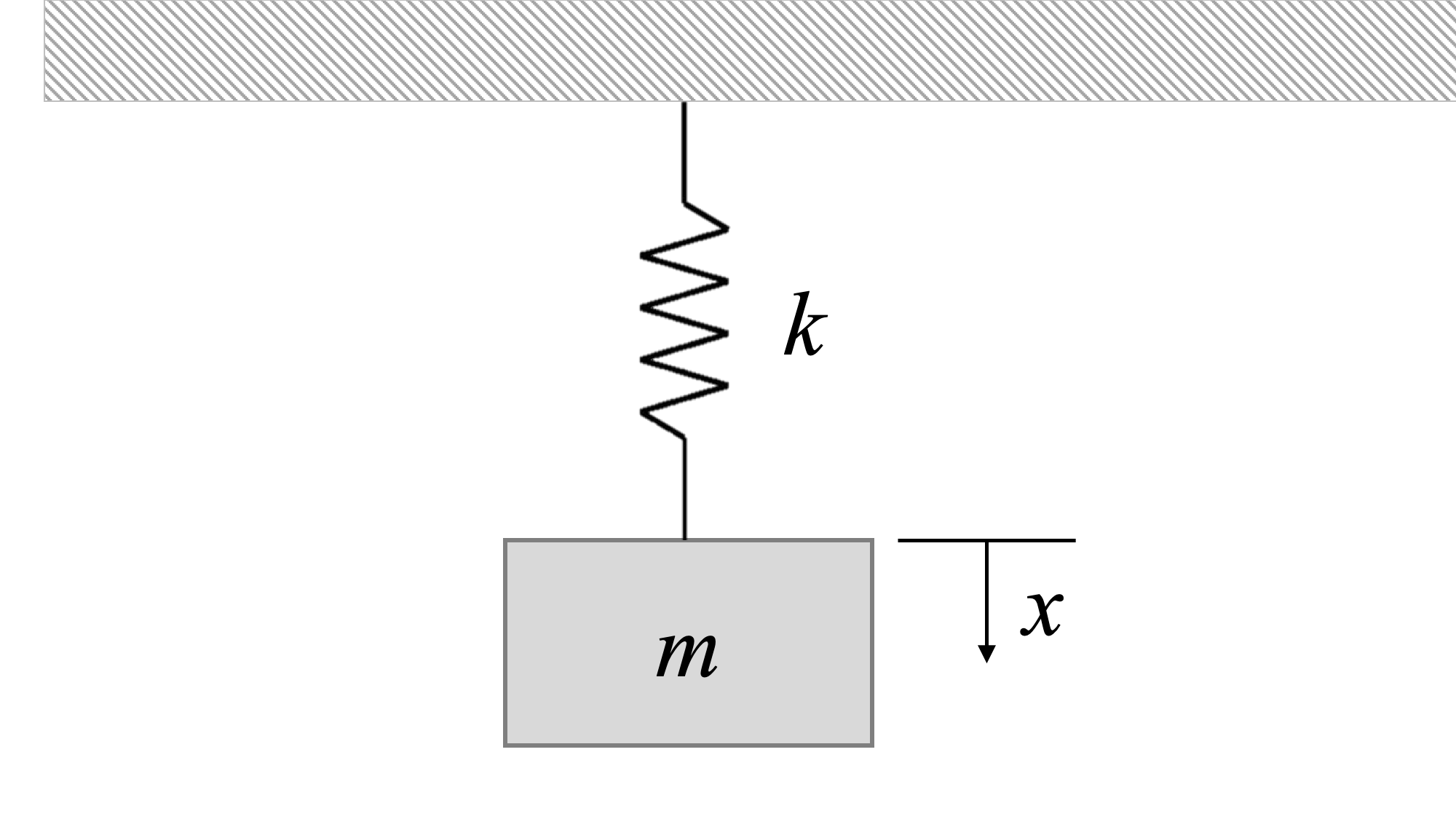
Un resorte vertical cuelga de un techo. Una masa m está unida al extremo libre del resorte, y el sistema está en reposo. La dirección x positiva apunta hacia la parte inferior de la página, siendo la posición actual de la masa x = 0. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Una masa cuelga de un resorte unido a un techo.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\). Fuente de YouTube: https://youtu.be/TAy412iVvwE.