15.2: Vibraciones libres viscosas amortiguadas

Última actualización
Guardar como PDF

Page ID: 84057

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La amortiguación viscosa es una amortiguación que es proporcional a la velocidad del sistema. Es decir, cuanto más rápido se mueve la masa, más fuerza de amortiguación resiste ese movimiento. Los fluidos como el aire o el agua generan fuerzas de arrastre viscosas.

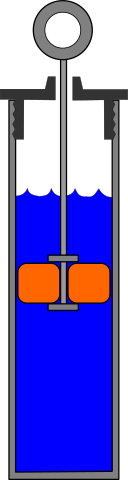
Diagrama de un amortiguador, o un amortiguador viscoso en el que el fluido en un tubo vertical a través del cual pasa un pistón resiste el movimiento hacia arriba y hacia abajo de una masa unida a ese tubo.hed a un pistón. — Figura\(\PageIndex{1}\): Diagrama que muestra el mecanismo básico en un amortiguador viscoso. A medida que el sistema (masa) unido al bucle en la parte superior vibra hacia arriba y hacia abajo, el amortiguador resistirá el movimiento en ambas direcciones debido al paso del pistón a través del fluido. Imagen de Egmason, CC-BY SA.

Solo consideraremos amortiguadores viscosos lineales, es decir donde la fuerza de amortiguación es linealmente proporcional a la velocidad. La ecuación para la fuerza o momento producido por el amortiguador, en cualquiera\(x\) o\(\theta\), es:

\[ \vec{F}_c = c \vec{\dot{x}}, \]

\[ \vec{M}_c = c \vec{\dot{\theta}}, \]

donde\(c\) esta la constante de amortiguacion. Esta es una propiedad física del amortiguador basada en el tipo de fluido, tamaño del pistón, etc. Tenga en cuenta que las unidades de\(c\) cambio dependiendo de si se trata de amortiguar el movimiento lineal (N-S/m) o el movimiento rotacional (N-m s/rad).

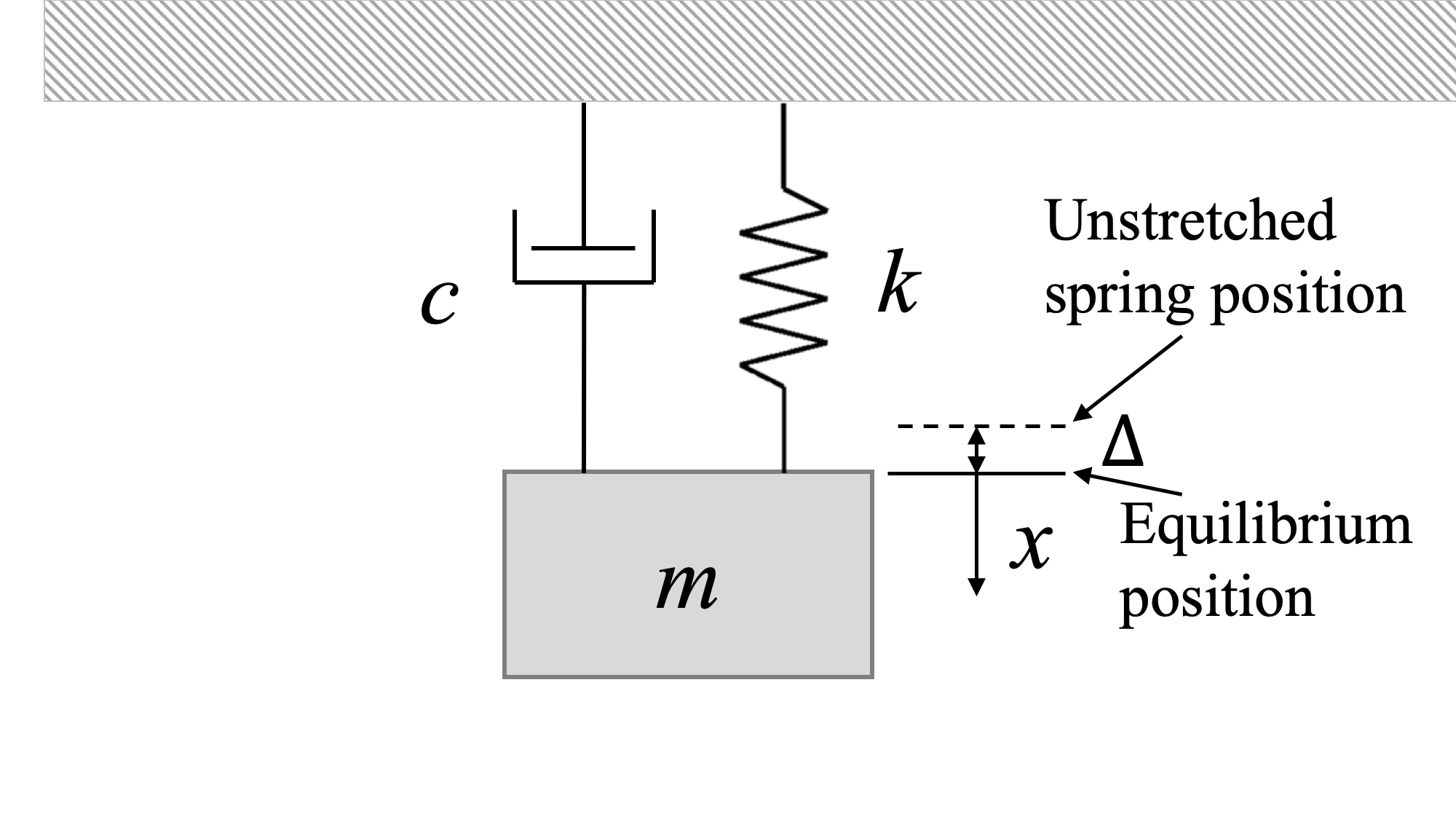
Un resorte de constante de resorte k cuelga del techo, con una masa rectangular m colgando de su extremo libre. Un amortiguador viscoso lineal de constante de amortiguación c también conecta la masa al techo. En equilibrio, la posición actual de la masa, x = 0, es una pequeña distancia Delta por debajo de la posición del resorte no estirado. La dirección x positiva apunta hacia la parte inferior de la página. — Figura\(\PageIndex{2}\): Diagrama de un sistema de masa-resorte colgante, con un amortiguador viscoso lineal, en posición de equilibrio. El resorte se estira desde su longitud natural.

Cuando el sistema está en reposo en la posición de equilibrio, el amortiguador no produjo fuerza sobre el sistema (sin velocidad), mientras que el resorte puede producir fuerza sobre el sistema, como en la masa colgante que se muestra arriba. Recordemos que esta es la posición de equilibrio, pero el resorte NO está en su longitud no estirada, ya que la masa estática produce una extensión del resorte.

Diagrama de cuerpo libre de la masa de la Figura 2 anterior. La masa experimenta una fuerza descendente de la gravedad, equilibrada por una fuerza ascendente desde el resorte. — Figura\(\PageIndex{3}\): Diagrama de cuerpo libre del sistema en posición de equilibrio. El resorte está en su posición de equilibrio, pero se estira y produce una fuerza.

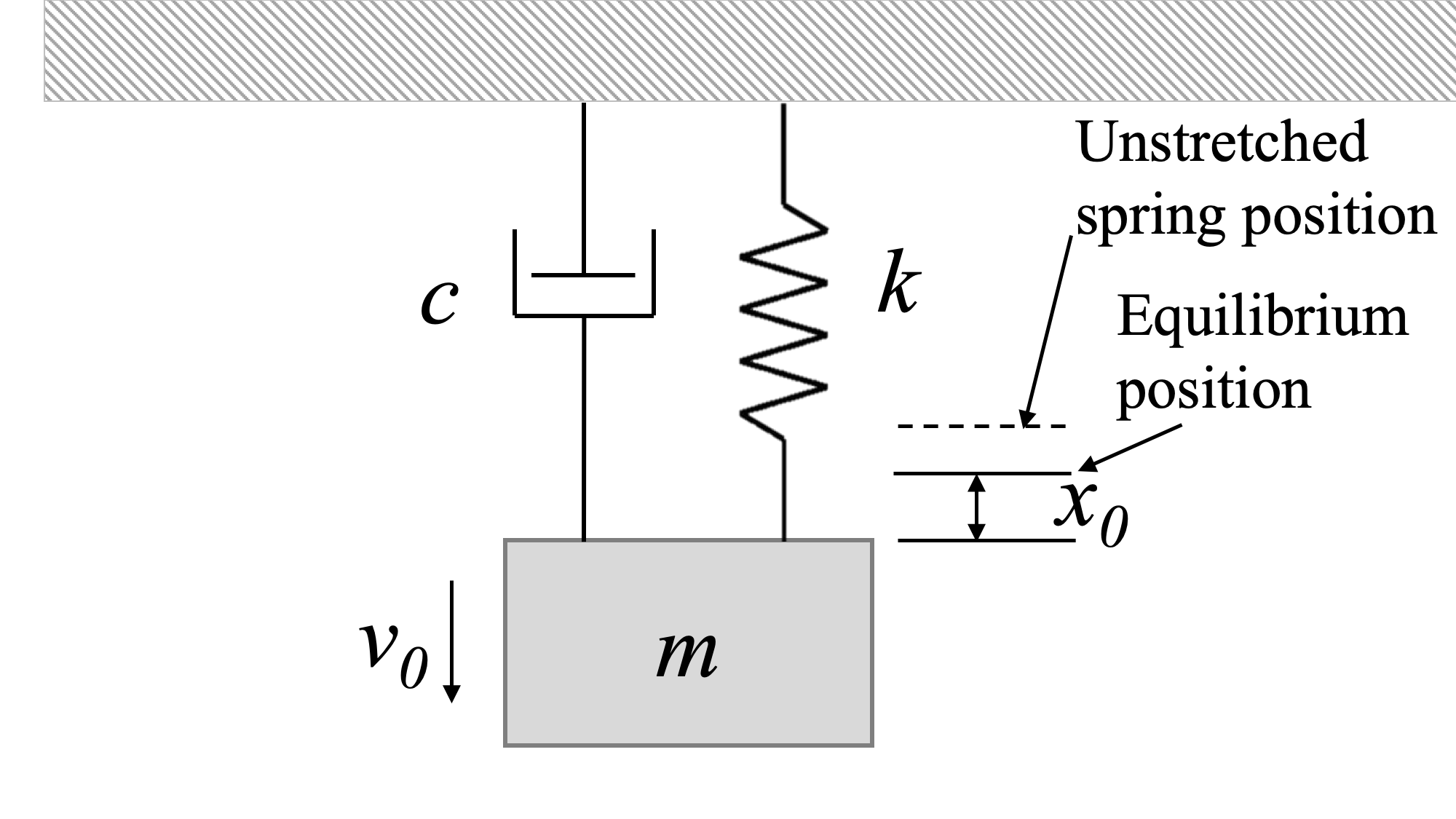
Si perturbimos el sistema (aplicando un desplazamiento inicial, una velocidad inicial, o ambos), el sistema tenderá a volver a su posición de equilibrio. El aspecto de ese movimiento dependerá de los parámetros del sistema (\(m\),\(c\), y\(k\)).

Diagrama del sistema de la Figura 2 anterior, ligeramente perturbado en la dirección x positiva. El muelle se ha estirado aún más, y el pistón en el amortiguador se ha tirado ligeramente hacia abajo, en comparación con sus posiciones de equilibrio en la figura 2. — Figura\(\PageIndex{4}\): El sistema en una posición perturbada. El resorte se estira más y el amortiguador se extiende, en comparación con sus posiciones de equilibrio.

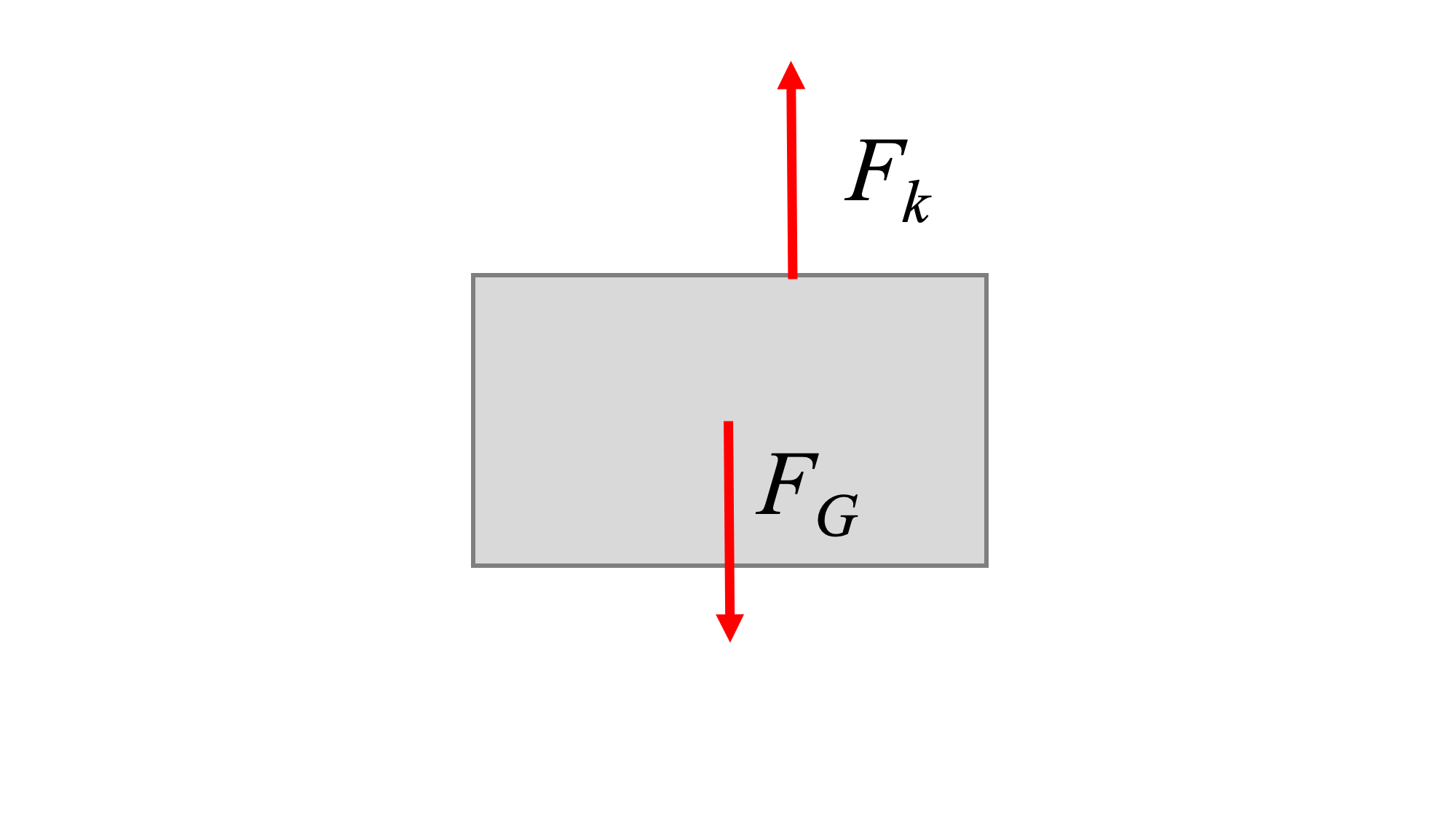
Para determinar la ecuación de movimiento del sistema, dibujamos un diagrama de cuerpo libre del sistema con perturbación y aplicamos la Segunda Ley de Newton.

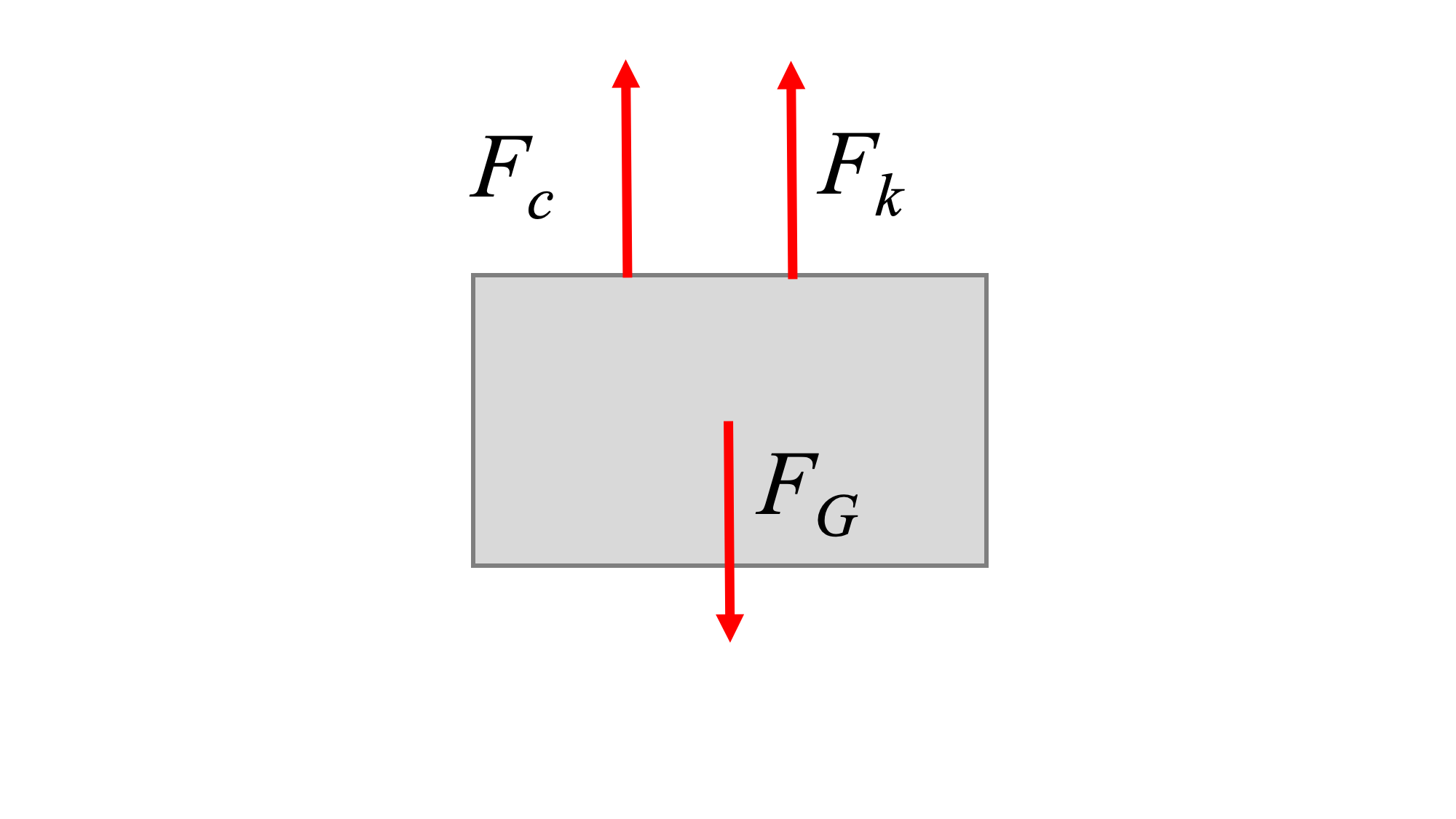
Diagrama de cuerpo libre de la masa de la Figura 4 anterior. La masa experimenta una fuerza hacia abajo de la gravedad, así como fuerzas hacia arriba desde el resorte y el amortiguador. — Figura\(\PageIndex{5}\): Diagrama de cuerpo libre del sistema con perturbación.

El proceso para encontrar la ecuación de movimiento del sistema es nuevamente:

Dibuje el sistema con una pequeña perturbación positiva (\(x\)o\(\theta\)).
Dibuja el diagrama de cuerpo libre del sistema perturbado. Asegúrese de que la fuerza del resorte y la fuerza del amortiguador tengan direcciones opuestas a la perturbación.
Encuentra la única ecuación de movimiento para el sistema en la coordenada perturbada usando la Segunda Ley de Newton. Mantenga la misma dirección positiva para la posición y asigne aceleración positiva en la misma dirección.
Mueva todos los términos de la ecuación a un lado y verifique que todos los términos sean positivos. Si todos los términos no son positivos, hay un error en la dirección de desplazamiento, aceleración y/o fuerza del resorte o amortiguador.

Para el sistema de ejemplo anterior, con masa\(m\), constante de resorte\(k\) y constante de amortiguación\(c\), derivamos lo siguiente:

\[ \sum F_x = m a_x = m \ddot{x} \]

\[ -F_k - F_c = m \ddot{x} \]

\[ -kx - \dot{c(x)} = m \ddot{x} \]

\[ m \ddot{x} + \dot{c(x)} + kx = 0 \]

Esto nos da una ecuación diferencial que describe el movimiento del sistema. Podemos reescribirlo en forma normal:

\[ m \ddot{x} + c \dot{x} + kx = 0 \]

\[ \Rightarrow \ddot{x} + \frac{c}{m} \dot{x} + \frac{k}{m} x = 0 \]

\[ \Rightarrow \ddot{x} + 2 \zeta \omega_n \dot{x} + \omega_n^2 x = 0 \]

Como antes, al término\(\omega_n\) se le llama la frecuencia natural angular del sistema, y tiene unidades de rad/s.

\[ \omega_n ^2 = \frac{k}{m}\, ; \quad \omega_n = \sqrt{\frac{k}{m}} \]

\(\zeta\)(zeta) se llama la relación de amortiguación. Se trata de un término adimensional que indica el nivel de amortiguación, y por tanto el tipo de movimiento del sistema amortiguado.

\[ \zeta = \frac{c}{c_c} = \frac{\text{actual damping}}{\text{critical damping}} \]

La expresión para amortiguación crítica proviene de la solución de la ecuación diferencial. La solución a la ecuación diferencial del sistema es de la forma

\[ x(t) = a e^{rt}, \]

donde\(a\) es constante y el valor o valores de\(r\) pueden ser pueden obtenerse diferenciando esta forma general de la solución y sustituyéndola en la ecuación de movimiento.

\[ m r^2 e^{rt} + c r e^{rt} + k e^{rt} = 0 \]

\[ \Rightarrow (mr^2 + cr + k) e^{rt} = 0 \]

Debido a que el término exponencial nunca es cero, podemos dividir ambos lados por ese término y obtener:

\[ m r^2 + cr + k = 0. \]

Usando la fórmula cuadrática, podemos encontrar las raíces de la ecuación:

\[ r_{1,2} = \frac{-c \pm \sqrt{c^2 - 4mk}}{2m} \]

La amortiguación crítica ocurre cuando el término bajo el signo de raíz cuadrada es igual a cero:

\[ c_c ^2 = 4 mk \]

\[ c_c = 2 \sqrt{mk} = 2 m \omega_n \]

Cuatro estuches viscosos de amortiguación:

Hay cuatro casos básicos para la relación de amortiguación. Para las soluciones que siguen en cada caso, asumiremos que el desplazamiento de perturbación inicial del sistema es\(x_0\) y la velocidad de perturbación inicial del sistema es\(v_0\).

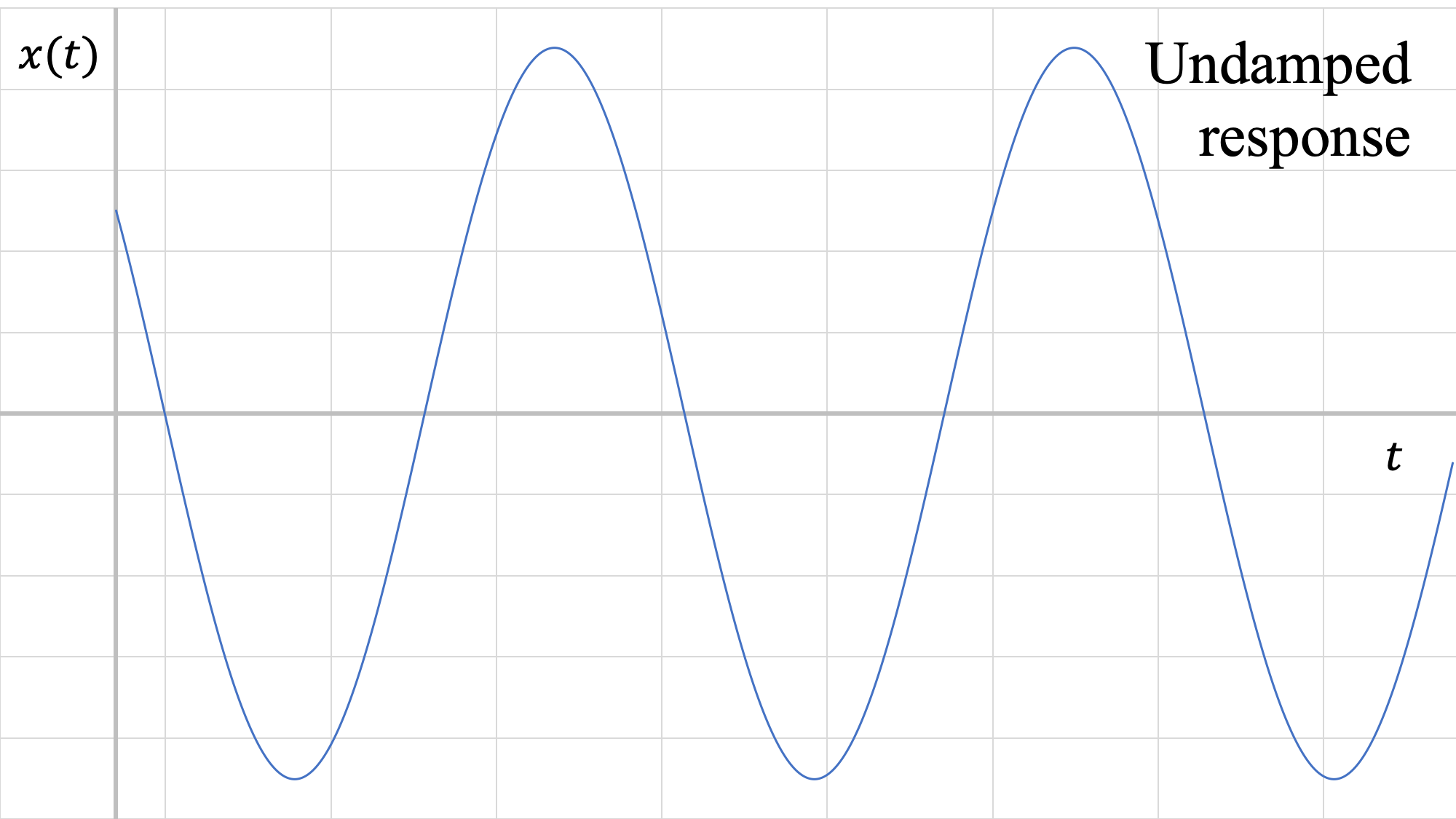
1. \(\zeta = 0\): Sin amortiguar

\[ c = 0 \]

Este es el caso cubierto en el apartado anterior. Los sistemas no amortiguados oscilan continuamente alrededor de la posición de equilibrio, a menos que se aplique alguna otra fuerza.

Gráfica de posición (x (t)) vs tiempo (t). Graph toma la forma de una gráfica sinusoidal desplazada horizontalmente de manera que x (0) es igual a algún valor positivo en lugar de 0. — Figura\(\PageIndex{6}\): Respuesta de un sistema sin amortiguar.

2. \(\zeta > 1\): Sobrehumedecido

\[ c^2 > 4 mk \]

Las raíces son tanto reales como negativas, pero no iguales entre sí. Los sistemas sobreamortiguados se mueven lentamente hacia el equilibrio sin oscilar.

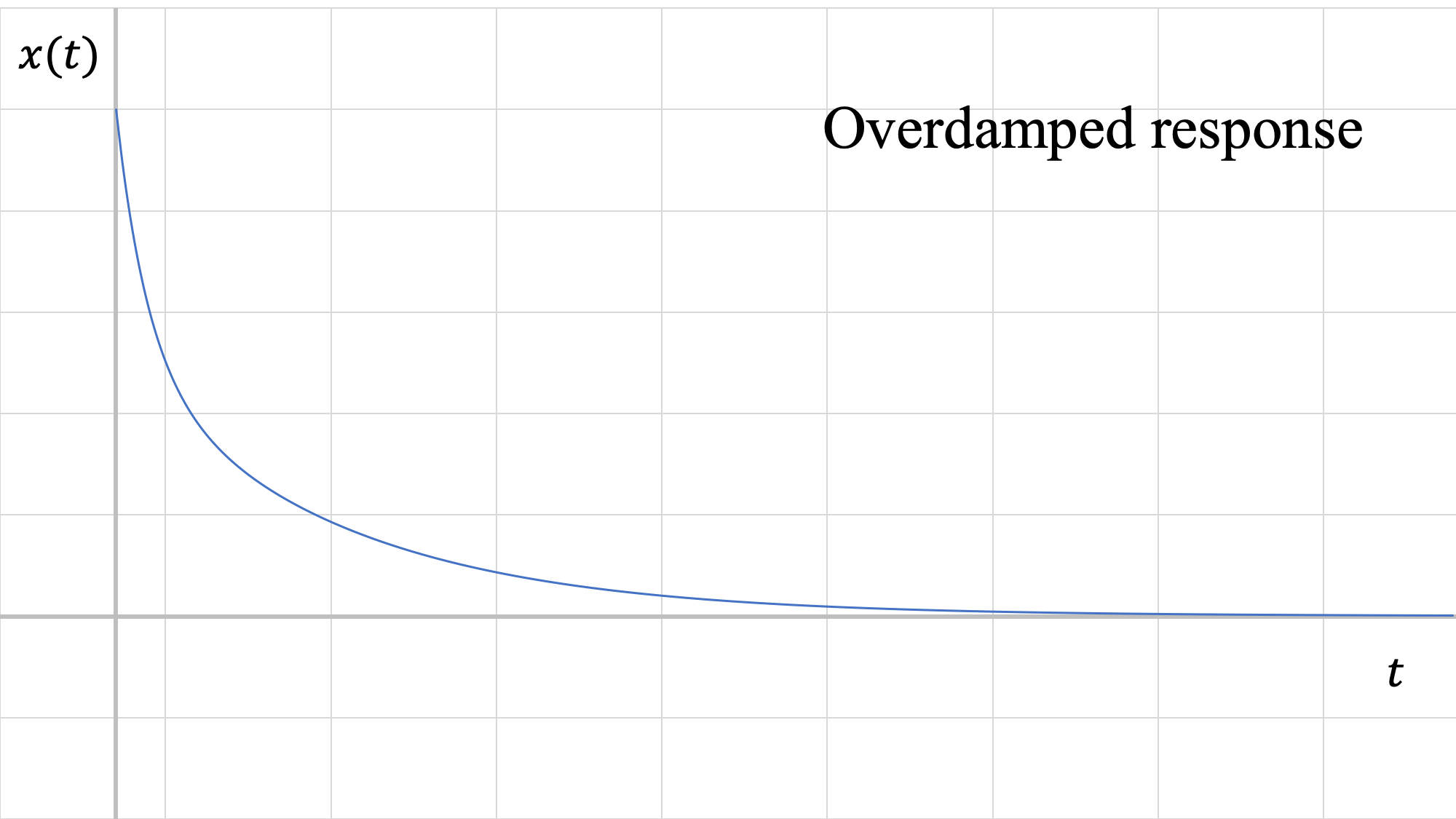
Una gráfica de respuesta del sistema sobreamortiguada, que toma la forma de una gráfica de decaimiento exponencial, en el primer cuadrante de una gráfica de ejes x (t) vs t. — Figura\(\PageIndex{7}\): Respuesta de un sistema sobreamortiguado.

La respuesta para un sistema sobreamortiguado es:

\[ x(t) = a_1 e^{ \left( \frac{-c + \sqrt{c^2 - 4mk}}{2m} \right) t} + a_2 e^{ \left( \frac{-c - \sqrt{c^2 - 4mk}}{2m} \right) t}, \]

\[ \text{where} \,\, a_1 = \frac{-v_0 + r_2 x_0}{r_2 - r_1} \,\, \text{and} \,\, a_2 = \frac{v_0 + r_1 x_0}{r_2 - r_1}. \]

3. \(\zeta = 1\): Amortiguado críticamente

\[ c^2 = 4 mk ( = c_c^2) \]

Las raíces son reales y ambas iguales a\(- \omega_n\). Los sistemas amortiguados críticamente permitirán el retorno más rápido al equilibrio sin oscilación.

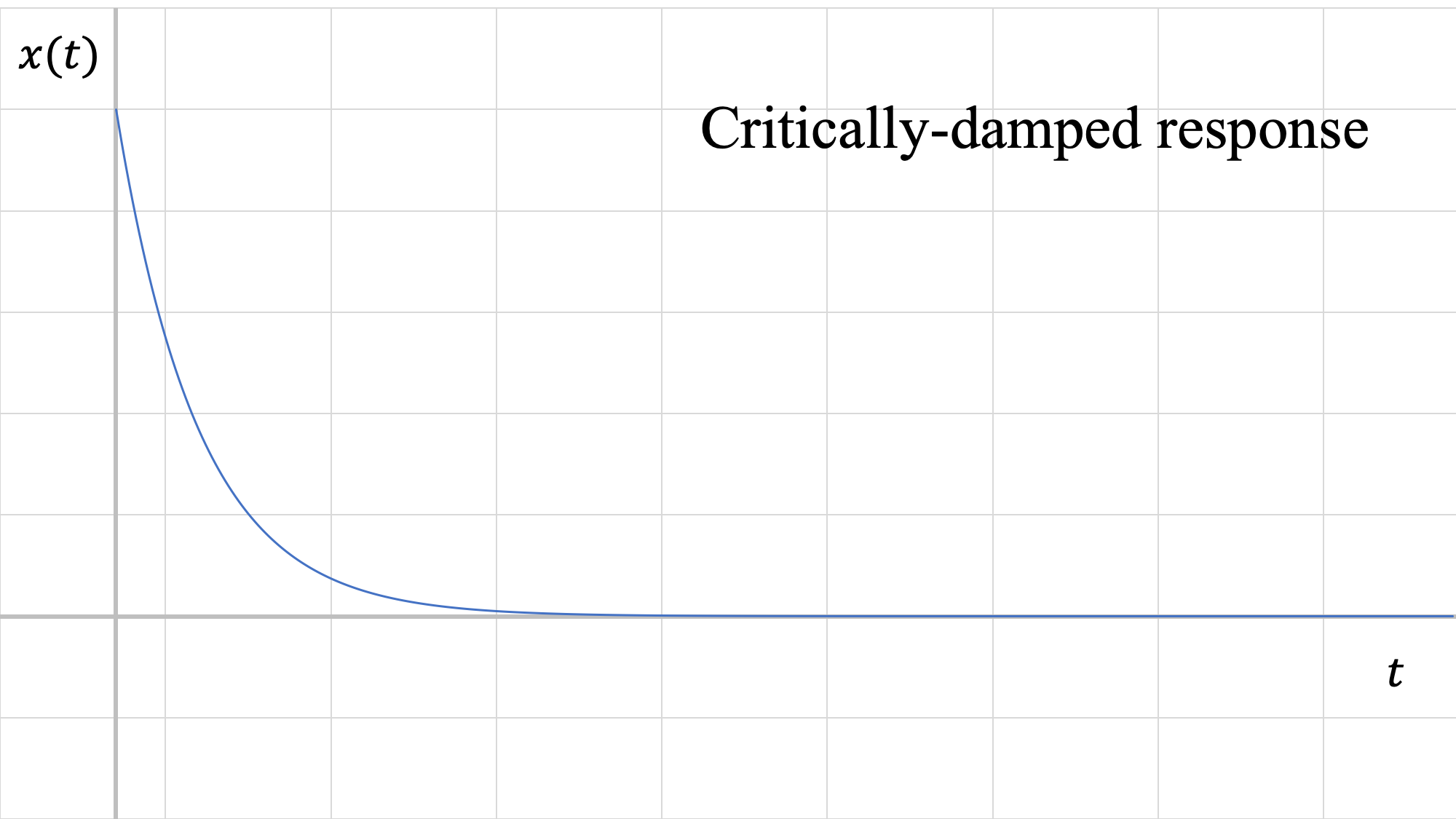
Una gráfica de respuesta del sistema amortiguada críticamente, en el primer cuadrante de una gráfica con ejes x (t) vs t. La gráfica toma la forma de una gráfica de decaimiento exponencial, que se aproxima a cero mucho más rápidamente que la gráfica de la respuesta sobreamortiguada en la Figura 7 anterior. — Figura\(\PageIndex{8}\): Respuesta de un sistema amortiguado críticamente.

La solución para un sistema amortiguado críticamente es:

\[ x(t) = (A + Bt) e^{-\omega_n t} , \]

\[ \text{where} \,\, A = x_0 \,\, \text{and} \,\, B = v_0 + x_0 \omega_n. \]

4. \(\zeta < 1\): Subamortiguado

\[ c^2 < 4 mk \]

Las raíces son números complejos. Los sistemas subamortiguados oscilan alrededor del punto de equilibrio; a diferencia de los sistemas no amortiguados, la amplitud de las oscilaciones disminuye hasta que el sistema finalmente deja de moverse en la posición de equilibrio.

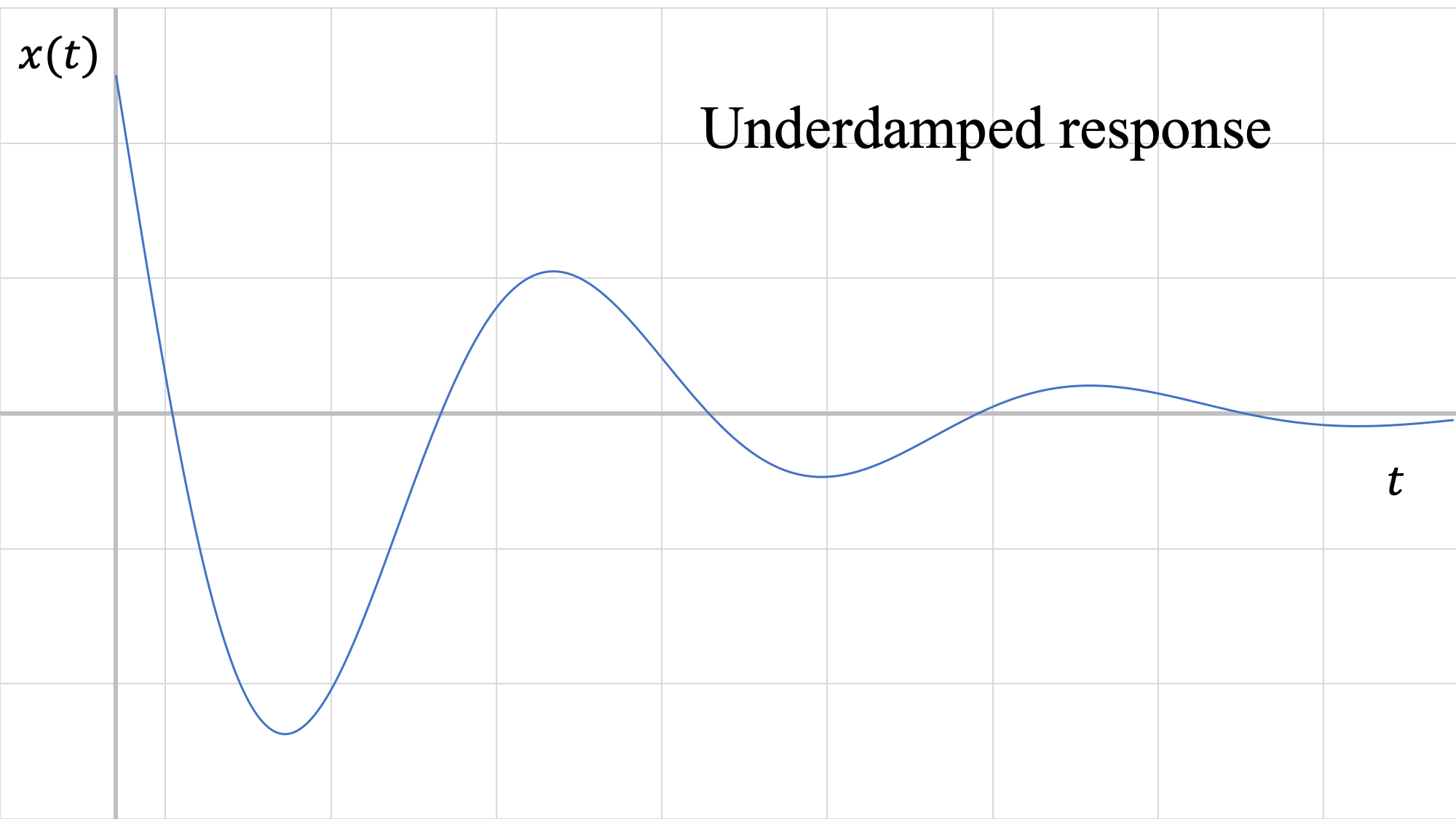
Gráfica de una respuesta de sistema subamortiguada, en una gráfica con ejes x (t) vs t. A t = 0 la gráfica comienza en un valor x (t) positivo, y oscila alrededor del eje t horizontal con una amplitud menor en cada oscilación sucesiva. — Figura\(\PageIndex{9}\): Respuesta de un sistema de amortiguación insuficiente.

La solución para un sistema de amortiguación insuficiente es:

\[ x(t) = [ C_1 \sin (\omega_d t) + C_2 \cos (\omega_d t) ] e^{- \omega_n \zeta t} , \]

\[ \text{where} \,\, C_1 = \frac{v_0 + \omega_n \zeta x_0}{\omega_d}, \,\, C_2 = x_0, \,\, \text{and} \,\, \zeta = \frac{c}{2 m \omega_n}. \]

\(\omega_d\)se llama la frecuencia natural amortiguada del sistema. Siempre es menor que\(\omega_n\):

\[ \omega_d = \omega_n \sqrt{1 - \zeta^2}. \]

El período de la respuesta subamortiguada también difiere de la respuesta no amortiguada.

\[ \text{Undamped:} \quad \tau_n = \frac{2 \pi}{\omega_n} \]

\[ \text{Underdamped:} \quad \tau_d = \frac{2 \pi}{\omega_d} \]

Comparación de Estuches de Amortiguación Viscosa:

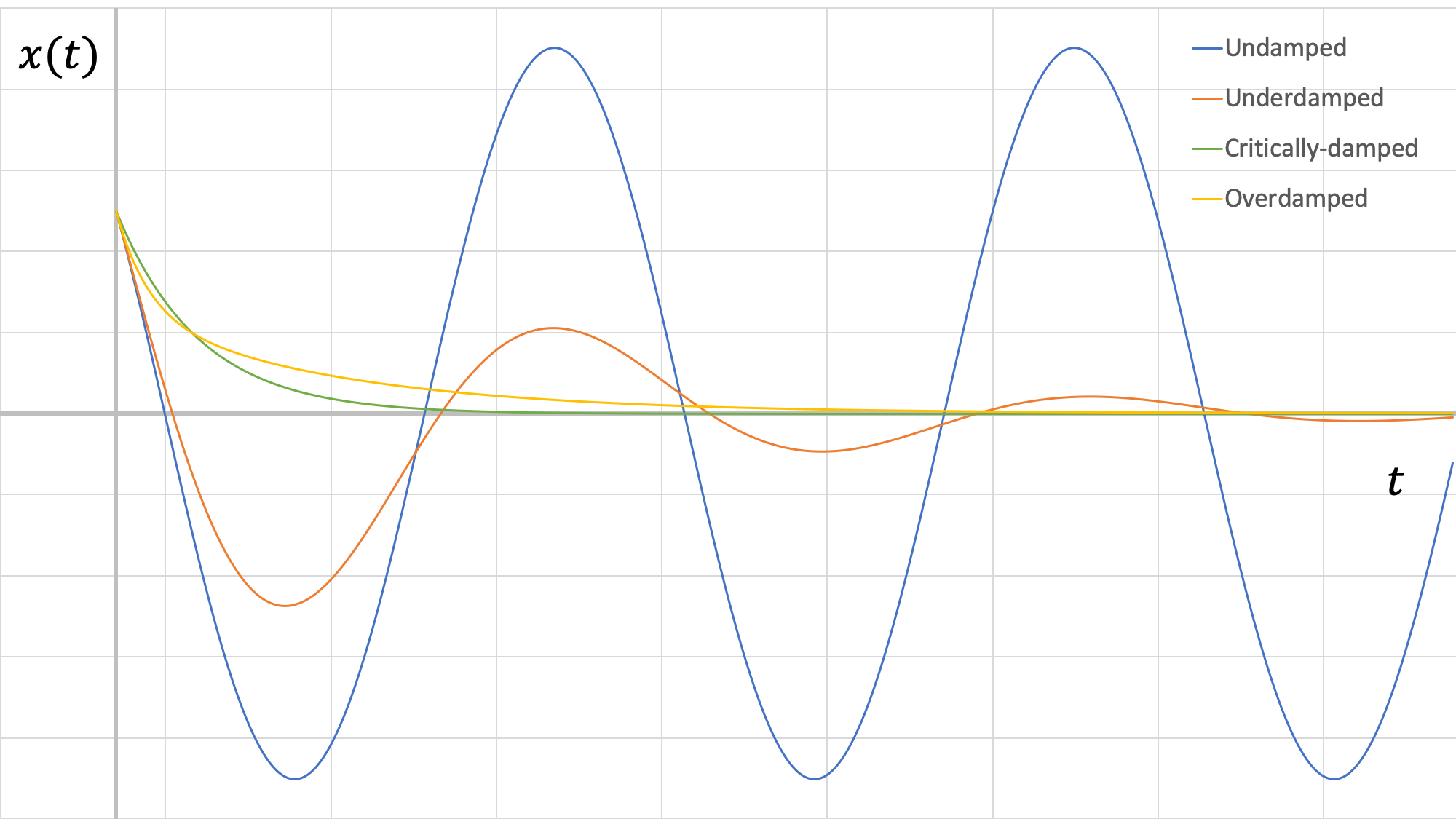
Gráfica comparando los cuatro tipos diferentes de respuestas de amortiguación del sistema. Todas las gráficas se muestran en el mismo conjunto de ejes, con t como eje horizontal y x (t) como vertical. Todas las gráficas comienzan con el mismo valor positivo de x (t) a t = 0. El sistema sin amortiguar, mostrado en azul, oscila alrededor del eje t con amplitud consistente. El sistema subamortiguado, mostrado en rojo, oscila alrededor del eje t con una amplitud decreciente a lo largo del tiempo. El sistema amortiguado críticamente, mostrado en verde, sufre una rápida descomposición exponencial. El sistema sobreamortiguado, mostrado en amarillo, sufre una decadencia exponencial más gradual. — Figura\(\PageIndex{10}\): Respuestas para los cuatro tipos de sistema (o valores de relación de amortiguación) en amortiguamiento viscoso. Los cuatro sistemas tienen los mismos valores de masa y resorte, y se les han dado las mismas perturbaciones iniciales (posición inicial y velocidad inicial); esto es evidente porque comienzan en la misma\(y\) intercepción y tienen la misma pendiente en\(x=0\).

En la figura anterior, podemos ver que la respuesta críticamente amortiguada da como resultado que el sistema vuelva al equilibrio más rápido. Además, podemos ver que la amplitud del sistema subamortiguado está bastante atenuada en comparación con la caja no amortiguada.