17.1: Integrales de momento
- Page ID
- 84020
Un momento integral, como su nombre lo indica, es el concepto general de utilizar la integración para determinar el momento neto de una fuerza que se extiende sobre un área o volumen. Debido a que los momentos son generalmente una fuerza veces una distancia, y debido a que las fuerzas distribuidas se extienden en un rango de distancias, necesitaremos usar cálculo para determinar el momento neto ejercido por una fuerza distribuida.
\[ \int M = \int F(d) * d \]
Más allá de la definición más literal de un momento integral, el término “momento integral” también es general aplicado al proceso de integración de áreas distribuidas o masas que estarán resistiendo algún momento alrededor de un eje establecido.
Algunas de las aplicaciones de las integrales de momento incluyen:
- Encontrar cargas puntuales que sean equivalentes a cargas distribuidas (la carga puntual equivalente).
- Encontrar el centroide (centro geométrico) o centro de masa para formas 2D y 3D.
- Encontrar el momento de inercia del área para una sección transversal de viga, que será un factor en la resistencia de esa viga a la flexión.
- Encontrar el momento de inercia del área polar para una sección transversal del eje, que será un factor en la resistencia de ese eje a la torsión.
- Encontrar el momento de inercia de masa, indicando la resistencia de un cuerpo a las aceleraciones angulares.
Al mirar integrales de momento, hay un número de diferentes tipos de integrales de momento. Estas incluirán integrales de momento en una dimensión, dos dimensiones y tres dimensiones; integrales de momento de funciones de fuerza, de áreas/volúmenes o de distribuciones de masa; integrales de momento de primer orden o segundo orden; e integrales de momento rectangulares o polares.
Cualquier combinación de estos diferentes tipos es posible (por ejemplo, una integral de momento de área 2D rectangular de primer orden o una integral de momento de masa polar 3D de segundo orden). Sin embargo, sólo algunas de estas combinaciones tendrán aplicaciones prácticas y serán discutidas en detalle en páginas futuras.
Integrales de Momento 1D, 2D y 3D
Técnicamente podemos tomar el momento integral en cualquier número de dimensiones, pero para fines prácticos nunca trataremos con integrales de momento más allá de tres dimensiones. El número de dimensiones afectará la complejidad de los cálculos (siendo las integrales de momento tridimensionales más involucradas que las integrales de momento unidimensionales o bidimensionales), pero la naturaleza del problema dictará las dimensiones necesarias. A menudo esto no aparece listado en el tipo de momento integral, requiriendo que asuma el tipo en función del contexto del problema.
Integrales de Fuerza, Área/Volumen y Momento Masivo
La siguiente distinción en integrales de momento se hace con respecto a lo que estamos integrando. Generalmente, podemos integrar funciones de fuerza en cierta distancia, área o volumen, podemos integrar la función de área o volumen en sí, o podemos integrar la distribución de masa sobre el área o volumen. Cada uno de estos tipos de integrales de momento tiene un propósito diferente y comenzará con una función matemática diferente para integrar, pero el proceso de integración más allá de eso será muy similar.
Integrales de primer momento vs segundo
Para integrales de momento siempre estaremos multiplicando la función de fuerza, la función de área o volumen, o la función de distribución de masa por una distancia o una distancia al cuadrado. Las integrales del primer momento simplemente multiplican la función inicial por la distancia, mientras que las integrales del segundo momento multiplican la función por la distancia al cuadrado. Nuevamente, el tipo de integral de momento que usaremos depende de nuestra aplicación, con cosas como carga puntual equivalente, centroides y centro de masa que dependen de integrales de primer momento, y momentos de inercia de área, momentos polares de inercia y momentos de inercia de masa basados en integrales de segundo momento. Como probablemente puedas deducir de esta lista, las integrales de segundo momento, suelen ser etiquetadas como un momento de inercia.
Integrales Rectangulares vs Momento Polar
Finalmente hablaremos de integrales de momento rectangulares versus integrales de momento polar. Esta es una diferencia en cómo definimos la distancia en nuestro momento integral. Empecemos por la distinción en 2D. Si nuestra distancia se mide desde algún eje (por ejemplo, el\(x\) eje -eje, o el\(y\) -eje) entonces es una integral de momento rectangular. Por otro lado, si la distancia se mide desde algún punto (como el origen), entonces es una integral de momento polar.
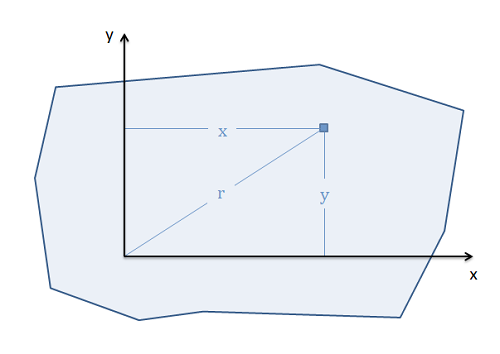
Esta distinción es importante para cómo tomaremos la integral. Para integrales de momento rectangulares nos moveremos de izquierda a derecha o de abajo hacia arriba. Para integrales de momento polar tomaremos la integral irradiando desde el punto central.
En los problemas tridimensionales, las definiciones cambian ligeramente. Para integrales de momento rectangulares, la distancia se medirá desde algún plano (como el\(xy\) -plano,\(xz\) -plano o\(yz\) -plano). Nuevamente integraremos de izquierda a derecha, de abajo a arriba, o ahora de atrás a frente con distancias correspondientes a la\(x\),\(y\) o\(z\) coordenadas de ese punto. Para una integral de momento polar, la distancia se medirá desde algún eje (como el\(x\),\(y\), o\(z\) eje), y nos integraremos irradiando hacia afuera desde ese eje.


