17.2: Centroides de Áreas vía Integración

Última actualización
Guardar como PDF

Page ID: 84014

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El centroide de un área puede ser considerado como el centro geométrico de esa área. La ubicación del centroide a menudo se denota con a\(C\) con las coordenadas siendo\((\bar{x}\),\(\bar{y})\), denotando que son la media\(x\) y\(y\) coordenada para el área. Si un área se representara como una placa delgada y uniforme, entonces el centroide sería el mismo que el centro de masa para esta placa delgada.

El centroide de un semicírculo de radio r es 4r/ (3 pi) desde el punto medio del lado recto, a lo largo del radio perpendicular a ese lado. El centroide de un triángulo rectángulo cuyas patas tienen longitudes h y b se ubica a una distancia de h/3 en la dirección de h y una distancia de b/3 en la dirección de b, con ambas distancias medidas desde el ángulo recto. El centroide de un rectángulo con longitudes laterales de b y h se ubica en la intersección de los puntos medios de lados opuestos. — Figura\(\PageIndex{1}\): El centroide (marcado\(C\)) para algunas formas comunes.

Los centroides de áreas son útiles para una serie de situaciones en la secuencia del curso de mecánica, incluyendo en el análisis de fuerzas distribuidas, la flexión en vigas y la torsión en ejes, y como un paso intermedio en la determinación de momentos de inercia.

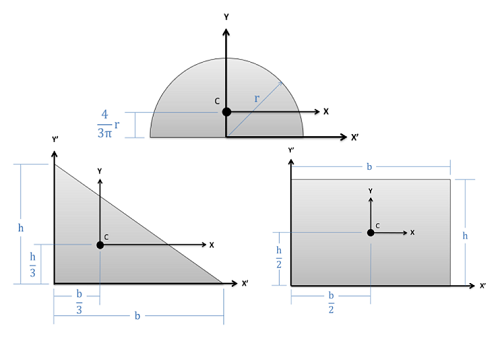
La ubicación de los centroides para una variedad de formas comunes se puede buscar simplemente en tablas, como esta tabla [1] para centroides 2D y esta tabla para centroides 3D. Sin embargo, a menudo necesitaremos determinar el centroide de otras formas; para ello, generalmente usaremos uno de dos métodos.

Podemos usar el primer momento integral para determinar la ubicación del centroide.
Podemos usar el método de piezas compuestas junto con tablas centroides para determinar la ubicación del centroide.

En esta página solo discutiremos el primer método, ya que el método de las piezas compuestas se discute en una sección posterior. Las tablas utilizadas en el método de piezas compuestas, sin embargo, se derivan a través de la integral de primer momento, por lo que ambos métodos finalmente se basan en integrales de primer momento.

Encontrar el centroide a través de la Integral de Primer Momento

Cuando encontremos el centroide de una forma bidimensional, estaremos buscando tanto una\(x\)\(y\) coordenada como una, representadas como\(\bar{x}\) y\(\bar{y}\) respectivamente. Colectivamente, esta\((\bar{x}, \bar{y}\) coordenada es el centroide de la forma.

Para encontrar la\(x\) coordenada promedio de una forma (\(\bar{x}\)), esencialmente partiremos la forma en un gran número de áreas muy pequeñas y de igual tamaño, y encontraremos la\(x\) coordenada promedio de estas áreas. Para hacer esta suma de un número infinito de cosas muy pequeñas, usaremos la integración. Específicamente, tomaremos el primer momento de área rectangular integral a lo largo del\(x\) eje, y luego dividiremos esa integral por el área total para encontrar la coordenada promedio. Podemos hacer algo similar a lo largo del\(y\) eje -para encontrar nuestro\(\bar{y}\) valor. Escribiendo todo esto, tenemos las ecuaciones a continuación.

\[ C = ( \bar{x}, \bar{y}) \]

\ begin {align}\ bar {x} &=\ dfrac {\ displaystyle\ int_ {A} (da*x)} {A}\\ [4pt]\ bar {y} &=\ dfrac {\ displaystyle\ int_ {A} (Da*y)} {A}\ end {align}

A continuación vamos a discutir qué\(dA\) representa la variable y cómo la integramos sobre el área. La variable\(dA\) es la tasa de cambio en el área a medida que nos movemos en una dirección particular. Porque\(\bar{x}\) vamos a estar moviéndonos a lo largo del\(x\) eje -eje, y para\(\bar{y}\) nos estaremos moviendo a lo largo del\(y\) -eje en estas integrales.

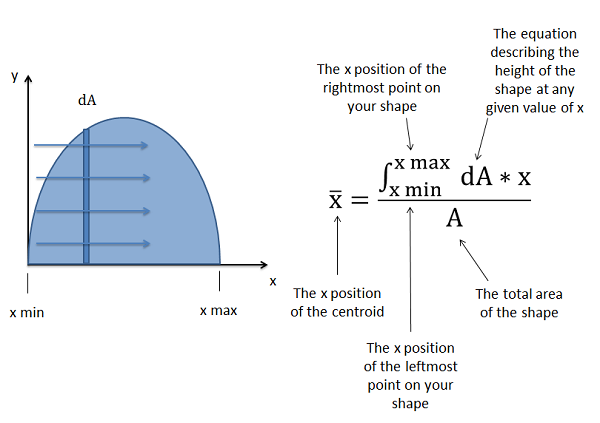
A medida que nos movemos a lo largo del\(x\) eje -eje de una forma desde su punto más a la izquierda hasta su punto más a la derecha, la velocidad de cambio del área en cualquier instante en el tiempo será igual a la altura de la forma ese punto multiplicado por la velocidad a la que nos movemos a lo largo del eje (\(dx\)). Debido a que la altura de la forma cambiará con la posición, no usamos ningún valor, sino que debemos llegar a una ecuación que describa la altura en cualquier valor dado de x. Luego multiplicaremos esta\(dA\) ecuación por la variable\(x\) (para que sea un momento integral), e integraremos eso desde la\(x\) posición más a la izquierda de la forma (\(x_{min}\)) hasta la\(x\) posición más a la derecha de la forma (\(x_{max}\)).

Una porción de una parábola que se abre hacia abajo, que contiene el vértice, se encuentra en el primer cuadrante del plano de coordenadas cartesianas. La forma está delimitada por debajo por el eje x e interseca el origen en su punto más a la izquierda, que está etiquetado como x_max. El punto más a la derecha de la forma, que también toca el eje x, está etiquetado como x_min. La forma se divide en muchas tiras verticales delgadas, cada una de las cuales se aproxima a un rectángulo delgado con un área de dA. La coordenada x del centroide es la integral de dA * x, evaluada de x_min a x_max, el conjunto dividido por el área total de la forma. — Figura\(\PageIndex{2}\): El procedimiento para calcular la\(x\) coordenada del centroide.

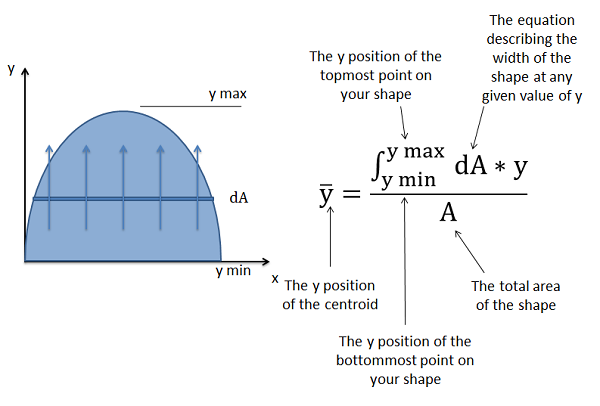
Para encontrar la\(y\) coordenada del del centroide, tenemos un proceso similar, pero debido a que nos estamos moviendo a lo largo del\(y\) eje -eje, el valor\(dA\) es la ecuación que describe el ancho de la forma multiplicado por la velocidad a la que nos estamos moviendo a lo largo del\(y\) eje (\(dy\)). Luego tomamos esta\(dA\) ecuación y la multiplicamos por\(y\) para que sea un momento integral. Integraremos esta ecuación desde la\(y\) posición del punto más bajo en la forma (\(y_{min}\)) hasta la\(y\) posición del punto más alto en la forma (\(y_{max}\)).

Usando la integral de primer momento y las ecuaciones mostradas anteriormente, teóricamente podemos encontrar el centroide de cualquier forma siempre y cuando podamos escribir ecuaciones para describir la altura y el ancho en cualquier\(y\) valor\(x\) o valor respectivamente. Para formas más complejas, sin embargo, determinar estas ecuaciones y luego integrar estas ecuaciones puede llegar a ser muy lento. Es por eso que la mayoría de las veces, los ingenieros utilizarán en su lugar el método de piezas compuestas o herramientas informáticas.

Uso de la simetría como acceso directo

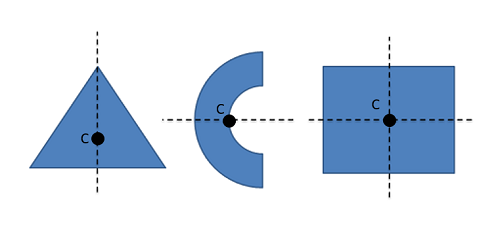
La simetría de forma puede proporcionar un atajo en muchos cálculos de centroides. Recuerda que el centroide se ubica en la media\(x\) y\(y\) coordina para todos los puntos de la forma. Si la forma tiene una línea de simetría, eso significa que cada punto en un lado de la línea debe tener un punto equivalente en el otro lado de la línea. Esto significa que el valor promedio (también conocido como el centroide) debe estar a lo largo de cualquier eje de simetría. Si la forma tiene más de un eje de simetría, entonces el centroide debe existir en la intersección de los dos ejes de simetría.

Un triángulo isósceles tiene su centroide ubicado en algún lugar de la línea de simetría que divide su base por la mitad. Un semicírculo con un semicírculo concéntrico más pequeño eliminado, produciendo una forma de C, tiene su centroide ubicado en algún lugar de la línea horizontal de simetría de la C. Un rectángulo tiene su centroide ubicado en la intersección su vertical y sus líneas horizontales de simetría. — Figura\(\PageIndex{4}\): Si una forma tiene una línea de simetría, el centroide debe estar en algún lugar a lo largo de esa línea. Si una forma tiene más de una línea de simetría, el centroide debe existir en la intersección de estas líneas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/ilgYN8c1HUk.

Ejemplo\(\PageIndex{1}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

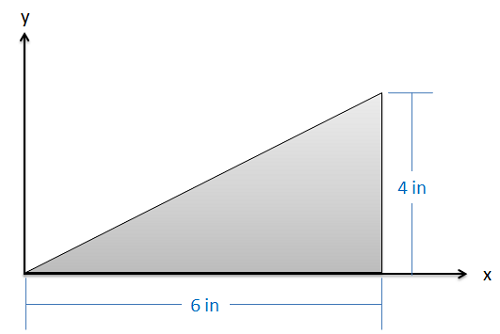
Un triángulo rectángulo se encuentra en el primer cuadrante de un plano de coordenadas cartesianas estándar. Una pata, de 6 pulgadas de largo, tiene su punto final izquierdo localizado en el origen y se encuentra a lo largo del eje x positivo. El segundo tramo, de 4 pulgadas de largo, se extiende hacia arriba desde el punto final derecho de la pata horizontal. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un triángulo rectángulo con una pata tendida a lo largo del\(x\) eje -en el primer cuadrante de un plano cartesiano.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/dZ2O3zwvuP0.

Ejemplo\(\PageIndex{2}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

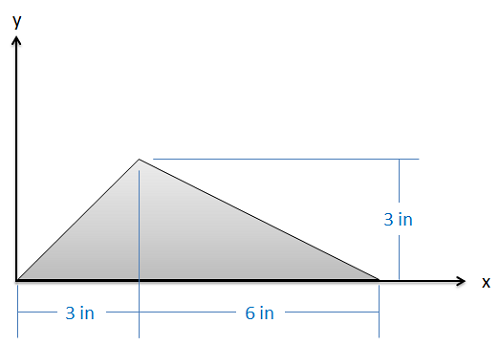
Un triángulo en el primer cuadrante de un plano de coordenadas cartesianas estándar. El lado más largo del triángulo, de 9 pulgadas de largo, comienza en el origen y se encuentra a lo largo del eje x. La intersección de los otros dos lados del triángulo se encuentra a 3 pulgadas a la derecha del origen y 3 pulgadas por encima del eje x. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un triángulo con su lado más largo acostado a lo largo del\(x\) eje -en el primer cuadrante de un plano cartesiano.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/hmGiCFwgIo8.

Ejemplo\(\PageIndex{3}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

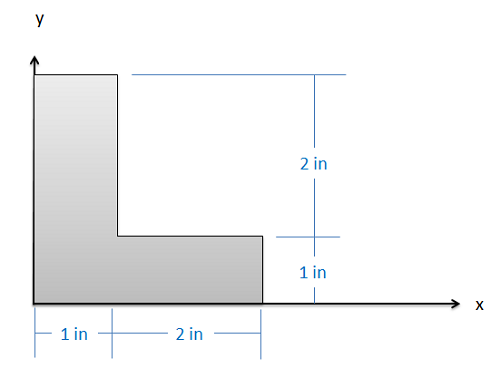
Una región en forma de L en el primer cuadrante de un plano de coordenadas cartesianas estándar. La forma consiste en un rectángulo de 3 pulgadas de largo y 1 pulgada de alto, que se extiende a lo largo del eje x con su esquina inferior izquierda en el origen, y un rectángulo de 1 pulgada de largo por 3 pulgadas de alto, que se extiende a lo largo del eje y con su esquina inferior izquierda en el origen. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una región en forma de L se encuentra a lo largo de\(y\) los ejes\(x\) - y -en el primer cuadrante de un plano cartesiano.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/4MHflda4FBw.