17.2: Sistemas sobredeterminados

Consideremos un sistema lineal sobredeterminado -como el que surge del ejemplo de regresión anterior- de la forma\[B z=g,\] o, más explícitamente,\[\left(\begin{array}{ll} B_{11} & B_{12} \\ B_{21} & B_{22} \\ B_{31} & B_{32} \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{l} g_{1} \\ g_{2} \\ g_{3} \end{array}\right) .\] Nuestro objetivo es encontrar\(z\) que haga verdadera la ecuación vectorial de tres componentes, es decir, encontrar la solución a la lineal sistema. En el Capítulo 16, consideramos el “problema hacia adelante” de la multiplicación matrizvector en la que, dado\(z\), calculamos\(g=B z\). También discutimos brevemente el problema “inverso” en el que dado\(g\) nos gustaría encontrar\(z\). Pero para\(m \neq n, B^{-1}\) no existe; como se discutió en el apartado anterior, puede\(z\) que no haya que satisfaga\(B z=g\). Así, tendremos que buscar una\(z\) que satisfaga la ecuación “de cerca” en el sentido que debemos especificar e interpretar. Este es el foco de esta sección. \({ }_{-}^{1}\)

\({ }^{1}\)Anote más adelante (en la Unidad V) veremos el caso ostensiblemente más sencillo en el que\(B\) es cuadrado y\(z\) existe una solución e incluso es única. Pero, por muchas razones, los sistemas sobredeterminados son un mejor lugar para comenzar.

Interpretación

Consideremos una interpretación de fila del sistema sobredeterminado. Satisfacer el sistema lineal requiere\[B_{i 1} z_{1}+B_{i 2} z_{2}=g_{i}, \quad i=1,2,3 .\] Tenga en cuenta que cada una de estas ecuaciones define una línea en\(\mathbb{R}^{2}\). Así, satisfacer las tres ecuaciones equivale a encontrar un punto que sea compartido por las tres líneas, lo que en general no es posible, como demostraremos en un ejemplo.

Ejemplo 17.2.1 Interpretación de filas del sistema sobredeterminado

Consideremos un sistema sobredeterminado\[\left(\begin{array}{cc} 1 & 2 \\ 2 & 1 \\ 2 & -3 \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 5 / 2 \\ 2 \\ -2 \end{array}\right)\] Usando la interpretación de filas del sistema lineal, vemos que hay tres ecuaciones lineales por satisfacer. El conjunto de puntos\(x=\left(x_{1}, x_{2}\right)\) que satisface la primera ecuación,\[1 \cdot x_{1}+2 \cdot x_{2}=\frac{5}{2},\] forman una línea\[L_{1}=\left\{\left(x_{1}, x_{2}\right): 1 \cdot x_{2}+2 \cdot x_{2}=5 / 2\right\}\] en el espacio bidimensional. De igual manera, los conjuntos de puntos que satisfacen la segunda y tercera ecuaciones forman líneas descritas por\[\begin{aligned} &L_{2}=\left\{\left(x_{1}, x_{2}\right): 2 \cdot x_{1}+1 \cdot x_{2}=2\right\} \\ &L_{3}=\left\{\left(x_{1}, x_{2}\right): 2 \cdot x_{1}-3 \cdot x_{2}=-2\right\} . \end{aligned}\] Estos conjuntos de puntos en\(L_{1}, L_{2}\), y\(L_{3}\), o las líneas, se muestran en la Figura 17.3 (a).

La solución al sistema lineal debe satisfacer cada una de las tres ecuaciones, es decir, pertenecer a las tres líneas. Esto significa que debe haber una intersección de las tres líneas y, si existe, la solución es la intersección. Este sistema lineal tiene la solución\[z=\left(\begin{array}{c} 1 / 2 \\ 1 \end{array}\right) .\] Sin embargo, tres líneas que se cruzan en\(\mathbb{R}^{2}\) es una ocurrencia rara; de hecho el lado derecho del sistema fue elegido cuidadosamente para que el sistema tenga una solución en este ejemplo. Si perturbaremos ya sea la matriz o el lado derecho del sistema, es probable que las tres líneas ya no se crucen.

Un sistema sobredeterminado más típico es el siguiente sistema,\[\left(\begin{array}{cc} 1 & 2 \\ 2 & 1 \\ 2 & -3 \end{array}\right)\left(\begin{array}{l} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 0 \\ 2 \\ -4 \end{array}\right)\] Nuevamente, interpretando la ecuación matricial como un sistema de tres ecuaciones lineales, podemos ilustrar el conjunto de puntos que satisfacen cada ecuación como una línea en\(\mathbb{R}^{2}\) como se muestra en la Figura 17.3 (b). No hay solución a este sistema sobredeterminado, porque no hay ningún punto\(\left(z_{1}, z_{2}\right)\) que pertenezca a las tres líneas, es decir, las tres líneas no se cruzan en un punto.

(a) sistema con una solución

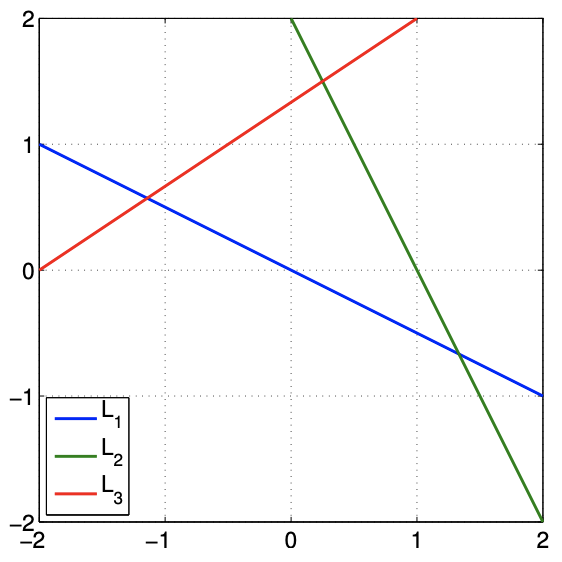
b) sistema sin solución

Figura 17.3: Ilustración de la interpretación de filas de los sistemas sobredeterminados. Cada línea es un conjunto de puntos que satisface\(B_{i} x=g_{i}, i=1,2,3\).

Interpretación de Columna

Consideremos ahora una interpretación de columna del sistema sobredeterminado. Satisfacer el sistema lineal requiere\[z_{1} \cdot\left(\begin{array}{l} B_{11} \\ B_{21} \\ B_{31} \end{array}\right)+z_{2} \cdot\left(\begin{array}{l} B_{12} \\ B_{22} \\ B_{32} \end{array}\right)=\left(\begin{array}{l} g_{1} \\ g_{2} \\ g_{3} \end{array}\right)\] En otras palabras, consideramos una combinación lineal de dos vectores en\(\mathbb{R}^{3}\) e intentamos coincidir con el lado derecho\(g \in \mathbb{R}^{3}\). Los vectores abarcan como máximo un plano en\(\mathbb{R}^{3}\), por lo que no hay peso\(\left(z_{1}, z_{2}\right)\) que haga que la ecuación se mantenga a menos que\(g\) el vector se encuentre en el plano. Para aclarar la idea, consideremos un ejemplo específico.

Ejemplo 17.2.2 Interpretación de columna del sistema sobredeterminado

\[\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{c} z_{1} \\ z_{2} \end{array}\right)=\left(\begin{array}{c} 1 \\ 3 / 2 \\ 2 \end{array}\right)\]La interpretación de la columna resulta en\[\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) z_{1}+\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right) z_{2}=\left(\begin{array}{c} 1 \\ 3 / 2 \\ 2 \end{array}\right)\] Al cambiar\(z_{1}\) y\(z_{2}\), podemos movernos en el plano\[\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right) z_{1}+\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right) z_{2}=\left(\begin{array}{c} z_{1} \\ z_{2} \\ 0 \end{array}\right)\]

Figura 17.4: Ilustración de la interpretación de columna del sistema sobredeterminado.

Claramente\(g_{3} \neq 0\), si, no es posible encontrar\(z_{1}\) y\(z_{2}\) que satisfagan la ecuación lineal,\(B z=g\). Es decir,\(g\) debe estar en el plano abarcado por las columnas de\(B\), que es el\(1-2\) plano en este caso.

La figura\(17.4\) ilustra la interpretación de columnas del sistema sobredeterminado. El vector\(g \in \mathbb{R}^{3}\) no se encuentra en el espacio abarcado por las columnas de\(B\), por lo tanto no hay solución al sistema. Sin embargo, si\(g_{3}\) es “pequeño”, entonces podemos encontrar un\(z^{*}\) tal que\(B z^{*}\) esté “cerca”\(g\), es decir, una buena aproximación a\(g\). Tal aproximación se muestra en la figura, y en la siguiente sección se analiza cómo encontrar tal aproximación.