26.5: Sistemas Tridiagonales

Si bien el costo de la eliminación gaussiana escala como\(n^{3}\) para un sistema\(n \times n\) lineal general, hay casos en los que el escalado es mucho más débil y por lo tanto el costo computacional para un problema grande es relativamente bajo. Un sistema tridiagonal es uno de esos ejemplos. Un sistema tridigonal se caracteriza por tener entradas distintas de cero solo a lo largo de la diagonal principal y la diagonal superior e inferior inmediata, i.e.

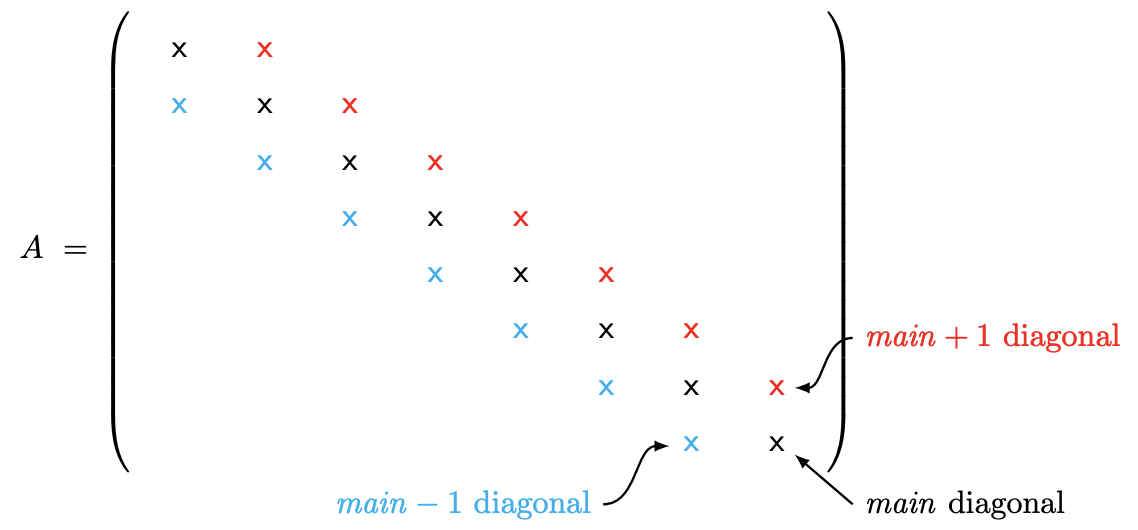
La diagonal superior inmediata se llama súper diagonal y la diagonal inferior inmediata se llama subdiagonal. Se logra una reducción significativa en el costo computacional aprovechando la escasez de la matriz tridiagonal. Es decir, omitimos la adición y multiplicación de un gran número de ceros presentes en la matriz.

Apliquemos la eliminación gaussiana a la matriz\(n \times n\) tridiagonal. En el primer paso, calculamos el factor de escalado (un FLOP), escalamos la segunda entrada del coeficiente de la primera fila por el factor de escala (un FLOP) y lo agregamos al segundo coeficiente de la segunda fila (un FLOP). (Tenga en cuenta que no necesitamos escalar y sumar el primer coeficiente de la primera ecuación al de la segunda ecuación porque sabemos que desaparecerá por construcción.) No tenemos que sumar la primera ecuación a ninguna otra ecuación porque el primer coeficiente de todas las demás ecuaciones es cero. Además, tenga en cuenta que la adición de la primera fila (escalada) a la segunda fila no introduce ninguna nueva entrada distinta de cero en la segunda fila. Así, la matriz actualizada tiene ceros por encima de la superdiagonal y conserva la estructura tridiagonal de la matriz original (con la\((2,1)\) entrada eliminada, por supuesto); en particular, el\((n-1) \times(n-1)\) subbloque actualizado vuelve a ser tridiagonal. También modificamos el lado derecho multiplicando la primera entrada por el factor de escala (un FLOP) y agregándola a la segunda entrada (un FLOP). Combinado con los tres FLOP requeridos para la manipulación de la matriz, el costo total para el primer paso es de cinco FLOP.

De igual manera, en el segundo paso, utilizamos la segunda ecuación para eliminar el coeficiente principal distinto de cero de la tercera ecuación. Debido a que la estructura del problema es idéntica a la primera, esto también requiere cinco FLOP. La matriz actualizada conserva la estructura tridiagonal en esta etapa de eliminación y, en particular, el\((n-2) \times(n-2)\) subbloque actualizado es tridiagonal. Repitiendo la operación para\(n\) escalones, el costo total para producir un sistema triangular superior (y el lado derecho modificado asociado) es\(5 n\) FLOP. Tenga en cuenta que el costo de eliminación gaussiana para un sistema tridiagonal escala linealmente con el tamaño del problema\(n\): una mejora dramática en comparación con\(\mathcal{O}\left(n^{3}\right)\) las operaciones requeridas para un caso general.

En este punto, hemos producido un sistema triangular superior de la forma

Se dice que el sistema es bidiagonal -o más precisamente bidiagonal superior- ya que las entradas distintas de cero aparecen solo en la diagonal principal y la súper diagonal. (También se dice que una matriz que tiene entradas distintas de cero solo en la principal y subdiagonal es bidiagonal; en este caso, sería bidiagonal inferior).

En la etapa de sustitución posterior, podemos aprovechar nuevamente la escasez -en particular la estructura bidiagonal- de nuestro sistema triangular superior. Como antes, la evaluación de\(u_{n}\) requiere una división simple (un FLOP). La evaluación de\(u_{n-1}\) requiere una resta a escala\(u_{n}\) del lado derecho (dos FLOP) y una división (un FLOP) para tres FLOP totales. La estructura es la misma para las\(n-2\) incógnitas restantes; la evaluación de cada entrada toma tres FLOP. Por lo tanto, el costo total de la sustitución posterior para una matriz bidiagonal es\(3 n\) FLOP. Combinado con el costo de la eliminación gaussiana para la matriz tridiagonal, el costo general para resolver un sistema tridiagonal es\(8 n\) FLOP. Así, el recuento de operaciones de todo el procedimiento de solución lineal (eliminación gaussiana y sustitución posterior) escala linealmente con el tamaño del problema para matrices tridiagonales.

Hemos logrado una reducción significativa en el costo computacional para un sistema tridiagonal en comparación con un caso general aprovechando la estructura de sparsity. En particular, el costo computacional se ha reducido de\(2 n^{3} / 3\) a\(8 n\). Por ejemplo, si queremos resolver para el desplazamiento de equilibrio de un sistema de\(n=1000\) masa de resorte (que produce un sistema tridiagonal), hemos reducido el número de operaciones de un orden de mil millones a mil. De hecho, con el algoritmo de matriz tridiagonal que aprovecha el patrón de dispersidad, podemos resolver fácilmente un sistema de masa de resorte con millones de incógnitas en una máquina de escritorio; este ciertamente no sería el caso si se emplea el algoritmo general de eliminación gaussiana, lo que requeriría \(\mathcal{O}\left(10^{18}\right)\)operaciones.

Si bien muchos problemas en ingeniería requieren la solución de un sistema lineal con millones (o incluso miles de millones) de incógnitas, estos sistemas suelen ser escasos. (Si bien estos sistemas rara vez son tridiagonales, la mayoría de las entradas de estas matrices son cero, sin embargo). En el siguiente capítulo, consideramos la solución a sistemas lineales dispersos más generales; tal como observamos en este caso tridiagonal, la clave para reducir el costo computacional de las matrices dispersas grandes -y por lo tanto hacer que el cálculo sea manejable- es estudiar el patrón distinto de cero de la matriz dispersa y diseñar un algoritmo que no ejecuta operaciones innecesarias.