27.3: Eliminación gaussiana y sustitución de espalda

Eliminación Gaussiana

Ahora consideramos el recuento de operaciones asociado con la resolución de un sistema lineal escaso\(A u=f\) utilizando la eliminación gaussiana y la sustitución posterior introducida en el capítulo anterior. Recordemos que la eliminación gaussiana es un proceso de convertir un sistema lineal en un sistema triangular superior, es decir,\[\operatorname{STEP} 1: A u=f \rightarrow \underset{\substack{(n \times n) \\ \text { upper } \\ \text { triangular }}}{U} \quad u=\hat{f}\] Para una matriz\(n \times n\) densa, la eliminación gaussiana requiere aproximadamente\(\frac{2}{3} n^{3} \mathrm{FLOPs}^{\mathrm{S}}\).

Sistemas de bandas densamente poblados

Ahora, consideremos una matriz de\(n \times n\) bandas con ancho de banda\(m_{\mathrm{b}}\). Para analizar el peor de los casos, asumimos que todas las entradas dentro de la banda son distintas de cero. En el primer paso de la eliminación gaussiana, identificamos la primera fila como la “fila de pivote” y eliminamos la primera entrada (columna 1) de las primeras\(m_{\mathrm{b}}\) filas agregando fila pivotante apropiadamente escalada; la columna 1 de filas ya\(m_{\mathrm{b}}+2, \ldots, n\) es cero. La eliminación de la columna 1 de una fila dada requiere la adición de\(m_{\mathrm{b}}+1\) entradas escaladas de la fila de pivote, lo que requiere\(2\left(m_{\mathrm{b}}+1\right)\) operaciones. Aplicando la operación a\(m_{\mathrm{b}}\) filas, el recuento de operaciones para el primer paso es aproximadamente\(2\left(m_{\mathrm{b}}+1\right)^{2}\). Tenga en cuenta que debido a que las entradas distintas de cero de la fila de pivote se limitan a\(m_{\mathrm{b}}+1\) las primeras entradas, la adición de la fila pivotante escalada a las primeras\(m_{\mathrm{b}}+1\) filas no aumenta el ancho de banda del sistema (ya que estas filas ya tienen entradas distintas de cero en estas columnas). En particular, el patrón de dispersidad de la parte superior de\(A\) está inalterado en el proceso.

El segundo paso de eliminación gaussiana puede interpretarse como aplicar el primer paso de eliminación gaussiana a la\((n-1) \times(n-1)\) submatriz, que en sí misma es una matriz de bandas con un ancho de banda\(m_{\mathrm{b}}\) (ya que el primer paso no altera el ancho de banda de la matriz). Así, la segunda etapa de eliminación también requiere aproximadamente\(2\left(m_{\mathrm{b}}+1\right)^{2}\) FLOs. Repitiendo la operación para todos los\(n\) pivotes de la matriz, el recuento total de operaciones para la eliminación gaussiana es aproximadamente\(2 n\left(m_{\mathrm{b}}+1\right)^{2} \sim \mathcal{O}(n)\). La matriz triangular superior final\(U\) toma la siguiente forma:

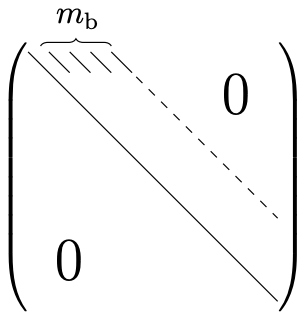
La matriz triangular superior tiene aproximadamente entradas distintas de\(n\left(m_{\mathrm{b}}+1\right) \sim \mathcal{O}(n)\) cero. Tanto el conteo de operaciones como el número de distintos de cero en la matriz triangular superior final son\(\mathcal{O}(n)\), en comparación con\(\mathcal{O}\left(n^{3}\right)\) operaciones y\(\mathcal{O}\left(n^{2}\right)\) entradas para un sistema denso. (Asumimos aquí\(m_{\mathrm{b}}\) es fijo independiente de\(n\).)

En particular, como se discutió en el capítulo anterior, la eliminación gaussiana de una matriz tridiagonal produce una matriz bidiagonal superior\[U=\left(\_{\text {main, main }+1 \text { diagonals }}^{0}\right.\] en aproximadamente\(5 n\) operaciones (incluyendo la formación del lado derecho modificado\(\hat{f}\)). De igual manera, la eliminación gaussiana de un sistema pentadiagonal da como resultado una matriz triangular superior de la forma\[U=(\underbrace{0}_{\text {main, main }+1,+2 \text { diagonals }}\] y requiere aproximadamente\(14 n\) operaciones.

Sistemas “Outrigger”: Rellenos

Ahora consideremos la aplicación de la eliminación gaussiana a un sistema de “soporte”. Primero, debido a que un sistema\(n \times n\) “estabilizante” con ancho de banda\(m_{\mathrm{b}}\) es un caso especial de un sistema “densamente poblado por bandas” con un ancho de banda\(m_{\mathrm{b}}\) considerado anteriormente, sabemos que el recuento de operaciones para la eliminación gaussiana es como máximo\(n\left(m_{\mathrm{b}}+1\right)^{2}\) y el número de distinto de cero en la matriz triangular superior es como máximo\(n\left(m_{\mathrm{b}}+1\right)\). Además, debido a un gran número de entradas cero entre las bandas externas de la matriz, esperamos que el recuento de operaciones y el número de no cero sean menores que los del caso “densamente poblado por bandas”. Desafortunadamente, la inspección del procedimiento de eliminación gaussiana revela que esta reducción en el costo y almacenamiento no se logra en general.

La incapacidad para reducir el recuento de operaciones se debe a la introducción de “rellenos”: las entradas de la matriz dispersa que originalmente son cero pero que se convierten en distintas de cero en el proceso de eliminación gaussiana. La introducción de los rellenos se describe mejor gráficamente. La figura\(\underline{27.3}\) muestra una secuencia de matrices generadas a través de la eliminación gaussiana de\(25 \times 25\) un sistema de soporte. En las figuras posteriores, coloreamos entradas de código de parcialmente procesadas\(U\): el área sombreada representa filas o columnas de pivotes ya procesadas; el área no sombreada representa las filas y columnas de pivotes aún no procesadas; el azul representa nonceros iniciales en\(A\) que permanecen sin ceros en\(U\) a-ser; y los rojos son ceros iniciales de los\(A\) cuales se convierten en distintos de cero en\(U\) a-ser, es decir, rellenos.

Como muestra la Figura 27.3 (a), el ancho de banda de la matriz original es\(m_{\mathrm{b}}=5\). (Los valores de las entradas están ocultos en la figura ya que no son importantes en esta discusión de rellenos). En el primer paso de eliminación, primero eliminamos la columna 1 de la fila 2 agregando una fila 1 apropiadamente escalada a la fila. Si bien logramos eliminar la columna 1 de la fila 2, tenga en cuenta que introducimos un elemento distinto de cero en la columna 6 de la fila 2 ya que la columna 6 de la fila 1 “cae” a la fila 2 en el proceso de eliminación. Este elemento distinto de cero se llama “relleno”. De igual manera, al eliminar la columna 1 de la fila 6, introducimos un “relleno” en la columna 2 ya que la columna 2 de la fila 1 “cae” a la fila 6 en el proceso de eliminación. Así, hemos introducido dos rellenos en esta primera etapa de eliminación como se muestra en la Figura 27.3 (b): uno en la parte superior y otro en la parte inferior.

Ahora, considere el segundo paso de eliminación a partir de la Figura 27.3 (b). Primero eliminamos la columna 2 de la fila 3 agregando la fila 2 a la fila 3 apropiadamente escalada. Esta vez, introducimos el relleno no sólo de la columna 7 de la fila 2 “cayendo” a la fila 3, sino también de la columna 6 de la fila 2 “cayendo” a la fila 3. Tenga en cuenta que este último es de hecho un relleno introducido en el primer paso. En general, una vez que se introduce un relleno en la parte superior, el relleno se propaga de un paso a otro, introduciendo más rellenos a medida que “cae”. A continuación, necesitamos eliminar la columna 2 de la fila 6; esta entrada era cero en la matriz original pero se rellenó en el primer paso de eliminación. Así, el relleno introducido en la parte inferior aumenta el número de filas cuya entrada principal debe ser eliminada en el proceso de triangulación superior. La matriz después del segundo paso se muestra en la Figura 27.3 (c). Tenga en cuenta que el número de rellenos continúan aumentando, y comenzamos a perder las entradas cero entre las bandas externas del sistema de soporte.

Como se muestra en la Figura\(\underline{27.3(\mathrm{e})}\), al inicio del quinto paso de eliminación, el “soporte”

a) sistema original\(A\)

b) inicio del paso\(2, \tilde{U}(k=1)\)

c) inicio del paso\(3, \tilde{U}(k=2)\)

(d) inicio del paso\(4, \tilde{U}(k=3)\)

e) inicio del paso\(5, \tilde{U}(k=4)\)

(f) inicio del paso\(15, \tilde{U}(k=14)\)

Figura 27.3: Ilustración de la eliminación gaussiana aplicada a un sistema de\(25 \times 25\) “soporte”. Las entradas azules son las entradas presentes en el sistema original, y las entradas rojas son “rellenadas” introducidas en el proceso de factorización. El pivote para cada paso está marcado por un cuadrado rojo.

ha perdido en gran medida su estructura dispersa en el\(\left(m_{\mathrm{b}}+1\right) \times\left(m_{\mathrm{b}}+1\right)\) subbloque principal de la submatriz de trabajo. Así, para las\(n-m_{\mathrm{b}}\) etapas posteriores de eliminación gaussiana, cada paso toma\(2 m_{\mathrm{b}}^{2}\) FLOP, que es aproximadamente el mismo número de operaciones que el caso de bandas densamente poblado. Así, el número total de operaciones requeridas para la eliminación gaussiana de un sistema de soporte es aproximadamente\(2 n\left(m_{\mathrm{b}}+1\right)^{2}\), el mismo que el caso de bandas densamente pobladas. La matriz final toma la forma:

Tenga en cuenta que el número de entradas distintas de cero es aproximadamente\(n\left(m_{\mathrm{b}}+1\right)\), que es mucho mayor que el número de entradas distintas de cero en el sistema “estabilizante” original.

El sistema “estabilizante”, como el considerado anteriormente, surge naturalmente cuando una ecuación diferencial parcial (PDE) se discretiza en dos o mayores dimensiones usando una diferencia finita o formulación de elementos finitos. Un ejemplo de tal PDE es la ecuación de calor, que describe, por ejemplo, la temperatura de equilibrio de un sistema térmico mostrado en la Figura\(27.4\). Con un orden natural de los grados de libertad del sistema discretizado, el ancho de banda\(m_{\mathrm{b}}\) es igual al número de puntos de cuadrícula en una dirección de coordenadas, y el número de grados de libertad del sistema lineal es\(n=m_{\mathrm{b}}^{2}\) (es decir, producto del número de puntos de cuadrícula en dos direcciones de coordenadas). En otras palabras, el ancho de banda es la raíz cuadrada del tamaño de la matriz, es decir\(m_{\mathrm{b}}=n^{1 / 2}\). Debido a la estructura de soporte del sistema resultante, factorizar el sistema requiere aproximadamente\(n\left(m_{\mathrm{b}}+1\right)^{2} \approx n^{2}\) FLOP. Esto contrasta con el caso unidimensional, que produce un sistema tridiagonal, que puede resolverse en\(\mathcal{O}(n)\) operaciones. De hecho, en tres dimensiones, el ancho de banda es igual al producto del número de puntos de cuadrícula en dos direcciones de coordenadas, i.e\(m_{\mathrm{b}}=\left(n^{1 / 3}\right)^{2}=n^{2 / 3}\). El número de operaciones requeridas para la factorización es\(n\left(m_{\mathrm{b}}+1\right)^{2} \approx n^{7 / 3}\). Así, el costo de resolver una PDE es significativamente mayor en tres dimensiones que en una dimensión aunque ambos sistemas discretizados tuvieran el mismo número de incógnitas. \({ }_{-}\)

Sustitución de espalda

Habiendo analizado el recuento de operaciones para la eliminación gaussiana, inspeccionemos el recuento de operaciones para la sustitución posterior. En primer lugar, recordemos que la sustitución por retroceso es un proceso de encontrar la solución de un sistema triangular superior,\[\text { STEP 2: } U u=\hat{f} \rightarrow u .\] es decir, recordar que el recuento de operaciones para la sustitución posterior es igual al doble del número de entradas distintas de cero en\(U\). Debido a que la matriz\(U\) está inalterada, podemos simplemente contar el número de

\({ }^{1}\)No incógnitas por dimensión, sino el número total de incógnitas.

Figura 27.4: Ecuación de calor en dos dimensiones. La discretización de la ecuación por el método de diferencia finita (FD) o elemento finito (FE) produce un sistema de “soporte”.

entradas distintas de cero en las\(U\) que obtenemos después de la eliminación gaussiana; no hay nada equivalente a “fill-in” - modificaciones a la matriz que incrementa el número de entradas en la matriz y de ahí el conteo de operaciones - en sustitución posterior.

Sistemas de bandas densamente poblados

Para un sistema de bandas densamente poblado con ancho de banda\(m_{\mathrm{b}}\), el número de incógnitas en la matriz factorizada\(U\) es aproximadamente igual a\(n\left(m_{\mathrm{b}}+1\right)\). Por lo tanto, la sustitución posterior requiere aproximadamente\(2 n\left(m_{\mathrm{b}}+1\right)\) FLOs. En particular, la sustitución posterior por un sistema tridiagonal (que produce una bidiagonal superior\(U\)) requiere aproximadamente\(3 n\) FLOP. Un sistema pentadiagonal requiere aproximadamente\(5 n\) FLOP.

“Soporte”

Como se discutió anteriormente,\(n \times n\) una matriz estabilizadora de ancho de banda\(m_{\mathrm{b}}\) produce una matriz triangular superior\(U\) cuyas entradas entre la diagonal principal y la banda externa son distintas de cero debido a los rellenos. Así, el número de nonceros in\(U\) es aproximadamente\(n\left(m_{\mathrm{b}}+1\right)\), y el recuento de operaciones para la sustitución posterior es aproximadamente\(2 n\left(m_{\mathrm{b}}+1\right)\). (Obsérvese en particular que aunque un sistema de soporte solo tenga cinco bandas (como en la que se muestra en la Figura\(27.3\)), el número de operaciones para la sustitución posterior es\(2 n\left(m_{\mathrm{b}}+1\right)\) y no\(5 n\). \()\)