2.1: Tensor de estrés

Comenzamos con la presentación de conceptos simples en una y dos dimensiones antes de introducir un concepto general del tensor de tensión. Considerar una barra prismática de sección transversal cuadrada sometida a una fuerza de tracción\(F\),

Figura\(\PageIndex{1}\): Una barra larga con tres cortes diferentes en\(\theta, \theta = 0\) y\(\pi/2 − \theta\).

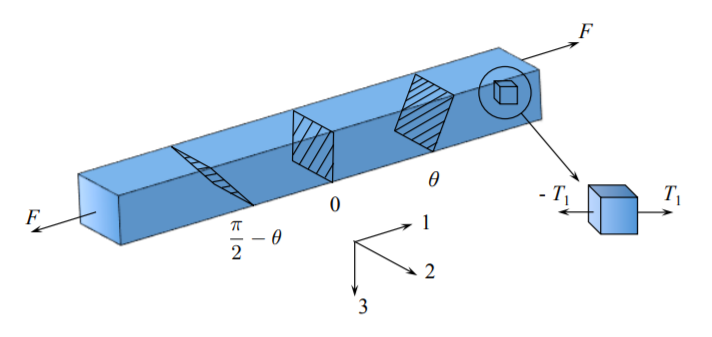
La fuerza por unidad de área se llama tracción superficial\(T\):

\[T = \sigma = \frac{\text{force}}{\text{area}} = \frac{F}{A_o} \left[ \frac{\mathrm{N}}{\mathrm{mm}^2} \right] \label{2.1.1}\]

En el caso uniaxial, la fracción superficial es el único componente del tensor de tensión en el sistema de coordenadas global, comúnmente conocido como\(\sigma\).

¿Cómo se puede aplicar una fuerza a la sección final de una barra? Esto se puede hacer de varias maneras diferentes (ver Figura (\(\PageIndex{2}\))). Una conexión de pasador se puede pegar (o soldar) a la sección final, o se puede perforar un orificio a través de la barra para unir un pasador.

Figura\(\PageIndex{2}\): Cómo aplicar tensión al extremo de una barra.

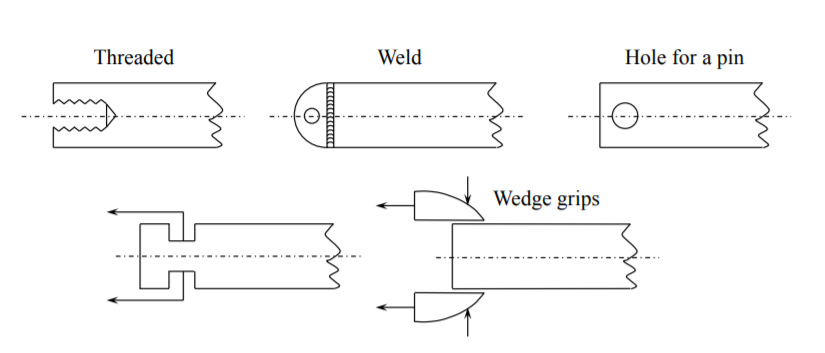
O se puede mecanizar una rosca interna o externa. Finalmente, la fuerza axial podría ser aplicada a través de agarres friccionales o mecánicos. Excepto el conector soldado o pegado, se crea un estado complejo de tensión cerca de los extremos de la barra donde el estado de tensión es multiaxial. Dichos estados de tensión se limitan a un segmento relativamente corto de la barra comparable con la altura o diámetro de la barra. A lo largo de esta sección se produce una transición gradual del estado multiaxial de tensión al estado uniaxial, para lo cual se mantiene la Ecuación\ ref {2.1.1}.

Nota

El ejemplo anterior sirve como aplicación práctica del principio de Saint-Venant (1856). Este principio que lleva el nombre del teórico francés de la elasticidad, Jean Claude Barre' de Saint-Venant puede afirmarse como: “la diferencia entre los efectos de dos cargas diferentes pero estáticamente equivalentes se vuelve muy pequeña a distancias suficientemente grandes de la carga”.

¿Piensa cuáles son las “dos” cargas equivalentes que se aplican a los extremos de las barras? Por lo general pensamos en una sección transversal que se corta perpendicular al eje de la barra. Consideremos ahora dos cortes en los ángulos\(\theta\) y\(\left(\frac{\pi}{2} - \theta \right)\) a la dirección normal. Los planos están definidos por el vector normal unitario\(\boldsymbol{n}\).

Figura\(\PageIndex{3}\): Fuerzas normales y tangenciales que actúan sobre la sección inclinada de la barra.

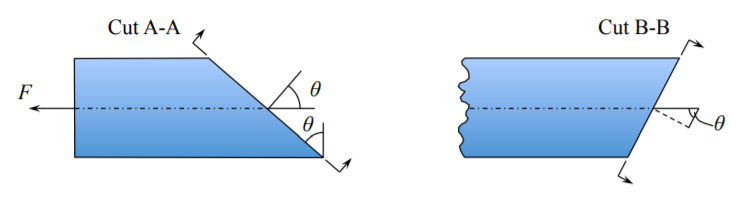
Del diagrama de cuerpo libre, los componentes de las fuerzas normales y tangenciales:

\[F_{\mathrm{N}} = F \cos \theta \label{3.1.2}\]

\[F_{\mathrm{n}} = F \cos (\frac{\pi}{2} - \theta)\]

\[F_{\mathrm{T}} = F \sin \theta\]

\[F_{\mathrm{t}} = F \sin (\frac{\pi}{2} - \theta) \label{3.1.5}\]

La sección transversal inclinada\(A\) es mayor y está relacionada con la sección transversal de referencia por

\[A_o = A_{\mathrm{A}} \cos \theta, \; A_o = A{\mathrm{B}} \cos (\frac{\pi}{2} - \theta)\]

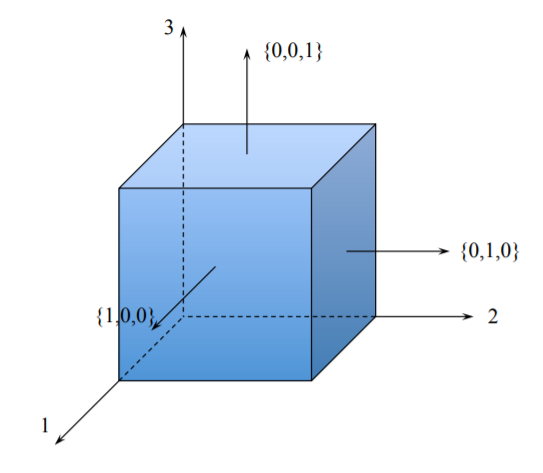
Consideremos ahora un elemento cúbico de volumen unitario ubicado en las intersecciones de los cortes A-A y B-B, Figura (\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): El elemento volumétrico con tracción superficial que actúa sobre dos facetas adyacentes.

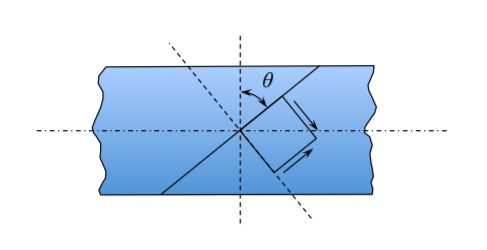
La tracción superficial (fuerza por unidad de área) en las dos facetas perpendiculares son

\[\text{Facet parallel to A-A:} \quad T_{\mathrm{n}} = T \cos^2 \theta\]

\[T_{\mathrm{t}} = T \sin \theta \cos \theta \label{3.1.8}\]

\[\text{Facet parallel to B-B:} \quad T_{\mathrm{n}} = T \cos^2 (\frac{\pi}{2} - \theta)\]

\[T_{\mathrm{t}} = T \sin (\frac{\pi}{2} - \theta) \cos (\frac{\pi}{2} - \theta)\]

Se puede observar que los componentes tangenciales del vector de tracción superficial en cortes A-A y B-B son idénticos. Las gráficas normalizadas de las cantidades anteriores versus el ángulo de orientación de la sección transversal se muestran en la Figura (\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Valores relativos de componentes normales y cortantes de la tracción superficial en función de la orientación del corte.

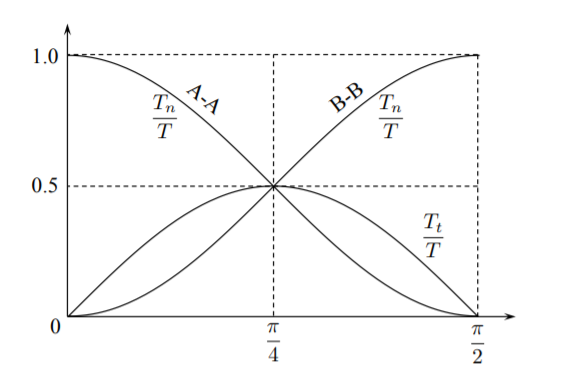
Se puede observar que el componente tangencial alcanza el máximo en\(45^{\circ}\). Esto significa que si el material falla debido a la carga de cizallamiento, la superficie de fractura siempre estará orientada a\(45^{\circ}\). El ejemplo anterior nos enseña que existen infinitas combinaciones de componentes normales y tangenciales de tracciones superficiales que están en equilibrio con la carga aplicada. Para cada orientación de la sección transversal hay un par diferente de\(\{T_{\mathrm{n}}, T_{\mathrm{t}}\}\). La orientación del elemento de superficie está definida de manera única por el vector normal unitario\(\boldsymbol{n}\{n_1, n_2, n_3\}\). Al mismo tiempo lo son los componentes del vector de tracción superficial que actúa sobre el mismo elemento\(\boldsymbol{T}\{T_1, T_2, T_3\}\).

Los componentes del vector de tracción superficial que actúa sobre este elemento superficial son\(\boldsymbol{T}\{T_1, T_2, T_3\}\). Por ejemplo, la orientación de las facetas del cubo de material unitario se muestra en la Figura (\(\PageIndex{6}\)).

Figura\(\PageIndex{6}\): Componentes del vector normal unitario en facetas de un cubo unitario.

La relación entre los vectores de tracciones superficiales, el vector normal unitario que define el elemento superficial y el tensor de tensión están dadas por la famosa fórmula de Cauchy

\[T_i = T_{ij}n_j\]

o en la notación ampliada,

\[T_1 = \sigma_{1j}n_j = \sigma_{11}n_1 + \sigma_{12}n_2 + \sigma_{13}n_3\]

\[T_2 = \sigma_{2j}n_j = \sigma_{21}n_1 + \sigma_{22}n_2 + \sigma_{23}n_3 \label{3.1.13}\]

\[T_3 = \sigma_{3j}n_j = \sigma_{31}n_1 + \sigma_{32}n_2 + \sigma_{33}n_3\]

En gran medida la relación Cauchy es análoga a la relación deformación-desplazamiento puesta en forma de Ecuaciones\ ref {3.1.2} -\ ref {3.1.5}.

\[du_i = F_{ij}dx_j\]

El gradiente de desplazamiento\(F_{ij}\) transforma el incremento del elemento length\(dx_j\) en el incremento de desplazamiento\(du_i\). De la misma manera el tensor de tensión transforma la orientación del elemento superficial\(\boldsymbol{n}\) en la tracción superficial que actúa sobre este elemento.

Para obtener una interpretación física del concepto del tensor de tensión, veamos cómo funciona la fórmula de Cauchy en el caso de problemas unidimensionales y bidimensionales de la barra cargada axialmente. Considera primero el corte normal de la barra con el eje longitudinal como 1 eje. Los componentes de las tracciones superficiales se dan en la Figura (\(\PageIndex{7}\)). Los componentes correspondientes del vector normal unitario se definieron en la Figura (\(\PageIndex{6}\)), donde\(T = \frac{F}{A_o}\).

Figura\(\PageIndex{7}\): El elemento de volumen unitario alineado con el eje de la barra.

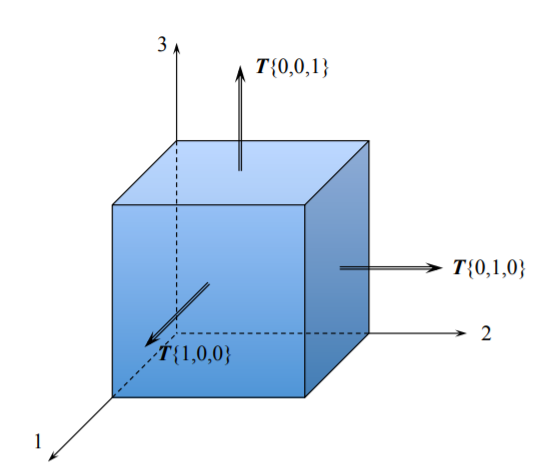
Sustituyendo los valores de los componentes de los dos vectores en Ecuación\ ref {3.1.13} se obtienen las siguientes expresiones:

\ [\ begin {array} {c|c|c}
\ nombreoperador {Faceta} (1,0,0) &\ nombreoperador {Faceta} (0,1,0) &\ nombre_operador {Faceta} (0,0,1)\\
T_1 =\ sigma_ {11} & 0 =\ sigma_ {12} & 0=\ sigma_ {13}\\
0 =\ sigma_ {21} & 0 =\ sigma_ {22} & 0=\ sigma_ {23}\\
0=\ sigma_ {31 } & 0=\ sigma_ {32} & 0=\ sigma_ {33}
\ final {matriz}\]

Por lo tanto, los componentes de la\(3 \times 3\) matriz de tensión en el sistema de coordenadas global son

\ [\ boldsymbol {\ sigma} =\ begin {vmatrix}
T & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 & 0
\ end {vmatrix}\ label {3.1.17}\]

Este es el estado uniaxial de estrés. El ejemplo bidimensional del corte inclinado es mucho más interesante. Esta vez se utilizará un sistema de coordenadas locales, girado con respecto a los 3 ejes. En este sistema los componentes\(\boldsymbol{n}\) son los mismos que en el sistema global. Los componentes del vector de tracción superficial en tres facetas, calculados en la Ecuación\ ref {3.1.8} se definen en la Figura (\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\): Componentes de las tracciones superficiales en el elemento de volumen girado.

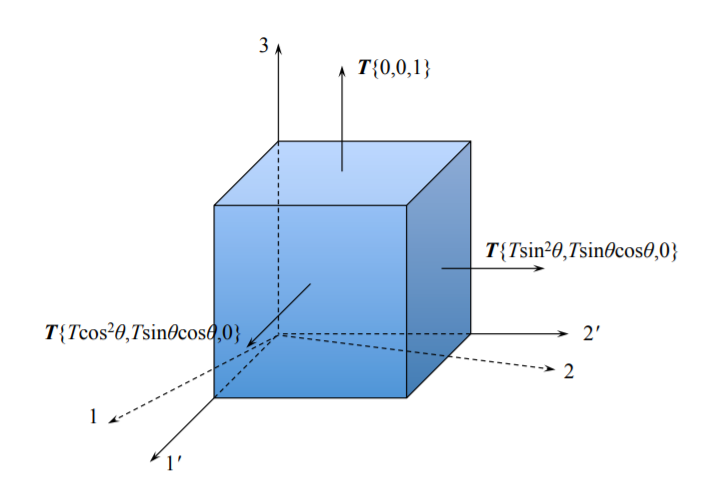
Sustituyendo los valores anteriores en la fórmula de Cauchy obtenemos

\ [\ begin {array} {c|c|c}
\ nombreoperador {Faceta} (1,0,0) &\ nombreoperador {Faceta} (0,1,0) &\ nombreoperador {Faceta} (0,0,1)\\
T\ cos ^ {2}\ theta=\ sigma_ {11} & T\ sin\ theta\ cos\ theta=\ sigma_ {12} & 0=\ sigma_ {13}\\
T\ sin\ theta\ cos\ theta=\ sigma_ {21} & T\ sin ^ {2}\ theta=\ sigma_ {22} & 0=\ sigma_ {23}\\
0=\ sigma_ {31} & 0=\ sigma_ {32} & 0=\ sigma_ {33}
\ end {array}\]

Los componentes de tensión plana del tensor de tensión son

\ [\ negrita {\ sigma} =\ comenzar {vmatrix}
T\ cos^ {\ theta} & T\ sin\ theta\ cos\ theta & 0\\ T\ sin\ theta\ cos\ theta & T\ sin^ {2}\ theta & 0\ 0 & 0 & 0
\ end {vmatrix}\ etiqueta {3.1.19}\]

Es interesante que las matrices Ecuación\ ref {3.1.17} y Ecuación\ ref {3.1.19} representan el mismo estado de tensión visto en dos sistemas de coordenadas girados uno con respecto al otro. La transformación del tensor de tensión de un sistema de coordenadas a otro es la asignatura Recitación 1 donde la relación entre la Ecuación\ ref {3.1.17} y la Ecuación\ ref {3.1.19} se derivará de una manera diferente.

Simetría del tensor de tensión

También hay que señalar de la Ecuación\ ref {3.1.19} que el tensor de tensión es simétrico significando que\(\sigma_{12} = \sigma_{21}\). La simetría del tensor de tensión proviene de la ecuación de equilibrio de momento de son elementos de volumen infinitesimal. En general

\[\sigma_{ij} = \sigma_{ji}\]

La simetría del tensor de tensión reduce los nueve componentes de la\(3 \times 3\) métrica a solo seis componentes independientes. A continuación se explica el significado de los dos subíndices del tensor de tensión

\[\sigma_{??}\nonumber\]

El primer subíndice define el plano sobre el que están actuando las tracciones superficiales. Por ejemplo, “1” denota el elemento de superficie perpendicular al eje\(x_1\). El segundo subíndice indica la dirección de un componente particular de las tracciones superficiales. Esta convención se explica en la Figura (\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): Componentes del tensor de tensión en tres facetas del elemento de superficie infinitesimal.

Convención de Firmar

La fórmula de Cauchy también se puede utilizar consistentemente para determinar el signo de los componentes del tensor de tensión. El punto es que el signo de los componentes de los vectores se conoce a partir del sistema de coordenadas elegido. Para ilustración, orientemos el elemento de volumen a lo largo del\(x_1\) eje. Con dirección positiva a la derecha.

Figura\(\PageIndex{10}\): Explicación de la convención de signos del tensor de estrés.

De la fórmula de Cauchy

\[T_1 = \sigma_{11}n_1 \label{3.1.21}\]

En la faceta derecha tanto la tracción superficial como el vector normal unitario son positivos y así debe ser el componente normal del tensor de tensión\(\sigma_{11}\). En la faceta izquierda\(T_1\) tanto como al\(x_1\) eje. Para que la Ecuación\ ref {3.1.21} mantenga el componente\(\sigma_{11}\) debe ser positivo, aunque su visualización apunte en la dirección negativa. en el ejemplo anterior el estado de tensión es uniforme a lo largo del\(x_1\) eje. Este es el caso de una barra bajo tensión. En general existe un gradiente de los componentes del tensor de tensión de manera que las tensiones en ambos lados del elemento infinitesimal difieren en una pequeña cantidad de\(d\sigma_{11}\). La convención de signos está abriendo el camino para derivar las ecuaciones de equilibrio para el continuo 3-D. Este tema es el tema de la siguiente sección.

Equilibrio

La ecuación de equilibrio para un elemento de volumen infinitesimal se deriva primero usando dos métodos. Haciendo referencia a la Figura (\(\PageIndex{9}\)), se indican en la Figura (\(\PageIndex{11}\)) solo aquellos componentes del tensor de tensión que se dirigen a lo largo\(x_2\) del eje. Estos son\(\sigma_{12}\),\(\sigma_{22}\) y\(\sigma_{32}\).

Figura\(\PageIndex{11}\): Todos los componentes del tensor de tensión que contribuyen al equilibrio de fuerzas en\(x_2\) dirección deben estar en equilibrio.

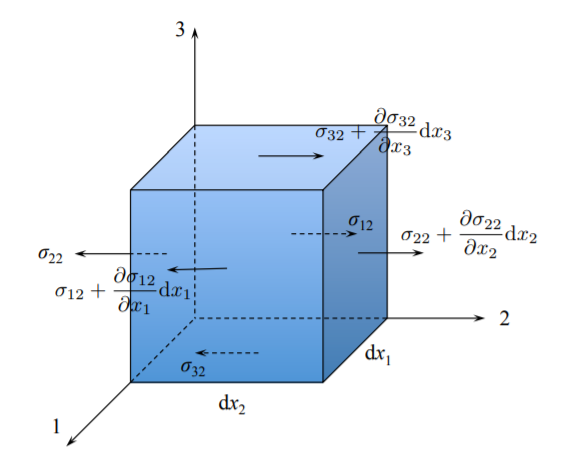
Según la ley de Newton, la suma de todas las fuerzas (tensión por el área superficial) que actúan a lo largo\(x_2\) debe ser cero

\[\left( \sigma_{22} + \frac{\partial \sigma_{22}}{\partial x_2} dx_2 \right) dx_1 dx_3 - \sigma_2 dx_1 dx_3 + \left( \sigma_{12} + \frac{\partial \sigma_{12}}{\partial x_1}dx_1\right) dx_2 dx_3 - \sigma_{12} dx_2 dx_3 + \left( \sigma_{32} + \frac{\partial \sigma_{32}}{\partial x_3}dx_3\right) dx_1 dx_2 - \sigma_{32} dx_1 dx_2 + B_2 dx_1 dx_2 dx_3 = 0\]

Por generalidad, también se incluyó la fuerza corporal (fuerza por unidad de volumen). La fuerza corporal representa por ejemplo la fuerza de gravedad\(B = \rho g\) o la fuerza\(B = \rho \ddot{u}\) de inercia d'Alambert para que la derivación sea válida tanto para problemas estáticos como dinámicos. Resumiendo las fuerzas se obtiene la primera ecuación de equilibrio

\[\frac{\partial \sigma_{22}}{\partial x_2} + \frac{\partial \sigma_{12}}{\partial x_1} + \frac{\partial \sigma_{32}}{\partial x_3} + B_2 = 0\]

Invocar la notación de índice

\[\frac{\partial \sigma_{j2}}{\partial x_j} + B_2 = 0 \rightarrow \sigma_{j2,j} + B_2 = 0 \label{3.1.24}\]

con la convención de suma y coma. Un procedimiento similar de suma de fuerzas puede repetirse en la\(x_3\) dirección\(x_1\) y, dando lugar a dos ecuaciones adicionales de equilibrio. Inmediatamente se puede notar que al reemplazar los subíndices de vida “2” en la Ecuación\ ref {3.1.24} respectivamente por “1” y “3”, la forma compacta final de la ecuación de equilibrio lee

\[\sigma_{ij,j} + B_i = 0 \text{ or } \frac{\partial \sigma_{ij}}{\partial x_j} + B_i = 0\]

En la notación expandida y reemplazando\(x_i\) por\((x, y, z)\), la forma familiar de la ecuación de equilibrio es

\[\color{red}{\frac{\partial \sigma_{x x}}{\partial x} + \frac{\partial \sigma_{x y}}{\partial y}} \color{black}{+ \frac{\partial \sigma_{x z}}{\partial z} + B_{x}=0}\]
\[\color{red}{\frac{\partial \sigma_{y x}}{\partial x} + \frac{\partial \sigma_{y y}}{\partial y}} \color{black}{+ \frac{\partial \sigma_{y z}}{\partial z} + B_{y}=0}\]
\[\frac{\partial \sigma_{z x}}{\partial x} + \frac{\partial \sigma_{z y}}{\partial y} + \frac{\partial \sigma_{z z}}{\partial z} + B_{z}=0\]

El caso de tensión plana, que prevalece en placas delgadas y carcasas se define por

\[\sigma_{3j} = 0 \text{ or } \sigma_{31} = \sigma_{32} = \sigma_{33} = 0\]

En otras palabras, todos los componentes del tensor de tensión que señalan en las direcciones z son cero,\(\sigma_{zz} = \sigma_{zx} = \sigma_{zy} = 0\). Los componentes del tensor de tensión plana son resaltados por el área enmarcada, por lo tanto\(\boldsymbol{\sigma}\) es igual a

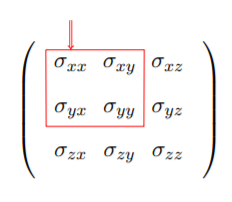
Para el estrés plano, los subíndices se ejecutan solo sobre dos dimensiones y las letras griegas se utilizan comúnmente,\(\alpha , \beta = 1, 2\). En la notación compacta, la ecuación de equilibrio de tensión plana dice

\[\sigma_{\alpha \beta, \beta} + B_{\alpha} = 0\]

En el caso uniaxial solo sobrevive un componente del equilibrio, dando

\[\frac{d \sigma_{xx}}{dx} + B = 0 \label{3.1.31}\]

Sin fuerza corporal,\(B = 0\), Ecuación\ ref {3.1.31} predice una tensión constante a lo largo de la longitud de la barra. La adición de la fuerza de inercia d'Alambert conducirá a la ecuación de onda unidimensional.