2.2: Tema Avanzado - Equilibrio Local desde el Principio del Trabajo Virtual
- Page ID
- 85244
La derivación de la ecuación local de equilibrio a partir del principio global del trabajo virtual es un método elegante en mecánica continua y estructural. Este procedimiento también formula la condición de límite estática y cinemática. Hay dos herramientas matemáticas involucradas. Uno es el teorema de la divergencia (identidad Gauss-Green) y el otro es el concepto del cálculo de variación.
El teorema de Gauss transforma la integral de volumen en una integral de superficie
\[\int_{V} A_{i,i}dV = \int_{S} A_in_idS, \; A_{i,i} = \frac{\partial A_i}{\partial x_i} \label{2.2.1}\]
donde\(A_i\) es un vector y ni es el vector normal unitario del elemento de superficie\(d\boldsymbol{S}\). En el caso unidimensional más simple, la Ecuación\ ref {2.2.1} se reduce a
\[\int_{x_1}^{x_2} \frac{dA}{dx} dx = A|_{x_1}^{x_2} = A(x_2) − A(x_1)\]
Partiendo de la definición de la deformación infinitesimal dada por la Ecuación (2.1.22), los incrementos del tensor de deformación y el vector de desplazamiento también están relacionados linealmente
\[\delta \epsilon_{ij} = \frac{1}{2} (\delta u_{i,j} + \delta u_{j,i}) \label{2.2.3}\]
Hay una fina diferencia entre el símbolo\(\delta u\) y\(du\), lo cual se explica en la Figura (\(\PageIndex{1}\)).
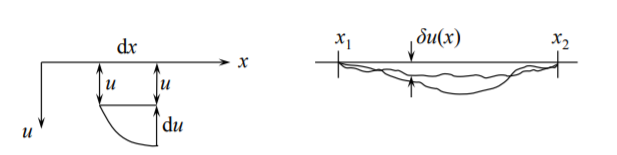
Ambos son operadores lineales y la regla para las diferenciaciones es la misma.
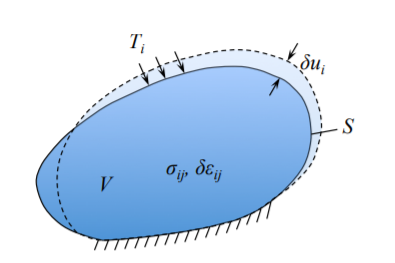
El principio del trabajo virtual establece que el trabajo incremental de tensiones sobre las tensiones sobre el volumen del cuerpo debe ser igual al trabajo de las tracciones superficiales en los desplazamientos incrementales sobre la superficie del cuerpo. La figura (\(\PageIndex{2}\)) ayuda a visualizar la notación.
Una parte de la superficie sobre la que el desplazamiento\(\delta u_i = 0\) es cero se denota por\(S_\mathrm{U}\). El resto de la superficie\(S − S_\mathrm{U}\) se denota por\(S_\mathrm{T}\). Matemáticamente el principio de los estados de trabajo virtual
\[\int_{V} \sigma_{ij}\delta \epsilon_{ij}dV = \int_{S} T_i\delta u_idS \label{2.2.4}\]
donde\(\delta \epsilon_{ij}\) se calculan a partir del\(\delta u_i\) uso de la Ecuación\ ref {2.2.3}. La interpretación gráfica unidimensional del principio se muestra en la Figura (\(\PageIndex{3}\)).
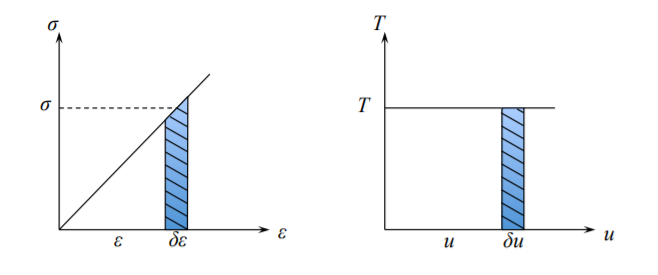
El integrando del lado izquierdo de la ecuación\ ref {2.2.4} se puede transformar a una forma más simple usando la propiedad de simetría del tensor de tensión\(\sigma_{ij} = \sigma_{ji}\)
\[\frac{1}{2}\sigma_{ij} \delta u_{i,j} + \frac{1}{2}\sigma_{ji}\delta u_{j,i} = \sigma_{ij} \delta u_{i,j} \]
Recordar una regla elemental de diferenciación del producto de dos funciones
\[(ab)^{\prime} = a^{\prime} b + ab^{\prime}\]
que en aplicación a nuestro problema lee
\[\sigma_{ij} (\delta u_{i})_{,j} = (\sigma_{ij}\delta u_{i})_{,j} - (\sigma_{ij})_{,j} \delta u_{i} \label{2.2.7}\]
Ahora, el lado izquierdo de la Ecuación\ ref {2.2.4} se transforma en
\[\int_{V} \sigma_{ij}\delta \epsilon_{ij}dV = \int_{V} \underbrace{(\sigma_{ij}\delta u_i)}_{A_i} \left._{,j} \right. dV - \int_{V} (\sigma_{ij})_{,j}\delta u_i dV \]
La primera integral de volumen se transforma ahora en la integral de superficie de acuerdo con la Ecuación\ ref {2.2.1}. Sustituyendo este resultado en la declaración de trabajo virtual se obtiene
\[\int_{S} \sigma_{ij}\delta u_i n_j dS - \int_{V} \sigma_{ij,j}\delta u_i dV = \int_{S} T_i \delta u_i dS\]
Combinando las dos integrales superficiales en una integral, finalmente llegamos
\[\int_{S} (\sigma_{ij} n_i - T_i) \delta u_i dS - \int_{V} \sigma_{ij,j}\delta u_i dV = 0\]
La primera integral se desvanece cuando
\[\sigma_{ij} n_i - T_i = 0 \text{ on } S_{\mathrm{T}}\]
\[\text{or } \delta u_i = 0 \text{ on } S_{\mathrm{U}}\]
Las ecuaciones anteriores representan respectivamente la condición de límite de esfuerzo y desplazamiento. El significado de segunda integral debe interpretarse en el espíritu del primer lema del cálculo de variación. El incremento del vector de desplazamiento no\(\delta u_i\) puede desvanecerse sobre todo el volumen del cuerpo porque esto significaría un movimiento corporal rígido. El punto es que la segunda integral en la Ecuación\ ref {2.2.7} debe ser cero no para una forma particular de\(\delta u_i\) sino para todas las posibles variaciones del campo de desplazamiento, como se muestra en la Figura (\(\PageIndex{1}\)). Así, el cálculo de la variación nos dice que esto es posible sólo cuando
\[\sigma_{ij,j} = 0 \text{ in } V \label{2.2.13}\]
El principio del trabajo virtual a menudo se llama la declaración débil (global) de equilibrio mientras que la Ecuación\ ref {2.2.13} es la ecuación local de equilibrio pero no se llama fuerte. La débil declaración de equilibrio es un punto de partida para desarrollar métodos más aproximados en mecánica continua y estructural como la expansión de valores propios, la diferencia finita o el método de elementos finitos. El supuesto crítico del primer lema del cálculo de variación es que se considera una infinidad de diferentes velocidades virtuales. Esto se logra considerando un grado de libertad grande pero finito a través de muchos términos en la expansión de valores propios o muchos elementos discretos. A través de este supuesto se logra la equivalencia de la formulación global y local.
Una forma alternativa del principio del trabajo virtual, extensamente en la teoría de la plasticidad, es el principio de velocidad virtual. Al observar que
\[\delta u = \frac{du}{dt}\delta t = \dot{u} \delta t\]
La ecuación\ ref {2.2.4} se transforma en
\[\int_{V} \sigma_{ij} \dot{\epsilon_{ij}} dV = \int_{S} T_i \dot{u_i} dS \]
donde\(\dot{\epsilon_{ij}}\) es el campo de velocidad instantánea obtenido de las velocidades incrementales\(\dot{u_i}\) a través de la relación geométrica lineal, Ecuación\ ref {2.2.4}.
Tensiones Generalizadas
Este concepto se introduce con el fin de reducir el problema bidimensional en\(x\) y\(z\) en haces a un problema unidimensional en\(x\), gobernado por una ecuación diferencial ordinaria.
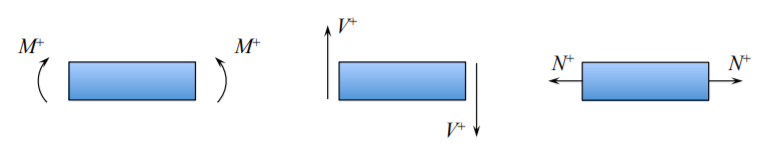
En una sección transversal arbitraria en una viga se puede distinguir un vector de momentos de flexión\(\{M_x, M_y, T\}\) donde\(M_x\) está doblando la viga en el\((x, z)\) plano,\(M_y\) y\(T\) es el par. (No confunda el par con el vector de tracción superficial). El significado del vector momento se explica en la Figura (\(\PageIndex{4}\)).
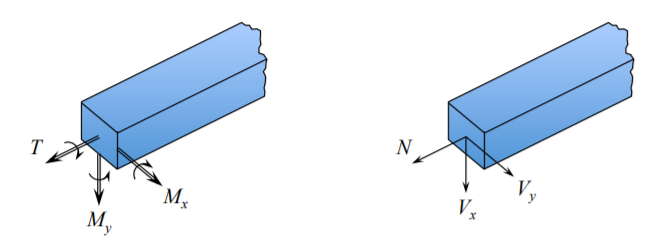
Estos son componentes del vector de momento de flexión. Los componentes del vector de fuerza que actúan en una sección transversal arbitraria\(\{V_x, V_y, N\}\) son la fuerza axial (membrana). En flexión plana de una viga solo tres de los seis componentes del estrés generalizado resultan supervivencia. Se definen por
\[M_x = M \buildrel \rm {def} \over{=} \int_{A} \sigma_{xx}z \, dA \; [\mathrm{Nm}]\]
\[N \buildrel \rm {def} \over{=} \int_{A} \sigma_{xx} \, dA \; [\mathrm{N}]\]
\[V_x = V \buildrel \rm {def} \over{=} \int_{A} \sigma_{\mathrm{xz}} \, dA \; [\mathrm{N}]\]
El producto\(\sigma_{xx}{dA}\) en la Ecuación (3.36a) es la fuerza incremental. Multiplicar esta fuerza por el “brazo”\(z\) desde el eje de flexión de la viga da el momento de delimitación incremental\(dM = (\sigma_{xx}dA)z\). El momento de flexión total es una integral de la\(dM\) sección transversal de la viga. El signo de las cantidades generalizadas se decide por el signo del estrés.
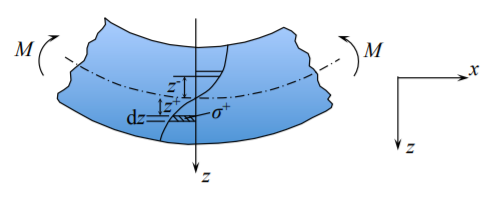
Imagínese que la viga está doblada de la manera que se muestra en la Figura (\(\PageIndex{5}\)). En el lado de tracción de la viga la tensión es positiva,\(\sigma^+\) y también lo es la distancia desde el eje de la viga. En el lado compresivo tanto los brazos de tensión como los de fuerza son negativos\(\sigma^-z^-\), pero el producto es positivo. Por lo tanto, el lado de tracción y compresión de la viga contribuyen al momento de flexión positivo. La viga (o su porción) donde el momento de flexión es negativo se llama “viga sonriente”. Por lo tanto, al observar la forma deformada de la viga se puede determinar inmediatamente el signo del momento de flexión. El signo de la fuerza axial y de cizallamiento se puede determinar fácilmente a partir de la Figura (\(\PageIndex{6}\)).