2.4: Tema Avanzado - Principio de Trabajo Virtual para Vigas

Este principio puede derivarse directamente del principio general 3-D, Ecuación (2.2.3) asumiendo el estado de tensión unidimensional y la suposición cinemática de la teoría del haz elemental

\ [\ begin {array}
\ sigma_ {ij}\ fila derecha\ sigma_ {xx}\\ delta
\ epsilon_ {ij}\ fila derecha\ delta\ epsilon_ {xx} =\ delta\ épsilon^ {\ circ} (x) + z\ delta\ kappa\ texto {de la Ecuación} (1.5.15)\
dV = dA dx,\; 0<x<l
\ end {array}\]

El lado izquierdo (LH) de la Ecuación (2.2.4) se convierte en

\[\mathrm{LH} = \int_{V} \sigma_{ij}\delta \epsilon_{ij}dV = \int_{0}^{l} \left\{ \int_{A} [\sigma_{xx}\delta \epsilon^{\circ}(x)dA + \sigma_{xx} z \delta \kappa dA] \right\} dx \]

Ambos\(\delta\epsilon^{\circ}(x)\) y\(\delta \kappa (x)\) son extensión y curvatura del eje de la viga y son constantes con respecto a la integración sobre el área. La ecuación anterior se puede simplificar aún más

\[\mathrm{LH} = \int_{0}^{l} \left[ \delta\epsilon^{\circ}(x) \int_{A} \sigma_{xx} dA + \delta \kappa (x) \int_{A} \sigma_{xx} z dA \right] dx\]

Recordando la definición de la fuerza axial, Ecuación (2.2.17) y el momento de flexión, Ecuación (2.2.16), la expresión final para la obra virtual dentro del volumen de la viga toma esta forma simple

\[\mathrm{LH} = \int_{0}^{l} (N \delta\epsilon^{\circ} + M\delta \kappa) dx\]

donde\(l\) es la longitud de la viga. La evaluación del lado derecho (RH) de la Ecuación (2.2.4) es más interesante.

Figura\(\PageIndex{1}\): La superficie exterior de la viga consta de dos partes: la superficie lateral\(S_L\) sobre la que está actuando la tracción superficial y los cortes finales\(A\).

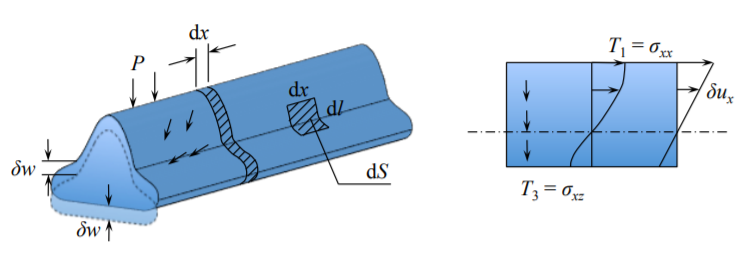
Tenga en cuenta que todos los puntos de una porción de la viga se mueven hacia abajo con el desplazamiento virtual\(\delta w\). Los cortes finales se trasladan y giran, de acuerdo con la Ecuación (1.5.1). Entonces el lado derecho de la Ecuación (2.2.4) se convierte en

\[\mathrm{RH} = \int_{0}^{l} q\delta w dx + \int_{A} \sigma_{xx} [\delta u^{\circ} - \delta \theta z] dA + \int_{A} \sigma_{xz} \delta w dA \label{2.4.5}\]

donde\(q\) está la presión integrada sobre la circunferencia de una rebanada

\[q = \oint T_iV_i ds \label{2.4.6}\]

y\(V_i\) son coseno de dirección del vector de tracción superficial con respecto al\(z\) eje. En el caso de la sección rectangular\((h \times b)\), la Ecuación\ ref {2.4.6} reduce a

\[q = pb\]

donde\(p\) se encuentra la presión distribuida en el lado superior de la viga y\(q\) se llama carga de línea. El segundo término en la Ecuación\ ref {2.4.5} puede simplificarse usando las definiciones Ecuaciones (2.2.16-2.2.18)

\[\bar{M} = \int_{A_{\text{end}}} \sigma_{xx} z dA \]

\[\bar{N} = \int_{A_{\text{end}}} \sigma_{xx} dA \]

\[\bar{V} = \int_{A_{\text{end}}} \sigma_{xz} dz\]

donde la barra sobre el símbolo indica que este es el valor al final de la viga. La expresión final del principio de trabajo virtual para una viga toma la forma

\[\int_{0}^{l} \left(N \delta \epsilon^{\circ} + M \delta \kappa\right) d x = \int_{0}^{l} q(x) \delta w d x + \bar{N} \delta u^{\circ} - \bar{M} \delta \theta + \bar{V} \delta w\]

El principio anterior se utilizará para derivar soluciones aproximadas de los problemas del haz y también para obtener las ecuaciones de equilibrio y condiciones límite.