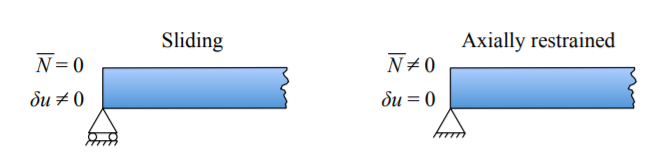2.5: Derivación de la Ecuación de Equilibrio para Vigas a partir del Principio de Trabajo Virtual
- Page ID
- 85231
El aparato matemático necesario es la integración por partes. El punto de partida en la Ecuación (2.2.6) que se pone en una forma alternativa
\[\frac{da}{dx}b = \frac{d}{dx} (ab) - a\frac{db}{dx}\]
Integrando ambos lados de la ecuación anterior en gets
\[\int \frac{da}{dx}bdx = ab|_{\text{ends}} - \int a\frac{db}{dx} dx\]
Para simplificar la notación se utilizará la convención “prime” a lo largo de
\[\frac{d[]}{dx} = {[]}^{\prime}; \; \frac{d^2 []}{dx^2} = {[]}^{\prime\prime}\]
Giramos ahora el lado izquierdo del principio de trabajo virtual, Ecuación (2.1.22) y recordamos la definición de curvatura del haz y deformación axial
\[\kappa = -w^{\prime\prime}\]
\[\epsilon^{\circ} = u^{\prime}\]
Los incrementos virtuales son
\[\delta\kappa = -\delta w^{\prime\prime} = (\delta w^{\prime})^{\prime}\]
\[\delta\epsilon^{\circ} = \delta u^{\prime} \label{2.5.7}\]
Sustituyendo la Ecuación\ ref {2.5.7} en el lado LH de la Ecuación (2.1.22) e integrando dos veces por partes obtenemos
\[\begin{align} \mathrm{LH} &= - \int_{0}^{l} M (\delta w^{\prime})^{\prime} dx + \int_{0}^{l} N \delta u^{\prime} dx \\[4pt] &= - \left( M \delta w^{\prime} |_{0}^{l} - \int_{0}^{l} M^{\prime} \delta w^{\prime} dx \right) + \left( N \delta u |_{0}^{l} - \int_{0}^{l} N \delta u dx \right) \\[4pt] &= - M \delta w^{\prime} |_{0}^{l} + M^{\prime} \delta w |_{0}^{l} - \int_{0}^{l} M^{\prime\prime} \delta w dx + N\delta u |_{0}^{l} - \int_{0}^{l} N^{\prime} \delta u dx \label{2.5.8} \end{align}\]
El segundo término representa el incremento de trabajo en el extremo de la viga en desplazamiento virtual descendente. Por lo tanto, la fuerza generalizada correspondiente debe ser la fuerza cortante\(V\)
\[V = M^{\prime}\]
Introduciendo la ecuación\ ref {2.5.8} en la ecuación (2.4.11) y agrupando los términos rinde
\[\int_{0}^{l} (M^{\prime\prime} + q)\delta w dx + \int_{0}^{l} N^{\prime} \delta u dx + (M - \bar{M}) \delta w^{\prime} |_{0}^{l} - (N - \bar{N}) \delta u |_{0}^{l} - (V - \bar{V}) \delta w |_{0}^{l} = 0\]
La ecuación anterior no debe sostenerse para un desplazamiento incremental específico sino para variaciones arbitrarias\((\delta w, \delta w^{\prime}, \delta u)\), independientes dentro\(0 < x < l\) y en los límites. Por lo tanto, por el primer lema del cálculo de variación, sigue la forma local (fuerte) del equilibrio del haz
\[M^{\prime\prime} + q = 0\]
\[N^{\prime} = 0\]
junto con las condiciones de contorno
\[ (M - \bar{M}) \delta w^{\prime} = 0 \]
\[ (V - \bar{V}) \delta u = 0\]
\[ (N - \bar{N}) \delta w = 0\]
Con el fin de satisfacer la condición de límite
\[\text{either } M = \bar{M} \text{ or } \delta w^{\prime} = 0 \label{2.5.16}\]
\[\text{either } V = \bar{V} \text{ or } \delta w = 0 \label{2.5.17}\]
\[\text{either } N = \bar{N} \text{ or } \delta u = 0 \label{2.5.18}\]
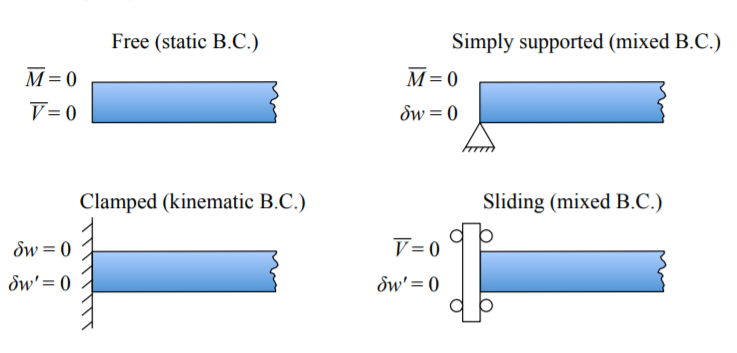
Las cantidades con una barra denota las cantidades prescritas en los extremos de una viga. En particular\(\bar{M}\),\(\bar{V}\), y\(\bar{N}\) podría ser igual a cero. La primera columna en Ecuaciones\ ref {2.5.16} -\ ref {2.5.18} representa las condiciones de límite estáticas mientras que la segunda columna las condiciones de contorno cinemáticas. También hay condiciones de límite mixtas. Las siguientes combinaciones satisfacen todas las condiciones de contorno, Figura (\(\PageIndex{1}\)).
Además la viga podría deslizarse libremente en el extremo a lo largo del eje x o se puede evitar que se deslice, Figura (\(\PageIndex{2}\)).
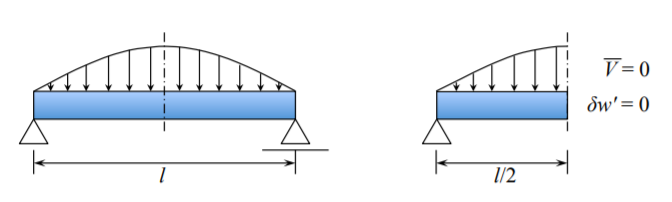
En el caso de carga simétrica de la viga, basta con considerar solo la mitad de la viga con la condición de límite de simetría. La simetría B.C. es idéntica a las condiciones de contorno deslizante, como se explica en la Figura (\(\PageIndex{3}\)).