4.1: Ecuaciones gobernantes
- Page ID
- 85144
Hasta el momento hemos establecido tres grupos de ecuaciones que caracterizan completamente la respuesta de los haces a diferentes tipos de carga. En el Capítulo 1 se establecieron relaciones para calcular las cepas a partir del campo de desplazamiento.
\[\epsilon(x, z) = \epsilon^{\circ}(x) + z\kappa\]
donde
\[\epsilon^{\circ}(x) = \frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2 \; , \; \kappa = −\frac{d^2w}{dx^2} \label{4.1.2}\]
Las relaciones geométricas anteriores son independientes del equilibrio y se aplican a cualquier tipo de materiales.
El segundo conjunto de ecuaciones, derivado en el Capítulo 2, es el requisito de equilibrio
\[\frac{dV^*}{dx} + q(x) = 0 \quad − \quad \text{ force equilibrium}\]
\[\frac{dM}{dx} - V = 0 \quad − \quad \text{ moment equilibrium} \label{4.1.4}\]
donde\(V^* = V + N \frac{dw}{dx}\) está el cizallamiento efectivo.
\[\frac{dN}{dx} = 0 \]
Eliminando\(V\) y\(V^*\) entre las ecuaciones anteriores, se obtuvo la ecuación de equilibrio del haz (Ver Ecuación (2.7.1))
\[\frac{d^2M}{dx^2} + N\frac{d^2w}{dx^2} + q = 0 \label{4.1.7}\]
La derivación del equilibrio es válida para todo tipo de materiales. En la teoría de las deflexiones moderadamente grandes, el equilibrio se acopla con la cinemática.
El tercer grupo de ecuaciones define el comportamiento material y relaciona las tensiones generalizadas con las fuerzas generalizadas
\[N = EA\epsilon^{\circ} \label{4.1.8}\]
\[M = EI\kappa \label{4.1.9}\]
La independencia de la geometría y el equilibrio sobre la ecuación constitutiva permite desarrollar el marco general de un solucionador en los códigos de Elementos Finitos. Las ecuaciones constitutivas se pueden agregar como subrutinas definidas por el usuario.
Consideremos primero las deformaciones infinitesimales (pequeñas rotaciones para las cuales el término\(\frac{1}{2} \left( \frac{dw}{dx} \right)^2\) desaparece en la Ecuación\ ref {4.1.2} y el término\(\frac{d^2w}{dx^2} = 0\) en la Ecuación\ ref {4.1.7}. Luego de Ecuaciones\ ref {4.1.2},\ ref {4.1.4} y\ ref {4.1.8} se obtiene
\[EA\frac{d^2u}{dx^2} = 0\]
Eliminando los momentos de curvatura y flexión entre las ecuaciones\ ref {4.1.2},\ ref {4.1.7} y\ ref {4.1.9}, se obtiene la ecuación de deflexión del haz
\[EI\frac{d^4w}{dx^4} = q(x) \label{4.1.11}\]
La carga concentrada\(P\) puede tratarse como un caso especial de la carga distribuida\(q(x) = P \delta(x − x_0)\), donde\(\delta\) se encuentra la función delta Dirac.
Consideremos primero la Ecuación\ ref {4.1.4} para el desplazamiento axial. Las condiciones de contorno en la\(x\) dirección -son
\[(N − \bar{N})\delta u = 0\]
La solución general para\(u(x)\) es
\[\frac{du}{dx} = D_1 \; , \; u = D_1x + D_0 \label{4.1.13}\]
Hay dos constantes de integración y se necesitan dos condiciones de límite. Solo hay cuatro combinaciones de condiciones de contorno:
1. Viga restringida al movimiento axial, ver Figura (\(\PageIndex{1}\)).
\[u(x = 0) = u(x = l) = 0\]
Esto da lugar a la solución de dos ecuaciones algebraicas
\[0 = D_0 + D_1 \cdot 0\]
\[0 = D_0 + D_1l\]
que da\(D_0 = D_1 = 0\) y\(u(x) = 0\). Se trata de un caso trivial, para el cual la fuerza axial también se\(N = EA\frac{du}{dx}\) desvanece.
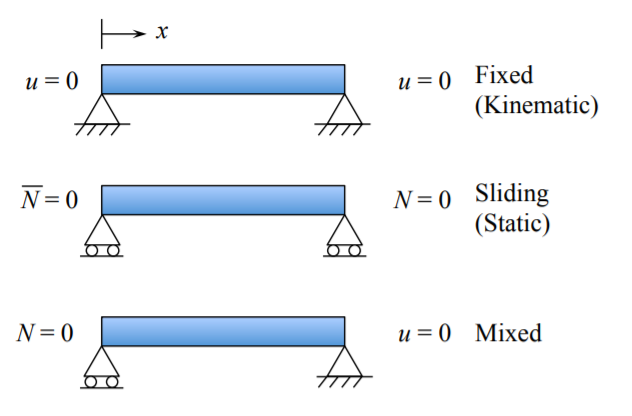
2. Se permite que la viga se deslice en la\(x\) dirección -en ambos extremos.
\[\bar{N} = N = 0 \text{ at } x = 0 \text{ and } x = l\]
La fuerza axial es proporcional a\(\frac{du}{dx}\). De la Ecuación\ ref {4.1.13} podemos ver que el gradiente de\(u\) es cero a lo largo de toda la viga. Entonces, si\(\bar{N} = 0\) o\(\frac{du}{dx}\) desaparece en un extremo, digamos\(x = 0\),\(D_1 = 0\) y automáticamente\(\bar{N} = 0\) se satisface en el otro extremo,\(x = l\). La constante de integración\(D_0\) es indeterminada, lo que significa que se permite la traslación del cuerpo rígido de toda la viga.
3. Para evitar la traslación del cuerpo rígido, un extremo de la viga, digamos\(x = 0\), debe fijarse contra el movimiento en la\(x\) dirección -dirección. Por lo tanto
\[\bar{N} = 0 \text{ or } \frac{du}{dx} = 0 \quad \text{ at } \quad x = 0\]
\[u = 0 \quad \text{ at } \quad x = l\]
que son precisamente las condiciones límite para el tercer caso. De la ecuación\ ref {4.1.13} obtenemos
\[D_1 = 0\]
\[D_1l + D_2 = 0 \rightarrow D_2 = 0 \]
Ahora, el desplazamiento axial desaparece,\(u(x) = 0\) pero se elimina la traslación del cuerpo rígido.
Para los tres casos anteriores de condiciones cinemáticas estáticas y de límite mixto, la fuerza axial fue cero.
4. Si un extremo de la viga (barra) es cargado por una fuerza dada\(\bar{N}\) y el otro es fijo, las condiciones de contorno (BC) son
\[\begin{array}{lcl} N = -\bar{N} \; , \; EA\frac{du}{dx} = 0 & \text{ at } x = 0 \\ u = 0 & \text{ at } x = l \end {array}\]
\[D_1 = − \frac{\bar{N}}{EA} \; , \; D_2 = \frac{\bar{N}l}{EA}\]
y la solución es
\[u(x) = \frac{\bar{N}}{EA} (l − x)\]
El caso en el que se retiene el término no lineal en la Ecuación\ ref {4.1.2} es mucho más interesante. Esto se tratará en la sección sobre deflexión moderadamente grande de vigas.
Ahora volvemos nuestra atención a la solución de la desviación del haz, Ecuación\ ref {4.1.11}. Esta es la ecuación lineal no homogénea de cuarto orden que requiere cuatro condiciones de límite. Hay cuatro tipos de condiciones de contorno, definidas por
\[(M − \bar{M})\delta w^{\prime} = 0\]
\[(V − \bar{V}) \delta w = 0\]
En aras de la ilustración, seleccionamos un pasador BC para una viga cargada por la carga similar uniforme\(q\), Figura (\(\PageIndex{2}\)).
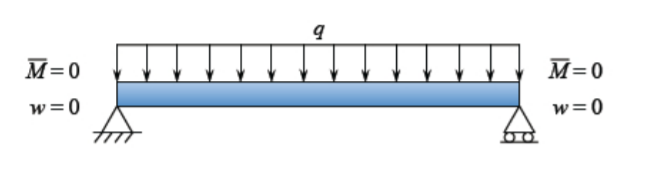
El momento de flexión es proporcional a la curvatura. La ecuación\ ref {4.1.11} se somete entonces a las siguientes condiciones de límite:
\[w(x = 0) = w(x = l) = 0\]
\[\left. \frac{d^2w}{dx^2}\right|_{x=0} = \left. \frac{d^2w}{dx^2} \right|_{x=l} = 0 \]
Integremos la ecuación diferencial cuatro veces con respecto a\(x\):
\[\begin{align} \frac{d^3w}{dx^3} &= \frac{qx}{EA} + C_1 \\[4pt] \frac{d^2w}{dx^2} &= \frac{qx^2}{EA2} + C_1x + C_2 \\[4pt] \frac{dw}{dx} &= \frac{qx^3}{EA6} + \frac{C_1x^2}{2} + C_2x + C_3 \\[4pt] w &= \frac{qx^4}{EA24} + \frac{C_1x^3}{6} + \frac{C_2x^2}{2} + C_3x + C_4 \end{align}\]
Sustituyendo el BC en las soluciones generales, se obtiene
\[0 = C_2\]
\[0 = \frac{ql^3}{2EA} + {C_1}l + C_2 \]
\[0 = C_4\]
\[0 = \frac{ql^4}{24EA} + \frac{C_1l^3}{6} + \frac{C_2l^2}{2} + C_3l + C_4 \]
La solución del sistema anterior es
\[C_1 = −\frac{ql}{2}\]
\[C_2 = 0\]
\[C_3 = \frac{ql^3}{12}\]
\[C_4 = 0\]
La relación carga-desplazamiento se convierte
\[w(x) = \frac{qx}{24EA}(l^3 - 2lx^2 + x^3) \label{4.1.40}\]
Ecuación diferenciadora\ ref {4.1.40} dos veces, la expresión para el momento de flexión es
\[M(x) = \frac{qx}{2} (l − x)\]
y diferenciando de nuevo, la fuerza de corte se convierte en
\[V(x) = \frac{dM}{dx} = \frac{q}{2} (l − 2x)\]
Las gráficas de los momentos de flexión normalizados y las fuerzas de cizallamiento se muestran en la Figura (\(\PageIndex{3}\)).
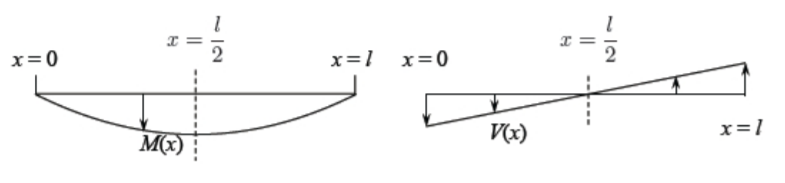
\(V = EI\frac{d^3w}{dx^3}\)Se ve que la fuerza cortante desaparece en la mitad del tramo de la viga. También la pendiente\(\frac{dw}{dx}\) es cero en esta ubicación. Hemos demostrado que en el plano de simetría
\[V (x = \frac{l}{2} ) = 0 \label{4.1.43}\]
\[\left. \frac{dw}{dx}\right|_{x= \frac{l}{2}} = 0 \label{4.1.44}\]
Inversamente, si el problema es simétrico, que las Ecuaciones\ ref {4.1.43} -\ ref {4.1.44} deben mantenerse en el plano de simetría. Como formulación alternativa, se puede considerar la mitad del haz con la simetría BC.
¿Se puede resolver el problema anterior y compararlo con solución de la viga pin pin, Ecuación\ ref {4.1.40}?
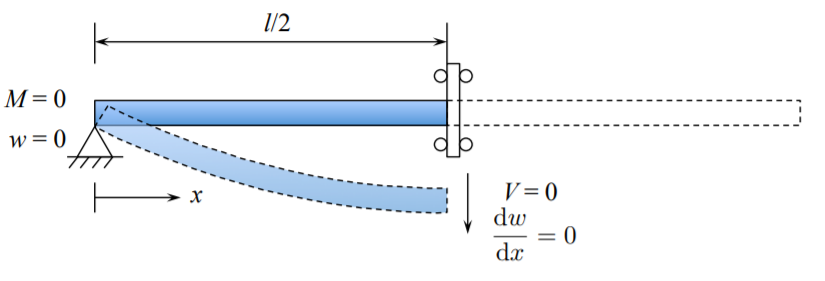
Cabe mencionar que la viga soportada pin pin es una estructura estáticamente determinada. Por lo tanto, la distribución de las fuerzas de corte y los momentos de flexión se puede determinar a partir de la ecuación de equilibrio ¿Puedes hacerlo y obtener correctamente las señales?
El propósito del Capítulo 4 es presentar propiedades de las ecuaciones y soluciones gobernantes. los estudiantes interesados son referidos al capítulo final de conjuntos de problemas donde se consideran muchas vigas con diferente carga y BC. También el libro de referencia recomendado y las monografías presentan solución a algunos problemas de haz comunes.


