4.2: Propiedades Generales de la Ecuación Gobernante del Haz- Soluciones Generales y Particulares
- Page ID
- 85151
Recordemos del Cálculo que la solución de la ecuación diferencial ordinaria lineal no homogénea es una suma de la solución general de la ecuación homogénea\(w_g\) y la solución particular de la ecuación no homogénea\(w_p\). La propiedad de homogeneidad significa que\(f(Ax) = Af(x)\). La contraparte homogénea de la Ecuación (4.1.11) es
\[EI \frac{d^4w}{dx^4} = 0 \quad \text{ or } \quad \frac{d^4w}{dx^4} = 0 \label{4.2.1}\]
y su solución, obtenida por cuatro integraciones es el polinomio de tercer orden
\[w_g(x) = \frac{C_1x^3}{6} + \frac{C_2x^2}{2} + C_3x + C_4 \label{4.2.2}\]
La solución particular\(w_p\) de la ecuación de deflexión del haz, Ecuación (4.1.11) depende de la carga, pero no de las condiciones límite. Para el haz uniformemente cargado la solución particular es el primer término en la Ecuación (4.1.27-4.1.28). Como ilustración, considere la misma viga soportada por pasador y pasador cargada por la carga de línea triangular
\[q(x) = q_0 \frac{2x}{l} \; , \; 0 < x < \frac{l}{2}\]
donde\(q_0\) es la intensidad de carga a mitad de lapso\(x = l/2\). La solución particular de este problema, satisfaciendo la ecuación gobernante es
\[w_p = \frac{q_0x^5}{60EIl}\]
Entonces, la solución completa es\(w(x) = w_g + w_p\).
La viga cargada por fuerzas concentradas (o momentos) requiere una consideración especial.
Requisitos de continuidad
Un cambio repentino en la sección transversal o carga de la viga puede producir una solución discontinua. ¿Qué cantidades pueden sufrir un salto y qué debe ser continuo?

En mecánica la discontinuidad de una función dada se denota con un corchete
\[[f(\xi)] = f(\xi^+) − f(\xi^-)\]
donde\(\xi^+\) y\(\xi^-\) denotan los valores del argumento en la mano derecha e izquierda de una discontinuidad. En la teoría cuasi-estática del haz
\[[w] = 0 \label{4.2.6}\]
\[\left[\frac{dw}{dx}\right] = 0\]
La discontinuidad en el desplazamiento vertical significa separación por lo que, por supuesto, puede que no ocurra. ¿Por qué entonces las pendientes deben ser continuas para las vigas elásticas? Esto es sencillo. Un cambio de pendiente se llama curvatura. Un salto en la pendiente da una curvatura infinita, y así un infinito momentos de flexión. Tal situación es imposible, porque la sección transversal de la viga entrará en rango de plástico, y la viga ya no permanecerá elástica. Las cantidades que pueden ser discontinuas son
\[\text{Bending monents } \quad [M] = \bar{M} \]
\[\text{Shear force } \quad [V] = \bar{V} \label{4.2.9}\]
Como ilustración, considere una viga soportada por pasador y pasador cargada a mitad de tramo por una fuerza puntual\(P\).
Como se mencionó anteriormente, la carga puntual puede considerarse como un caso limitante de una carga de línea continua con la ayuda de la función delta Dirac
\[q(x) = P \delta(x − \frac{l}{2}), \quad \text{ where } \int \delta(x − \frac{l}{2})dx = 1 \]
A pesar de que se han desarrollado técnicas para tratar las funciones de singularidad de los haces, requieren utilizar el aparato de la teoría matemática de la distribución. Este
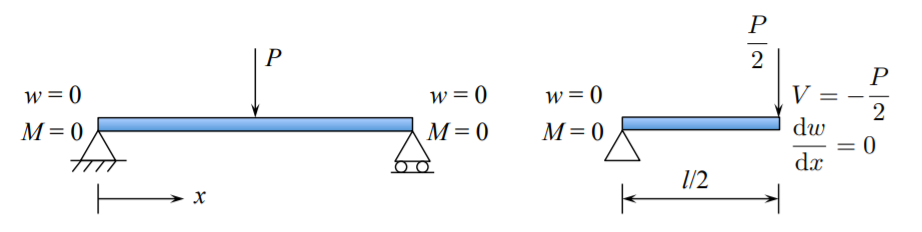
no es la avenida que tomaremos. En cambio, se impondrá una condición de límite de simetría. Ahora, la carga concentrada no se aplica dentro de la viga\(0 < x < l\), gobernada por la ecuación diferencial no homogénea, sino en el límite. Cada mitad de la viga lleva la mitad de la carga. Por lo tanto, las condiciones de contorno son
\[\text { at } x = 0 \; w = 0 \]
\[ \frac{d^{2} w}{d x^{2}} = 0\]
\[\text { at } x = \frac{l}{2} \; V= -\frac{P}{2} \]
\[ \frac{d w}{d x} = 0\]
Debido a que la carga se aplica en el límite, la ecuación diferencial se vuelve homogénea. La solución de la Ecuación\ ref {4.2.1} viene dada por el polinomio de tercer orden, sustituyendo el BC anterior en la solución dada por la Ecuación\ ref {4.2.2}, se obtiene un sistema de cuatro ecuaciones algebraicas lineales, donde la solución es
\[C_1 = − \frac{D}{2EI} , \; C_2 = 0, \; C_3 = \frac{Pl^2}{16EI}, \; C_4 = 0 \]
La línea de deflexión viene dada por
\[w(x) = \frac{P x}{48EI} (3l^2 − 4x^2 )\]
y la desviación central (algo para recordar) es
\[w_0 = w(x = \frac{l}{2} ) = \frac{pl^3}{48EI}\]
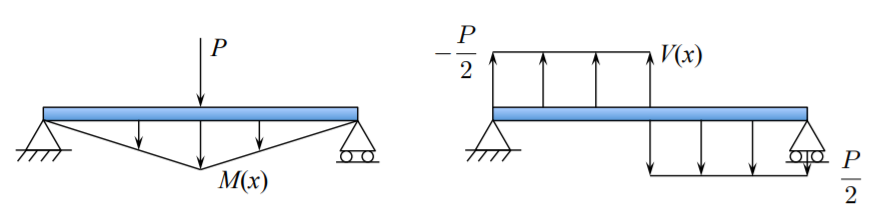
La gráfica de la distribución del momento de flexión y las fuerzas de corte a lo largo de la longitud de la viga determinada a partir de la línea de deflexión calculada se muestra en la Figura (\(\PageIndex{3}\)).
Tenga en cuenta que el salto en la fuerza de corte interna es igual a la fuerza aplicada
\[[V ] = V_{\text{right}}(x = \frac{l}{2}) − V_{\text{left}}(x = \frac{l}{2}) = P\]
Si la carga puntual no se aplica en el tramo medio sino a una distancia arbitraria\(x = a\), la viga debe dividirse en dos partes\(0 < x < a\)\(a < x < l\), y cada parte debe resolverse de forma independiente.
\[\text{First segment } 0 < x < a \; w^{\mathrm{I}}(x) = \frac{C_1x^3}{6} + \frac{C_2x^2}{2} + C_3x + C_4\]
\[\text{Second segment } a < x < l \; w^{\mathrm{II}}(x) = \frac{C_5x^3}{6} + \frac{C_6x^2}{2} + C_7x + C_8\]
Esto da lugar a ocho constantes de integración, cuatro por cada lado. ¿Habría condiciones suficientes para determinar estas constantes? La respuesta es SÍ. Hay dos condiciones de límite en\(x = 0\), cuatro condiciones de continuidad en\(x = a\), dadas por Ecuaciones\ ref {4.2.6} -\ ref {4.2.9} y, nuevamente, dos condiciones de límite en\(x = l\). En resumen
\ [\ begin {array} {l|l|l}
\ mathrm {BC}, x = 0 &\ text {Continuidad,} x = a &\ mathrm {BC}, x = l\
\ hline w = 0 & {[w] = 0} & w = 0\\
M = 0 & {\ izquierda [\ frac {d w} {d x}\ derecha] = 0} & MR =0\\
& {[M] = 0}\\
& {[V] = P}
\ fin {matriz}\]
Tenga en cuenta que no hay momento de flexión concentrado aplicado de\(\bar{M} = 0\) manera que el campo de momento de flexión es continuo a través\(x = a\). La fuerza concentrada produce un salto en la distribución de las fuerzas de corte, entonces\(\bar{V} = P\).
Dejamos al lector aplicar la condición anterior y resolver el problema. Más sobre este problema se puede encontrar en dos secciones de estas notas: Conjuntos de problemas y recitaciones.
El método de superposición dice que las deflexiones y pendientes de la viga sometida a un sistema de cargas son iguales a la suma de esas cantidades debido a cargas individuales. En otras palabras, los resultados individuales pueden superponerse para determinar una respuesta combinada, de ahí el término método de superposición.
Este es un método muy potente y conveniente ya que las soluciones para muchas condiciones de soporte y carga están fácilmente disponibles en varios manuales de ingeniería. Usando el principio de superposición, podemos combinar estas soluciones para obtener una solución para condiciones de carga más complicadas.
Como ejemplo, considere una viga sujetada cargada por una carga lineal uniforme\(q\) y una fuerza concentrada en el centro\(P\). Las fórmulas de deflexión para las dos cargas individuales son
\[w|_{\text{uniform}} = \frac{qx^2}{24EI} (l − x)^2\]
\[w|_{\text{point}} = \frac{Px^2}{48EI} (3l − 4x)\]
La solución para ambas cargas que actúan juntas es
\[w_{\text{total}} = w|_{\text{uniform}} + w|_{\text{point}}\]


