5.1: Formulación General

Última actualización
Guardar como PDF

Page ID: 85097

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Comparada con la teoría clásica de vigas con deformación infinitesimal, la teoría de deflexión moderadamente grande introduce cambios en la relación deformación-desplazamiento y equilibrio vertical, pero deja la ecuación constitutiva y el equilibrio horizontal sin cambios. La relación cinemática, Ecuación (1.9.5) adquiere ahora un nuevo término debido a rotaciones finitas del elemento viga.

\[\epsilon^{\circ} = \frac{du}{dx} + \boxed{\frac{1}{2} \left(\frac{dw}{dx}\right)^2} − \text{ new term} \label{5.1.1}\]

La definición de curvatura también tiene un término de rotación no lineal

\[\kappa = -\frac{\frac{d^2w}{dx^2}}{\left[ 1+ \left(\frac{dw}{dx}\right)^2\right]^{3/2}} \label{5.1.2}\]

El cuadrado de la pendiente puede ser grande, en comparación con el término\(\frac{du}{dx}\) y debe ser retenido en la Ecuación\ ref {5.1.1}. Al mismo tiempo los cuadrados de la pendiente (rotación de la viga) son pequeños en comparación con la unidad. ¿Por qué? Esto se explica en la Figura (\(\PageIndex{1}\)), donde se traza el cuadrado de la pendiente contra el talud.

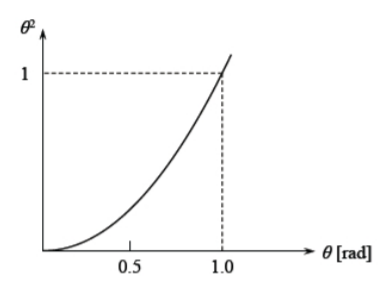
5.1.1.png — Figura\(\PageIndex{1}\): La significancia del cuadrado del término de pendiente.

A\( = 57\) grados\(\theta = 1\) rad los dos términos en el denominador de la Ecuación\ ref {5.1.2} son iguales. Sin embargo, la teoría de las deflexiones moderadamente grandes son válidas hasta\(\theta = 10^{\circ} \approx 0.175\) rad. El término\(\theta^2\) equivale a\(0.03\), que es despreciable en comparación con la unidad. Por lo tanto, la curvatura se define de la misma manera que en la teoría de las pequeñas deflexiones

\[\kappa = -\frac{d^2w}{dx^2}\]

Se demostró en el Capítulo 2 que la ecuación de equilibrio en la dirección horizontal no se ve afectada por la rotación finita. Por lo tanto, inferimos de la Ecuación (2.7.4) que la fuerza axial es constante o cero

\[N = \text{ constant}\]

El equilibrio vertical, dado por la Ecuación (3.79) tiene un nuevo término no lineal

\[\frac{d^2M}{dx^2} + \boxed{N\frac{d^2w}{dx^2}}^{-\text{new term}} +q = 0\]

Finalmente, la ley de elasticidad no se ve afectada por la rotación finita

\[N = EA\epsilon^{\circ}\]

\[M = EI\kappa\]

La solución al problema acoplado depende de las condiciones de contorno en la dirección horizontal. Refiriéndose a la Figura 4.1.1, se deben considerar dos casos:

Caso 1, viga libre para deslizarse,\(N = 0, \; u \neq 0\).
Caso 2, viga fija,\(u = 0, \; N \neq 0\).