5.2: Solución para un soporte de viga sobre rodillo

Última actualización
Guardar como PDF

Page ID: 85101

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Considerar el primer caso 1. De la ecuación constitutiva, cero haces de fuerza axial que no hay extensión del eje de la viga,\(\epsilon^{\circ} = 0\). Luego, de la Ecuación (5.1.1)

\[\frac{du}{dx} = \frac{1}{2}\left(\frac{dw}{dx}\right)^2 \label{5.2.1}\]

Al mismo tiempo, el término no lineal en el equilibrio vertical desaparece y la respuesta del haz se rige por la ecuación diferencial lineal

\[EI\frac{d^4w}{dx^4} = q(x)\]

que es idéntica a la derivada para las deflexiones infinitesimales. Como ejemplo, considere la viga soportada por pasador bajo carga de punto de tramo medio. A partir de las ecuaciones (4.3.7) y (4.3.8), el perfil de deflexión es

\[w(x) = w_o \left[ 3 \frac{x}{l} − 4\left(\frac{x}{l}\right)^3\right]\]

y la pendiente es

\[\frac{dw}{dx} = \frac{w_o}{l}\left[3 − 12\left(\frac{x}{l}\right)^2\right]\]

donde\(w_o\) está la deflexión central de la viga. Ahora, la Ecuación\ ref {5.2.1} se puede usar para calcular el desplazamiento horizontal relativo\(\Delta u\). Integrando la ecuación\ ref {5.2.1} en los límites\((0, l)\) da

\[\int_{0}^{l} \frac{du}{dx} dx= u|_{0}^{l} = u(l) − u(0) = \Delta u = − \int_{0}^{l} \frac{1}{2} \left( \frac{dw}{dx}\right)^2 dx\]

El resultado de la integración es

\[\Delta u \approx 7 \frac{w_{o}^2}{l}\]

Para obtener una idea física del resultado anterior, los desplazamientos verticales y horizontales se normalizan por el grosor\(h\) de la viga

\[\frac{\Delta u}{h} = \frac{7}{l/h} \left(\frac{w_{o}}{h}\right)^2\]

Para una viga con\(\frac{l}{h} = 21\), el resultado

\[\frac{\Delta u}{h} = \frac{1}{3} \left(\frac{w_{o}}{h}\right)^2\]

se representa en la Figura (\(\PageIndex{1}\)).

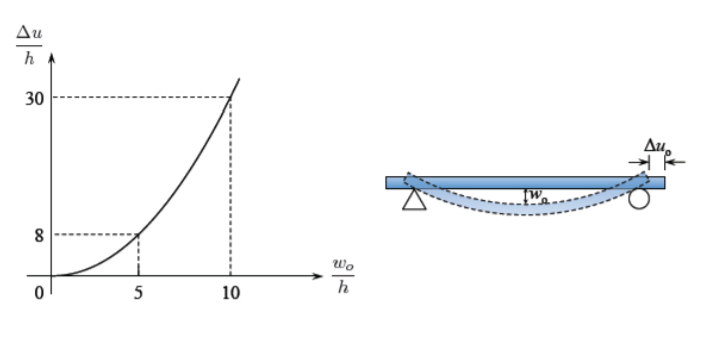
5.2.1.png — Figura\(\PageIndex{1}\): Deslizamiento de una viga desde el soporte del rodillo.

Se ve que la cantidad de deslizamiento en la dirección horizontal puede ser muy grande en comparación con el grosor.

Para resumir los resultados, la viga soportada por rodillo puede tratarse como una viga clásica aunque los desplazamientos y rotaciones sean grandes (moderados). La solución de la ecuación diferencial lineal puede entonces ser utilizada a posteriori para determinar la magnitud del deslizamiento. El análisis de la viga completamente restringida es mucho más interesante y difícil. Este es el tema de la siguiente sección.